Hull J.C. Risk management and Financial institutions
Подождите немного. Документ загружается.

Answers to Problems and Questions 447
options equals the maturity of the forward contract. If the no-default
value of the contract is positive at maturity, the call has a positive value
and the put is worth zero. The impact of defaults on the forward contract
is the same as that on the call. If the no-default value of the contract is
negative at maturity, the call has a zero value and the put has a positive
value. In this case, defaults have no effect. Again the impact of defaults
on the forward contract is the same as that on the call. It follows that the
contract has a value equal to a long position in a call that is subject to
default risk and short position in a default-free put.
12.10. Suppose that the forward contract provides a payoff at time T.
With our usual notation, the value of a long forward contract is
S
T
— (see Appendix A). The credit exposure on a long forward
contract is therefore max(S
T
— , 0); that is, it is a call on the asset
price with strike price Similarly, the credit exposure on a short
forward contract is max( — S
T
, 0); that is, it is a put on the asset
price with strike price The total credit exposure is therefore a
straddle with strike price
12.11. As time passes, there is a tendency for the currency which has the
lower interest rate to strengthen. This means that a swap where we are
receiving this currency will tend to move in the money (i.e., have a
positive value). Similarly, a swap where we are paying the currency will
tend to move out of the money (i.e., have a negative value). From this it
follows that our expected exposure on the swap where we are receiving
the low-interest currency is much greater than our expected exposure on
the swap where we are receiving the high-interest currency. We should
therefore look for counterparties with a low credit risk on the side of the
swap where we are receiving the low-interest currency. On the other side
of the swap, we are far less concerned about the creditworthiness of the
counterparty.
CHAPTER 13
13.1. Both provide insurance against a particular company defaulting
during a period of time. In a credit default swap, the payoff is the
notional principal amount multiplied by one minus the recovery rate.
In a binary swap the payoff is the notional principal.
13.2. The seller receives 300,000,000 x 0.0060 x 0.5 = $900,000 at times
0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0 years. The seller also receives a final
accrual payment of about $300,000 (= $300,000,000 x 0.060 x 2/12) at
448
Answers to Problems and Questions
the time of the default (4 years and 2 months). The seller pays
300,000,000 x 0.6 = $180,000,000 at the time of the default.
13.3. Sometimes there is physical settlement and sometimes there is cash
settlement. In the event of a default when there is physical settlement, the
buyer of protection sells bonds issued by the reference entity for their face
value. Bonds with a total face value equal to the notional principal can be
sold. In the event of a default when there is cash settlement, a calculation
agent estimates the value of the Cheapest-to-deliver bond issued by the
reference entity a specified number of days after the default event. The
cash payoff is then based on the excess of the face value of these bonds
over the estimated value.
13.4. A cash CDO is created from a bond portfolio. The returns from the
bond portfolio flow to a number of tranches (i.e., different categories of
investors). The tranches differ as far as the credit risk they assume. The
first tranche might have an investment in 5% of the bond portfolio and be
responsible for the first 5% of losses. The next tranche might have an
investment in 10% of the portfolio and be responsible for the next 10%
of the losses, and so on. In a synthetic CDO there is no bond portfolio.
Instead, a portfolio of credit default swaps is sold and the resulting credit
risks are allocated to tranches in a similar way to that just described.
13.5. In a first-to-default basket CDS, there are a number of reference
entities. When the first one defaults, there is a payoff (calculated in the
usual way for a CDS) and the basket CDS terminates. The value of the
protection given by the first-to-default basket CDS decreases as the
correlation between the reference entities in the basket increases. This is
because the probability of a default decreases as the correlation increases.
In the limit when the correlation is 1, there is in effect only one company
and the probability of a default is quite low.
13.6. Risk-neutral default probabilities are backed out from credit default
swaps or bond prices. Real-world default probabilities are calculated from
historical data.
13.7. Suppose a company wants to buy some assets. If a total return swap
is used, a financial institution buys the assets and enters into a swap with
the company where it pays the company the return on the assets and
receives from the company LIBOR plus a spread. The financial institu-
tion has less risk than it would have if it lent the company money and
used the assets as collateral. This is because, in the event of a default by
the company, it owns the assets.
Answers to Problems and Questions 449
13.8. An analysis similar to that in Tables 13.1 to 13.4 gives the PV of
expected payments as 3.7364s, the PV of the expected payoff as 0.0838,
and the PV of the expected accrual payment as 0.05985. The credit default
swap spread is 221 basis points.
13.9. If the credit default swap spread is 150 basis points, the value of the
swap to the buyer of protection is
0.0838 - (3.7364 + 0.0598) x 0.0150 = 0.0269
per dollar of notional principal.
13.10. If the swap is a binary CDS, the present value of expected payoffs
is 0.1197 and the credit default swap spread is 315 basis points.
13.11. A 5-year nth-to-default credit default swap works in the same way
as a regular credit default swap except that there is a basket of companies.
The payoff occurs when the nth default from the companies in the basket
occurs. After the nth default has occurred, the swap ceases to exist. When
n = 1 (so that the swap is a "first to default"), an increase in the default
correlation lowers the value of the swap to the protection buyer. When
n = 25 (so that the swap is a 25th to default), an increase in the default
correlation increases the value of the swap to the protection buyer.
13.12. The recovery rate of a bond is usually defined as the value of the
bond a few days after a default occurs as a percentage of the bond's face
value.
13.13. The payoff from a plain vanilla CDS is 1 — R times the payoff
from a binary CDS with the same principal. The payoff always occurs at
the same time on the two instruments. It follows that the regular pay-
ments on a new plain vanilla CDS must be 1 - R times the payments on a
new binary CDS. Otherwise there would be an arbitrage opportunity.
13.14. In the case of a total return swap, a company receives (pays) the
increase (decrease) in the value of the bond. In a regular swap this does
not happen.
13.15. When a company enters into a long (short) forward contract it is
obligated to buy (sell) the protection given by a specified credit default
swap with a specified spread at a specified future time. When a company
buys a call (put) option contract, it has the option to buy (sell) the
protection given by a specified credit default swap with a specified spread
at a specified future time. Both contracts are normally structured so that
they cease to exist if a default occurs during the life of the contract.
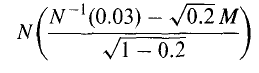
450
Answers to Problems and Questions
13.16. A credit default swap insures a corporate bond issued by the
reference entity against default. Its approximate effect is to convert the
corporate bond into a risk-free bond. The buyer of a credit default swap
has therefore chosen to exchange a corporate bond for a risk-free bond
This means that the buyer is long a risk-free bond and short a similar
corporate bond.
13.17. Payoffs from credit default swaps depend on whether a particular
company defaults. Arguably some market participants have more
information about this that others (see Business Snapshot 13.2).
13.18. Real-world default probabilities are less than risk-neutral default
probabilities. It follows that the use of real-world default probabilities
will tend to understate the value of the protection.
13.19. In an asset swap the bond's promised payments are swapped for
LIBOR plus a spread. In a total return swap the bond's actual payments
are swapped for LIBOR plus a spread.
13.20. Using equation (13.2), we find that the probability of default
conditional on a factor value of M is
For M equal to -2, — 1, 0, 1, 2, the probabilities of default are 0.135,
0.054, 0.018, 0.005, 0.001, respectively. To six decimal places, the prob-
ability of more that 10 defaults for these values of M can be calculated
using the BINOMDIST function in Excel. They are 0.959284, 0.79851,
0.000016, 0, 0, respectively.
13.21. For a CDO squared we form a portfolio of CDO tranches and
tranche the default losses in a similar way to Figure 13.3. For a CDO
cubed we form a portfolio of CDO squared tranches and tranche the
default losses in a similar way to Figure 13.3.
CHAPTER 14
14.1. The definition includes all internal risks and external risks except
reputational risk and risks resulting from strategic decisions.
14.2. Based on the results reported in Section 14.4, the loss would be
100 x 3
0.23
, or $127.8 million.
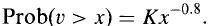
Answers to Problems and Questions 451
14.3. , When x = 20, the probability is 0.1. This
means that K = 1.0986. The probability of the specified losses being
exceeded are (a) 5.74%, (b) 3.30%, and (c) 1.58%.
14.4. Moral hazard is handled by deductibles and by making premiums
dependent on past claims. Adverse selection is handled by finding out as
much as possible about a driver before insurance is granted and then
modifying premiums as more information on the driver becomes available.
14.5. CEOs must prepare a statement asserting that the financial state-
ments are accurate. They must return bonuses in the event that there is a
restatement of financial statements.
14.6. If a trader operates within established risk limits and takes a loss, it
is part of market risk. If risk limits are violated, the loss becomes
classified as an operational risk.
14.7. (a) It is unlikely that an individual would not look after his or her
health because of the existence of a life insurance contract. But it has been
known for the beneficiary of a life insurance contract to commit murder
to receive the payoff from the contract! (b) Individuals with short life
expectancies are more likely to buy life insurance than individuals with
long life expectancies.
14.8. External loss data is data relating to the losses of other banks. It is
data obtained from sharing agreements with other banks or from data
vendors. External data is used to determine relative loss severity. It can be
a useful indicator of the ratio of mean losses in Business Unit A to mean
losses in Business Unit B or the ratio of the standard deviation of losses
in Business Unit A to the standard deviation of losses in Business Unit B.
14.9. The Poisson distribution is commonly used for loss frequency. The
lognormal distribution is commonly used for loss severity.
14.10. Two examples of key risk indicators are staff turnover and number
of failed transactions.
14.11. When the loss frequency is 3, the mean total loss is about 3.3 and
the standard deviation is about 2.0. When the loss frequency is increased
to 4, the mean loss is about 4.4 and the standard deviation is about 2.4.
CHAPTER 15
15.1. Leverage and Crashophobia.
15.2. Uncertain volatility and jumps.
452
Answers to Problems and Questions
15.3. When plain vanilla call and put options are being priced, traders do
use the Black-Scholes model as an interpolation tool. They calculate
implied volatilities for the options that are actively traded. By interpolat-
ing between strike prices and between times to maturity, they estimate
implied volatilities for other options. These implied volatilities are then
substituted into Black-Scholes to calculate prices for these options.
Black-Scholes is more than an interpolation tool when used for hedging.
15.4. 13.45%. We get the same answer by (a) interpolating between strike
prices of 1.00 and 1.05 and then between maturities of 6 months and
1 year and (b) interpolating between maturities of 6 months and 1 year
and then between strike prices of 1.00 and 1.05.
15.5. The models of physics describe the behavior of physical processes.
The models of finance ultimately describe the behavior of human beings.
15.6. It might notice that it is getting a large amount of business of a
certain type because it is quoting prices different from its competitors.
The pricing differences may also become apparent if it decides to unwind
transactions and approaches competitors for quotes. Also, it might
subscribe to a service where it obtains the average price quotes by dealers
for particular transactions.
15.7. A loss equal to half the bid-offer spread is recognized when
positions are liquidated. Liquidity VaR takes this loss into account.
15.8. Liquidity black holes occur when most market participants want to
be on one side of a market. Regulation is liable to lead to liquidity black
holes. This is because when all financial institutions are regulated in the
same way they tend to want to respond to external economic events in the
same way.
15.9. Within-model hedging involves hedging against changes in variables
that the model assumes to be stochastic. Outside-model hedging involves
hedging against parameters that the model assumes to be constant.
15.10. The Black-Scholes model assumes that the probability distribu-
tion of the stock price in 1 month is lognormal. In this case it is clearly
not lognormal. Possibly it consists of two lognormal distributions super-
imposed upon each other and is bimodal. Black-Scholes is clearly
inappropriate.
15.11. In this case the probability distribution of the exchange rate has a
thin left tail and a thin right tail relative to the lognormal distribution.
Deep-out-of-the-money calls and puts will have relatively low prices.
Answers to Problems and Questions
453
15.12. The term "marking to market" refers to the practice of revaluing
instruments (usually daily) so that they are consistent with the market.
The prices calculated for actively traded products do reflect market prices.
The model is used merely as an interpolation tool. The term "marking to
market" is therefore accurate for these products. The prices for structured
products depend on the model being used. Hence the term "marking to
model".
15.13. Hedge funds are not regulated in the same way as other financial
institutions and can therefore be contrarian investors buying whenever
everyone else is selling and selling whenever everyone else is buying.
However, black holes can be created when large numbers of hedge funds
follow similar trading strategies.
CHAPTER 16
16.1. Economic capital is a bank's own estimate of the capital it requires.
Regulatory capital is the capital it is required to keep by bank supervisors.
16.2. A company with an AA rating has a 0.03% chance of defaulting in
1 year.
16.3. Business risk includes risks relating to strategic decisions and
reputation.
16.4. The models used for economic capital are likely to be broadly
similar to those used to calculate regulatory capital in the case of market
risk and operational risk. When calculating credit risk economic capital, a
bank may consider it appropriate to use a different credit correlation
model and different correlation parameters from those used in regulatory
capital calculations.
16.5. The 99.97% worst-case value of the logarithm of the loss is
0.5 + 4 x 3.43 = 14.23. The 99.97% worst-case loss is therefore $1,510
million. From the properties of the lognormal distribution, the expected
loss is exp(0.5+ 4
2
/2), or $4,915. The capital requirement is therefore
$1.505 million.
16.6. The economic capital for Business Unit 1 is 96.85. The economic
capital for Business Unit 2 is 63.87. The total capital is 124.66.
16.7. The incremental effect of Business Unit 1 on total economic
capital is 60.78. The incremental effect of Business Unit 2 on total
economic capital is 27.81. This suggests that 60.78/(60.78 + 27.81), or
68.61%, of economic capital should be allocated to Business Unit 1 and
27.81/(60.78 + 27.81), or 31.39%, to Business Unit 2. The marginal
454
Answers to Problems and Questions
effect of increasing the size of Business Unit 1 by 0.5% is 0.4182. The
marginal effect of increasing the size of Business Unit 2 by 0.5% is
0.2056. Euler's theorem is satisfied because the total economic capital is
approximately equal to the sum of 0.4182/0.005 and 0.2056/0.005.
16.8. The capital is 40 — 2 = $38 million and the return before tax is
12 - 5 - 2 = $5 million. The before-tax RAROC is therefore 13.2%. In
practice, the allocation of diversification benefits to this venture might
reduce capital and increase RAROC.
16.9. RAROC can be used to compare the past performance of different
business units or to project the expected future performance of business
units.
CHAPTER 17
17.1. A day's HDD is max(0, 65 - A) and a day's CDD is max(0, A - 65),
where A is the average of the highest and lowest temperature during the day
at a specified weather station, measured in degrees Fahrenheit.
17.2. It is an agreement by one side to deliver a specified amount of gas at
a roughly uniform rate during a month to a particular hub for a specified
price.
17.3. The average temperature each day is 75° Fahrenheit. The CDD each
day is therefore 10 and the cumulative CDD for the month is
10 x 31 = 310. The payoff from the call option is therefore
(310 - 250) x 5,000 = $300,000
17.4. Unlike most commodities electricity cannot be stored easily. If the
demand for electricity exceeds the supply, as it sometimes does during the
air-conditioning season, the price of electricity in a deregulated environ-
ment will skyrocket. When supply and demand become matched again,
the price will return to former levels.
17.5. HDD is max(65 — A, 0), where A is the average of the maximum
and minimum temperature during the day. This is the payoff from a put
option on A with a strike price of 65. CDD is max(A — 65, 0). This is the
payoff from call option on A with a strike price of 65.
17.6. It would be useful to calculate the cumulative CDD for July of each
year of the last 50 years. A linear regression relationship
CDD = a + bt + e
Answers to Problems and Questions 455
could then be estimated, where a and b are constants, t is the time in years
measured from the start of the 50 years, and e is the error. This relation-
ship allows for linear trends in temperature through time. The expected
CDD for next year (year 51) is then a + 5\b. This could be used as an
estimate of the forward CDD.
17.7. The volatility of the one-year forward price will be less than the
volatility of the spot price. This is because, when the spot price changes
by a certain amount, mean reversion will cause the forward price will
change by a lesser amount.
17.8. The energy producer faces quantity risks and price risks. It can use
weather derivatives to hedge the quantity risks and energy derivatives to
hedge against the price risks.
17.9. A 5 x 8 contract for May 2006 is a contract to provide electricity
for 5 days per week during the off-peak period (11 p.m. to 7 a.m.). When
daily exercise is specified, the holder of the option is able to choose each
weekday whether he or she will buy electricity at the strike price at the
agreed rate. When there is monthly exercise, he or she chooses once at the
beginning of the month whether electricity is to be bought at the strike
price at the agreed rate for the whole month. The option with daily
exercise is worth more.
17.10. CAT bonds (catastrophe bonds) are an alternative to reinsurance
for an insurance company that has taken on a certain catastrophic risk
(e.g., the risk of a hurricane or an earthquake) and wants to get rid of it.
CAT bonds are issued by the insurance company. They provide a higher
rate of interest than government bonds. However, the bondholders agree
to forego interest, and possibly principal, to meet any claims against the
insurance company that are within a prespecified range.
17.11. The CAT bond has very little systematic risk. Whether a particular
type of catastrophe occurs is independent of the return on the market.
The risks in the CAT bond are likely to be largely "diversified away" by
the other investments in the portfolio. A B-rated bond does have sys-
tematic risk that cannot be diversified away. It is likely therefore that the
CAT bond is a better addition to the portfolio.
17.12. It means that the price of the energy source will be pulled back to
a long-run average level. Electricity has the highest mean-reversion rate;
oil has the lowest.

Glossary of Terms
Accrued Interest The interest earned on a bond since the last coupon
payment date.
Add-on Factor When the credit equivalent amount for a derivatives
transaction is being calculated, this is the percentage of principal added
to the current exposure to allow for possible future changes in the value
of the derivative.
Advanced Measurement Approach The way in which the most sophisti-
cated banks will be allowed to calculate regulatory capital for operational
risk under Basel II.
Adverse Selection The phenomenon that, if an insurance company
offers the same premiums to everyone, it tends to end up providing
coverage for the worst risks.
American Option An option that can be exercised at any time during its
life.
Analytic Result Result where answer is in the form of an equation.
Arbitrage A trading strategy that takes advantage of two or more secur-
ities being mispriced relative to each other.
Arbitrage Pricing Theory A theory where the return from an investment
is assumed to depend on several factors.
Arbitrageur An individual engaging in arbitrage.
