Хмельова Р.М. Методичні вказівки з виконання контрольної роботи № 1 з дисципліни Нарисна геометрія для студентів-заочників
Подождите немного. Документ загружается.

Будуються проекції відстані в заданій системі площин проекцій. Тому
що с
1
k
1
дорівнює - ИВ відстані, тобто є горизонтальною прямою
(паралельною Н
1
), то його фронтальна проекція паралельна осі Х
2
(чи
перпендикулярна a
1
'b
1
'). У проекційному зв'язку знаходиться
горизонтальна (ck) і фронтальна (с
k
) проекції відстані.
5. Визначити відстань між паралельними прямими
Для визначення відстані між паралельними прямими обидві прямі
подвійною заміною площин проекцій треба зпроекціювати у точки, як це
було виконано в попередній задачі з прямої АВ (див. рис. 8).
Відстань між цими точками і буде ИВ відстані між паралельними
прямими.
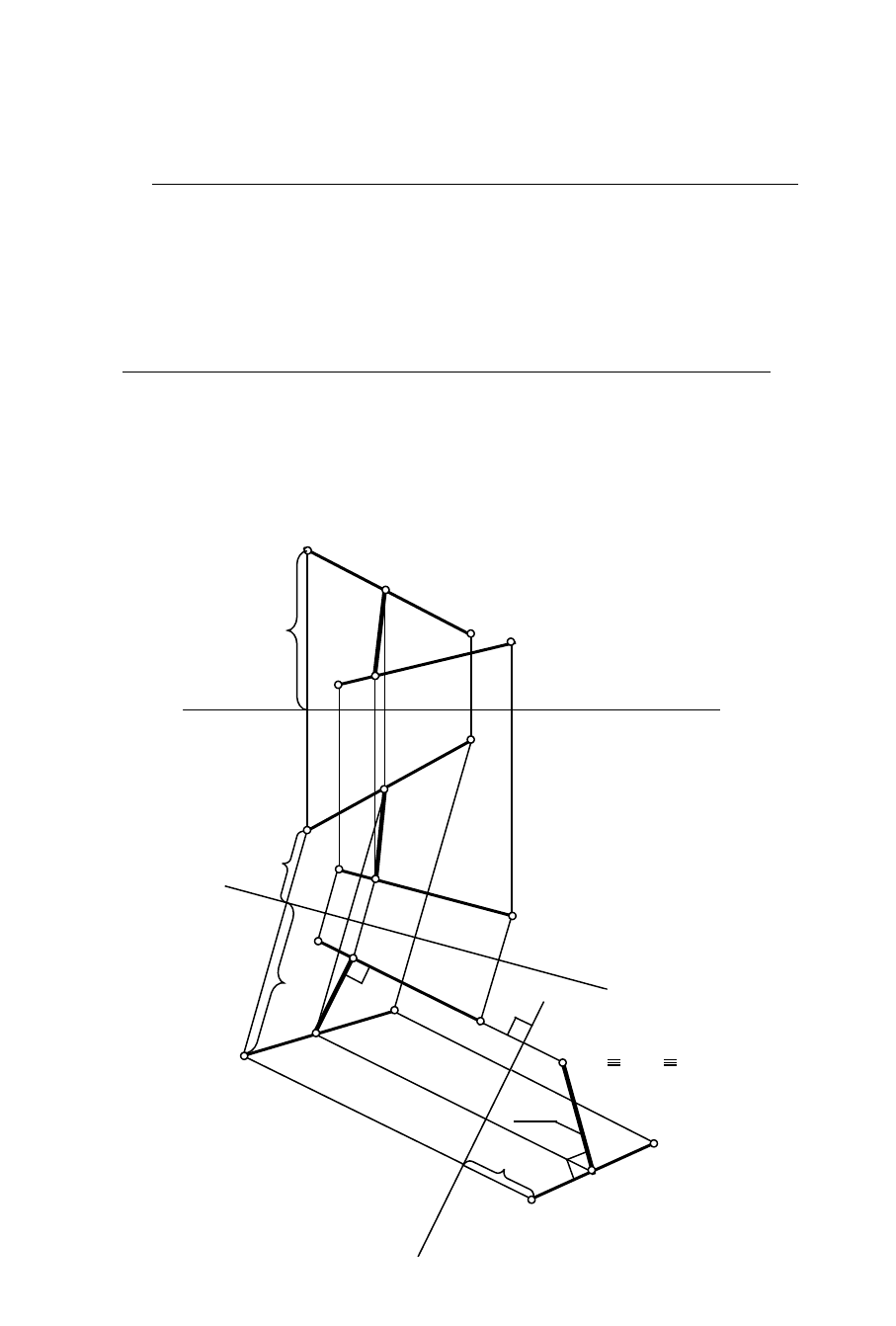
6. Визначити відстань між перехресними прямими
Відстань між перехресними прямими визначається відрізком прямої,
перпендикулярної до обох прямих.
Дано перехресні прямі загального положення АВ (аb, а'b') і CD (cd,
c'd') (рис. 9). Потрібно визначити ИВ відстані між ними.
Рис. 9. Визначення відстані між перехресними прямими
11
X
H
V
1
X
1
b´
c´
a
X
2
Н
1
V
1
с
1
ИВ
a´
k´
z
a
a
1
b
1
k
1
k
1
´
b
1
´
a
1
´
c
b
k
d
1
e
1
y
a
d
1
´
.
.
y
a
z
a
d´
e´
V
Н
e
d
c
1
´
e
1
´
.
Для цього треба одну з прямих зпроекціювати подвійною заміною
площин проекцій у точку. У даній задачі це - пряма CD. У першій заміні
площина V
1
паралельна CD (на епюрі вісь X
1
паралельна сd), у другій
заміні площина Н
1
перпендикулярна прямій CD (на епюрі вісь X
2
перпендикулярна с
1
'd
1
'), при цьому пряма CD зпроекціюється у точку
с
1
d
1
. Опустивши перпендикуляр із точки с
1
d
1
на a
1
b
1
, одержують ИВ
відстані між прямими (ця відстань позначена відрізком e
1
k
1
). Далі
будуються проекції відстані: відрізок k
1
'e
1
' паралельний осі Х
2
; у
проекційному зв'язку знайдені горизонтальна (ke) і фронтальна (к'е')
проекції відстані в заданій системі площин проекцій.
7. Визначити відстань від вершини трикутника
до протилежної його сторони
Для розв’язання цієї задачі варто визначити ИВ трикутника і потім
опустити перпендикуляр з вершини трикутника на протилежну його
сторону. Зворотним проекціюванням побудувати проекції цього
перпендикуляра в заданій системі.
Як визначити ИВ трикутника див. рис. 7.
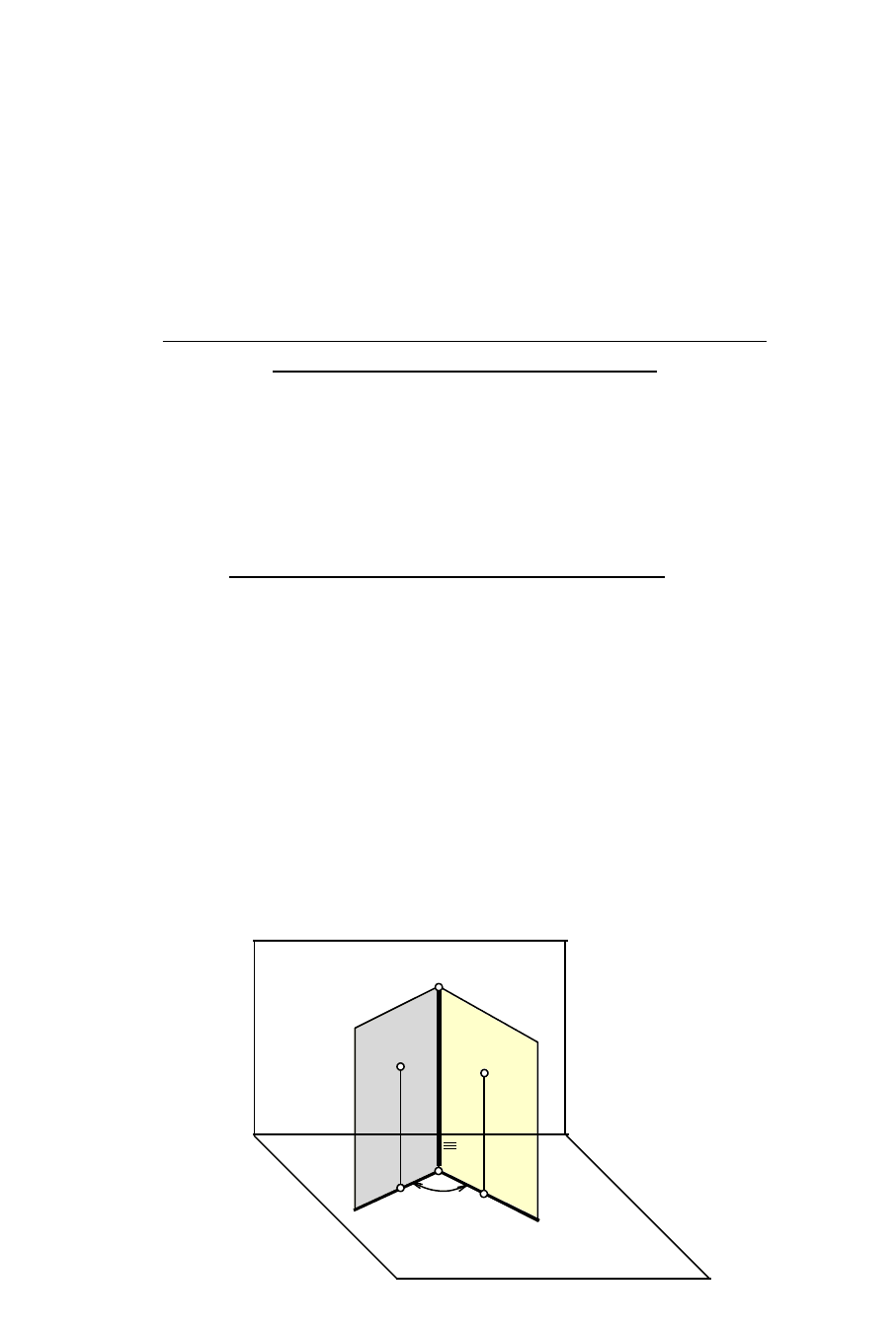
8. Визначити кут між площинами
Кут між площинами буде проекціюватися у ИВ, коли обидві площини
будуть перпендикулярні якій-небудь площині проекцій. У цьому випадку
лінія перетину площин буде проекціюватися на цю площину проекцій у
вигляді точки.
На просторовому кресленні (рис. 10) показані дві пересічні по лінії
МN площини Р и Q. Якщо площини перпендикулярні площині Н, то на неї
МN буде проекціюватися у точку. Якщо в кожній із площин узяти по
точці (точки A і B), то горизонтальні їхні проекції обов'язково будуть
проекціюватися на сліди-проекції цих площин, а тому що ці площини –
горизонтально-проекціюючі, то кут
, обмежений точками а, m
n, b, і є
шуканий кут між площинами.
Рис. 10 Загальний принцип визначення кута між площинами.
12
X
a b
V
Н
M
P
A
B
Q
N mn
ϕ
Q
н
P
н
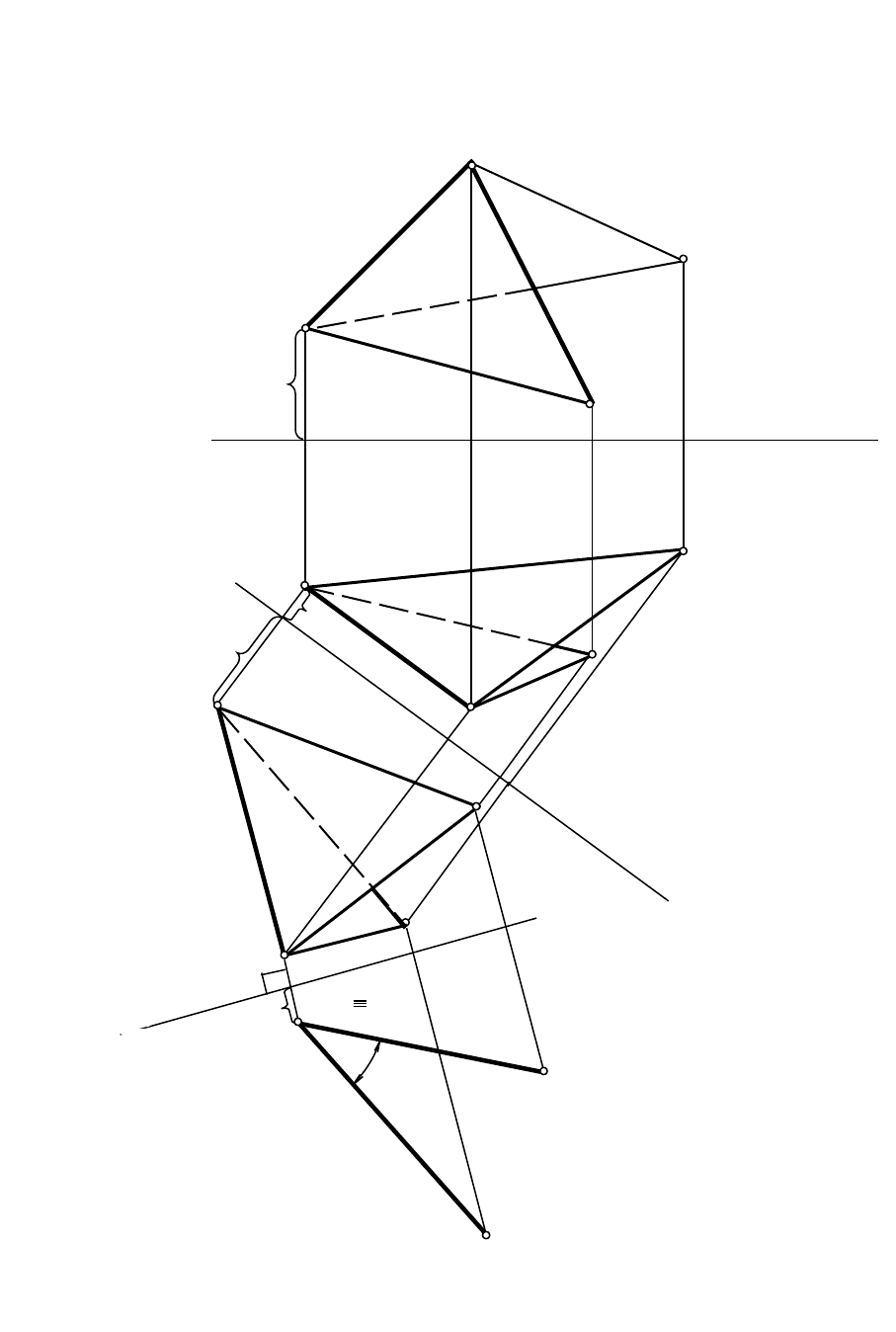
Рис. 11 Визначення кута між площинами, заданими трикутниками
13
X
H
V
1
X
1
b´
c´
a
с
1
a´
z
a
b
1
b
1
´
a
1
´
c
b
d
1
y
a
d
1
´
y
a
z
a
d´
V
Н
d
c
1
´
.
a
1
X
1
V
1
H
1

На рис. 11 площини задані трикутниками ABC (abс, a'b'с') і АВD (abd,
a'b'd'), що перетинаються по лінії АВ(ab, a'b'). У площині АВС узята
точка С(с, с') і точка D(d, d') - у трикутнику АВD. Подвійна ЗПП пряма АВ
проекціюється у точку a
1
b
1
, а також побудовані проекції точок C і D. Кут
- шуканий кут. Подвійною ЗПП площини загального положення
перетворилися в горизонтально-проекціюючі площини.
9. Визначити кут між гранями піраміди SBC і SDC.
Задача розв’язується аналогічно попередній. Потрібно лінію перетину
цих граней зпроекціювати в точку. Загальною лінією для цих граней
(лінією їхнього перетину) буде в даному випадку ребро піраміди SC.
Отже подвійною заміною площин проекцій ребро SC треба
зпроекціювати в точку, як у задачі 7 (рис. 11), а також у кожній із граней
взяти по одній точці, наприклад точку B у грані SBC і точку D у грані SDC.
10. Визначити кут нахилу трикутника ABC до площини H (кут
).
Для цього даний трикутник треба однією заміною площин проекцій
перетворити у фронтально–проекціюючу, для чого в ньому треба провести
горизонталь і провести нову площину проекцій V
1
перпендикулярно цій
горизонталі і площині заданого трикутника. Трикутник ABC буде
проекціюватися на площину V
1
у лінію a
1
'b
1
'c
1
'. Кут між цією лінією і
віссю X
1
буде
(див. рис. 6 а і 7).
Якщо необхідно визначити кут нахилу до площини V -
, то треба
в площині заданого трикутника взяти фронталь і замінити площину H на
H
1
, щоб площина трикутника стала горизонтально–проекціюючою.
14

Подписано к печати 2.12.03. Изд. № 153/03. Зак. 459/2003. Тираж 50 экз.
Объем 1 п.л. Усл. печ. л. 0,93. Уч.-изд. л. 0,98
Формат бумаги 60 х 84 1/16
15
16
