Hibbeler R.C. Structural Analysis

Подождите немного. Документ загружается.

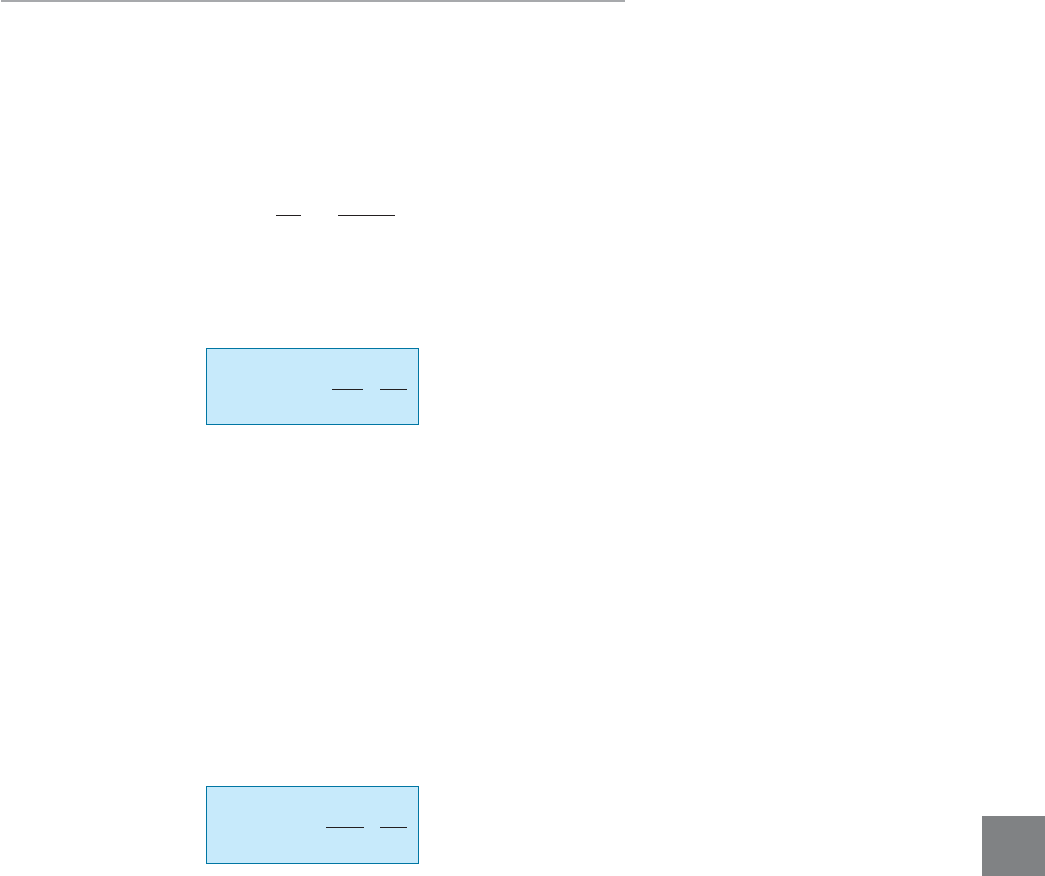
The beam shown in Fig. 9–26a is used in a building subjected to two

different thermal environments. If the temperature at the top surface

of the beam is 80°F and at the bottom surface is 160°F, determine the

vertical deflection of the beam at its midpoint due to the temperature

gradient. Take a = 6.5110

-6

2>°F.

EXAMPLE 9.13

380 CHAPTER 9DEFLECTIONS USING ENERGY M ETHODS

10 in.

80 F

160 F

10 ft

(a)

1 lb

5 ft 5 ft

x x

m 

(b)

Fig. 9–26

SOLUTION

Since the deflection at the center of the beam is to be determined, a

virtual unit load is placed there and the internal virtual moment in the

beam is calculated, Fig. 9–26b.

The mean temperature at the center of the beam is

so that for application of Eq. 9–27,

Also, Applying the principle of virtual work,

we have

Ans.

The result indicates a very negligible deflection.

= 0.0936 in.

= 2

60 in.

6.5110

-6

2>°F140°F2

5 in.

1 lb

ma ¢T

c = 10 in.>2 = 5 in.40°F.

¢T

= 120°F - 80°F =120°F,

1160° + 80°2>2 =

9.9 CASTIGLIANO’S THEOREM FOR BEAMS AND FRAMES 381

9.9 Castigliano’s Theorem for Beams

and Frames

The internal bending strain energy for a beam or frame is given by

Eq. 9–11 Substituting this equation into Eq. 9–20

and omitting the subscript i, we have

Rather than squaring the expression for internal moment M, integrating,

and then taking the partial derivative, it is generally easier to differentiate

prior to integration. Provided E and I are constant, we have

(9–28)

where

external displacement of the point caused by the real loads

acting on the beam or frame.

external force applied to the beam or frame in the direction of

internal moment in the beam or frame, expressed as a function of

x and caused by both the force P and the real loads on the beam.

modulus of elasticity of beam material.

moment of inertia of cross-sectional area computed about the

neutral axis.

If the slope at a point is to be determined, we must find the partial

derivative of the internal moment M with respect to an external couple

moment acting at the point, i.e.,

(9–29)

The above equations are similar to those used for the method of

virtual work, Eqs. 9–22 and 9–23, except and replace m

and respectively. As in the case for trusses, slightly more calculation

is generally required to determine the partial derivatives and apply

Castigliano’s theorem rather than use the method of virtual work. Also,

recall that this theorem applies only to material having a linear elastic

response. If a more complete accountability of strain energy in the

structure is desired, the strain energy due to shear, axial force, and

torsion must be included. The derivations for shear and torsion follow

the same development as Eqs. 9–25 and 9–26. The strain energies and

their derivatives are, respectively,

0M>0M¿0M>0P

u =

0M¿

M¿

I =

E =

M =

¢. P =

¢=

2EI

1¢

=0U

>0P

dx>2EI2.

382 CHAPTER 9DEFLECTIONS USING ENERGY M ETHODS

Procedure for Analysis

The following procedure provides a method that may be used to

determine the deflection and/or slope at a point in a beam or frame

using Castigliano’s theorem.

External Force

or Couple Moment

• Place a force P on the beam or frame at the point and in the

direction of the desired displacement.

• If the slope is to be determined, place a couple moment at the

point.

• It is assumed that both P and have a variable magnitude in

order to obtain the changes or

Internal Moments

• Establish appropriate x coordinates that are valid within regions

of the beam or frame where there is no discontinuity of force,

distributed load, or couple moment.

• Calculate the internal moment M as a function of P or and

each x coordinate. Also, compute the partial derivative or

for each coordinate x.

• After M and or have been determined, assign P

or its numerical value if it has replaced a real force or couple

moment. Otherwise, set P or equal to zero.

Castigliano’s Theorem

• Apply Eq. 9–28 or 9–29 to determine the desired displacement

or slope It is important to retain the algebraic signs for

corresponding values of M and or

• If the resultant sum of all the definite integrals is positive, or

is in the same direction as P or M¿.

u¢

0M>0M¿.0M>0P

u.¢

M¿

0M>0M¿0M>0P

0M>0M¿

0M>0P

M¿

0M>0M¿.0M>0P

M¿

These effects, however, will not be included in the analysis of the

problems in this text since beam and frame deflections are caused mainly

by bending strain energy. Larger frames, or those with unusual geometry,

can be analyzed by computer, where these effects can readily be

incorporated into the analysis.

2JG

b dx

= K

2AG

b dx

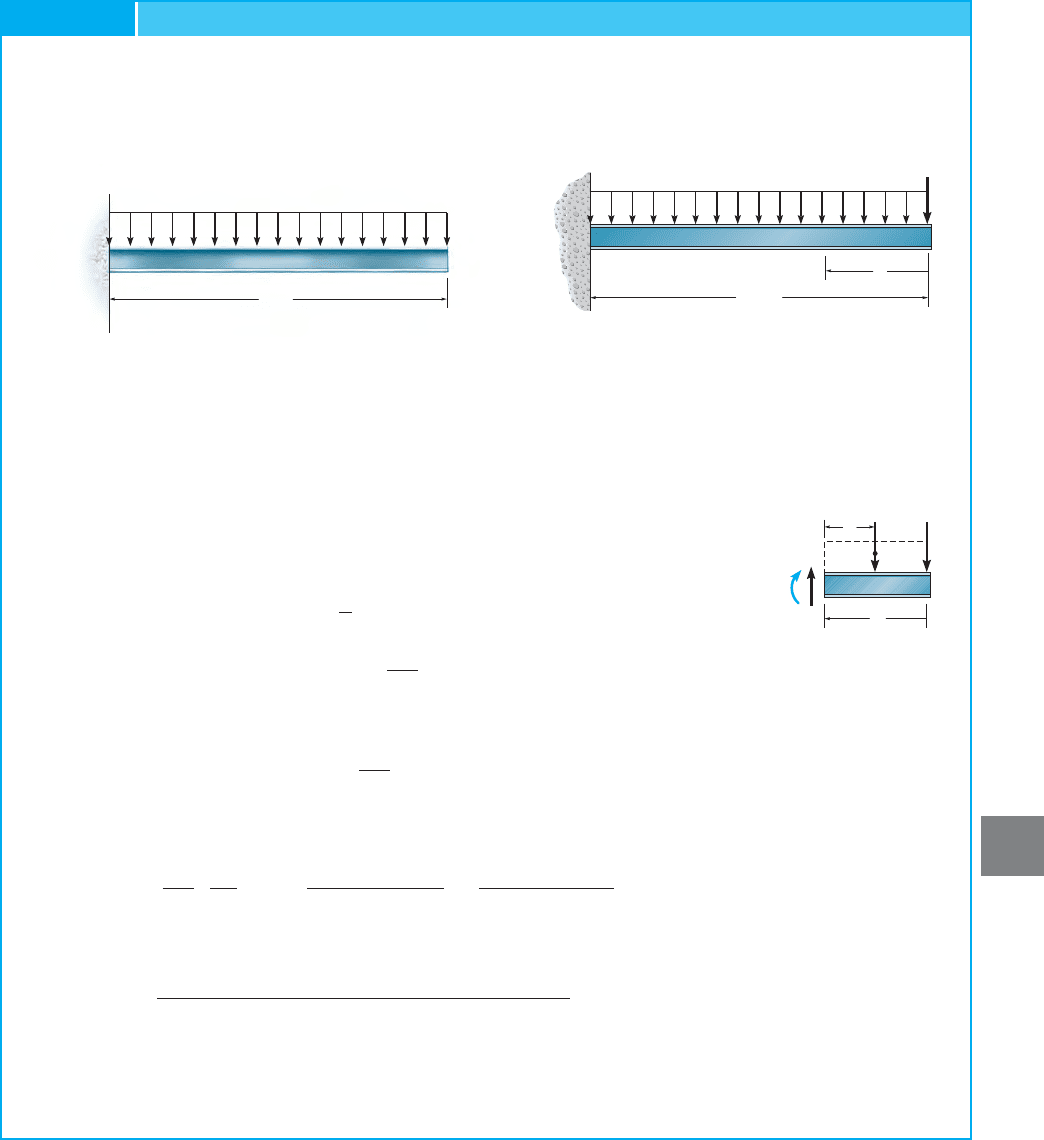
EXAMPLE 9.14

Determine the displacement of point B of the beam shown in

Fig. 9–27a. Take I = 500110

2 mm

.E = 200 GPa,

9.9 CASTIGLIANO’S THEOREM FOR BEAMS AND FRAMES 383

Fig. 9–27

12 kN/ m

10 m

(b)

12 kN/m

10 m

(a)

12 x

(c)

SOLUTION

External Force

. A vertical force P is placed on the beam at B as

shown in Fig. 9–27b.

Internal Moments

. A single x coordinate is needed for the

solution, since there are no discontinuities of loading between A and

B. Using the method of sections, Fig. 9–27c, we have

Setting , its actual value, yields

Castigliano’s Theorem. Applying Eq. 9–28, we have

Ans.

The similarity between this solution and that of the virtual-work

method, Example 9–7, should be noted.

= 0.150 m = 150 mm

15110

2 kN

200110

2 kN>m

[500110

2 mm

]110

-12

>mm

15110

2 kN

1-6x

21-x2 dx

M =-6x

=-x

P = 0

M =-6x

- Px

=-x

-M - 112x2a

b - Px = 0d +©M = 0;

384 CHAPTER 9DEFLECTIONS USING ENERGY M ETHODS

3 kN

(b)

M¿

Determine the slope at point B of the beam shown in Fig. 9–28a.Take

SOLUTION

External Couple Moment

Since the slope at point B is to be

determined, an external couple is placed on the beam at this point,

Fig. 9–28b.

Internal Moments

. Two coordinates, and must be used to

determine the internal moments within the beam since there is a

discontinuity, at B. As shown in Fig. 9–28b, ranges from A to B

and ranges from B to C. Using the method of sections, Fig. 9–28c,the

internal moments and the partial derivatives are computed as follows:

For

Castigliano’s Theorem. Setting , its actual value, and apply-

ing Eq. 9–29, we have

Ans.

The negative sign indicates that is opposite to the direction of the

couple moment Note the similarity between this solution and that

of Example 9–8.

M¿.

=-0.00938 rad

-112.5 kN

200110

2 kN>m

[60110

2 mm

]110

-12

>mm

1-3x

2102 dx

-315 + x

2112 dx

112.5 kN

0M¿

M¿=0

0M¿

= 1

= M¿-315 + x

- M¿+315 + x

2= 0d +©M = 0;

0M¿

= 0

=-3x

+ 3x

= 0d +©M = 0;

M¿,

M¿

I = 60110

2 mm

.E = 200 GPa,

EXAMPLE 9.15

3 kN

5 m

3 kN

M¿

(c)

Fig. 9–28

3 kN

5 m

(a)

5 m

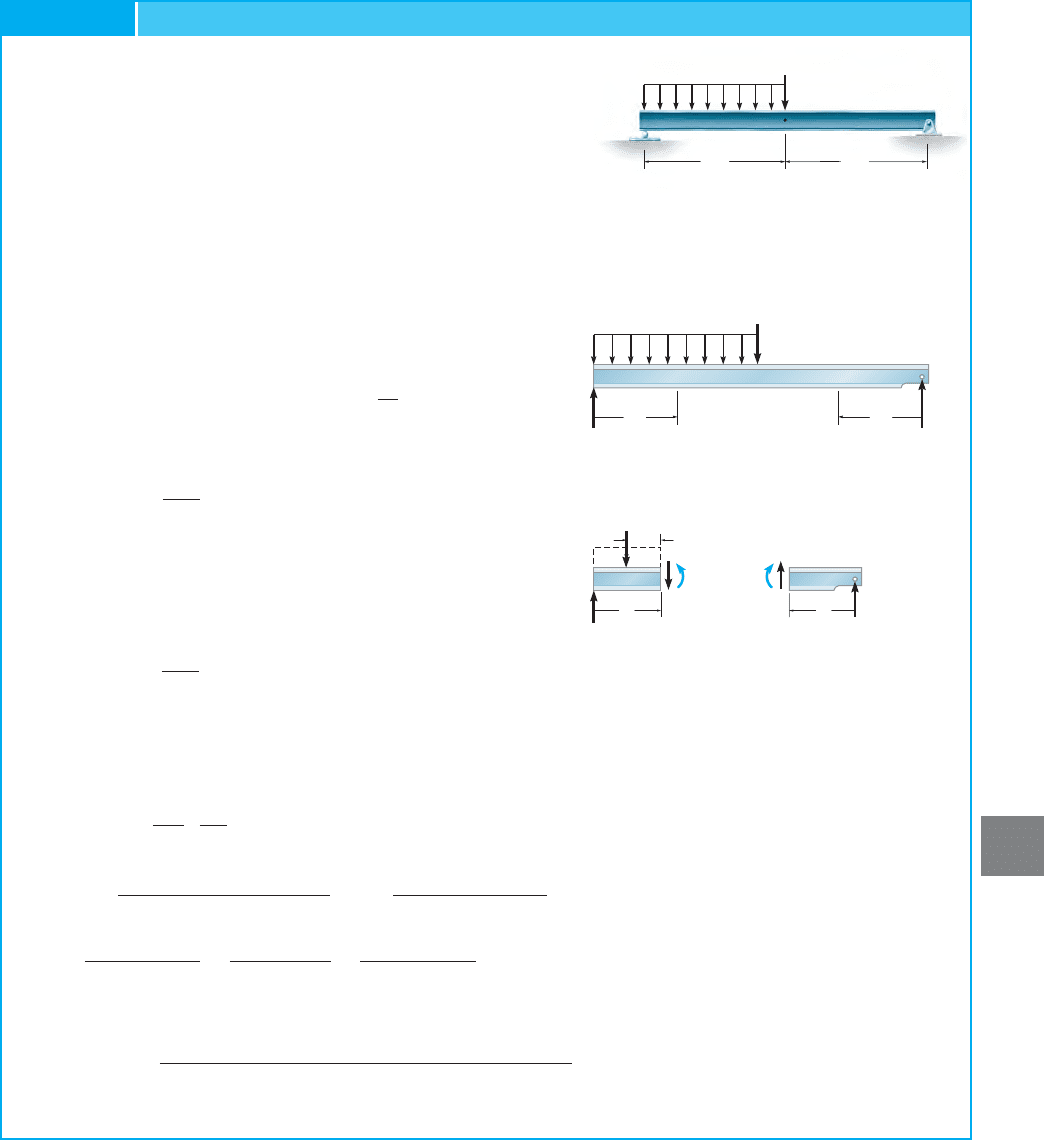
EXAMPLE 9.16

Determine the vertical displacement of point C of the beam

shown in Fig. 9–29a. Take

SOLUTION

External Force

. A vertical force P is applied at point C,

Fig. 9–29b. Later this force will be set equal to a fixed value of

20 kN.

Internal Moments

. In this case two x coordinates are needed for

the integration, Fig. 9–29b, since the load is discontinuous at C. Using

the method of sections, Fig. 9–29c, we have

For

Castigliano’s Theorem. Setting , its actual value, and

applying Eq. 9–28 yields

Ans. = 0.0142 m = 14.2 mm

426.7 kN

200110

2 kN>m

[150110

2 mm

]110

-12

>mm

234.7 kN

192 kN

426.7 kN

134x

- 4x

210.5x

2 dx

118x

210.5x

2 dx

P = 20 kN

= 0.5x

= 18 + 0.5P2x

-M

+ 18 + 0.5P2x

= 0d+©M = 0;

= 0.5x

= 124 + 0.5P2x

- 4x

-(24 + 0.5P2x

+ 8x

b + M

= 0d+©M = 0;

I = 150110

2 mm

.E = 200 GPa,

9.9 CASTIGLIANO’S THEOREM FOR BEAMS AND FRAMES 385

20 kN

8 kN/m

4 m 4 m

(a)

8 kN/ m

24  0.5P

8  0.5P

(b)

24  0.5P

8  0.5P

___

(c)

Fig. 9–29

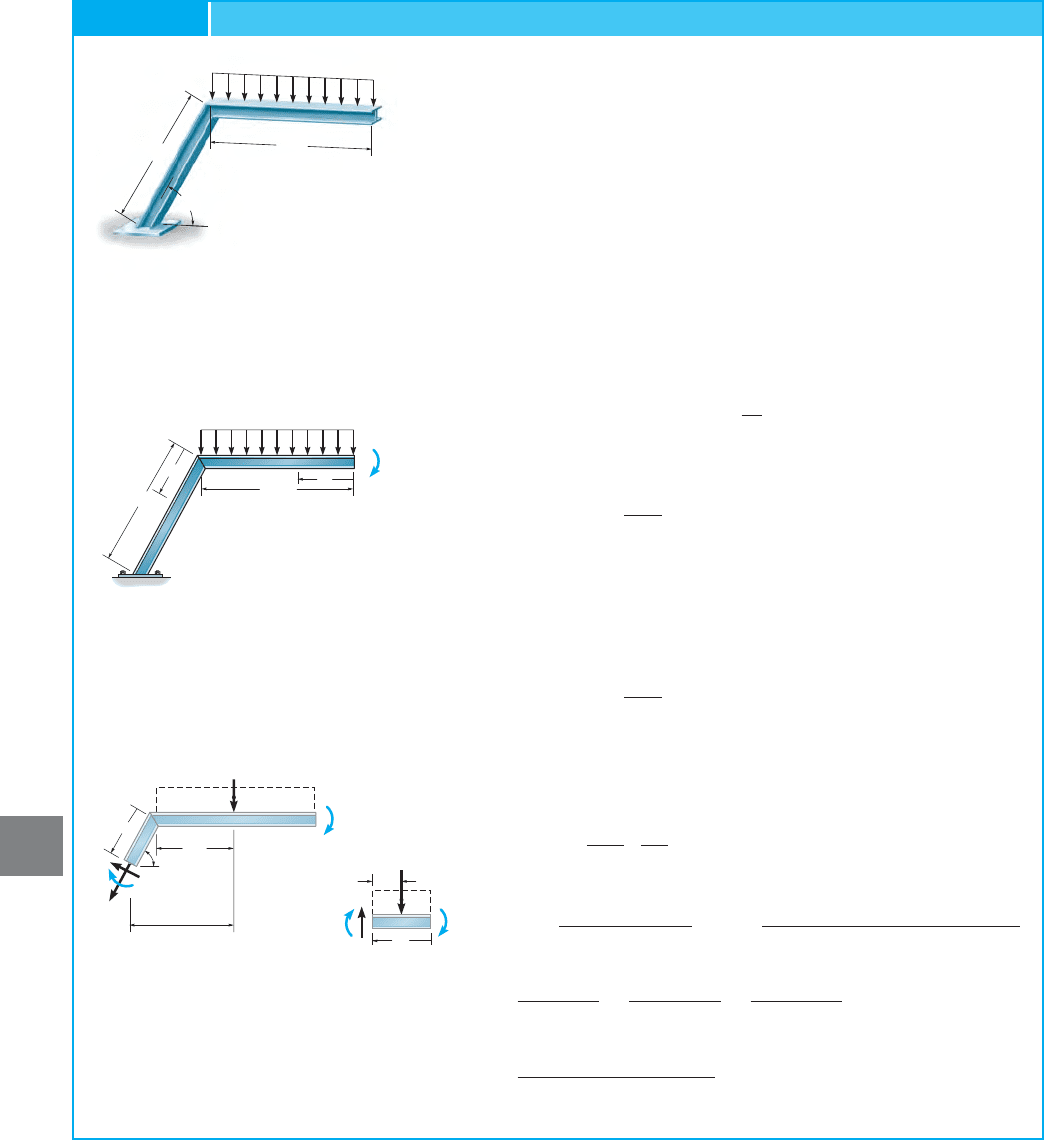
Determine the slope at point C of the two-member frame shown in

Fig. 9–30a. The support at A is fixed. Take

SOLUTION

External Couple Moment

A variable moment is applied to

the frame at point C, since the slope at this point is to be determined,

Fig. 9–30b. Later this moment will be set equal to zero.

Internal Moments

. Due to the discontinuity of internal loading

at B, two coordinates, and are chosen as shown in Fig. 9–30b.

Using the method of sections, Fig. 9–30c, we have

For

Castigliano’s Theorem. Setting and applying Eq. 9–29

yields

Ans.u

2616 k

1144 in

>ft

29110

2 k>in

1600 in

= 0.0216 rad

576 k

2040 k

2616 k

-x

1-12dx

-241x

cos 60° + 621-12dx

0M¿

M¿=0

0M¿

=-1

=-241x

cos 60° + 62- M¿

-M

- 241x

cos 60° + 62- M¿=0d+©M = 0;

0M¿

=-1

+ M¿

-M

- 2x

b - M¿=0d+©M = 0;

M¿¿.

I = 600 in

E = 29110

2 ksi,

EXAMPLE 9.17

386 CHAPTER 9DEFLECTIONS USING ENERGY M ETHODS

Fig. 9–30

12 ft

10 ft

60

2 k/ft

(a)

12 ft

10 ft

2 k/ft

M¿

(

)

6 ft

24 k

M¿

(c)

cos 60 6 ft

M¿

___

60

9.9 CASTIGLIANO’S THEOREM FOR BEAMS AND FRAMES 387

F9–13/9–14

3 m

4 kNm

30 kN

3 m

18 kN/m

3 m

12 kN

2 m2 m

4 m4 m

8 kN/m

6 m6 m

12 kN/m

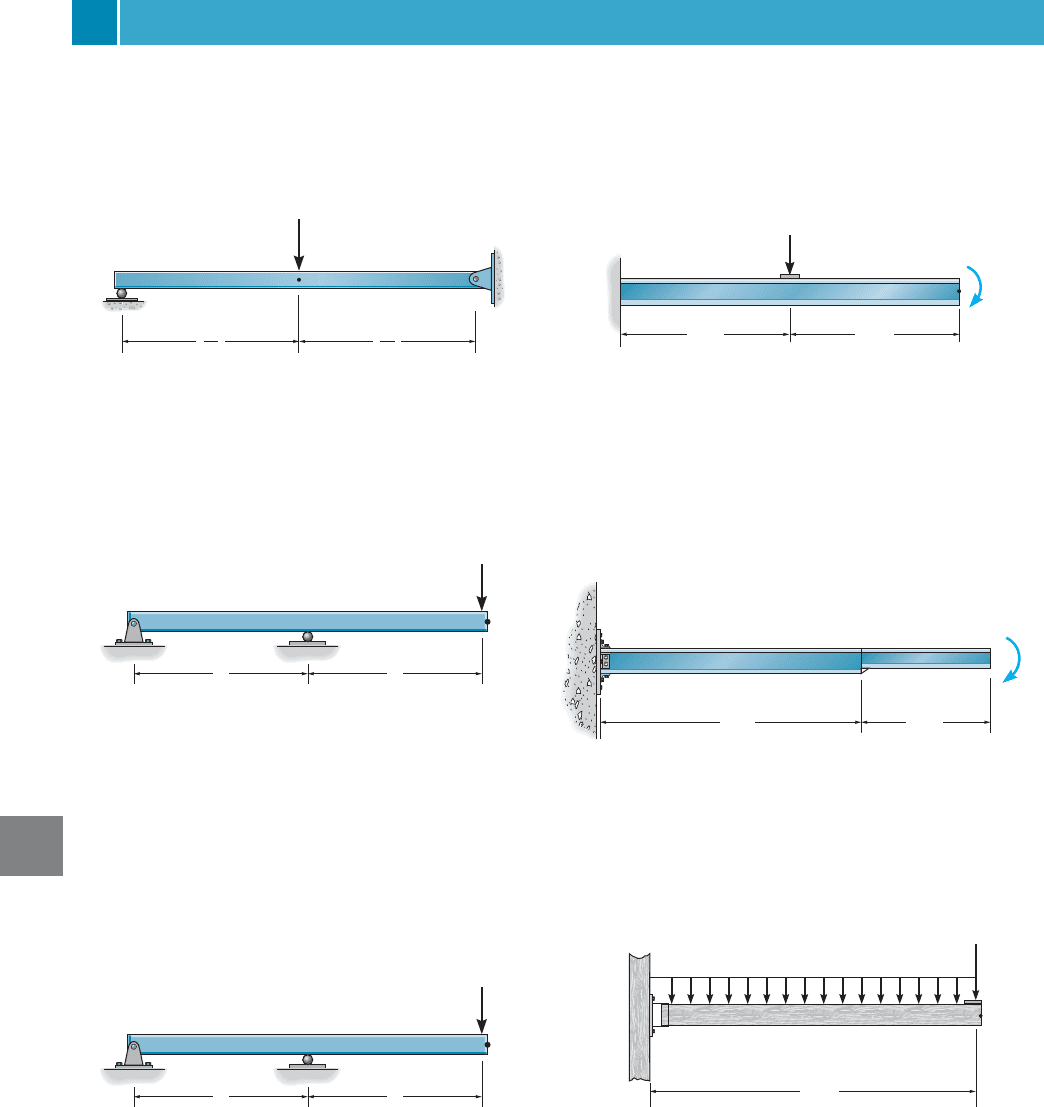
FUNDAMENTAL PROBLEMS

F9–13. Determine the slope and displacement at point A.

EI is constant. Use the principle of virtual work.

F9–14. Solve Prob. F9–13 using Castigliano’s theorem.

F9–19. Determine the slope at A and displacement at

point C. EI is constant. Use the principle of virtual work.

F9–20. Solve Prob. F9–19 using Castigliano’s theorem.

F9–15. Determine the slope and displacement at point A.

EI is constant. Use the principle of virtual work.

F9–16. Solve Prob. F9–15 using Castigliano’s theorem.

F9–21. Determine the slope and displacement at point C.

EI is constant. Use the principle of virtual work.

F9–22. Solve Prob. F9–21 using Castigliano’s theorem.

F9–17. Determine the slope and displacement at point B.

EI is constant. Use the principle of virtual work.

F9–18. Solve Prob. F9–17 using Castigliano’s theorem.

F9–23. Determine the displacement at point C. EI is

constant. Use the principle of virtual work.

F9–24. Solve Prob. F9–23 using Castigliano’s theorem.

F9–15/9–16

F9–17/9–18

F9–19/9–20

F9–21/9–22

F9–23/9–24

388 CHAPTER 9DEFLECTIONS USING ENERGY M ETHODS

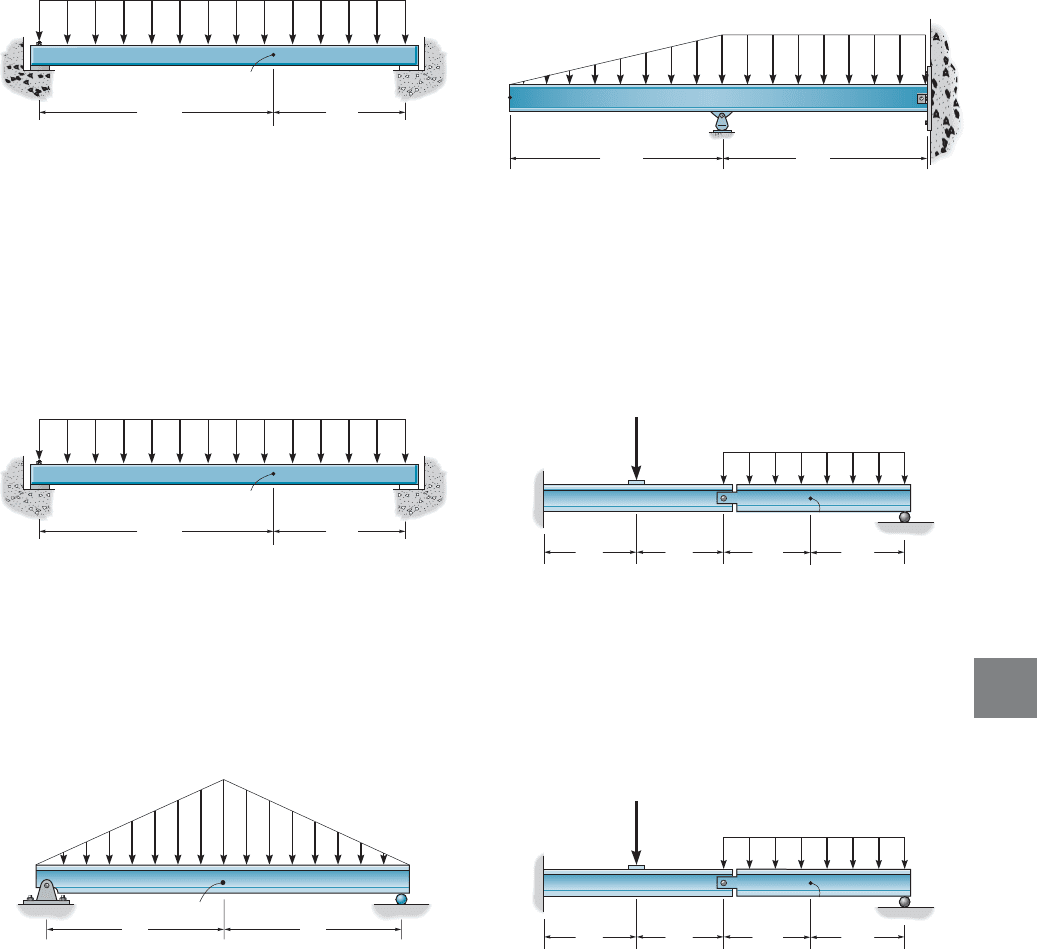
PROBLEMS

9–21. Determine the displacement of point C and the

slope at point B. EI is constant. Use the principle of virtual

work.

9–22. Solve Prob. 9–21 using Castigliano’s theorem.

9–29. Determine the slope and displacement at point C.

Use the method of virtual work. ksi,

9–30. Solve Prob. 9–29 using Castigliano’s theorem.

I = 800 in

E = 29(10

)

9–23. Determine the displacement at point C. EI is

constant. Use the method of virtual work.

*9–24. Solve Prob. 9–23 using Castigliano’s theorem.

9–31. Determine the displacement and slope at point C of

the cantilever beam.The moment of inertia of each segment

is indicated in the figure. Take . Use the

principle of virtual work.

*9–32. Solve Prob. 9–31 using Castigliano’s theorem.

E = 29(10

) ksi

9–33. Determine the slope and displacement at point B.

EI is constant. Use the method of virtual work.

9–34. Solve Prob. 9–33 using Castigliano’s theorem.

6 ft 6 ft

ABC

12 k

ft

6 k

ABC

6 ft

 500 in.

 200 in.

3 ft

50 kft

3 m

400 N

300 N/m

Probs. 9–21/9–22

Probs. 9–25/9–26/9–27/9–28

Probs. 9–23/9–24

Probs. 9–29/9–30

Probs. 9–31/9–32

Probs. 9–33/9–34

9–25. Determine the slope at point C. EI is constant. Use

the method of virtual work.

9–26. Solve Prob. 9–25 using Castigliano’s theorem.

9–27. Determine the slope at point A. EI is constant. Use

the method of virtual work.

*9–28. Solve Prob. 9–27 using Castigliano’s theorem.

9.9 CASTIGLIANO’S THEOREM FOR BEAMS AND FRAMES 389

9–35. Determine the slope and displacement at point B.

Assume the support at A is a pin and C is a roller. Take

Use the method of virtual work.

*9–36. Solve Prob. 9–35 using Castigliano’s theorem.

I = 300 in

.E = 29(10

) ksi,

*9–40. Determine the slope and displacement at point A.

Assume C is pinned. Use the principle of virtual work. EI is

constant.

9–41. Solve Prob. 9–40 using Castigliano’s theorem.

9–38. Determine the displacement of point C. Use the

method of virtual work. EI is constant.

9–39. Solve Prob. 9–38 using Castigliano’s theorem.

9–42. Determine the displacement at point D. Use the

principle of virtual work. EI is constant.

4 k/ft

10 ft 5 ft

6 kN/m

3 m 3 m

8 k

4 ft4 ft

3 k/ft

4 ft

Prob. 9–37

4 k/ft

10 ft 5 ft

Probs. 9–35/9–36

Probs. 9–38/9–39

Probs. 9–40/9–41

Prob. 9–43

8 k

4 ft4 ft

3 k/ft

4 ft

Prob. 9–42

9–37. Determine the slope and displacement at point B.

Assume the support at A is a pin and C is a roller. Account

for the additional strain energy due to shear. Take

, , and assume

AB has a cross-sectional area of . Use the

method of virtual work.

A = 7.50 in

G = 12(10

) ksi,I = 300 in

E = 29(10

) ksi

9–43. Determine the displacement at point D. Use

Castigliano’s theorem. EI is constant.