Hammond C. The Basics of Crystallography and Diffraction

Подождите немного. Документ загружается.

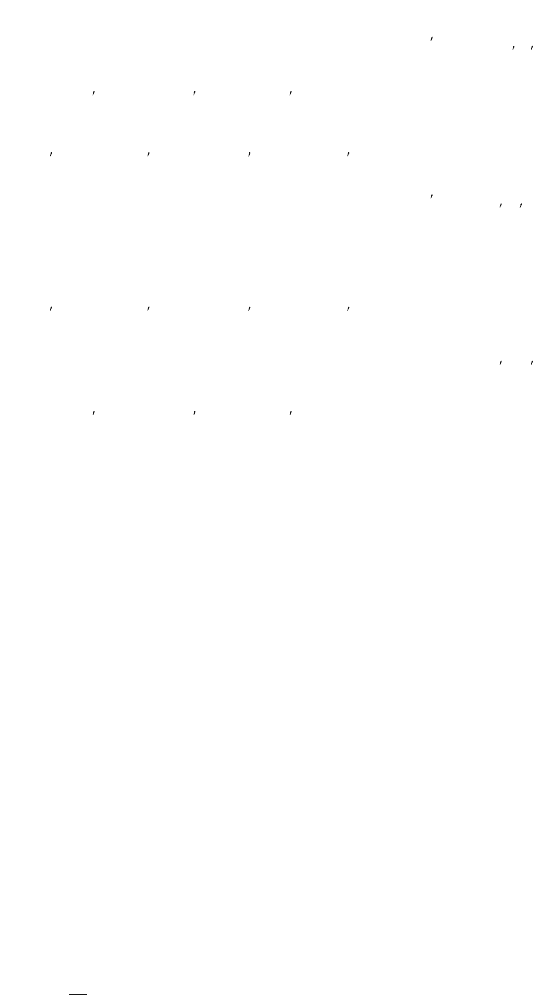
404 Answers to exercises

222

2 2 2

mm m m

m m m

m m m m

p m g 2

p m

g 2

Fig. E2.8.

Chapter 4

4.2

Structure Bravais lattice Motif

NaCl Cubic F (Na and Cl)

CsCl Cubic P (Cs and Cl)

Diamond Cubic F (C and C)

ZnS (sphalerite) Cubic F (Zn and S)

Zns (wurtzite) Hexagonal P (2Zn and 2S)

O (or CaF

) Cubic F (2Li and 1O)

CaTiO

Cubic P (1Ca, 1Ti, and 3O).

NB: in ferroelectric crystals the distortions which occur at the

Curie temperature and below change the Bravais lattice from

Cubic P to Tetragonal P to Orthorhombic P and to Rhombohe-

dral with decreasing temperature.

Chapter 5

5.1 In fcc crystals the slip planes are {111}, slip directions are



110



In bcc crystals the slip planes are {110}, slip directions are



111



5.2 [23

1], i.e. 2.1 +3.1 +

1.5 = 0.

(321), i.e. 3.1 +2.

1 +1.

1 = 0.

5.3 Triclinic, none; monoclinic, (010) and [010]; tetragonal, (001) and [001]; (hk0) and [hk0].

5.4 (4

1); (

31); [

1211

4]; [3

31] (or, their opposites, e.g. (

411), etc.).

5.5 (a) d

101

= 375 pm; d

100

= 452 pm; d

111

= 302 pm; d

202

= 188 pm.

(b) α = 48.1

◦

; β = 53.5

◦

; γ = 63.4

◦

Answers to exercises 405

◦

; q = 58.0

◦

; r = 45.3

◦

α, β, γ are not identical to p, q, r because the (111) plane normal is not parallel to the [111]

direction in orthorhombic crystals. These directions are only parallel in the case of cubic

crystals.

5.6 Writing planes as row matrices (Section 5.8);

Cubic I : (HKL)  (hkl)

⎛

⎜

⎝

⎞

⎟

⎠

Cubic F : (HKL)  (hkl)

⎛

⎜

⎝

⎞

⎟

⎠

The answers you obtain will depend upon your particular choices of A, B, C and a, b, c—but

they will be the same form as those given above. The reverse transformations for planes are

given by the inverse of the matrix in each case. Note that each matrix and its inverse also

gives the transformationfor direction symbols

[UVW ]  [uvw]

when these arewritten as

column matrices (seefor example, Section5.8). Finally, checkthat your determinantsare pos-

itive (

for Cubic I,

, for Cubic F in the examples above). A negative value means that you

have inadvertently chosen a left-handed axial system to describe one or other of the unit cells.

5.7 [001]=[0001]; [010]=[

10]; [210]=[30

30]=[10

10]; [110]=[11

20].

5.8 The direction [UVTW ]is[4

1] and the plane (hkil)is(1

1) (or their opposites).

5.9 Figure E5.9 showstracesof planes(0002), (10

11), etc. lying in the[

10]zone axis (normalto

the page). We require tan x = tan 60

◦

= c/a cos 30

◦

i.e. c/a = tan 60. cos 30 = 3/2 = 1.5.

(0002)

(1011)

[1210]

(1011)

(0002)

acos 30

Fig. E5.9.

406 Answers to exercises

Chapter 6

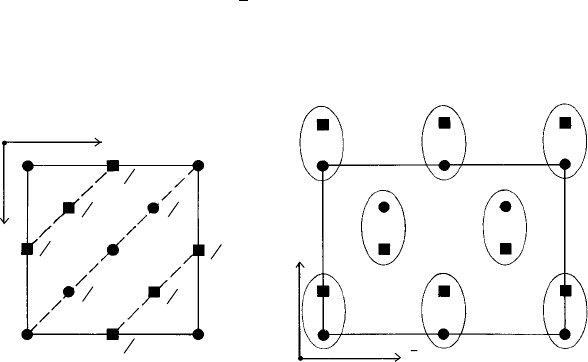
6.1 These reciprocal lattice sections all consist of hexagonal arrays of reciprocal lattice points,

those closest to the origin representing the {10

10} planes (hexagonal lattice), {110} planes

(cubic I lattice) and {220} planes (cubic F lattice).

6.2 Check your answers with the equations given in Appendix 4.

6.3 Yes.

6.4 r

∗

uvw



uvw



= 0.149Å

−1

Chapter 7

7.1 The unit cells of the net are ‘skew’, like that for the monoclinic crystal (Fig. 6.4(c)) or the

net (Fig. 7.1(d)). The (reciprocal lattice) unit cells of each twin orientation indicated by

circles and squares are shown in Fig. E7.1. The vertical row of spots through the origin

and perpendicular to the twin plane is common to both twin orientations and the spots are

unstreaked. Similarly, in every third row spots are common to both twin orientations and

are also unstreaked. This arises because one-in-three of the points in the net have the same

position, or are coincident in both twin orientations. Streaking, or the extension of the

reciprocal lattice points normal to the twin plane, increases as the twin thickness decreases,

except for those reciprocal lattice points common to both orientations.

7.2 The angles at which the second, fourth etc. maxima occur, i.e. 2(λ/a),4(λ/a), etc., coincide

with the angles at which the zero order, ﬁrst order etc. minima occur, i.e. (1λ/d ),2(λ/d ).

Hence alternate peaks or maxima in the diffraction pattern are missing.

Normal to twin plane

Twin related

unit cells

Coincident row of

spots for both

twin orientations

Fig. E7.1.

Chapter 8

8.1 α

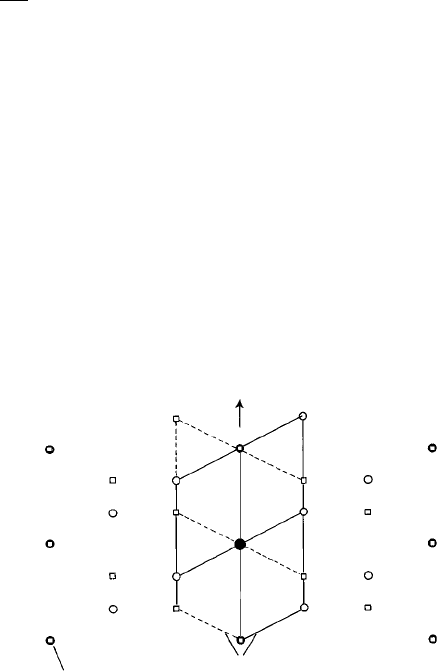
, the anglebetween thedirect anddiffracted beams, isequal to2θ (see Fig. E8.1); theplanes

are inclined to the diffraction grating such that they make equal angles with the incident

and reﬂected beams. Hence d

hki

= a cos θ . Substituting for θ and d

hki

in the equation

Answers to exercises 407

Reflected

beam

Diffraction

grating

Incident

beam

hkl

Reflecting

planes

Fig. E8.1.

(u + c)

(u – c)

hkl

Fig. E8.3.

nλ = a sin α

gives nλ = (d

hkl

/ cos θ)sin 2θ = (d

hkl

/ cos θ)2 cos θ sin θ = 2d

hkl

sin θ —

i.e. Bragg’s law.

8.2 d

110

= 0.2027 nm; d

200

= 0.1433 nm; and d

211

= 0.1170 nm. Planes whose d -spacings

are smaller than λ/2(= 0.1146 nm) do not satisfy Bragg’s law since the maximum possible

value of θ is 90

◦

8.3 Let the angle  and distance OB be as shown in Fig. E8.3. Then AB = OB sin(θ + ) and

BC = OB sin(θ − ). Summing and expanding the sine terms:

(AB +BC) = OB sin θ cos  +OB cos θ sin  + OB sin θ cos  −OB cos θ sin .

Hence, cancelling and substituting OB cos  = d

hkl

(AB +BC) = 2OB sin θ cos  = 2d

hkl

sin θ ;

i.e. the path difference is independent of the value of .

Chapter 9

9.1 Bragg’s law is satisﬁed for the planes (2

20), (3

10), (400), (310), (220) (in the hk0

section); (4

11), (4

1), (301), (411), (41

1) (in the hk1 and hk

1 sections) and (3

12),

408 Answers to exercises

2), (202), (20

2), (312), (31

2) (in the hk2 and hk

2 sections). The (larger) reﬂecting sphere

does not extend beyond the hk2 and hk

2 sections.

9.2 Bragg’s law is satisﬁed for the planes (420), (4

20), (220) and (2

20).

9.3 Let v be the root mean square velocity of the neutrons. Hence, the kinetic energy

3/2kT . The wavelength λ is given by de Broglie’s equation λ = h/mv = h/

√

3mkT.

Substituting the values of h, m, k and T = 373 K gives λ = 1.33 × 10

−10

m = 1.33Å.

9.4 The reﬂection condition for the cubic F lattice is h, k, l are all odd or all even and F

hkl

= 4f

(Appendix 6). For f we substitute the values for Zn and S, using the exponential form since

ZnS is non-centrosymmetric (point group

43m):

hkl

= 4



exp 2πi

(

h0 +k0 +l0

)

+ f

exp 2πi





= 4



+ f

exp πi

(

h +k + l

)



Hence, when

(

h +k + l

)

= 4n, F

hkl

= 4

(

+ f

)

(

h +k + l

)

= 4n + 2, F

hkl

= 4

(

− f

)

(

h +k + l

)

= 2n + 1, F

hkl

= 4

(

± if

)

9.5 For the origin at the centre of symmetry the atomic coordinates are ± (

), hence

hkl

= 4 ·2f

cos 2π





= 8f

cos π/4

(

h +k + l

)

which gives the condition that when

(h +k + l) = 4n +2, F

hkl

= 0

in addition to the condition for a cubic F lattice that F

hkl

= 0 when h, k, l are mixed (see

Table A6.2).

9.6 For f we substitute the values for f

at (000) and f

at (

0 0) (equivalent to (0

0) or

(0 0

)).

hkl

= 4



exp 2πi

(

h0 +k0 +l0

)

+ f

exp 2πi



+ l0 +k0



= 4

(

+ f

exp πih

)

Hence when h, k, l all odd F

hkl

= 4(f

− f

)

when h, k, l all even F

hkl

= 4(f

+ f

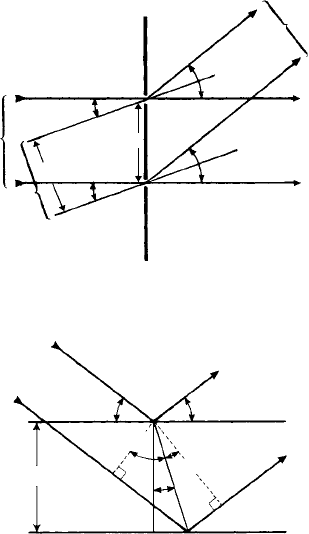
9.7 Simply measure the distances, r,ofthehk1 and hk2 layer lines from the hk0 layer line.

Figure E9.7 shows the Ewald sphere. The hk0, hk1, hk2, etc. reﬂections lie in the layer lines,

spacing c* as indicated, where

∗

= c, the lattice repeat distance.

From Fig. 9.7, tan 2θ = r/30 mm and sin 2θ =



∗



= λ/c

For the hk1 layer line r (corrected for scale factor) = 9.1 mm, whence c = 5.31Å.

For the hk2 layer line r (corrected for scale factor) = 21.3 mm, whence c/2 = 2.66Å, c =

5.32Å.

Answers to exercises 409

hk2 layer line

on film

hk2

hk1

hk0

C/C

rotation axis

hk1 layer line

on film

hk0 layer line

Exit hole

in film

Ewald reflecting

sphere

30mm

Fig. E9.7.

Chapter 10

10.4 The rings in both Figs 10.11(a) and (b) have the same diameters and hence show the same

sequence of d -spacings. The diameters of the rings represent a 4θ(not 2θ) angle, hence

tan2θ = radius of ring/specimen ﬁlm distance, from which, and using Bragg’s law, the d -

spacings can be determined. Referring to the table, the sequence of indices is (110), (040),

(130) (the ﬁrst three strong reﬂections in the zero layer-line in Fig. 10.11(b)), (111), (131)

(the weaker reﬂections in the ﬁrst layer-lines above and below) and (022), (112) (the very

faint reﬂections in the second layer lines).

Since the reﬂections in the zero layer-line are all of type {hk0}, they have a common

zone axis [001] which is parallel to the tensile axis and the direction of the polymer chains.

10.5 The 2θ angles and d-spacings of the peaks in (a) should ﬁrst be checked to conﬁrm that they

correspond to the 110, 200 and 211 reﬂections for α-Fe (a = 2.866Å). The half-height peak

widths (measurable only to a limited accuracy) give β(= β

obs

− β

inst

) values ≈ 0.004,

0.006 and 0.008 respectively which give residual stress values (σ =

E cot θ )inthe

range 1.10 ∼ 0.92 GPa. These are considerably greater than the yield stress of mild steel

indicating that a large component of the broadening arises from a reduction in crystallite

size.

10.6 The β values for the peaks are determined in the same way as for Exercise 10.5. Substituting

these values into the Scherrer equation β = λ/t cos θ gives grain size (t) values in the range

35–50 nm. Notice also the small peak shifts; these arise from variations in the α lattice

parameters as a result of a change in vanadium concentration following precipitation of the

vanadium-rich β phase.

Chapter 11

11.1 The equation to be derived follows from the discussion in Section 11.1. Since eV =

then

√

2meV = mv. Substituting in de Broglie’s equation gives λ = h/

√

2meV . The

numerical values obtained by substituting the m, e and V values are 10 kV: 12.2 pm

(12.2 pm); 100 kV: 3.88 pm (3.70 pm); 1 MV: 1.22 pm (0.87 pm). The relativistically

corrected values are in brackets, from which it is seen that the differences between the

values are insigniﬁcant at 10 kV, signiﬁcant at 100 kV and very signiﬁcant at 1 MV.

410 Answers to exercises

11.2 The zone axis of the pattern is



112



. The particular variant obtained depends upon the

variants of the indices chosen to index the pattern consistently.

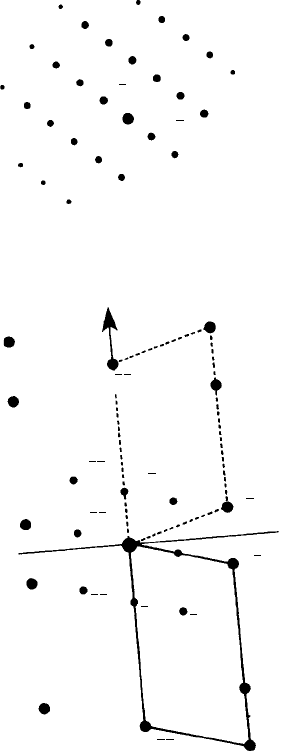
11.3 This problem is essentially the same as that for the simple cubic crystal as shown in Figs

11.1 and 11.2, except that the cubic P reciprocal lattice is replaced by the cubic F reciprocal

lattice (for a cubic I crystal—see Section 6.4). In the ZOLZ 0kl and FOLZ 1kl the reﬂecting

planes are those for which (h +k + I ) = an even number (see Fig. 6.8(a)).

11.4 The diffraction pattern is from Fe

C (cementite) and is indexed in Fig. E11.4. Notice that

the pattern is not rectangular, but slightly skew. Since the structure is orthorhombic the

order of the indices hkl may not be changed; only their signs may be changed, e.g. the

allowed permutations of 103 are:

103, 10

3, 103,



103

112

121

130

000

011

Fig. E11.4.

112

103

Twin plane normal

112

//112

112

//112

011

110

Trace of

twin plane

101

110

112

101

011

103

Fig. E11.6.

Answers to exercises 411

11.5 In Fig. 11.6 the camera constant λL = 27Å mm.

11.6 The diffraction patterns may be indexed as shown in Fig. E11.6. The ‘matrix’α-Fe orienta-

tion is outlined by solid lines and the twin orientation by dashed lines. The trace of the twin

plane and the twin plane normal are indicated (compare with the twin-related unit cells in

the optical diffraction pattern as shown in the answer to Exercise 7.1). The reﬂections for

matrix (m) and twin (t) orientations are indexed such that (e.g.) 0

is related to 0

by reﬂection in the twin plane. The Fe

C reﬂections may be indexed as shown, giving the

orientation relationship between the α-Fe (matrix) and Fe

C as:

(011)



11)

α−Fe

and (

101)



(112)

α−Fe

For the zone axes, obtained by cross multiplication (see Section 5.6.2):



α−Fe

11.7 Figure E11.7(a) shows a [001] projection of the diamond-cubic structure and the traces

(dashed lines) of the (220) planes, the atoms in successive planes being denoted by the

• and  symbols; separation =

√

3/4 (0.566 nm) = 0.245 nm. Figure E11.7(b) shows

the 110 projection and the ‘dumbbell’ (circled) pattern of atoms; spacing (in projection)

= 1/4(0.566nm) = 0.142 nm. Note: Fig. E11.7(b) rotated 90

◦

with respect to Fig. 11.15.

[001]

(a) (b)

[010]

[001]

[100]

[110]

[100]

Fig. E11.7.

Chapter 12

12.1 Figure E12.1 shows a ‘vertical’ section with the axis of the cone of elliptical cross-section

marked OS as in Fig. 12.3(a) and at angle x to the N–S direction. The tangent to the circle

(heavy line), which is parallel to the small circle on the sphere, is also tilted at this angle x to

the axis of the cone since the angle at the centre of the circle is 2x (Euclid, Proposition 20,

p. 201). Since the two circular sections must, by symmetry, be inclined at equal and opposite

angles to the axis of the cone OS, then the other circular section, indicated by the other

heavy line, is parallel to the plane of the stereographic projection.

412 Answers to exercises

Tangent to circle

Traces of circular

sections of cone

Plane of

projection

Axis of cone

Fig. E12.1.

12.2 The α, β and γ angles of the (212) plane to the x, y and z axes are 48

◦

,71

◦

and 48

◦

, hence

the direction cosines cos α, cos β and cos γ are 0.67, 0.33 and 0.67. The ratios between

these direction cosines are equal to the ratios between the Miller indices, i.e. 2:1:2. The α,

β and γ angles of the (

32) plane are −50

◦

, −50

◦

and 65

◦

; hence the direction cosines are

−0.64, −0.64, 0.42 which are equal to the ratios

3:2.

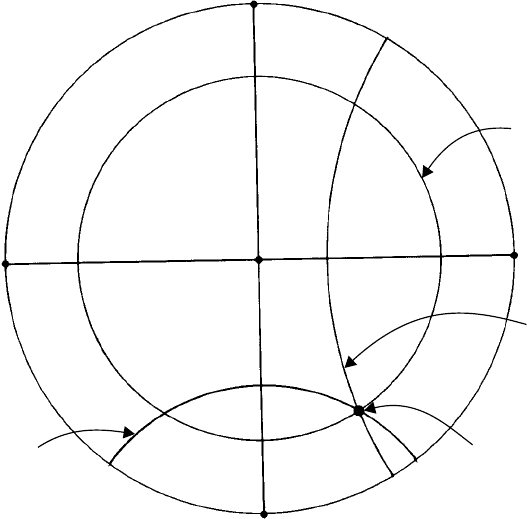
12.3 For plane A, using the Wulff net with its axis A…A along the x-axis, draw in the small

circle 36.5

◦

from the +x-axis; this small circle represents the locus of all planes which lie

36.5

◦

from the +x-axis. Now rotate the Wulff net 90

◦

so that its axis A…A lies along the

y-axis and draw in the small circle 57.5

◦

from the +y-axis. The two points of intersection of

the small circles both in the northern and southern hemispheres (i.e. above and below the

plane of projection) show the two possible positions of plane A. Finally, draw in the small

circle (the ‘line of latitude’) at 74.5

◦

from the +z-axis. The three small circles all intersect

at the point in the northern hemisphere and hence give the position of plane A (see Fig.

E12.3).

The position of plane B is found by the same procedure except that a−sign indicates

that the small circle is drawn from the−(minus)-axis.

Answers to exercises 413

–

Small circle

74.5° from

+ -axis

Small circle

57.5° from

+ -axis

Pole of plane A

Small circle

36.5° from

+ -axis

–y

Fig. E12.3.

To ﬁnd the Miller indicesof planesAand B,write downthe direction cosines of theangles

to the x, y and z-axes respectively and express these as the ratios of whole numbers, i.e.

Plane A +36.5

◦

+57.5

◦

+74.5

◦

direction cosines: +0.804 : +0.537 : +0.267

ratios: 3 : 2 : 1

Hence the Miller index of plane A is (321).

Similarly, the Miller index of plane B is (

12).

The angles between the planes are found by rotating the Wulff net until each pair of planes

lie in the same great circle.

Plane A and planeB:121

◦

Plane A and (

11) : 126

◦

Plane B and (101) : 90

◦

Plane B and (

101) :19

◦