Hager G., Wellein G. Introduction to High Performance Computing for Scientists and Engineers

Подождите немного. Документ загружается.

Solutions to the problems 295

1 double precision, dimension(0:255), save :: vtab

2 double precision, dimension(N) :: ftab

3 logical, save :: flag = .TRUE.

4 if(flag) then ! do this only once

5 flag = .FALSE.

6 do i=0,255

7 vtab(i) = -0.5d0

COS(2.d0

DBLE(i))

8 enddo

9 endif

10 do i=1,N ! do this on every call

11 ftab(i) = vtab(IAND(v(i),255))

12 enddo

13 do j=1,N

14 do i=1,N

15 mat(i,j) = s(i,j)

ftab(i)

16 enddo

17 enddo

Since v() may change between calls of the function, ftab() must be recomputed

every time, but the inner loop is now trivially SIMD-vectorizable.

Solution 3.8 (page 93): TLB impact.

TLB “cache lines” are memory pages, so the penalty for a miss must be compared

to the time it takes to stream one page into cache. At present, memory bandwidth

is a few GBytes/sec per core, leading to a transfer time of around 1

s for a 4kB

page. The penalty for a TLB miss varies widely across architectures, but it is usually

far smaller than 100 CPU cycles. At clock frequencies of around 2 GHz, one TLB

miss per page on a pure streaming code has no noticeable impact on performance. If

signiﬁcantly less than a page is transferred before going to the next, this will change,

of course.

Some systems have larger memory pages, or can be conﬁgured to use them. At

best, the complete working set of an application can be mapped by the TLB, so that

the number of misses is zero. Even if this is not the case, large pages can enhance the

probability of TLB hits, because it becomes less likely that a new page is hit at any

given moment. However, switching to large pages also usually reduces the number

of available TLB entries.

Solution 4.1 (page 114): Building fat-tree network hierarchies.

Static routing assigns a ﬁxed network route to each pair of communication part-

ners. With a 2:3 oversubscription, some connections will get less bandwidth into the

spine because it is not possible to distribute the leaves evenly among the spine con-

nections (the number of leaves on a leaf switch is not a multiple of the number of its

connections into the spine). Hence, the network gets even more unbalanced, beyond

the contention effects incurred by static routing and oversubscription alone.

296 Introduction to High Performance Computing for Scientists and Engineers

Solution 5.1 (page 140): Overlapping communication and computation.

Hiding communication behind computation is something that sounds straightfor-

ward but is usually not easy to achieve in practice; see Sections 10.4.3 and 11.1.3 for

details. Anyway, assuming that it is possible, the time for parallel execution in the

denominator of the strong scaling speedup function (5.30) becomes

max

(1−s)/N,



−



−1

. (B.1)

This describes a crossover from perfectly to partially hidden communication when

(1−s) =

1−

. (B.2)

As the right-hand side of this equation is strictly monotonous in N

if 0 ≤

≤ 1,

the crossover will always be shifted to larger N on the slow computer (

> 1). By

how much exactly (a factor of at least

is certainly desirable) is given by the ratio

(

)/N

(

= 1), but solving for N

is not easily possible. Fortunately, it is sufﬁcient

to investigate the important limits

= 0 and

= 0. For vanishing latency,

(

= 0) =



(1−s)



1/(1−

)

, (B.3)

and

(

> 1)

(

= 1)



1/(1−

)

. (B.4)

In the latency-dominated limit

= 0 we immediately get

(

> 1)

(

= 1)



. (B.5)

We have derived an additional beneﬁt of slow computers: If communication can be

hidden behind computation, it becomes noticeable at a certain N, which is at least

times larger than on the standard computer.

Can you do the same analysis for weak scaling?

Solution 5.2 (page 141): Choosing an optimal number of workers.

For strong scaling and latency-dominated communication, the walltime for exe-

cution (“time to solution”) is

= s+

1−s

(B.6)

if s is the nonparallelizable fraction and

is the latency. The cost for using N pro-

cessors for a time T

is NT

, yielding a cost-walltime product of

V = NT

= N



1−s



, (B.7)

Solutions to the problems 297

which is extremal if

∂

[(1+

N + (N −1)s)(s−1+ N(

+ s))] = 0 . (B.8)

The only positive solution of this equation in N is

opt

1−s

+ s

. (B.9)

Interestingly, if we assume two-dimensional domain decomposition with halo ex-

change so that

= s+

1−s

−1/2

, (B.10)

the result is the same as in (B.9), i.e., independent of

. This is a special case, how-

ever; any other power of N in the communication overhead leads to substantially

different results (and a much more complex derivation).

Finally, the speedup obtained at N = N

opt

2(s+

) +

+ s

1−s

−1

. (B.11)

A comparison with the maximum speedup S

max

= 1/(

+ s) yields

max

opt

= 2+

(1−s)(

+ s)

, (B.12)

so for

= 0 the “sweet spot” lies at half the maximum speedup, and even lower for

ﬁnite

Of course, no matter what the parallel application’s communication requirements

are, if the workload is such that the time for a single serial application run is “toler-

able,” and many such runs must be conducted, the most efﬁcient way to use a par-

allel computer is throughput mode. In throughput mode, many instances of a serial

code are run concurrently under control of a resource management system (which

is present on all production machines). This provides the best utilization of all re-

sources. For obvious reasons, such a workload is not suitable for massively parallel

machines with expensive interconnect networks.

Solution 5.3 (page 141): The impact of synchronization.

Synchronization appears at the same place as communication overhead, leading

to eventual slowdown with strong scaling. For weak scaling, linear scalability is de-

stroyed; linear sync overhead even leads to saturation.

Solution 5.4 (page 141): Accelerator devices.

Ignoring communication aspects (e.g., overhead for moving data into and out of

the accelerator), we can model the situation by assuming that the accelerated parts

298 Introduction to High Performance Computing for Scientists and Engineers

of the application execute

times faster than on the host, whereas the rest stays

unchanged. Using Amdahl’s Law, s is the host part and p = 1−s is the accelerated

part. Therefore, the asymptotic performance is governed by thehost part; if, e.g.,

100 and s = 10

−2

, the speedup is only 50, and we are wasting half of the accelerator’s

capability. To get a speedup of r

with 0 < r < 1, we need to solve

1−s

= r

(B.13)

for s, leading to

s =

−1

, (B.14)

which yields s ≈ 1.1 ×10

−3

at r = 0.9 and

= 100. The lesson is that efﬁcient

use of accelerators requires a major part of original execution time (much more than

just 1 −1/

) to be moved to special hardware. Incidentally, Amdahl had formu-

lated his famous law in his original paper along the lines of “accelerated execu-

tion” versus “housekeeping and data management” effort on the ILLIAC IV super-

computer [R40], which implemented a massively data-parallel SIMD programming

model:

A fairly obvious conclusion which can be drawn at this point is that the effort

expended on achieving high parallel processing rates is wasted unless it is ac-

companied by achievements in sequential processing rates of very nearly the

same magnitude. [M45]

This statement ﬁts perfectly to the situation described above. In essence, it was al-

ready derived mathematically in Section 5.3.5, albeit in a slightly different context.

One may argue that enlarging the (accelerated) problem size would mitigate the

problem, but this is debatable because of the memory size restrictions on accelerator

hardware. The larger the performance of a computational unit (core, socket, node,

accelerator), the larger its memory must be to keep the serial (or unaccelerated) part

and communication overhead under control.

Solution 6.1 (page 162): OpenMP correctness.

The variable noise in subroutine f() carries an implicit SAVE attribute, be-

cause it is initialized on declaration. Its initial value will thus only be set on the ﬁrst

call, which is exactly what would be intended if the code were serial. However, call-

ing f() from a parallel region makes noise a shared variable, and there will be

a race condition. To correct this problem, either noise should be provided as an

argument to f() (similar to the seed in thread safe random number generators), or

its update should be protected via a synchronization construct.

Solution 6.2 (page 162):

by Monte Carlo.

The key ingredient is a thread safe random number generator. According to the

OpenMP standard [P11], the RANDOM_NUMBER() intrinsic subroutine in Fortran 90

Solutions to the problems 299

is supposed to be thread safe, so it could be used here. However, there are perfor-

mance implications (why?), and it is usually better to avoid built-in generators any-

way (see, e.g., [N51] for a thorough discussion), so we just assume that there is a

function ran_gen(), which essentially behaves like the rand_r() function from

POSIX: It takes a reference to an integer random seed, which is updated on each call

and stored in the calling function, separately for each thread. The function returns an

integer between 0 and 2

, which is easily converted to a ﬂoating-point number in

the required range:

1 integer(kind=8) :: sum

2 integer, parameter :: ITER = 1000000000

3 integer :: seed, i

4 double precision, parameter :: rcp = 1.d0/2

5 double precision :: x,y,pi

6 !$OMP PARALLEL PRIVATE(x,y,seed) REDUCTION(+:sum)

7 seed = omp_get_thread_num() ! everyone gets their own seed

8 !$OMP DO

9 do i=1,ITER

10 x = ran_gen(seed)

rcp

11 y = ran_gen(seed)

rcp

12 if (x

x + y

y .le. 1.d0) sum=sum+1

13 enddo

14 !$OMP END DO

15 !$OMP END PARALLEL

16 pi = (4.d0

sum) / ITER

In line 7, the threads’ private seeds are set to distinct values. The “hit count” for the

quarter circle in the ﬁrst quadrant is obtained from a reduction operation (summation

across all threads) in sum, and used in line 16 to compute the ﬁnal result for

Using different seeds for all threads is vital because if each thread produces the

same sequence of pseudorandom numbers, the statistical error would be the same as

if only a single thread were running.

Solution 6.3 (page 163): Disentangling critical regions.

Evaluation of func() does not have to be protected by a critical region at all (as

opposed to the update of sum). It can be done outside, and the two critical regions

will not interfere any more:

1 !$OMP PARALLEL DO PRIVATE(x)

2 do i=1,N

3 x = SIN(2

DBLE(i)/N)

4 x = func(x)

5 !$OMP CRITICAL

6 sum = sum + x

7 !$OMP END CRITICAL

8 enddo

9 !$OMP END PARALLEL DO

10 ...

11 double precision FUNCTION func(v)

12 double precision :: v

13 !$OMP CRITICAL

300 Introduction to High Performance Computing for Scientists and Engineers

14 func = v + random_func()

15 !$OMP END CRITICAL

16 END SUBROUTINE func

Solution 6.4 (page 163): Synchronization perils.

A barrier must always be encountered by all threads in the team. This is not

guaranteed in a workshared loop.

Solution 6.5 (page 163): Unparallelizable?

Thanks to Jakub Jelinek from Red Hat for providing this solution. Clearly, the

loop can be parallelized right away if we realize that opt(n)=up

n, but expo-

nentiation is so expensive that we’d rather not take this route (although scalability

will be great if we take the single-thread performance of the parallel code as a base-

line [S7]). Instead we revert to the original (fast) version for calculating opt(n) if

we are sure that the previous iteration handled by this thread was at n-1 (line 12).

On the other hand, if we are at the start of a new chunk, indices were skipped and

opt(n) must be calculated by exponentiation (line 14):

1 double precision, parameter :: up = 1.00001d0

2 double precision :: Sn, origSn

3 double precision, dimension(0:len) :: opt

4 integer :: n, lastn

6 origSn = 1.d0

7 lastn = -2

9 !$OMP PARALLEL DO FIRSTPRIVATE(lastn) LASTPRIVATE(Sn)

10 do n = 0,len

11 if(lastn .eq. n-1) then ! still in same chunk?

12 Sn = Sn

up ! yes: fast version

13 else

14 Sn = origSn

n ! no: slow version

15 endif

16 opt(n) = Sn

17 lastn = n ! storing index

18 enddo

19 !$OMP END PARALLEL DO

20 Sn = Sn

The LASTPRIVATE(Sn) clause ensures that Sn has the same value as in the serial

case after the loop is ﬁnished. FIRSTPRIVATE(lastn) assigns the initial value of

lastn to its private copies when the parallel region starts. This is purely for conve-

nience, because we could have done the copying manually by splitting the combined

PARALLEL DO directive.

While the solution works for all OpenMP loop scheduling options, it will be

especially slow for static or dynamic scheduling with small chunksizes. In the special

case of “STATIC,1” it will be just as slow as using exponentiation from the start.

Solutions to the problems 301

Solution 6.6 (page 163): Gauss–Seidel pipelined.

This optimization is also called loop skewing. Starting with a particular site, all

sites that can be updated at the same time are part of a so-calledhyperplane and fulﬁll

the condition i+ j+k = const. = 3n, with n ≥1. Pipelined execution is now possible

as all inner loop iterations are independent, enabling efﬁcient use of vector pipes

(see Section 1.6). Cache-based processors, however, suffer from the erratic access

patterns generated by the hyperplane method. Cache lines once fetched for a certain

stencil update do not stay in cache long enough to exploit spatial locality. Bandwidth

utilization (as seen from the application) is thus very poor. This is why the standard

formulation of the Gauss–Seidel loop nest together with wavefront parallelization

is preferable for cache-based microprocessors, despite the performance loss from

insufﬁcient pipelining.

Solution 7.1 (page 184): Privatization gymnastics.

In C/C++, reduction clauses cannot be applied to arrays. The reduction must

thus be done manually. A firstprivate clause helps with initializing the private

copies of s[]; in a “true” OpenMP reduction, this would be automatic as well:

1 int s[8] = {0};

2 int

ps = s;

4 #pragma omp parallel firstprivate(s)

5 {

6 #pragma omp for

7 for(int i=0; i<N; ++i)

8 s[a[i]]++;

9 #ifdef _OPENMP

10 #pragma omp critical

11 {

12 for(int i=0; i<8; ++i) { // reduction loop

13 ps[i] += s[i];

14 }

15 } // end critical

16 #endif

17 } // end parallel

Using conditional compilation, we skip the explicit reduction if the code is compiled

without OpenMP.

Similar measures must be taken even in Fortran if the reduction operator to be

used is not supported directly by OpenMP. Likewise, overloaded C++ operators are

not allowed in reduction clauses even on scalar types.

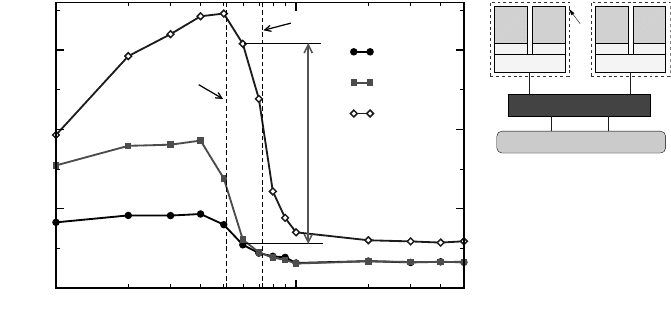
Solution 7.2 (page 184): Superlinear speedup.

Figure B.2 shows that the described situation occurs at a problem size around

600

: A single 4MB L2 cache is too small to accommodate the working set, but

8MB is sufﬁcient. The speedup when going from one (or two) threads to four is 5.4.

When the working set ﬁts into cache, the grid updates are so fast that typical

302 Introduction to High Performance Computing for Scientists and Engineers

100 1000

500

1000

1500

Performance [MLUPs/sec]

1 thread

2 threads

1 socket

4 threads

8 MB L2

4 MB L2

5.4x speedup

socket

32k L1D 32k L1D 32k L1D 32k L1D

Chipset

Memory

P P P P

4MB L2 4MB L2

Figure B.2: Superlinear speedup with the 2D Jacobi solver (same data as in Figure 6.3). At

a problem size of 600

, the working set is too large to ﬁt into one socket’s L2 cache, so

performance is close to memory-bound (ﬁlled symbols). Using two additional threads (open

diamonds), 8MB cache become available, which is large enough to accommodate all data.

Hence, the 5.4× speedup.

OpenMP overhead, especially implicit barriers (see Section 7.2.2), might dominate

runtime if the number of threads is large. To ﬁnd a criterion for this we must com-

pare the time for one sweep with a typical synchronization overhead. Looking at

the maximum two-thread in-cache performance (ﬁlled squares), we estimate that a

single sweep takes about 170

s. As a very rough guideline we may assume that syn-

chronizing all threads in a shared-memory machine requires about 1

s per socket if

the barrier is implemented efﬁciently [M41]. Hence, on standard two- or four-socket

nodes one should be able to observe superlinear scaling for this kind of problem.

Solution 7.3 (page 184): Reductions and initial values.

If the code is compiled without OpenMP support, it should still produce correct

results, which it doesn’t if R is not initialized. If we could use C(j) as a reduction

variable, this detour would not be necessary, but only named variables are allowed in

reduction clauses.

Solution 7.4 (page 184): Optimal thread count.

Parallelism adds overhead, so one should use as few threads as possible. The

optimal number is given by the scalability of main memory bandwidth versus thread

count. If two out of six threads already saturate a socket’s memory bus, running more

than four threads does not make sense. All the details about cache groups and system

architecture are much less relevant.

Note that shared caches often do not provide perfect bandwidth scaling as well,

so this reasoning may apply to in-cache computations, too [M41].

Solutions to the problems 303

Solution 8.1 (page 201): Dynamic scheduling and ccNUMA.

As usual, performance (P) is work (W) divided by time (t). We choose W = 2,

meaning that two memory pages are to be assigned to the two running threads. Each

chunk takes a duration of t = 1 to execute locally, so that P = 2p if there is no

nonlocal access. In general, four cases must be distinguished:

1. Both threads access their page locally: t = 1.

2. Both threads have to access their page remotely: Since the inter-LD network is

assumed to be inﬁnitely fast, and there is no contention on either memory bus,

we have t = 1.

3. Both threads access their page in LD0: Contention on this memory bus leads

to t = 2.

4. Both threads access their page in LD1: Contention on this memory bus leads

to t = 2.

These four cases occur with equal probability, so the average time to stream the two

pages is t

avg

= (1 + 1 + 2+ 2)/4 = 1.5. Hence, P = W/t

avg

= 4p/3, i.e., the code

runs 33% slower than with perfect access locality.

This derivation is so simple because we deal with only two locality domains, and

the elementary work package is two pages no matter where they are mapped. Can

you generalize the analysis to an arbitrary number of locality domains?

Solution 8.2 (page 202): Unfortunate chunksizes.

There are two possible reasons for bad performance at small chunksizes:

• This is a situation in which the hardware-based prefetching mechanisms of

x86-based processors are actually counterproductive. Once activated by a num-

ber of successive cache misses (two in this case), the prefetcher starts transfer-

ring data to cache until the end of the current page is reached (or until can-

celed). If the chunksize is smaller than a page, some of this data is not needed

and will only waste bandwidth and cache capacity. The closer the chunksize

gets to the page size, the smaller this effect.

• A small chunksize will also increase the number of TLB misses. The actual

performance impact of TLB misses is strongly processor-dependent. See also

Problem 3.8.

Solution 8.3 (page 202): Speeding up “small” jobs.

If multiple streams are required, round-robin placement may yield better single-

socket performance than ﬁrst touch because part of the bandwidth can be satisﬁed

via remote accesses. The possible beneﬁt of this strategy depends strongly on the

hardware, though.

304 Introduction to High Performance Computing for Scientists and Engineers

Solution 8.4 (page 202): Triangular matrix-vector multiplication.

Parallelizing the inner reduction loop would be ﬁne, but will only work with very

large problems because of OpenMP overhead and NUMA placement problems. The

outer loop, however, has different workloads for different iterations, so there is a

severe load balancing problem:

1 !$OMP PARALLEL DO SCHEDULE(RUNTIME)

2 do r=1,N ! parallel initialization

3 y(r) = 0.d0

4 x(r) = 0.d0

5 do c=1,r

6 a(c,r) =0.d0

7 enddo

8 enddo

9 !$OMP END PARALLEL DO

10 ...

11 !$OMP PARALLEL DO SCHEDULE(RUNTIME)

12 do r=1,N ! actual triangular MVM loop

13 do c=1,r

14 y(r) = y(r) + a(c,r)

x(c)

15 enddo

16 enddo

17 !$OMP END PARALLEL DO

We have added the parallel initialization loop for good page placement in ccNUMA

systems.

Standard static scheduling is certainly not a good choice here.Guided or dynamic

scheduling with an appropriate chunksize could balance the load without too much

overhead, but leads to nonlocal accesses on ccNUMA because chunks are assigned

dynamically at runtime. Hence, the only reasonable alternative is static scheduling,

and a chunksize that enables proper NUMA placement at least for matrix rows that

are not too close to the “tip” of the triangle.

What about the placement issues for x()?

Solution 8.5 (page 202): NUMA placement by overloading.

The parallel loop schedule is the crucial point. The loop schedules of the ini-

tialization and worksharing loops should be identical. Had we used a single loop, a

possible chunksize would be interpreted as a multiple of one loop iteration, which

touches a single char. A chunksize on a worksharing loop handling objects of type

D would refer to units of sizeof(D), and NUMA placement would be wrong.

Solution 9.1 (page 233): Shifts and deadlocks.

Exchanging the order of sends and receives also works with an odd number of

processes. The “leftover” process will just have to wait until its direct neighbors have

ﬁnished communicating. See Section 10.3.1 for a discussion of the “open chain”

case.