Громов Ю.Ю. Фрактальный анализ и процессы в компьютерных сетях
Подождите немного. Документ загружается.

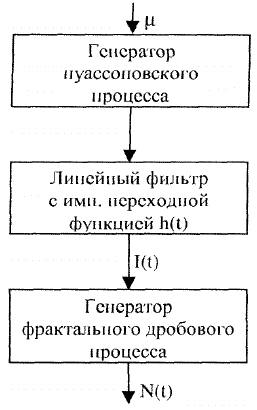
Рис. 3.4. Этапы формирования фрактального дробового
точечного процесса
Этот фильтр порождает модулирующий сигнал I(t), с помощью которого формируется на заключительном этапе фрак-
тальный дробовый точечный процесс. Импульсная переходная функция вида (3.57) ранее в разд. 2 рассматривалась при ис-
следовании дробного интеграла. Последний является модификацией известного из теории линейных систем интеграла
свертки, описывающего выходной сигнал системы, но функционирующей, как уже было ранее отмечено, только на части
своих состояний. В качестве воздействующего процесса используется стационарный импульсный пуассоновский процесс
ξ(t) (3.12) с интенсивностью µ. Упомянутый интеграл свертки записывается в форме
() ( ) ()
ττξτ−=
∫
dthtI
B
0
,
где область изменения аргумента рассматриваемых процессов 0 ≤ τ < B.
На основании уже используемой в разд. 3.3 теоремы Кембелла математическое ожидание и корреляционная функция
случайного сигнала с учетом области изменения аргумента соответственно равны:
() (){} ()
∫
µ=µ=λ==τ
B
I
adtthtIMk
0
1
; (3.58)
() ()( ){} ()()
∫
τ+µ=λ−τ+=τ
B
I
dtththtItIMk
0
2
. (3.59)
Математическое ожидание и корреляционная функция случайной интенсивности точечного процесса на основании
(3.58) и (3.59) с учетом (3.16) и (3.27) соответственно принимают вид:
akk
I
µ=
λ
=
=
11
; (3.60)
() () () () () ( )
∫
τ+µ+τλδ=τ+τλδ=τ
B
I
dtththkk
0
22
, (3.61)
где параметр
()
∫
α
−
−α
α==
B
BKdttKa
0
2/
1
12/
2/ .
Таким образом, выражение для интенсивности дробового точечного процесса – одного из фундаментальных парамет-
ров, равно
λ = Kµ(α/2)
–1
B
α/2
. (3.62)
Для определения другого фундаментального параметра Т
0
– начального времени установки, воспользуемся выражением
для фактора Фано
() ( ) ( ) ()
τττ−λ=
∫
−
dkTTTF
T
2
0
1
2 . (3.63)
Подставим в выражение (3.63) корреляционную функцию (3.61), с учетом (3.57) получаем
() ( ) ( ) ()( )
() ( )
()
∫∫
∫∫
τ−
−α
−
τ−
−
τ+ττ−λµ+=
=ττ−ττ−λµ+=
BT
BT
dtttdTKT
dththdTKTTF
0
12/
2
0
2
1
00
2
1
.21
21
(3.64)
Определим сначала внутренний интеграл, введя новую временную z = t/τ:
()
()
∫∫
τ−
τ
τ−
−α
−α−α
−α
+τ=τ+
B
B
dzzzdttt
00
12/
12/1
12/
2
.1 (3.65)
При В → ∞ интеграл (3.65) оказывается табличным. В результате при достаточно большом В получаем
()
()()
()
∫
τ−
−α−α
α−Γ
α−ΓαΓ
τ=τ+
B
dttt
0
112/2
2/1
12/
. (3.66)
После подстановки (3.66) в выражение (3.64) внешний интеграл с учетом новой переменной z = τ/T равен
()()
()
()
()()
()
()
()()
()( )
.
2/11
12/
1
2/1
12/
2/1
12/
1
1
0
11
0
α−Γ+αα
α−ΓαΓ
=
=−
α−Γ
α−ΓαΓ
=τττ−
α−Γ
α−ΓαΓ
+α
−α−α
∫∫
Т
dzzzdT
T
(3.67)
В результате подстановки соотношения (3.67) в (3.64) с учетом (3.60) получаем
()
()()
()( )
2/11
12/
1
2/
α−Γ+α
α−ΓαΓ
+=
αα−
TKBTF . (3.68)
Сравнивая (3.68) с фактором Фано (3.32), приходим к выражению детального времени установки
(
)( )
()()
α−ΓαΓ
α−Γ+α
=
α−α
12/
2/11
2/1
0
BKT . (3.69)
Параметры Т
0
(3.69) вместе с λ (3.62) и Н = (1 + α) / 2 образуют группу фундаментальных параметров сетевого трафика.
В полученных параметрах часть характеристик определяется однозначно, другие, как например, µ и В выбираются для
задания характеристик поведения трафика. Так, при малых значениях произведения µВ << 1 импульсная переходная функ-
ция перекрывается редко, и временные интервалы между пачками пакетов становятся существенно большими. При µВ >> 1
импульсная переходная функция перекрывается часто, и вероятность больших интервалов уменьшается.

4. МОДЕЛИРОВАНИЕ СЕТЕВОГО ТРАФИКА
ФРАКТАЛЬНЫМ БРОУНОВСКИМ ДВИЖЕНИЕМ
В приведенных ниже материалах рассматриваются статистики сетевых процессов, базирующиеся на свойствах непре-
рывного с вероятностью 1 фрактального броуновского движения. К числу исследуемых процессов отнесены модели ON/OFF
режима сетевого трафика и RTT-задержки. Прежде чем перейти к фрактальному броуновскому движению, обсудим свойства
классического броуновского движения.
4.1. КЛАССИЧЕСКОЕ БРОУНОВСКОЕ ДВИЖЕНИЕ
К модели классического броуновского движения – винеровскому процессу (процессу Винера или Винера – Леви) при-
ходят на основании следующих соображений. Частицы жидкости или газа в отсутствие внешних воздействий из-за столкно-
вений с молекулами находятся в постоянном хаотическом движении (броуновском движении), интенсивность которого зави-
сит от температуры и плотности среды. При этих столкновениях частицы изменяют свою скорость и направление движения.
Если масса частицы равна m, то, пренебрегая силами трения, скорость движения частицы B(t) по какой-либо координате на
основании закона Ньютона определяется из соотношения
(
)
()
tn
dt
tdB
m = ,
где функция n(t) является составляющей по этой координате случайной последовательности силовых толчков. Из условия
симметрии направления этих толчков равновероятны и поэтому математическое ожидание этой функции равно нулю:
M{n(t)} = 0.
При определении статистик броуновского движения необходимо исходить из того, что в реальном физическом экспе-
рименте время корреляции процесса n(t) конечно и, грубо говоря, не превосходит среднего времени между столкновениями
τ
0
. Далее необходимо иметь ввиду, что реальные физические приборы, осуществляющие наблюдения и измерения, имеют
конечное время разрешения ∆t. В течение этого времени при большой концентрации молекул частица испытывает большое
число столкновений, вследствие чего интервал измерения оказывается много больше интервала корреляции: ∆t >> τ
0
. В связи
с изложенным на основании центральной предельной теоремы процесс n(t) приближенно можно представить гауссовским
процессом с математическим ожиданием равным нулю и дельтаобразной корреляционной функцией (гауссовским белым
шумом). Винеровский процесс B(t) по определению находится через белый шум n(t) из стохастического дифференциального
уравнения
()
nt
dt
tdB
= , B(t
0
) = B
0
= 0 или
() () ()
ττ=τ=
∫∫
dndBtB
t
t
t
t
00
. (4.1)
Математическое ожидание и корреляционная функция стационарного гауссовского белого шума соответственно равны:
M{n(t)} = 0; (4.2)
K
2n
(t
1
, t
2
) = M{n(t
1
) n(t
2
)} = N
0
δ(t
2
– t
1
), (4.3)
где N
0
– спектральная плотность белого шума; δ(⋅) – дельта-функция.
Винеровский процесс после линейного преобразования (4.1) остается гауссовским процессом и с учетом (4.2) и (4.3)
имеет при B
0
= 0 соответственно математическое ожидание, дисперсию и корреляционную функцию:
(){} (){}
0
0
=ττ=
∫
dnMtBM
t
t
; (4.4)
()
{}
()(){}
0,
02121
2
00
>=ττττ=
∫∫
ttNddnnMtBM
t
t
t
t
; (4.5)
() (){()
()
.0,0,,min
,
,
,
21210
1220
2110
2121212
2
0
1
0
>>=
=
<
≤
=ττττ=
∫∫
ttttN
tttN
tttN
ddnnMttk
t
t
t
t
B
(4.6)
Очевидно, корреляционную функцию винеровского процесса можно также представить для положительных t
1
и t
2
в ви-
де
()
()
1221
0
212
2
, tttt
N
ttk
B
−−+= . (4.7)
Плотность распределения винеровского процесса имеет вид

()()
()
0,
2
exp
2
1
2
0
>
−
π
= t
D
tB
tN
tBp
. (4.8)
Рассмотрим некоторые свойства приращений винеровского процесса: их некоррелированность на неперекрывающихся
интервалах времени и самоподобие.
Для моментов времени t
2
> t
1
> t
0
> 0 имеем
() () ()
ττ=−
∫
dntBtB
t
t
1
0
01
. (4.9)
Отсюда на основании (4.4) и (4.5) математическое ожидание и версия приращения винеровского процесса соответст-
венно равны:
M{B(t
1
) – B(t
0
)} = 0;
M{(B(t
1
) – B(t
0
))
2
} = N
0
(t
1
– t
0
) ∼ t
1
– t
0
. (4.10)
Взаимная корреляционная функция приращений при выполнении условия (4.9) на основании (4.6) равна
M{[B(t
2
) – B(t
1
)][B(t
1
) – B(t
0
)]} = k(t
1
, t
2
) – k
2
(t
1
, t
1
) – k
2
(t
2
, t
0
) + k
2
(t
1
, t
0
) =
= N
0
t
1
– N
0
t
1
– N
0
t
0
+ N
0
t
0
= 0.
Таким образом, приращения процесса B(t) некоррелированы и, поскольку имеют гауссовское распределение, независи-
мы.
Перейдем к рассмотрению свойств самоподобия. Плотность распределения приращений винеровского процесса при
B(t
0
) ≠ 0 имеет вид
() ( )
[]
()
[]
()
(
)
[]
()
−
−
−−π=−
−
00
2
0
2/1
000
2
exp2
ttN
tBtB
ttNtBtBp
. (4.11)
Изменим масштаб времени в b раз. Ввиду того, что дисперсия процесса также увеличивается в b раз – N
0
b(t – t
0
), для
обеспечения нормировки плотности распределения на единицу необходимо увеличить приращение винеровского процесса в
b
1/2
раз, т.е. изменить масштаб координаты в такое же число раз b
1/2
.
()
[]
() ( )
[]
{}
()
.
2
exp2
)}]()({[
00
2
0
2/1
2/1
00
0
2/1
−
−
−−π=
=−
−
ttbN
btBbtBb
ttbN
btBbtBbp
(4.12)
Очевидно, что плотности (4.11) и (4.12) связаны соотношением b
1/2
p[b
1/2
{B(bt) – B(bt
0
)}] = p[B(t) – B(t
0
)], выражающим
условие самоподобия: плотность вероятности отмасштабированного винеровского процесса, умноженная на коэффициент
b
1/2
, не зависит от выбранного масштаба времени. Как следует из полученного результата, изменение масштаба времени в b
раз сопровождается изменением масштаба приращения координаты винеровского процесса в b
1/2
раз и свойство самоподобия
можно записать также в форме:
b
–1/2
[B(bt) – B(bt
0
)] = B(t) – B(t
0
).
4.2. МОДЕЛИРОВАНИЕ СЕТЕВЫХ ПРОЦЕССОВ
ФРАКТАЛЬНЫМ БРОУНОВСКИМ ДВИЖЕНИЕМ
Приведенные выше модели процессов описывали классическое броуновское движение. Как уже отмечалось ранее, мно-
гие природные явления не укладываются в рамки традиционных моделей, в том числе в модели винеровского процесса. Для
описания этих явлений, обладающих фрактальными свойствами, в работе [23] было введено обобщенное броуновское дви-
жение, которое по определению записывается в форме дробного интеграла
() ()()
ττ−
+Γ
∫
∞−
dBth
Н
tB
е
H
2
1
1
, (4.13)
где dB(τ) – приращение винеровского процесса; Г(⋅) – гамма-функция; Н – введенный в разд. 2 параметр Херста.
Импульсная переходная функция равна
()
()
() ()
<ττ−−τ−
≤τ≤τ−
=τ−
−−
−
.0,
;0,
2/12/1
2/1
HH
H
t
tt
th
(4.14)
Использование в формуле (4.13) импульсной переходной функции степенного вида (4.14) приводит к сильной коррели-
рованной зависимости процесса В
Н
(t) от предшествующих его значений, а также указывает на самоподобный характер фрак-

тального броуновского движения. На основании соотношения h(bt – bτ) = b
H – 1/2
h(t – τ), а также зависимости для винеровско-
го процесса dB(bτ) = b
1/2
dB(τ) из формулы (4.13) получаем B
H
(bt) = b
H
B
H
(t) или
b
–H
B
H
(bt) = B
H
(t), (4.15)
что подтверждает самоподобный характер фрактального броуновского движения. Для приращений этого процесса матема-
тическое ожидание и дисперсия на основании (4.13) с учетом свойств винеровского процесса M{dB(T)} = 0, M{dB(τ
1
)dB(τ
2
)}
= M{n(τ
1
)n(τ
2
)}dτ
1
dτ
2
= N
0
δ(τ
2
– τ
1
)dτ
1
dτ
2
соответственно равны
M{B
H
(t) – B
H
(t
0
)} = 0; (4.16)
M{[B
H
(t) – B
H
(t
0
)]
2
} ∼ (t – t
0
)
2H
. (4.17)
Отметим также, что как для классического, так и для фрактального броуновского движения дисперсии приращений рас-
тут с увеличением разности t – t
0
.
Определим нормированную корреляционную функцию (коэффициент корреляции) стационарных приращений фрак-
тального броуновского движения для двух соседних неперекрывающихся знаковой длительности интервалов времени (t
0
, t
1
)
и (t
1
, t
2
):
()
})]()({[
)]}()([)]()({[
2
01
1201
tBtBM
tBtBtBtBM
tr
HH
HHHH
H
−
−−
=
или при В
H
(t
0
) = 0
)}({
)}({)}2()({
)(
2
2
tBM
tBMtBtBM
tr
H
HHH
H
−
=
. (4.18)
Прибавляя и вычитая в каждом из сомножителей первого слагаемого (4.18) соответственно B(2t) и B(t), после перемно-
жения и приведения подобных членов получаем
.21
)}({
)}2()({
)}({
)}2({
1
)}({
)]}()()2()][2()2()({[
22
2
2
−
−−=
=−
+−+−
=
tBM
tBtBM
tBM
tBM
tBM
tBtBtBtBtBtBM
r
H
HH
H
H
H
HHHHHH
H
(4.19)
Принимая во внимание, что соотношение в квадратных скобках в выражении (4.19) на основании (4.18) равно r
H
(t), а
также учитывая (4.17), имеем окончательно
r
H
(t) = 2
2H–1
– 1. (4.20)
Если (4.20) домножить на M{B
2
H
(t)} ~ t
2H
, то приходим к корреляционной функции приращений на интервалах (0, t) и (t,
2t) фрактального броуновского движения
K
2H
(t) ≈ (2
2H – 1
– 1)t
2H
.
Это выражение указывает на сильную корреляционную зависимость приращений, увеличивающуюся с ростом t.
Заметим, что при Н = 1/2 процесс (4.13) становится винеровским (4.1) с дисперсией и корреляционной функцией при-
ращений, равными ответственно (4.10) и нулю. Используя аналогичный подход, можно от характеристик винеровского про-
цесса перейти к характеристикам фрактального броуновского движения. Например, знание кореляционной функции (4.7)
позволяет записать корреляционную функцию фрактального броуновского движения в форме
K
2H
(t
1
, t
2
) ∼ 1/2[t
1
2H
+ t
2
2H
– |t
1
– t
2
|
2H
]. (4.21)
Коэффициент корреляции для стационарных приращений фрактального броуновского движения на интервалах (t
n
, t
n
– T) и
(t
n + k
, t
n + k
– T) заданной длительности Т разнесения на время kT, где k – параметр смещения, можно представить, как и для
счетных характеристик, выражением
()
Tkr
H
, ∼
() ()
[
]
1
1
1
121
2
1
+α
+α
+α
−+−+ kkk .
При k = 1, что соответствует корреляционной зависимости для приращений процесса на соседних интервалах времени, а
также учитывая соотношение α = 2Н – 1, получаем (4.20). При больших значениях k коэффициент корреляции аппроксими-
руется выражением (3.45)
(
)
Tkr
H
, ∼
() ( )
221
121
2
1
−−α
−=+αα
H
kHHk . (4.22)
Из этого выражения следует, что чем больше параметр Н, тем более протяженной зависимостью обладает r
H
(k, T).
Как и для счетных статистик, можно показать, что поведение спектральной плотности приращений фрактального бро-
уновского движения при ω → 0 описывается зависимостью (3.46).
Если обозначить приращения фрактального броуновского движения на интервалах (t
n
, t
n
– T) через Х
n
, то агрегирован-
ный процесс, сформированный как последовательность средневзвешенных величин из приращений на m одинаковых непе-
рекрывающихся интервалах длительностью Т, описывается соотношением (2.47). У агрегированного процесса приращений,

как и для счетных характеристик, при m → ∞ коэффициент корреляции r
H
(k, T) сохраняет свою структуру и практически не
зависит от параметра m, а дисперсия изменяется согласно соотношению
D
(m)
(T) ∼ m
α – 1
. (4.23)
Напомним, что для короткопротяженных зависимостей дисперсия приращений агрегированного процесса изменяется
как D
(m)
(T) ∼ m
–1
.
Указанная статистика – дисперсия приращений является удобной для фрактальных свойств характеристикой при обра-
ботке экспериментальных данных по дисперсионно-временному графическому методу.
При исследовании на базе фрактального броуновского движения свойств сетевого графика обращаются к рассмотрен-
ной в разд. 3.4 модели ON/OFF режима. В качестве исходных данных используются следующие статистики интервалов. Для
ON интервала ψ
1
(τ) и
() ()
∫
τ
ψ=τ
0
11
duuF – соответственно плотность распределения и функция распределения временных ин-
тервалов; 1 – F
1C
(τ) – функция, описывающая «хвостовое» распределение интервалов;
()
∫
∞
ψ=µ
0
11
duuu – математическое
ожидание интервала. Соответствующие характеристики OFF интервала обозначаются следующим образом: ψ
2
(τ), F
2
(τ), 1 –
F
2C
(τ) и µ
2
. Одним из определяющих поведение сетевого трафика факторов, как уже ранее отмечалось, является «тяжелое»
распределение, а именно, существование значительной по величине вероятности длинных и очень длинных ON/OFF интер-
валов. Последнее ведет к необходимости аппроксимации хвостовой части функции распределения степенной зависимостью
F
1C
(τ) ∼ L
1
(τ)τ
–α
1
, F
2C
(τ) ∼ L
2
(τ)τ
–α
2
,
где L
1
(τ) > 0 и L
2
(τ) > 0 – постоянные величины или медленно изменяющиеся во времени ограниченные функции; α
1
и α
2
–
дробные фрактальные параметры.
Будем считать, что источник генерирует бинарную последовательность пакетов: R(t) = 1 означает, что в момент време-
ни t есть серия пакетов, a R(t) = 0 – пакеты отсутствуют. Длины интервалов независимы и в общем случае неодинаково рас-
пределены. При реализации режима ON/OFF рассматриваются m независимых источников, каждый из которых посылает
свою последовательность пакетов R
(i)
(t). В результате суперпозиции всех источников получаем последовательность
()
()
∑
=
m
i
i
tR
1
. С учетом изменения масштаба времени в b раз агрегированное число пакетов на интервале (0, bt) равно
()
()
()
()
∫
∑
τ
τ=
=
bt
m
i
im
dRbtW
0
1
. (4.24)
В [24] доказывается теорема, что при b → ∞ и m → ∞ центрированная составляющая агрегированного случайного процес-
са ON интервалов сходится по вероятности к фрактальному броуновскому движению
()
() ()
tBambtbtWb
H
mH
m
b
1
21
1
lim =
µ+µ
µ
−
−
∞→
∞→
, (4.25)
где нормирующий параметр
lim11
σ= mLa , σ
lim
= f
(α
1
, α
2
, µ
1
, µ
2
, L
1
, L
2
).
Сравнивая (4.25) с выражением для фрактального броуновского движения (3.15), можно убедиться в общности подхо-
дов при анализе рассматриваемых процессов, что позволяет охарактеризовать поведение сетевого трафика через обладаю-
щие свойствами самоподобия статистики фрактального броуновского движения.
Например, можно показать, что процесс
()
()
()
ττ=
∫
dRtW
t
0
1
(
)
1
=
=
bm имеет дисперсию при достаточно больших t.
D
W
(t) = M{W
2
(t) – [M{W(t)}]
2
} ∼ L(t)σ
2
lim
t
2H
.
К числу процессов, аппроксимируемых фрактальным броуновским движением, следует отнести RTT (round trip time) –
задержку [25]. Указанная задержка является важной характеристикой, обеспечивающей нормальное функционирование TCP-
соединения в фазе медленного старта и поэтому требующей тщательную настройку и контроль. RTT-задержка измеряется на
стороне источника временным интервалом между моментами посылки пакета в направлении приемника и получения пакета
подтверждения. Эта задержка складывается из времени обработки и распространения, а также затрат времени на очереди
вдоль маршрута прохождения пакета. Появление очередей является следствием конечного значения скорости обработки ин-
формации в сетевых устройствах, например, из-за ограниченного объема памяти находящихся в промежуточных узлах сети
буферов маршрутизаторов, задержек в обработке пакетов на стороне приемника и источника. Ранее это обстоятельство слу-
жило основанием для объяснения протяженной зависимости и самоподобия сетевого трафика. Очевидно, одновременное
сосуществование в режиме реального времени этих процессов предполагает взаимосвязь между ними и неизбежно приводит
к выводу об общей природе источника фрактальных свойств сетевого трафика и RTT-задержки.
Для стационарного процесса RTT-задержку, которую обозначим через T
i
, можно записать в виде (рис. 4.1)
Т
i
= T
1i
+ T
2i
+ T
пp
,
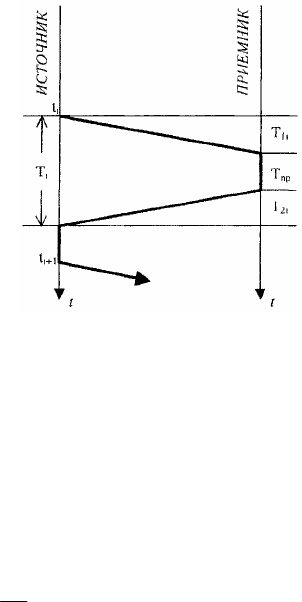
где i = 1, 2, ... – номера задержек (циклов); интервалы T
1i
и Т
2i
соответствуют временам пересылки пакета от источника к
приемнику и обратно; Т
пp
– время обработки информации в приемнике.
Рис. 4.1. Процесс RTT-задержки
Совокупность интервалов Т
i
образует дискретную последовательность RTT-задержек. Интервалы Т
1i
и T
2i
своим сущест-
вованием обязаны задержкам в обработке и передаче информации, а также наличию очередей в промежуточных узлах сети. Для
известного маршрута движения пакета можно выделить постоянную минимальную обусловленную отсутствием очередей со-
ставляющую T
0
и случайную составляющую из-за задержек в очередях и связанную со случайным поведением сетевого трафи-
ка ∆T
i
: T
i
= T
0
+ ∆T
i
. Рассматривая выражение T
i
– M{T
i
}, где M{T
i
} = T
0
+ ∆T
ср
; ∆T
ср
– среднее значение приращения RTT-
задсржки, в качестве случайного приращения броуновского движения, сформируем для момента времени t
n
фрактальный бро-
уновский процесс
()
()
[]
∑
=
∆+−=
n
i
inH
TTTtB
1
ср0
. (4.26)
Полагаем, что моменты времени t
i
(i = n,1 ) образуют регулярную последовательнотсь дискретных временных отсчетов.
Для определенности интервалы между отсчетами принимаем равными средней величине RTT-задсржки ∆ = Т
0
+ ∆Т
ср
. В со-
отношении (4.21) отождествим текущие времена t
2
и t
1
с моментами времени t
n + k
и t
n
(t
n + k
– t
n
= k∆), где k – параметр смеще-
ния. Используя выражение (4.26), запишем соотношение для корреляционной функции процесса В
H
(t)
k
2H
(t
1
, t
2
) = k
2H
(t
n
, t
n + k
) =
= M{B(t
n
)B(t
n + k
)} ∼ 1/2[
H
n
t
2
+
H
kn
t
2
+
– |t
n + k
– t
n
|
2H
]. (4.27)
Коэффициент корреляции для стационарных приращений процесса (4.26) на заданном интервале длительностью Т при
достаточно больших значениях k и Т аппроксимируется известным выражением (4.22).

5. ПРОГНОЗИРОВАНИЕ И УПРАВЛЕНИЕ
ПРОПУСКНОЙ СПОСОБНОСТЬЮ
В КОМПЬЮТЕРНЫХ СЕТЯХ
5.1. ПРОГНОЗИРОВАНИЕ ПРОПУСКНОЙ СПОСОБНОСТИ
В СЕТЯХ
Актуальность постановки задачи прогнозирования и ее решения заключается в том, что данные прогноза о пропускной
способности позволяют получить дополнительные сведения для решения задачи управления, а именно формирования алго-
ритма предотвращения перегрузки. Решение указанной задачи, как правило, сводится к определению алгоритма с адаптив-
ным механизмом перенастройки отдельных сетевых компонент. В качестве одного из вариантов использования этого меха-
низма можно указать на алгоритм изменения текущего окна TCP-соединения для предотвращения перегрузки и уменьшения
тем самым потерь в пропускной способности сети. Если процесс передачи информации не столь критичен к потере пакетов,
в качестве еще одного примера применения этого алгоритма можно привести управление потоками данных протоколом UDP
через механизм изменения интенсивности числа посланных пакетов на отдельных участках сети.
При прогнозе оценка процесса формируется не на конечном отрезке наблюдения, а вне его на некотором временном ин-
тервале упреждения. Предварительно получим результаты для непрерывного времени, а затем обобщим их на процессы в
дискретном времени. Выразим коэффициент корреляции через корреляционную функцию k
2
(t
1
, t
2
) и дисперсию D
t
1
случай-
ного процесса следующим образом:
()
()
1
212
21
,
,
t
D
ttk
ttr =
, (5.1)
где
() ( )
∫∫
∞
∞−
∞
∞−
==
1
,,;,,
212211
0
2
0
1212 t
Ddxdxtxtxpxxttk
()
() () ()
∫
∞
∞−
µ−==
2121
0
2111
2
0
1
,, xxdxtxpx
и
()
21
µ
– соответственно центрированная составляющая и математическое ожидание случайного процесса для t
1(2)
моментов вре-
мени; p(x
1
, t
1
; x
2
, t
2
) и p(x
1
, t
1
) – двумерная и одномерная плотности вероятностей.
Используя формулу для условных плотностей вероятности, представим корреляционную функцию в виде
() () ( )
∫∫
∞
∞−
∞
∞−
=
121122
0
211
0
1212
,|,,, dxdxtxtxpxtxpxttk ,
где p(x
2
, t
2
| x
1
, t
1
) – условная плотность вероятности.
Полагаем сигнал х
1
известным, и поэтому соответствующая ему плотность вероятности принимает дельтаобразный вид
p(x
1
, t
1
) = δ(x – x
1
).
Используя фильтрующие свойства дельта-функции, приходим к следующим выражениям статистик:
() ( )
21122
0
2
0
1212
,|,, dxtxtxpxxttk
∫
∞
∞−
= ; (5.2)
2
0
1
1
xD
t
= . (5.3)
Обозначим оценку прогноза процесса в момент времени t
2
через
0
2
x
)
.
Дисперсия ошибки прогноза при квадратической функции потерь имеет вид
()
()
∫
∞
∞−
−
212
2
0
2
0
2
| dxxxpxx
)
. (5.4)
После дифференцирования соотношения (5.4) по
0
2
x
)
, приравнивания результата дифференцирования нулю получаем
оценку, соответствующую минимуму среднеквадратической погрешности (оптимальную в среднеквадратическом смысле)
{}
()
21122
0
21
0
2
0
2
,|,| dxtxtxpxxxMx
∫
∞
∞−
==
)
. (5.5)
После подстановки соотношения (5.5) в (5.2), а затем в формулу (5.1), с учетом (5.3) получим выражение оценки про-
гноза на интервале упреждения t
2
– t
1
, по известному значению
0
1
x в момент времени t
1
(
)
0
112
0
2
, xttrx =
)
. (5.6)

На основании полученных результатов решим задачи прогноза для счетных характеристик сетевого трафика и фрак-
тального броуновского движения. Для первого случая оптимальный прогноз означает нахождение оптимальной в средне-
квадратическом смысле оценки числа отсчетов Х
n + k
в интервале (t
n + k
, t
n + k
– T), отстоящем от последнего результата наблю-
дения – числа отсчетов Х
n
в интервале (t
n
, t
n
– T) на время kT, где k – параметр смещения. Полагая процесс стационарным,
принимаем интенсивность точечного процесса работы равной известной постоянной величине
λ. Для счетных характеристик
интервал упреждения и коэффициент корреляции становятся равными соответственно kT и r (k, T). Отождествляя t
2
и t
1
с
моментами времени (k + n) и nТ, а также полагая
µ
1
= µ
2
= λT, получаем из выражения (5.6) оптимальную оценку прогноза
отсчета
kn
X
+
)
по известному отсчету X
n
:
(
)
(
)
TTXTkrX
nkn
λ+λ−=
+
,
)
. (5.7)
Значение r
(k, T) в зависимости от исходных данных и особенностей решения задачи принимает одну из форм (3.43),
(3.44) и (3.45). Качество прогноза для рассматриваемой задачи оценим по величине дисперсии ошибки при заданном пара-
метре смещения k:
}){(
22
knknk
XXM
++
−=ε
)
.
После возведения выражения в круглых скобках в квадрат, определения математического ожидания, а также принимая
во внимание (5.7), имеем
()( )
(
)
{
}
(
)
(
)
(
)
DTkCTkrDTkrXTTXTkrM
knnk
+−=−λ+λ−=ε
+
,,2,,
2
2
2
.
(5.8)
При выводе этого соотношения было учтено, что
()
,,}{
;}{}{
22
2222
TTkCXXM
TDXMXM
knn
knn
λ+=
λ+==
+
+
где C(k, T) – введенная ранее корреляционная функция числа счетов в разнесенных на время kT интервалах длительностью Т
(3.22);
C(0, T) = D. Умножив и поделив второе слагаемое (5.8) на D и учитывая, что r (k, T) = C(k, T) / D, получаем окончательно
()
],1[
22
TkrD
k
−=ε . Как следует из этого выражения, с возрастанием параметра k, что соответствует увеличению глубины
прогноза, качество прогноза ухудшается (увеличивается ошибка), так как коэффициент корреляции уменьшается. Обратим
внимание на то, что в связи с протяженной зависимостью статистики r (k, T) обеспечивается для выбранного параметра k
лучшее качество прогноза по сравнению с короткопротяженными статистиками обычных моделей случайных процессов. В
пределе при k
→ ∞ дисперсия ошибки прогноза стремится к априорной дисперсии C(0, T) = D. Прогноз можно улучшить,
если использовать, помимо последнего, ряд предшествующих возможно с разными весовыми коэффициентами измерений
общим числом m. В прогнозе для этого случая, кроме того, можно учесть тенденцию изменений числа отсчетов (прираще-
ний) точечного процесса. В простом варианте агрегирования получаем для оптимальной оценки прогноза выражение сле-
дующего вида
()
()
[]
nmTTXTjnkr
m
X
n
mnj
jkn
≤≤λ+λ−−+=
∑
+−=
+
1,,
1
1
)
. (5.9)
На основании свойств фрактального броуновского движения получим прогнозируемую оценку ON интервалов (дли-
тельностей пачек пакетов) к моменту времени t
2
по известным значениям характеристик в момент времени t
1
, t
2
> t
1
> 0. В
качестве исходной для получения прогноза рассматривается формула (5.6). Для фрактального броуновского движения коэф-
фициент корреляции (5.1) с учетом формулы (4.21) имеет вид
()
()
()
[
]
,11
2
1
2
1,
,
2
2,1
2
2,1
2
1
2
12
2
2
2
1
1
212
21
−−+=
=
−−+
==
H
H
H
H
HH
H
H
H
SS
t
tttt
tD
ttk
ttr
(5.10)
где S
1, 2
= t
2
/
t
1
.
Оптимальный в среднеквадратическом смысле прогноз фрактального броуновского движения
()
2
tB
H
)
по известному
значению В
H
(t
1
) (последнему, измеренному в момент t
1
) описывается следующим соотношением
() () (){} ()
1
2
2,1
2
2,1122
11
2
1
|
tBSStBtBMtB
H
H
H
HHH
−−+==
)
. (5.11)
Перейдем к прогнозу агрегированного процесса (4.24). Используя формулу (5.11), а также выражение (4.25), можно по-
казать, что при b = 1 и достаточно большом m оптимальная в среднеквадратическом смысле оценка прогноза в момент вре-
мени
()
()
22
tWt
m
)
− близка по вероятности процессу
()
()
2
21
1
1
21
1
1
2
2,1
2
2,1
11
2
1
t
m
t
m
tWSS
m
H
H
µ+µ
µ
+
µ+µ
µ
−
−−+
,
где W
m
(t
1
) – известное к моменту времени t
1
значение агрегированного потока пакетов.
При определении прогнозируемой оценки RТТ-задержки воспользуемся соотношением (5.6) фрактального броуновско-
го движения. Для этого процесса на основании соотношений (4.27) и (5.11) коэффициент корреляции и оптимальная в сред-
неквадратическом смысле оценка прогноза в момент времени t
n + k
и известном значении процесса в момент t
n
соответственно
равны:
()
−−+=
−−+
=+
++
++
H
knn
H
knn
H
n
H
nkn
H
kn
H
n
H
SS
t
tttt
knnr
2
,
2
,
2
2
22
11
2
1
2
,
;
(
)
(
)()
{
}( )
(
)
nHHnHknHknH
tBknnrtBtBMtB +==
++
,|
)
, (5.12)
где S
n, n + k
= t
n + k
/
t
n
.
Как уже ранее отмечалось, качество прогноза можно улучшить, и для оценки прогноза использовать не только послед-
нее, но и ряд предшествующих измерений. Обозначим общее число таких измерений через m . В этом случае после агреги-
рования оптимальная оценка прогноза фрактального броуновского движения становится равной
()
()
∑
+−=
+++
−−+=
n
mnj
jH
H
knj
H
knjknH
tBSS
m
tB
1
2
,
2
,
11
2
1
)
, (5.13)
где S
j, n + k
= t
n + k
/
t
j
.
Оптимальная оценка прогноза RTT-задсржки для момента времени t
n + k
принимает вид
(
)()
ср01
TTtBtBT
knHknHkn
∆++−=
−+++
)
)
)
. (5.14)
Остановимся подробней на оценке прогноза следующего за последним измеренным для момента времени t
n
значением
остального броуновского движения. На основании формулы (5.14) она равна
(
)()
ср011
TTtBtBT
nnHn
∆++−=
++
)
)
. (5.15)
В случае использования ряда предшествующих измерений общим числом m для оценки прогноза сохраняется
cooтношение (5.15), где
()
()
∑
=
+++
−−+=
n
j
jH
H
nj
H
njnH
tBSS
m
tB
1
2
1,
2
1,1
11
2
1
)
.
Такую же по величине оценку прогноза можно получить через коэффициент корреляции соседних приращений фрак-
тального броуновского движения. Рассматривая случайное изменение RTT-задержки как приращение фрактального бро-
уновского движения B
H
(t
n + 1
) – B
H
(t
n
), коэффициент корреляции приращений можно представитъ в виде:
()
{}
,
})]()({[
)]()([)]()([
)(0}{
)(}{
,1
2
1
11
2
ср0
2
2
ср01
−
+−
+
−
−−
=
=
∆
∆+−
=∆
nHnH
nHnHnHnH
n
nn
H
tBtBM
tBtBtBtBM
TTTM
TTTTM
r
где ∆ = Т
0
+ ∆Т
ср
.
Для стационарного процесса приращений статистики инвариантны к начальному временному отсчету. Поэтому на ос-
новании формулы (4.18) при В
H
(t
n – 1
) и n = 1 можно записать
()
)}({
)}({)]}()({[
,1
1
2
1
2
21
tBM
tBMtBtBM
r
HHH
H
−
=∆
,
где t
2
– t
1
= t
1
= ∆.
После вычислений по уже известной методике разд. 4 получаем
r
H
(1, ∆) = 2
2H – l
– 1.
Оценка прогноза RTT-задержки принимает вид
ср0ср01
)]()[,1( TTTTTrT
nHn
∆++∆+−∆=
+
)
.
Можно показать, что как и для счетных характеристик, в рассматриваемом случае величина ошибки прогноза зависит
от характера поведения коэффициента корреляции. Чем сильнее статистическая зависимость между соседними отсчетами
процесса, чему не в малой степени способствует протяженная зависимость, тем медленнее спадает коэффициент корреляции
и тем самым оказывается меньше величина ошибки прогноза.
