Громкович Ю. Теоретическая информатика. Введение в теорию автоматов, теорию вычислимости, теорию сложности, теорию алгоритмов, рандомизацию, теорию связи и криптографию
Подождите немного. Документ загружается.


n = p
m
(n/p
m
)
Bin (dlog
2
me)·Bin(m)·Bin(n/p
m
)
Prim (k)
n = p
m
· (n/p
m
)
Bin (dlog
2
dlog
2
dlog
2
(m + 1)eee)Bin(dlog
2
dlog
2
(m + 1)ee)
Bin(dlog
2
(m + 1)e)Bin(m)Bin(n/p
m
) ?
∗
Prim (k)
∗
p
1
, p
2
, p
3
, . . .
c m
K (p
m
) ≤ dlog
2
p
m
e − dlog
2
log
2
p
m
e + c.
L
Σ
bool
= {0, 1} x
x
x
x {0, 1}
{0, 1}


•

•
•
•
Σ = {a
1
, a
2
, . . . , a
k
}
input = a
1
i
1
input = a
2
i
2
input = a
k
i
k
a
1
, a
2
, . . . , a
k
a
j
i
j
i
j
i
j
0, 1, 2 , 3, . . .
0 Σ 0 1
input = 1 i j
1
2

m {0, 1, 2, . . . , m − 1}
F ⊂ {0, 1, 2, . . . , m − 1}
F
j ∈ F
j ∈ {0, 1, 2, . . . , m − 1} − F
L
(Σ, L) L
A Σ
bool
input = 1 1 2
input = 1 0 3
input = 0 0 3
input = 0 1 2
F = {0, 3} A
1011 0
1 1
0 1 3 3 1
2 1
3 3 ∈ F
1011
0000 111
. . .

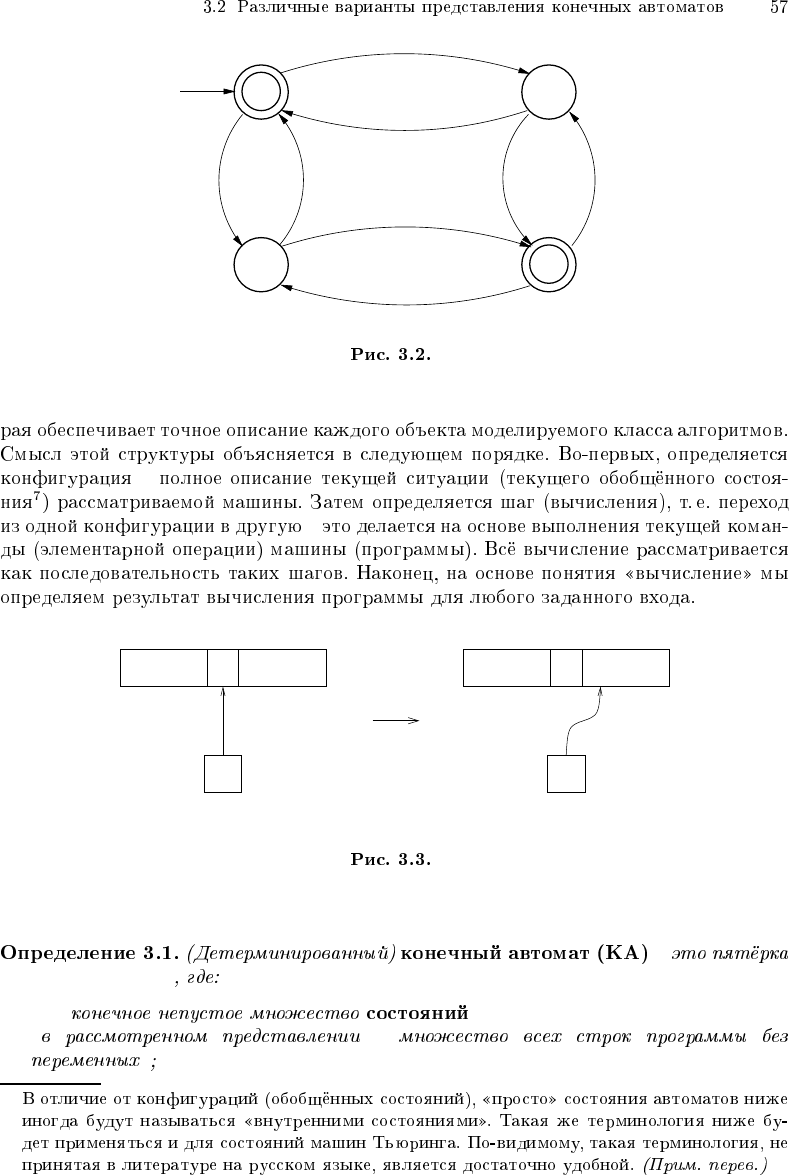
A
G(A)
A G(A)
A
A i j
b G(A) (i, j) b
a ∈ Σ G(A)
|Σ|
G(A) A
0 3 F
0
3
4
5
6
G
|{(v , u) | (v, u) }|
0000
0
1
1
1
1
1
2 3
q p
(a) (b)
aa
M = (Q, Σ, δ, q
0
, F )
• Q
{
}
7

• Σ M
{ Σ }
• q
0
∈ Q
{ 0 }
• F ⊆ Q
• δ Q × Σ Q
M
{δ(q, a) = p a M
q p }
M Q × Σ
∗
{ M (p, w) ∈ Q × Σ
∗
M
p w
w
}
(q
0
, x) ∈ {q
0
}×Σ
∗
M x
{ (q
0
, x)
M x.}
Q × {λ}
M
|−−
M
⊆ (Q × Σ
∗
) × (Q × Σ
∗
),
(q, w)
|−−
M
(p, x) ⇔ w = ax, a ∈ Σ δ(q, a) = p .
{
M q
a }
C M
C = C
0
, C
1
, . . . , C
n
i 0 ≤ i ≤ n − 1
C
i
|−−
M
C
i+1
{
M
C
0
|−−
M
C
1
|−−
M
. . .
|−−
M
C
n
C
0
, C
1
, . . . , C
n
}
C M x ∈ Σ
∗
C
0
= (q
0
, x)
C
n
∈ Q × {λ}.
8

{ x (q
0
, x)
M x
}
C
n
∈ F × {λ} C
M x M
x
C
n
∈ (Q − F ) × {λ} C
M x M x
{ M x ∈ Σ
∗
}
L(M) M
L(M) = {w ∈ Σ
∗
| M w
(q, λ) q ∈ F }
= {w ∈ Σ
∗
| M
w}.
L(KA) = {L(M) | M }
L L(KA)
A
M = (Q, Σ, δ, q
0
, F )
• Q = {q
0
, q
1
, q
2
, q
3
}
• Σ = {0, 1}
• F = {q
0
, q
3
}
• δ(q
0
, 0) = q
2
δ(q
0
, 1) = q
1
δ(q
1
, 0) = q
3
δ(q
1
, 1) = q
0
• δ(q
2
, 0) = q
0
δ(q
2
, 1) = q
3
δ(q
3
, 0) = q
1
δ(q
3
, 1) = q
2
δ
q
0
q
2
q
1
q
1
q
3
q
0
q
2
q
0
q
3
q
3
q
1
q
2
A
G(A)
9
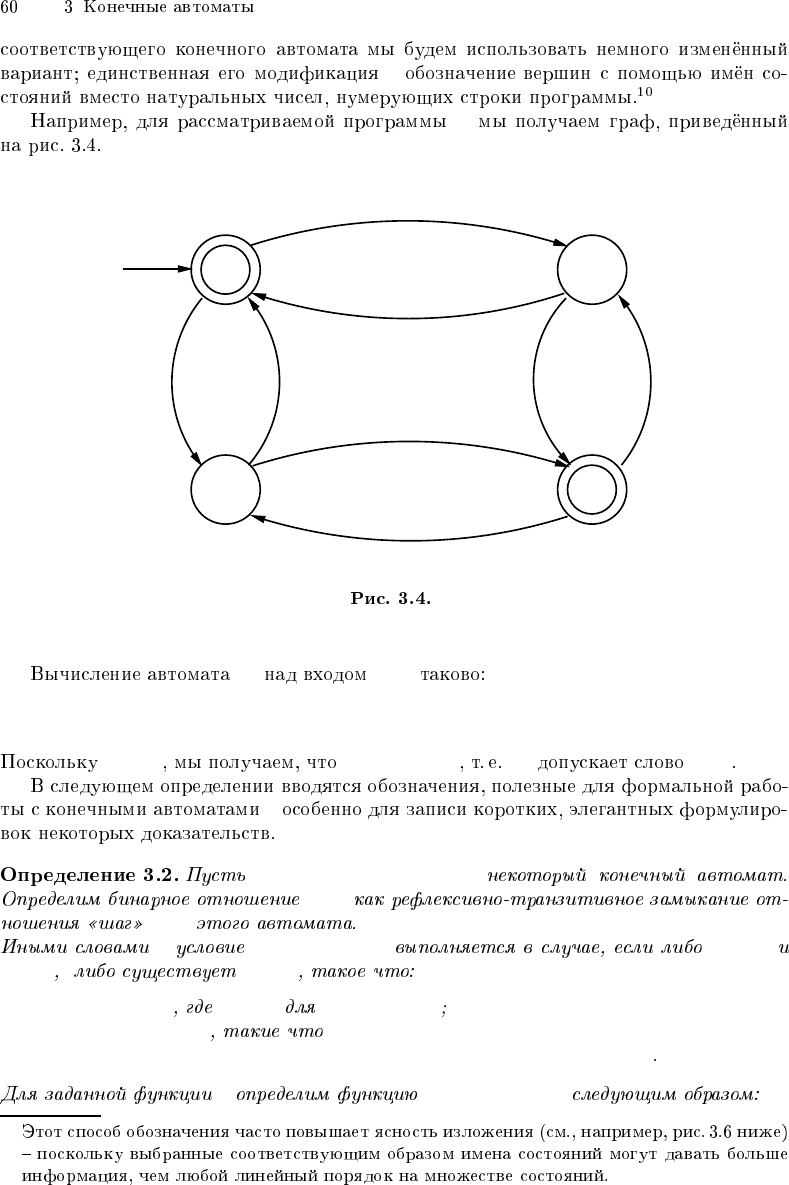
A
q
0
q
1
q
2
q
3
0000
1
1
1
1
M 1011
(q
0
, 1011)
|−−
M
(q
1
, 011)
|−−
M
(q
3
, 11)
|−−
M
(q
2
, 1)
|−−
M
(q
3
, λ).
q
3
∈ F 1011 ∈ L(M) M 10 11
M = (Q, Σ, δ, q
0
, F )
∗
|−−
M
|−−
M
(q, w)
∗
|−−
M
(p, u) q = p
w = u k ∈ IN
• w = a
1
a
2
. . . a
k
u a
i
∈ Σ i = 1, 2, . . . , k
• ∃r
1
, r
2
, . . . , r
k−1
∈ Q
(q, w)
|−−
M
(r
1
, a
2
. . . a
k
u)
|−−
M
(r
2
, a
3
. . . a
k
u)
|−−
M
···(r
k−1
, a
k
u)
|−−
M
(p, u)
δ
ˆ
δ : Q × Σ
∗
→ Q
10
