Громкович Ю. Теоретическая информатика. Введение в теорию автоматов, теорию вычислимости, теорию сложности, теорию алгоритмов, рандомизацию, теорию связи и криптографию
Подождите немного. Документ загружается.


B
i,t
1
t i
|Γ | = m B
i,t
O(1)
B =
^
0≤i,t≤p(|w|)
B
i,t
B O ((p(|w|))
2
)
t
C
t
= U(Sh0, ti, Sh1, ti, . . . , Shs, ti).
Sh0, ti, . . . , Shs, ti
C
t
M t
|Q| = s + 1
C
t
O(1)
C
C =
^
0≤t≤p(|w|)
C
t
.
C M
C O(p(|w|))
D
i,j,t
= (Chi, j, ti ↔ Chi, j, t + 1i) ∨ Hhi, ti
1 ≤ j ≤ m 0 ≤ t ≤ p(|w|)−1 (t+1)
Hhi, ti = 0 i
D
i,j,t
O(1)
D
D =
^
0≤i≤p(|w|)
1≤j≤m
0≤t≤p(|w|)−1
D
i,j,t
.
D O ((p(|w|))
2
)
i t j ∈ {1, . . . , m} k ∈ {0, 1, . . . , s}
E
i,j,k,t
Chi, j, ti ∨ Hhi, ti ∨ Shk, ti∨
W
l
(Chi, j
l
, t + 1i ∧ Shk
l
, t + 1i ∧ Hhi
l
, t + 1i)
28
x ↔ y (x ∨ y) ∧(x ∨ y)
D
i,j,t
↔ (Chi, j, ti ∨ Chi, j, t + 1i ∨ Hhi, t i) ∧ (Chi, j, ti ∨ Chi, j, t + 1i∨ Hhi, ti ) .
29
m

l M (q
k
, X
j
)
(q
k
l
, X
j
l
, z
l
) ∈ δ(q
k
, X
j
), z
l
∈ {L, R, N },
i
l
= i + ϕ(z
l
), ϕ(L) = −1, ϕ(R) = 1, ϕ(N) = 0.
E
i,j,k,t
Chi, j, ti i t X
j
Hhi, ti t i
Shk, ti M t q
k
t
(q
k
, X
j
) i
E
i,j,k,t
(q
k
, X
j
)
(t+1) i
δ
(q
k
, X
j
) l (q
k
l
, X
j
l
, z
l
)
(q
k
, X
j
) i X
j
X
j
l
M q
k
l
z
l
l E
i,j,k,t
O(1)
E =
^
0≤i,t≤p(|w|)
1≤j≤m
0≤k≤s
E
i,j,k,t
,
O((p(|w|))
2
)
M w
¢w 0
q
0
w = X
j
1
X
j
2
. . . X
j
n
j
r
∈ {1, 2, . . . , m} n ∈ IN
0
X
1
= ¢ M
t = 0
F = Sh0, 0i ∧ Hh0, 0i∧ Ch0, 1, 0i
∧
^
1≤r≤n
Chr, j
r
, 0i ∧
^
n+1≤d≤p(|w|)
Chd, m, 0i.
F O (p(|w|)) F
G
G = Shs, p(|w|)i;
p(|w|)
q
accept
B
M
(w)

• B
M
(w)
M w B
M
(w)
M
w
• B
M
(w) M w
p(|w|)
B
M
(w) O((p(|w|))
3
)
Σ
logic
O((p(|w|))
2
)
O(log
2
(|w|)) B
M
(w)
B
M
O((p(|w|))
3
· log
2
(|w|)).
B
M
L(M) SAT ut
NP SAT
NP
NP
NP SAT
P NP
L
1
L
2
L
1
≤
p
L
2
L
1
NP
L
2
NP
NP
NP
NP
SAT = {Φ | Φ };
3 SAT = {Φ | Φ 3 };
CLIQUE = {(G, k) | G
k };
VC = {(G, k) | G
k},
30
SAT
L
diag

• 3
• G = (V, E) U ⊆ V
E
U
Φ ϕ
Φ
ϕ ϕ(Φ)
SAT ≤
p
CLIQUE.
Φ = F
1
∧F
2
∧ . . . ∧ F
m
F
i
= (l
i1
∨ l
i2
∨··· ∨ l
ik
i
), k
i
∈ IN
i = 1, 2, . . . , m .
(G, k)
Φ ∈ SAT ⇔ (G, k) ∈ CLIQUE.
k = m
G = (V, E)
V = {[i, j] | 1 ≤ i ≤ m, 1 ≤ j ≤ k
i
}
Φ
E = {{[i, j], [r, s]} | [i, j], [r, s] ∈ V, i 6= r l
ij
6= l
rs
} {u, v}
u
v
Φ = (x
1
∨ x
2
) ∧ (x
1
∨x
2
∨x
3
) ∧ (x
1
∨ x
3
) ∧ x
2
.
k = 4 G
(G, k) Φ
Φ ⇐⇒ G k = m.
G l
ij
l
rs
i 6= r
1 G
Φ
1
31
32
ϕ ϕ(l
ij
) = ϕ(l
r s
) = 1
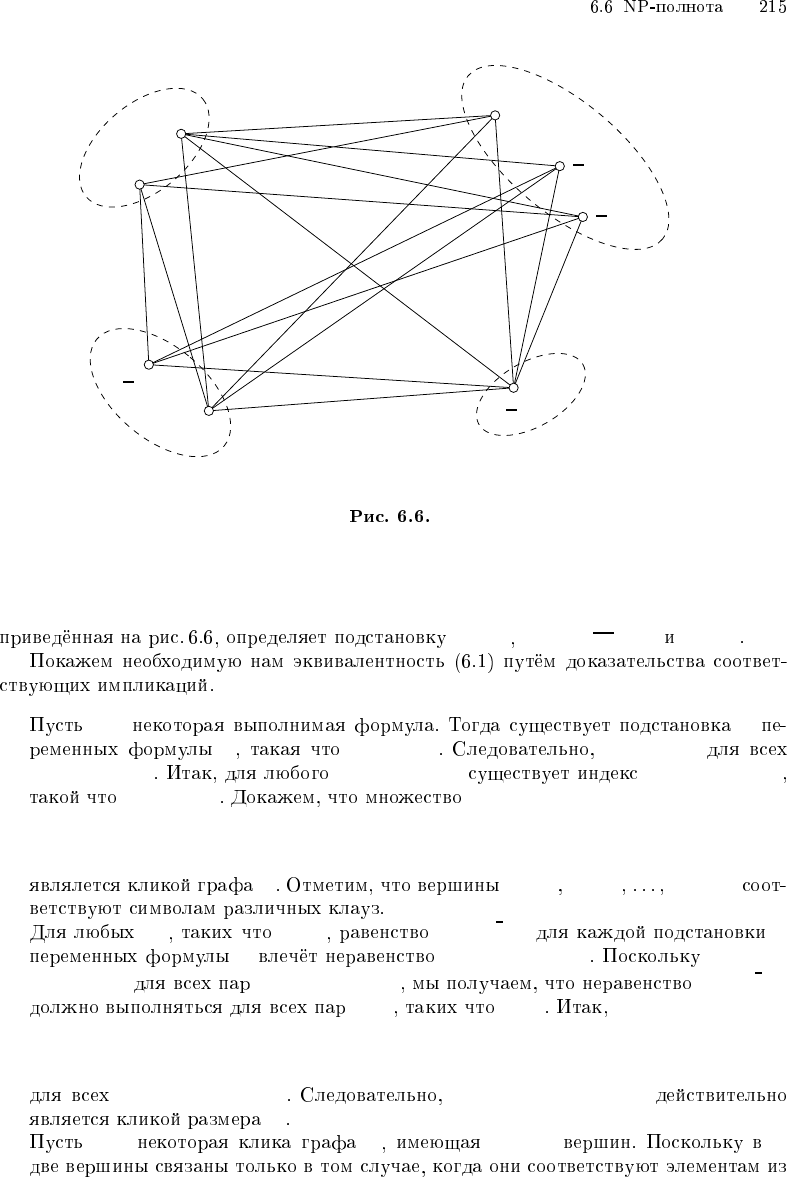
x
1
x
1
x
2
x
3
x
1
x
2
x
2
x
3
[1, 1]
[1, 2]
[2, 1]
[2, 2]
[2, 3]
[3, 1]
[3, 2]
[4, 1]
F
1
F
2
F
3
F
4
{[1, 1], [2, 1], [3, 2], [4, 1]},
x
1
= 1 x
2
= 0 (x
2
= 1) x
3
= 1
⇒ Φ ϕ
Φ ϕ(Φ) = 1 ϕ(F
i
) = 1
i ∈ {1, . . . , m} i ∈ {1, . . . , m} α
i
∈ {1 , . . . , k
i
}
ϕ(l
iα
i
) = 1
{[i, α
i
] | 1 ≤ i ≤ m}
G [1, α
1
] [2, α
2
] [m, α
m
]
i, j i 6= j l
iα
i
=
l
jα
j
ω
Φ ω(l
iα
i
) 6= ω(l
jα
j
)
ϕ(l
iα
i
) =
ϕ(l
jα
j
) = 1
i, j ∈ {1, . . . m} l
iα
i
6=
l
jα
j
(i, j) i 6= j
{[i, α
i
], [j, α
j
]} ∈ E
i, j ∈ {1, . . . , m} {[i, α
i
] | 1 ≤ i ≤ m}
m
⇐ Q G k = m G
α
1
, α
2
, . . . , α
m
, α
p
∈ {1, 2, . . . , k
p
} p = 1, . . . , m
Q = {[1, α
1
], [2, α
2
], . . . , [m, α
m
]}.
G
ϕ Φ
ϕ(l
1α
1
) = ϕ(l
2α
2
) = ··· = ϕ(l
mα
m
) = 1.
ϕ(F
1
) = ϕ(F
2
) = ··· = ϕ(F
m
) = 1,
ϕ Φ
ut
CLIQUE ≤
p
VC.
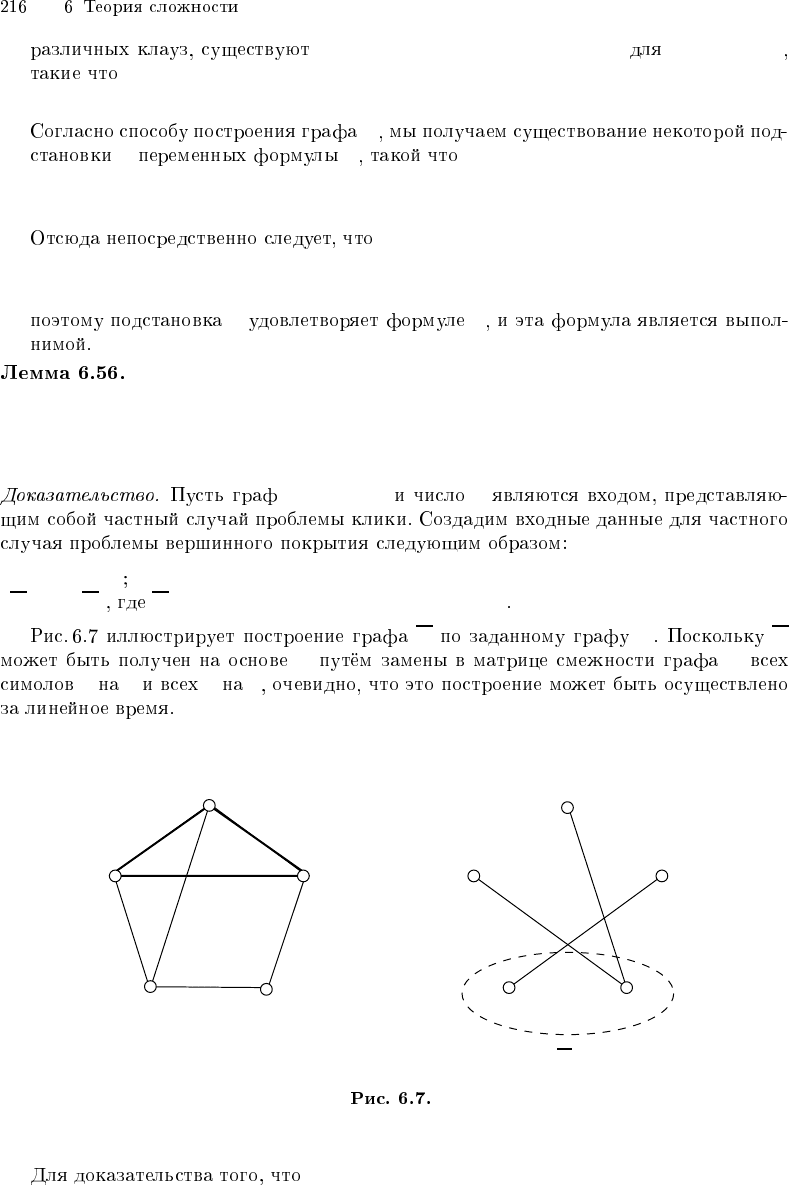
G = (V, E) k
m := |V | − k
G = (V, E) E = {{v, u} | u, v ∈ V, v 6= u, {u, v} /∈ E}
G G G
G G
1 0 0 1
v
1
v
1
v
2
v
2
v
3
v
3
v
4
v
4
v
5
v
5
G
G

(G, k) ∈ CLIQUE ⇐⇒ (G, |V | − k) ∈ VC
S ⊆ V G ⇔ V − S G
{v
1
, v
2
, v
5
} G {v
3
, v
4
} G
{v
1
, v
4
, v
6
} {v
2
, v
3
} {v
2
, v
3
}
{v
1
, v
4
, v
5
}
⇒ S G G
S
G V −S
V −S G
⇐ C ⊆ V G
G
C E {u, v}
u, v ∈ V −C {u, v} ∈ E u, v ∈ V −C u 6= v
V − C G ut
3
3 3 SAT
3
ϕ X =
{x
1
, . . . , x
n
} ϕ : X → {0, 1} Y = {y
1
, . . . , y
r
}
X ∩ Y = ∅
ω : X ∪ Y → {0, 1} ϕ : X → {0, 1}
X ∪ Y
ω(z) = ϕ(z) z ∈ X.
SAT ≤
p
3 SAT.
F = F
1
∧ F
2
∧ . . . ∧ F
m
{x
1
, . . . , x
n
} C
F F ∈ SAT C
C ∈ 3 SAT F C
F
1
, . . . , F
m
F
i
C
i
= F
i
F
i
= z
1
∨ z
2
∨ ··· ∨ z
k
, k ≥ 4, z
i
∈ {x
1
, x
1
, ···, x
n
, x
n
}.
C
i

{x
1
, . . . , x
n
, y
i,1
, y
i,2
, . . . , y
i,k−3
},
y
i,1
y
i,2
y
i,k−3
C
j
j 6= i
C
i
= (z
1
∨ z
2
∨y
i,1
) ∧ (y
i,1
∨ z
3
∨ y
i,2
) ∧ (y
i,2
∨ z
4
∨ y
i,3
)
∧···∧ (
y
i,k−4
∨z
k−2
∨ y
i,k−3
) ∧ (y
i,k−3
∨ z
k−1
∨ z
k
).
F
i
= x
1
∨ x
3
∨ x
2
∨ x
7
∨ x
9
C
i
= (x
1
∨x
3
∨y
i,1
) ∧ (y
i,1
∨ x
2
∨ y
i,2
) ∧ (y
i,2
∨ x
7
∨ x
9
).
F = F
1
∧ ··· ∧ F
m
C = C
1
∧ ··· ∧ C
m
ϕ {x
1
, . . . , x
n
} F
i
ϕ
0
ϕ
{x
1
, . . . , x
n
, y
i,1
, . . . y
i,k−3
} C
i
⇒ ϕ {x
1
, x
2
, . . . , x
n
} ϕ(F
i
) = 1
j ∈ {1, . . . , k} ϕ(z
j
) = 1
ϕ
0
: {x
1
, . . . , x
n
, y
i,1
, . . . , y
i,k−3
} → {0, 1},
ϕ(x
l
) = ϕ
0
(x
l
) l = 1, . . . , n
ϕ
0
(y
i,1
) = ··· = ϕ
0
(y
i,j−2
) = 1
ϕ
0
(y
i,j−1
) = ··· = ϕ
0
(y
i,k−3
) = 0
ϕ
0
(z
j
) = 1 (j−1) C
i
ϕ
0
(y
i,r
) = 1
r = 1, . . . , j − 2 r C
i
ϕ
0
(y
i,s
) = 0 y
i,s
= 1 (s+1) C
i
s = j−1, j, . . . , k−3 ϕ
0
k −2
C
i
ϕ
0
(C
i
) = 1
⇐ ϕ
ϕ(F
i
) = 0 ϕ
0
ϕ ϕ
0
(C
i
) = 1
ϕ(F
i
) = 0
ϕ(z
1
) = ϕ(z
2
) = ···ϕ(z
k
) = 0.
C
i
y
i,1
= 1
ϕ
0
(y
i,1
) = 0 C
i
ϕ
0
(y
i,2
) = 1
k−3 C
i
ϕ
0
(y
i,1
) = ϕ
0
(y
i,2
) = ··· = ϕ
0
(y
i,k−3
) = 1.
ϕ
0
(y
i,k−3
) = 0 ϕ(z
k−1
) = ϕ(z
k
) = 0 y
i,k−3
∨
z
k−1
∨ z
k
C
i

ut
• VC ≤
p
CLIQUE
• 3 SAT ≤
p
VC
NP
3000 NP
P NP
NPO
U = (Σ
I
, Σ
O
, L, M, cost, goal) ∈ NPO
L ∈ P
{ x ∈ Σ
∗
I
U.}
p
U
x ∈ L y ∈ M(x) |y| ≤ p
U
(|x|)
{
.}
A y ∈
Σ
∗
O
x ∈ L |y| ≤ p
U
(|x|) y ∈ M(x)
cost
U NPO
•
U U
(Σ
I
, L)
•
U (Σ
O
, M(x))
x
•
U
NPO VP
33

• U
• U
U
NPO
MAX SAT
• x ∈ Σ
∗
logic
• x Φ
x
α ∈ {0 , 1}
∗
|α| < |x|
|α|
Φ
x
•
Φ
x
|x|
MAX CUT
G = (V, E) 2
G = (V, E) (V
1
, V
2
)
V
1
∪ V
2
= V, V
1
∩V
2
= ∅,
V
1
V
2
cost (V
1
, V
2
) = |E ∩ {{v, u} | v ∈ V
1
, u ∈ V
2
}|.
MIN VC
G = (V, E)
MAX CUT MIN VC NPO
PO
P
PO
U = (Σ
I
, Σ
O
, L, M, cost, goal) ∈ PO
• U ∈ NPO
• A
x ∈ L A(x)
