Горбунов Л.В., Бучацкий Л.П. Метод моделирования биологического эксперимента

Подождите немного. Документ загружается.

Л.В. Горбунов, Л.П. Бучацкий

МЕТОД МОДЕЛИРОВАНИЯ

БИОЛОГИЧЕСКОГО

ЭКСПЕРИМЕНТА

Рекомендации

Киев - 2004

УДК.591.15.16.+578.087.1

Рекомендации подготовили: Л.В. Горбунов, Л.П. Бучацкий.

В методических указаниях представлена структурная схема,

отражающая поэтапный процесс проведения моделирования

эксперимента, от постановки задачи на исследования до

математического обобщения полученного результата. Представлены

формулы получения достоверного научного результата при

минимальном количестве измерений. На примерах показано, что

повышение эффективности исследовательской работы связано с

моделированием проведения эксперимента основанном на

минимизации затрат времени и средств.

Рекомендовано для биотехнологов, животноводов, зоотехников

и ветеринаров, а также студентов биологических специальностей,

факультетов ветеринарной медицины и зооинженерии при

выполнении курсовых и дипломных работ.

Введение

Многие биологические исследования, традиционным образом,

проводятся эмпирическим способом, то есть посредством последо-

вательного перебора возможных вариантов. Проведение экспери-

мента без должного его планирования приводит исследование к

крайности - "ползучему эмпиризму". Такой подход требует большо-

го количества проведения опытов и как следствие - значимых

потерь времени и материальных средств. Кроме того, решение

проблемных задач не всегда осуществимо стандартными методами.

Применение моделирования, в качестве инструмента познания,

повышает эффективность данного процесса посредством перехода к

полуэмпирическим поискам. Эффективный процесс исследования,

как и обучения, включает в себя модель как элемент теоретической

части работы и эксперимент - практической. Моделирование не

может и не должно быть альтернативой проведения эксперимента, а

является его необходимым дополнением. Построение модели без ее

последовательной экспериментальной проверки приводит к другой

крайности в исследовании - "слепому академизму".

Повышение эффективности процедуры исследования заключа-

ется в расширении диапазона применяемых методов от его теорети-

ческой части до экспериментальной. Раскрытие диапазона исследо-

вания обеспечивает высокую эффективность данного процесса

только при условии баланса теоретической и практической его

части. В противном случае исследование будет сводиться к одной из

его крайностей. Под проведением комплексного исследования пони-

мается весь спектр мероприятий от постановки задачи на исследо-

вание до получения математической модели изучаемого явления.

Далеко не каждый исследователь видит необходимость в доведении

своей работы до уровня математической абстракции. Однако не

следует забывать, что именно математические модели являются

мощным инструментом, как описания, так и анализа полученных

данных. Уровень завершенности работы определяется степенью

адекватности описания изучаемых явлений с возможностью их по-

следующего объяснения. Математическое абстрагирование полу-

ченных результатов может способствовать разрешению проблемы

не повторяемости экспериментальных данных при изменяющихся

условиях проведения опытов и служить отправным моментом про-

ведения дальнейших исследований. Хотя рекомендаций, позволяю-

щих проводить подобного рода обобщения, достаточное количество

[1, 2, 3, 4], алгоритмов связывающих в единую цепь, процесс от

планирования эксперимента до построения аналитической модели, в

доступной нам литературе пока ещё нет. В данной работе сделана

попытка собрать воедино все то, что может помочь начинающему

исследователю понять структуру исследования и реализовать

максимально обобщенный результат.

1. Этапы построения модели

биологического эксперимента

Поскольку исследование начинается с создания модели прове-

дения эксперимента, то естественен и приоритет ее построения над

практической частью работы. Построение и совершенствование

модели осуществляется ступенчато от формулировки рабочей

гипотезы, и ее проверки в ходе проведения экспериментальной

работы, до обобщения полученных результатов до уровня

математического абстрагирования (таблица 1).

Первым этапом построения модели является установления воз-

можности решения задачи, посредством построения рабочей гипо-

тезы, при условии её не решённости к настоящему времени. Прове-

дение моделирования исследования позволяет установить не только

возможность решения данной задачи, но и определить условия,

обеспечивающие минимальные затраты для разрешения постав-

ленной проблемы. Наиболее простой формой модели эксперимента

является план его выполнения. Для этого необходимо определить

целевую функцию, численно отражающую поставленную цель

исследования и параметры, определяющие развитие изучаемого

явления.

Целевая функция определяет факторы, обуславливающие

развитие изучаемого явления. В общем, виде это можно представить

таким образом: С(щ, в,, где: С - целевая функция, числено

отражающая поставленную цель исследования, а,, $ - параметры,

определяющие развитие изучаемого явления. Поддающиеся

изменениям в ходе эксперимента - а

неподдающиеся изменениям -

неопределяемые изменения - с!|. При разработке целевой функции

устанавливают независимые переменные (аргументы ЬД

определяющие изменение зависимой переменной (функции С). В

опытах измеряют характеризующие как факторы (аргументы Ь ).

так и показатели развития явления (целевую функцию С) [5].

Габлица 1. Структу

рная схема построения модели эксперимента

№

Этапы

выполнения

Способ

выполнения

Результат

Постановка

цели

литературный

поиск

не решенность

проблемы

Постановка

цели

рабочая гипотеза

возможность решения

Определение

параметров

составление

целевой функции

план выполнения

Выбор методов

измерения

абсолютная,

относительная

величина

Выбор методов

вычисления

кач- количественный

статистический

анализ

Решение задачи

схема опыта

таблица

Решение задачи

поисковый опыт

оптимизация 1-3

этапов

Решение задачи

основной

эксперимент

графическая

зависимость

Анализ и

обобщение

результатов

описание,

прогноз

регрессионное

уравнение

Анализ и

обобщение

результатов

поиск причинно-

следственной

связи

аналитическое

уравнение

Следующим этапом моделирования исследования является

выбор методов измерения и обработки полученных результатов.

При всем разнообразии методов исследовательской работы задача

моделирование эксперимента сводится к тому, чтобы при возможно

минимальных объемах наблюдений получать достаточно полную

информацию об изучаемых объектам Планирование эксперимента

основывается на установленной надежности, которая обеспечи-

вается за счет увеличения количества измерений и уменьшения их

погрешностей. Общая величина погрешности эксперимента состоит

из погрешностей, возникающих при проведении отдельных опытов,

которые складываются из ошибок отдельных измерений.

При проведении измерений предпочтительно регистрировать не

только полученные абсолютные значения исследуемых параметров

4 но и в отдельных случаях переводить их в относительные

величины. Относительные показатели дают возможность сопостав-

лять измеренные величины, имеющие различные размерности, как

это показано в нижеприведенных формулах, и переходить к относи-

тельной системе координат. Например, подобным образом осущест-

влена оценка влияния индивидуальных свойств деконсервирован-

ных ооцитов и эмбрионов млекопитающих на уровень их

сохранности и установлен верхний порог данного показателя [6].

2. Планирование проведения

биологического исследования

При всем разнообразии методов исследовательской работы

шдача планирования эксперимента сводится к тому, чтобы при

возможно минимальных объемах наблюдений получать достаточно

полную информацию об изучаемых объектах. Планирование

эксперимента основывается на установленной надежности, которая

обеспечивается за счет увеличения количества измерений и

уменьшения их погрешностей. В некотором смысле эта задача

является как бы обратной той, которая решается при статистической

обработке результатов уже завершенных экспериментов.

Представленные в литературе формулы оценки оптимального числа

измерений имеют значительное численное расхождения [1, 3, 4].

Очевидно, что данные расхождения объясняются допущениями,

вводимыми авторами в ходе вывода конечных формул.

Количественная взаимосвязь представленных параметров выражена

в предлагаемых формулах.

2. /. Определение минимального количества измерений,

обеспечивающего достоверный научный результат

для одной выборки

Как показывает опыт, нет необходимости в повышении

точности измерений, когда такая степень точности не требуется.

Данное положение относится и к измеряемым объектам, и к

вычислениям, обобщающим статистические характеристики.

Точность измерений и их последующих вычислений определяется

установленной степенью надежности предполагаемых результатов.

Значения заданных надежностей, т.е. вероятностей реализаций

данных событий представлены в таблице 2 [2, 3].

Таблица 2. Требуемые уровни надежности, связанные с

проведением конкретного рода исследования

Вероятность заданного

уровня Р/

Величина вероятности

0,68

0,95

Уровень значимости

оценок - р

0,99

0,999

0,32 0,05

0,01

0,001

Р1 - вероятность приемлемая для поисковых опытов; Р

- для

биологических исследований; Р

3А

- для исследований, связанных со

здоровьем человека.

Доверительная вероятность - Р

связана с уровнем значимости

оценок измерений - р [5], и равна ее относительной погрешности

1-Р:

где: М - среднее арифметическое, А - доверительный интервал [1,

2, 3],

А=Ш, (2)

где: т - ошибка среднего квадратического отклонения, / - критерий

Стьюдента.

Установленная надежность накладывает условия на общую

величину погрешности эксперимента, которая не должна превышать

требуемый уровень значимости. Общая величина погрешности

эксперимента состоит из погрешностей, возникающих при

проведении отдельных опытов, которые складываются из ошибок

отдельных измерений. Для установления предельно допустимой

величины погрешности эксперимента необходимо определить его

общий доверительный интервал и, оценив необходимое количество

измерений, понизить величину погрешности до требуемого уровня

значимости. Выбор величины доверительной вероятности является

отправной точкой планирования эксперимента. Установив в ходе

поискового опыта основные статистические величины изучаемых

явлений, такие как среднее арифметическое и среднеквадратйческое

отклонение, можно приступать к планированию эксперимента.

Оптимальная схема исследования основана на проведении

минимального количества измерений при обязательном условии

получения достоверного результата. Необходимая численность

выборки п, отвечающая точности получения среднего результата,

зависит от величины ошибки выборочной средней и выводится из

формулы вычисления средней квадратической ошибки среднего

арифметического - т [1,2,3].

где: а - среднее квадратическое отклонение, откуда

7(4)

\tMmj

домножив и разделив данное выражение, приведенное в скобках, на

среднюю величину - Ми критерий Стьюдента - (, произвели замену

второго сомножителя на р

, согласно формулам 1 и 2, и третьего

сомножителя на коэффициент вариации - С

Л4а)

Для уровня надёжности Р=0,95 и величины критерия

Стьюдента 1=2, соответствующего достоверной выборке (п>30),

значение формулы упрощается:

п=0.1бСу, (46)

Значения численности выборки, основанной на нормальном

законе распределения признаков и имеющей количественную

градацию в зависимости от коэффициента вариации при уровне

надёжности представлены в таблице - 3.

Таблица 3. Значение минимального объема выборки п в

зависимости от коэффициента вариации для количественного

анализ

при

Р=0,91

100

32 64

100

144

256

400

1600

Пример. В случае если величина среднеквадратического

отклонения исследуемого нами признака равна пяти (о=5), а

среднее арифметическое двадцати ^М=20), коэффициент вариации

для данной выборки составляет двадцать пять процентов

(С

=(5/20) 100=25%). Тогда минимальное количество измерений,

обеспечивающее достоверный результат с уровнем надежности

(Р=0,95)

равно сто. (п=0.16х25

=100).

При альтернативной группировке данных, основанных на

биномиальном распределении признаков и не имеющих

количественных градаций, когда численность выборочных групп

выражается в долях единицы, планируемый объем наблюдений

определяется следующим образом:

„

0.16С^0.1^Щ

(})

где: Ч¥-вероятность, величина, определяемая как отношение числа

случаев, при которых это событие произошло к общему числу

наблюдений К' Т¥~ и у = ^ЩТ^Щ [3, 4], тогда:

п = 1600— г— = 1600

, (5а)

Для выборки, основанной на биномиальном законе

распределения признаков и не имеющей количественной градации,

при уровне надёжности Р=0.95, оптимальное количество измерений

представлено в таблице 4.

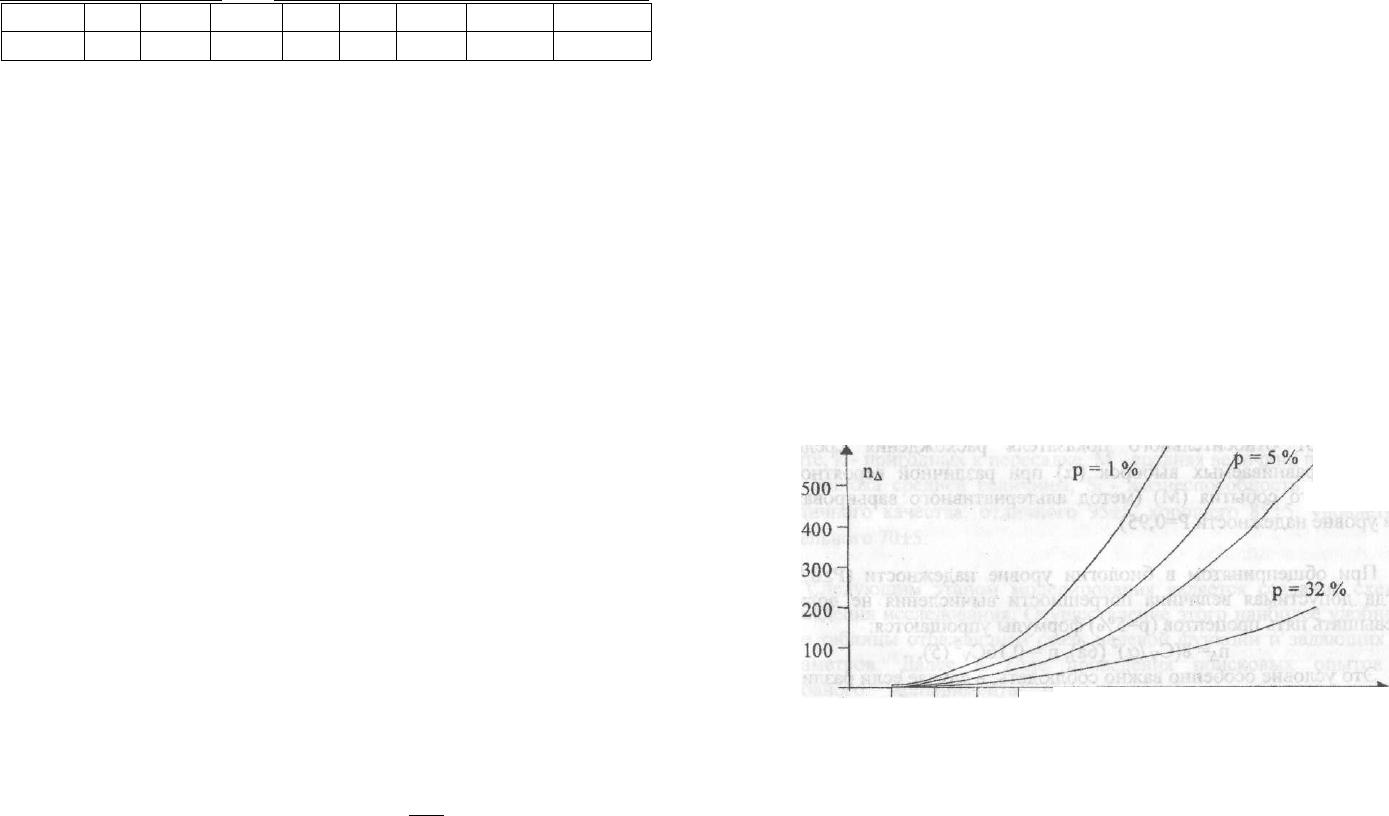
Таблица 4. Значение минимального объема выборки п в

зависимости от средней вероятности М для качественного анализа

при уровне надёжности Р=0,95

М(%)

95 90 85 80

70 60

N 16 89 178 285 400

533

686

1067

Пример. В случае если вероятность изучаемого нами признака

составляет восемьдесят пять процентов (М=85%), то величина

среднеквадратического отклонения для данной выборки составит

около тридцати шести измеряемых единиц (о=35,7). Таким образом,

необходимо провести не менее двухсот восьмидесяти пяти

измерений, чтобы получить достоверный результат с заданным

уровнем надёжности (я=1600(15/85)=285).

Обобщая полученные результаты, можно сделать следующее

заключение: для уменьшения ошибки выборочной средней в К раз

нужно увеличить объем выборки в К

раз. Если величина

количества измерений, обеспечивающего требуемую достоверность

значения, настолько велика, что её невозможно реализовать на

практике, то в отдельных случаях следует планировать опыт,

основываясь на оценке достоверности различия средних значений

контроля и эксперимента.

2.2 Определение минимального количества измерений,

обеспечивающего достоверный научный результат

при сравнении двух выборок

Минимальное количество измерений, обеспечивающих

достоверный результат, зависит от выбора метода проведения

статистического анализа и от способа проверки полученного

результата. Если полученный результат планируется сравнивать с

данными, полученными в контроле при выполнении данного

эксперимента, то необходимое количество измерений (п

) в каждой

выборке можно определить из следующих формул:

-М

ДМ ДМ а

I = ^»-у=, т =

— =

фп? + т\ У 2га

* • 42 4п

п =

дм

Г-л/2чт-100

•100%, а =

ДМ

= 2(Г-С,/а)

дм-юо

100%, п

= 2 (г Су/а)

(6),

м м

где: Су - коэффициент вариации выборки, а - относительный

показатель расхождения средних величин сравниваемых выборок,

X - критерий Стьюдента {1,00; 1,66; 1,98; 2,63} для уровней

надежности Р{0,68; 0,90; 0,95; 0,99} при допустимых величинах

погрешности вычисления р{0,32; 0,10; 0,05; 0,01}, соответственно.

Данная формула ф(6) позволяет установить минимальное

количество измерений по каждой из сравниваемых выборок.

Значимая вариация биологических параметров (Су>10Уо)

приводит к необходимости проведения большого количества

повторов измерений (п) с целью получения достоверного результата

(рис. 1). Если для количественного метода статистического анализа,

как правило, достаточно малой выборки (п<30 для Су» 10-5-15%), то

для качественного (метод альтернативного варьирования)

р =10 %

0,5 1 2 3 4 5 6 7 8 9 10 Су/а

Рис. 1. Зависимость минимального количества измерений необхо-

димых для получения достоверности различия двух сравниваемых

выборок от соотношения показателей коэффициента вариации (Су)

и относительного показателя расхождения средних величин

сравниваемых выборок (а) при различных допустимых величинах

погрешности вычисления (р).

количество повторов необходимо значимо больше (п>100 для

«35-^300%, при вероятности полученного результата

М«90( 10)^50%, соответственно) (рис. 2).

10 20 30 40 50 60 70 80 90 100 М,%

Рис. 2. Зависимость минимального количества измерений необхо-

димых для получения достоверности различия двух сравниваемых

выборок от относительного показателя расхождения средних

величин сравниваемых выборок (а) при различной вероятности

реализуемого события (М) (метод альтернативного варьирования

при уровне надежности Р=0,95)

При общепринятом в биологии уровне надежности (Р>0,95),

когда допустимая величина погрешности вычисления не должна

превышать пять процентов (р=5%) формулы упрощаются:

= 8(С

/а)

(6а), п = 0,16С

(5).

Это условие особенно важно соблюдать, в случае если различие

между сравниваемыми выборками составляет больше семи

процентов (ос>7, п

<п).

Предпочтительно использовать количественный статистический

анализ в сопоставлении с качественным [7]. Использование

количественного метода статистической обработки для оценки

жизнеспособности эмбрионов млекопитающих дает возможность

снизить количество измерений более чем в десять раз, по сравнению

с качественным методом, за счет уменьшения величины ошибки

среднеквадратического отклонения при условии получения

достоверного результата (табл. 5).

Таблица 5. Способы оценки технологии криоконсервации

эмбрионов крупного рогатого скота при помощи различных методов

статистического анализа. .

Качественный

Количественный

Показатели

биообъекта

Сохранность

=к/п, %

Жизнеспособност

ьБ = 5.,%

П 1

Выживаемость

М±т для

п-10

«о

М±т для

п=10

М±т для

п=10

Свежепо-

лученного

100±0

90±1,7

Деконсерви

рованного

178

90±9,5

88,5±1,8

98,3±1,5

Культиви-

рованного

400

80±12,7

86±1

96,6±1,6

- количество измерений необходимое для получения досто-

верного среднего значения; п - количество эмбрионов в данном

опыте, к - пригодных к пересадке, М - средняя величина показателя;

т - ошибка средней величины, $1 - жизнеспособность эмбрионов

различного качества: отличного 95±5, хорошего 85±5, удовлетво-

рительного 70±5.

Следующим этапом моделирования является создание схемы

проведения исследования. Осуществление этого наиболее удобно в

виде таблицы отражающей связь целевой функции и задающих ее

параметров. Далее в ходе проведения поисковых опытов и

основного эксперимента осуществляется заполнение данной

таблицы, что дает возможность установить характер связи между

функцией и ее аргументом на основании чего построить

математическую зависимость. Установив в ходе поискового опыта

основные статистические величины изучаемых явлений, такие как

среднее арифметическое и среднеквадратическое отклонение,

можно приступать к моделированию эксперимента.

Убедившись в возможности реализации необходимого

количества измерений в данном планируемом эксперименте, в ходе

выполнения 1-ї-З этапов построения его модели, можно приступать к

проведению основных опытов. Моделирование основного

эксперимента в ходе проведения поисковых опытов позволяет

исследователю получить при завершении работы достоверный

научный результат.

3. Способы обобщения результатов полученных

в ходе проведения биологического исследования

Для универсального оперирования полученной информацией

необходимо обобщать экспериментально полученные данные до

уровня математического абстрагирования. Обобщение результатов

эксперимента, полученных в различных опытах, проводят при помо-

щи вычисления величин: М - среднее арифметическое, <Т- средне-

квадратическое отклонение, С

- коэффициент вариации, которые

удобно выражать через моменты Ь-го распределения - Мь а степень

их достоверности через величину ошибки репрезентативности - т

(см табл. 6). Необходимым условием правомерности использования

этих параметров является нормальность распределения изучаемых

выборок, критериями, определения которых служат: коэффициент

асимметрии распределения - А

и коэффициент эксцесса - Ех. Для

избежания получения искажения объективной информации также

необходимо исключить грубые ошибки, которые возникают при

проведении измерений. Численным показателем достоверности

текущего значения - х^ а также достоверности конкретной выборки -

^ является критерий Стьюдента - 1:

(р,п).

В случае, если исследователь наблюдает расхождение двух

величин целевых функций С, полученных при измерении

изучаемых факторов а

то достоверность данного расхождения

можно подтвердить при помощи критерия Стьюдента - %І.

Общим принципом чистоты проведения исследования является

постоянство всех остальных факторов при изменении избранных а^

Тестом на соблюдение выше приведенного условия является

критерий равноточное™ измерений. Равноточность измерений

серии опытов позволяет обобщить результаты различных

Таблица 6. Получение основных статистических параметров и кри-

териев их достоверности, выраженных через моменты распределения.

момент п-го

распределения

N1^0= X среднее

арифметическое

дисперсия

А=^т (0,2<А

<0,

5) коэффициент

асимметрии

= ^-3

х а

коэффициент эксцесса

(Ех « 3, условие нормаль

ности распределения).

»2 = -^

статистическая ошибка

Х)

= Д- коэффициент

вариации.

Рас

ИтерИЙ

Фишера

771 ^ —ошибка

репрезентатив-

ности

?П =

Тп

т.

ЛІСУ

2т

2п

С,

2п

г =

ас

5>А

коэффициент корреляции

*^ас ас <у

коэффициент регрессии

э1

(р,п) критерий Стьюдента

(критерий достоверности)

- текущего

Значения. Если 1,>3, то х

не принадлежит данной

выборке

достоверность конкретной

выборки. Если Ір > І

8І

то Н

=0 данное

распределение

Принадлежит

генеральному, при

заданном уровне

надежности - р

(а - уровень значимости

выборки).

/ — __

V .:,

л/т

+пг +2гпгт

достоверность различия

двух выборок.

Если Ь

> Ь

, то Но Ф 0

- данные распределения не

принадлежат генеральному.

Примечание: Н

- нулевая гипотеза, (предполагает принадлежность

данного распределения генеральному Н

=0).

экспериментов и уменьшить суммарные ошибки исследования.

Показателем равноточное™ опытов является критерий Фишера - Р.

Далее экспериментальные данные обобщают в такой последова-

тельности: находят функциональные связи изучаемых явлений,

устанавливают основные закономерности, математически выра-

жают, раскрывают их физическую сущность с целью последующего

теоретического развития. К обобщению следует привлекать

материалы других исследований, из которых по каким-либо

причинам не сделаны должные выводы. Функциональные связи

легче выявить, если данные опытов представить в виде графиков.

В практике сельскохозяйственных и биологических исследова-

ний часто возникает необходимость изучить характер связи между

двумя (или более) варьирующими признаками. Ковариационный

анализ направлен на установление сопряженности вариационных

связей и объединяет в себе ряд относительно самостоятельных

методов: дисперсионный, корреляционный и регрессионный анали-

зы. Дисперсионный метод основан на разложении общей дисперсии

статистического комплекса на составляющие ее компоненты,

сравнивая которые друг с другом посредством ^-критерия, можно

определить, какую долю общей вариации учитываемого

(результативного С/) признака обуславливает действие на него как

регулируемых а

так и не регулируемых в опыте факторов 6

Задача исследователя при проведении корреляционной связи -

определить характер и измерить тесноту сопряженности между

признаками, из которых один является факториальным а

а второй

результативным С. Зависимость между переменными величинами щ

и С может быть описана разными способами. В частности, любую

форму связи можно выразить уравнением общего вида С^/(а^ где С

рассматривают в качестве зависимой переменной, или функции от

другой - независимой переменной величины а

называемой

аргументом [5].

Вывод эмпирических формул проводится на основе

экспериментально полученной функциональной зависимости,

объясняемой в общем, виде. Подбор типа эмпирической формулы

для определения ее параметров используется на основе

регрессионного анализа. Построение регрессионной зависимости

осуществляется при помощи использования специальных

прикладных программ разработанных для ЭВМ. Полученное

эмпирическое выражение можно представить в полуаналитическом

или чисто аналитическом виде. Иногда сама структура

эмпирической формы указывают на пути превращения в

аналитическую формулу. Под аналитическими уравнениями следует

понимать такие, в которых все основные члены имеют размерность

и логично вытекают из законов физики.

Наличие аналитического выражения зависимости целевой

функции от ее аргументов, позволяет использовать его как

математическую модель. Очевидно, что исследование считается

законченным, если достигнута его цель. Если реализация цели

заключена в нахождении максимальной или минимальной величины

целевой функции, то построение математической модели,

отражающей природу взаимосвязи между целевой функцией С и ее

аргументами а

В1 и 4, является наиболее приемлемым способом

нахождения оптимальных значений изучаемых факторов а

{

мак

— Р

(а* опт, В]). Математические модели строятся на основе полученных

эмпирических и рациональных формул, а поэтому их удобно

разделять на описательные и объяснительные.

Математические модели являются мощным инструментом, как

описания так и анализа полученных данных. Ценность модели

определяется степенью адекватности описания изучаемых явления и

возможностью их объяснения. Математическое абстрагирование

полученных результатов способствует разрешению проблемы не

повторяемости экспериментальных данных при изменяющихся

условиях проведения опытов и служит отправным моментом

проведения дальнейших исследований.

Наиболее ярким примером значимости математического моде-

лирования в решении прикладных задач являться работа П. Мейзура

[8]. Благодаря данной модели впервые удалось получить

жизнеспособное потомство от деконсервированных эмбрионов

млекопитающих после неудачно проведенных эмпирических

поисков на протяжении трех десятилетий.

Повышение эффективности исследовательской работы связано

с моделированием проведения эксперимента от постановки задачи

на исследования до математического обобщения полученного

результата. Предложенная структурная схема моделирования

эксперимента, позволяет получать достоверный научный результат

при минимальных затратах времени и средств. Далеко не перед

каждым исследователем предстает необходимость проводить работу

от постановки задачи до получения результатов в виде

математической модели. Однако большая часть проблем,

затронутых в данной работе, так или иначе, станут актуальными при

проведении любого, даже самого простого, эксперимента. Полагаем,

что для биологов представленная последовательность выполнения

комплексных исследований окажется наиболее удобной.

Литература

1. Веденяшш Г.В. Общая методика экспериментального

исследования и обработка опытных данных. М. Колос, 1965, 130 с.

2. Вознесенский В.А, Статистические методы планирования

эксперимента в технико-экономических исследованиях. М. 1981. 250 с.

3. Лакин Г.Ф. Биометрия. М. "Высшая школа" 1990 г. 306-310 с.

4. Горбунов Л.В. Определение минимального количества измерений,

обеспечивающего достоверный научный результат // Агроекологічний

журнал. - Київ. - 2002. - Випуск 1. -С. 69-71.

5. Горбунов Л.В. Способи узагальнення результатів отриманих при

проведенні експериментального біологічного дослідження // Рибне

господарство. Міжвідомчий тематичний науковий збірник. Київ. - 2001.

- Випуск 59-60. -С. 55-58.

6. Горбунов Л.В. Вплив біологічної різноякістності та варіації

технологічних параметрів на збереженість ооцитів і ембріонів ссавців при

кріоконсервації: Автореф. дис... на здобуття вченого ступеня кандидата

сільськогосподарських наук.- Харків.-1996.-23 с.

7. Горбунов Л.В. Кількісний спосіб оцінки життєздатності ембріонів

ссавців // Вісник Білоцерківського державного аграрного університету. -

Біла Церква.-2001.- №17.- С. 30-34.

8. Mazur P. Theoretical and experimental effect of cooling and warming

velocity on the survival of frozen and thawed cells.// Cryobiology.- 1966,- V.3.-

N2.- p.181-192.