Горбунов А.А. Информационные технологии. Методические указания к выполнению лабораторных работ

Подождите немного. Документ загружается.

щей команды «float (%pi/2), numer;» и ее выполнению. Результат

(1.570796326794897) отобразится в ячейке «%о2» (рис. 3.1).

Рис. 3.1. Вычисление π/2 в программе Maxima

2.2. Вычисление е

(е – основание натурального логарифма).

Процедура аналогична предыдущей. Используйте символ «%e».

2.3. Вычисление (π/2* е

– 5)/2+12.

Указанная задача должна быть решена с использованием двух способов

ввода данных (прямого и адресного). Прямой ввод был рассмотрен в п. 2.1 и

2.2.

Адресный ввод данных и команд аналогичен по сути указанию на вызов

процедуры при написании компьютерной программы. Применение такого спо-

соба эффективно в случае неоднократного использования каких-либо функций

и значений, а также при построении графиков, так как в строке ввода указыва-

ются не функциональные выражения, а адреса ячеек, их содержащие.

Пример адресного ввода с указанием на входные ячейки:

«левая скобка, адрес ячейки со значением π/2 (%i1), знак умножения (*), адрес

ячейки со значением е

(%i3), знак вычитания (–), число 5, правая скобка, знак

деления (/), число 2, знак сложения (+), число 12, enter» (рис. 3.2).

Рис. 3.2. Пример адресного ввода

Выполните адресный ввод с указанием на выводные ячейки и сравните

полученные результаты для разных способов задания.

Обратите внимание на представление данных и команд в основном

окне программы!!!

3. Определение функций и построение двумерных графиков.

3.1. Построение графика функции f(x)=3sin(x).

Существуют два способа построения графиков в программе Maxima.

1) На панели инструментов выберите вкладку «График 2D». В открыв-

шемся окне в поле «Выражение» введите «3*sin(x)» и задайте диапазон измене-

ния переменных х, у так, чтобы отобразилось два периода колебаний синусои-

ды. Выберите формат и дополнительные опции (set grid) графика, после чего

нажмите «OK» и получите график.

2) Второй способ связан с предварительным определением функции.

В строке ввода задайте функцию: «f(x):=a*sin(x)», затем определите ко-

эффициент а, записав «а:3». Присвоение функции в программе обозначается

«:=», а присвоение значения переменной или коэффициента «:». Откройте

вкладку «График 2D» и в поле «Выражение» введите «f(x)», настройте осталь-

ные параметры и получите график, идентичный первому.

Maxima позволяет выбирать формат представления графиков: (по умолча-

нию (gnuplot), встроенный, openmath). Формат gnuplot, принятый по умолча-

нию, удобно использовать для определения мгновенных значений функций, так

как в окне графика имеется измерительный курсор. Встроенный формат позво-

ляет сохранить изображение в известных графических форматах (BMP, JPG и

др.) для дальнейшей обработки. Openmath требует наличия дополнительного

программного обеспечения, без которого не функционирует.

При многократном построении графика, заданного одной и той же

функцией, в целях экономии времени воспользуйтесь опцией «Копировать

текст» контекстного меню.

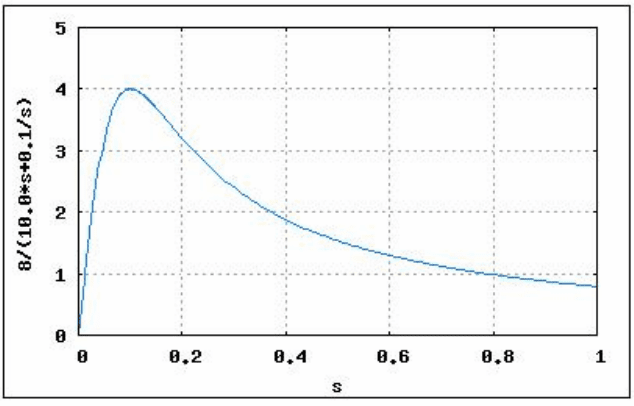
3.2. Построение статической механической характеристики асинхронного

двигателя

M(s)=2M

/(s/s

/s)

в диапазоне скольжения от 0 до 1.

Параметры асинхронного двигателя: M

=4 Нм, s

=0.1. Для данного экспе-

римента использовать предварительное определение функции.

Рис. 3.3. Механическая характеристика асинхронного двигателя

4. Построение трехмерных графиков.

4.1. Постройте график функции

49),(

yxyxz

−−=

Откройте вкладку «График 3D», в графе «Выражение» введите предва-

рительно заданную функцию, выберите формат графика и настройте подходя-

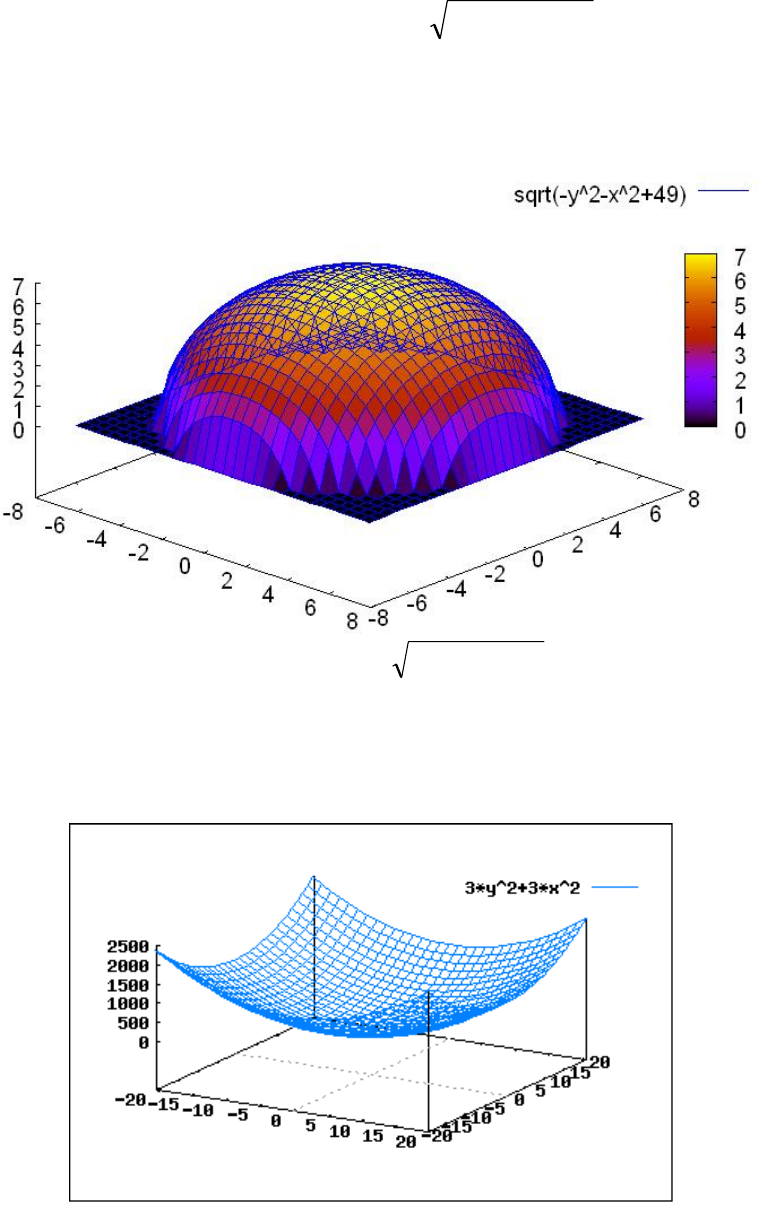
щий масштаб. Как показывает рис. 3.4, рассматриваемая функция описывает

полусферу.

Рис. 3.4. График функции

49),(

yxyxz

−−=

в формате gnuplot

4.2. Постройте график функции

33),(

yxyxz

Результат приведен на рис. 3.5.

Рис. 3.5. График функции

33),(

yxyxz

во встроенном формате

Рассматриваемые графики представлены в декартовой системе коорди-

нат, однако для построения пространственных поверхностей рациональнее ис-

пользовать цилиндрическую и сферическую системы координат, которые вы-

бираются в окне «График 3D».

5. Дифференцирование и интегрирование.

5.1. Вычислите значение производной функции f(x)=x

+3x

-2x+cos(x

) в

точке x=7.

Сначала определите функцию f(x), затем вызовите процедуру дифферен-

цирования «Анализ/дифференцировать» или воспользуйтесь контекстным ме-

ню. Получившееся выражение (производную) присвойте новой функции, на-

пример у(х), укажите значение аргумента «x:7», и в строке ввода наберите «у(х)

enter». Результат составит 1425.352537138633.

5.2. Интегрируйте функцию g(t)=(5t

+1)/t

Операция интегрирования осуществляется с помощью процедуры «Ин-

тегрировать» в разделе «Анализ».

5.3. Интегрируйте функцию f(x)=(x

-x+1)/(x

+1).

Проверьте правильность вычислений, взяв производную от полученного

выражения. Если результирующая функция не соответствует исходной, попро-

буйте ее «упростить», «раскрыть» или «упростить рационально».

Рассмотренные задачи интегрирования и дифференцирования являются

примерами аналитических (символьных) вычислений, реализация которых воз-

можна лишь средствами интеллектуальной системы. В случае, если Maxima не

справляется с аналитическими вычислениями (ввиду чрезвычайной сложности

задачи), применяют численные методы расчета.

6. Решение уравнений.

6.1. Определите корни системы уравнений (3.1) и выполните проверку

решения.











=++

=+−

=−+

2232

zyx

(3.1)

Корни систем уравнений определяются при помощи специальной проце-

дуры «Решить алгебраическую систему» раздела «Уравнения». В окне последо-

вательно задается количество уравнений, их вид и неизвестные переменные.

Уравнения могут быть заданы в том виде, как они записаны в (3.1) (естествен-

но, с учетом знаков умножения между переменными и коэффициентами).

6.2. Определите корни системы уравнений (3.1) методом определителей.

Корни уравнений определяются следующим образом:

∆∆=

, (3.2)

где

∆

– определители, вычисляемые для данной системы как:

113

232

121

−

=∆

118

232

122

−

=∆

183

222

121

−

=∆

813

232

221

−=∆

. (3.3)

Реализация этого метода в Maxima потребует сформировать 4 матрицы и

рассчитать их главные определители. Задайте матрицу «М» в строке ввода:

«M:matrix([1,2,-1],[2,-3,2],[3,1,1];» и рассчитайте ее определитель («Алгеб-

ра/определитель»). С остальными поступаем аналогично. Сравните результат с

полученным в п. 6.1.

6.3. Достаточно часто в учебной, научной и инженерной сферах деятель-

ности приходится выполнять арифметические действия над массивами чисел

(векторами и матрицами), поэтому в качестве задания выполните умножение

двух матриц 2

2, выданных преподавателем, в Maxima и вручную по формуле

(3.4). Сравните результат.

5838

1810

86253645

82213241

×+××+×

=×

. (3.4)

Допускается перемножение матриц размерностей [m

p]. В

программе Maxima для перемножения матриц используется особый знак

«.» – десятичная точка. Использование знака «*» даст неверный резуль-

тат.

6.4. Решение трансцендентного уравнения.

Только для простейших уравнений удается найти решение в аналитиче-

ском виде, то есть записать формулу, выражающую искомую величину х в яв-

ном виде через параметры уравнения. В большинстве же случаев такие задачи

приходится решать численными методами.

Численное решение обычно проводят в два этапа. На первом этапе необ-

ходимо отделить корни уравнения, то есть найти такие интервалы изменения

переменной x, где расположен только один корень. Для этого используют, в ос-

новном, графический или табличный метод, в соответствии с которым с задан-

ной точностью по точкам строится упрощенный график функции. На втором

этапе проводят уточнение отделенных корней, для этого используют богатый

набор известных алгоритмов и программ, создание которых возможно, напри-

мер, в среде Turbo Pascal. Программа Maxima обладает широкими возможно-

стями для численного решения сложных уравнений.

Требуется решить уравнение

)sin(8420)cos(3

xxxxx

+−=−+

. Для от-

деления корней представьте исходное уравнение в стандартной форме

0)sin(8420)cos(3

=−+−−+

xxxxx

, затем постройте график левой части

уравнения, записанного в стандартной форме. Точки пересечения графика с

осью абсцисс – корни уравнения. Зная диапазоны нахождения корней, вызовите

процедуру «Решить численно» и внимательно заполните соответствующие по-

ля. Проверьте правильность методом подстановки.

Повторите решение исходного уравнения, задав такой диапазон измене-

ния переменной x, в котором содержатся все корни. Каков будет результат?

Содержание отчета

1. Цель работы.

2. Функция и график механической характеристики двигателя.

3. График и решение для трансцендентного уравнения.

4. Подробное описание всех использованных в работе команд и процедур.

5. Выводы по работе.

Контрольные вопросы

Для успешной сдачи лабораторной работы студент должен знать от-

веты на представленные ниже вопросы, уметь решать практические задания,

схожие по своей сути с рассмотренными в лабораторной работе, и предста-

вить отчет, выполненный в соответствии с требованиями.

1. Поясните назначение и возможности программы Maxima.

2. Чем отличаются символьные и численные вычисления?

3. Чем отличаются математические программы Maxima и МВТУ?

4. Опишите интерфейс СКМ Maxima.

5. Как реализуется ввод данных и команд в рассматриваемой СКМ?

6. Что представляют собой и как решаются трансцендентные уравнения?

7. Как в программе реализуется построение графиков?

8. Назовите основные признаки, по которым Maxima может быть отне-

сена к экспертным системам.

9. Чем отличаются процедуры: «упростить», «раскрыть», «упростить ра-

ционально»?

10. Какие форматы представления графиков использует программа?

11. Какие процедуры и команды используются для решения систем урав-

нений?

12. Назовите известные вам команды.

13. Приведите примеры двух способов задания матриц в Maxima.

14. Чем отличаются прямой и адресный способы ввода команд и данных?

15. Назовите известные графические оболочки Maxima.

ЛАБОРАТОРНАЯ РАБОТА № 4

Выполнение чертежа электрической схемы в пакете sPlan (Demo)

Цель работы

1. Изучение функциональных возможностей графического пакета sPlan.

2. Получение практических навыков работы с данным пакетом в результате

выполнения чертежа принципиальной электрической схемы в соответст-

вии со стандартами ЕСКД.

Программа sPlan, разработанная и поддерживаемая фирмой «ABACOM

Ingenieurgesellschaft» (www.abacom-online.de), представляет собой удобный ин-

струмент для создания и редактирования чертежей электронных и электриче-

ских схем. Интерфейс sPlan прост и интуитивно понятен. Имеется обширная

библиотека схемных компонентов (резисторов, транзисторов, логических эле-

ментов и др.), условные графические обозначения которых соответствуют как

зарубежным, так и российским стандартам (ЕСКД). Для удобства пользовате-

лей и повышения эффективности компьютерного черчения существует множе-

ство инструментов разработки и редактирования, таких как автонумерация и

настройка элементов, регулируемая сетка, масштабирование и т. д. Процесс

создания чертежа схемы предусматривает последовательное выполнение сле-

дующих этапов:

1. Настройка формата листа (А1, А4 и др.) и шага сетки;

2. Выбор элементов из библиотеки, расположение в соответствии с эски-

зом и соединение их с помощью соединительных линий;

3. Выполнение необходимых обозначений и нумерации (автонумерации)

элементов; добавление в схему пояснительных надписей и комментариев при

необходимости.

Чертежи могут быть экспортированы в различные графические форматы

(BMP, JPG, GIF) для последующей обработки или напечатаны непосредственно

из sPlan.

Общие требования к выполнению схем

1. Схемы выполняют без соблюдения масштаба и действительного про-

странственного расположения составных частей изделия.

2. Необходимое количество типов схем, разрабатываемое на проектируе-

мое изделие, а также количество схем каждого типа определяется разработчи-

ком в зависимости от особенностей изделия. Комплект схем должен быть по

возможности минимальным, но содержать сведения в объеме, достаточном для

проектирования, изготовления, эксплуатации и ремонта изделия. Между схе-

мами одного комплекта конструкторских документов на изделие должна быть

установлена однозначная связь, обеспечивающая возможность быстрого полу-

чения необходимой информации об элементах, устройствах и соединениях на

всех схемах данного комплекта.

3. На схемах, как правило, используют стандартные условные графиче-

ские обозначения. Если необходимо использовать нестандартные обозначения

некоторых элементов, то на схеме делают соответствующие пояснения.

4. Следует добиваться наименьшего числа изломов и пересечений линий

связи, сохраняя между параллельными линиями расстояние не менее 3 мм.

5. На схемах допускается помещать различные технические данные, ха-

рактеризующие схему и ее элементы. Эти сведения помещают либо около гра-

фических обозначений, либо на свободном поле схемы, как правило, над ос-

новной надписью.

6. Разрешается выполнять схему на нескольких листах (объединенную

или комбинированную схему).

Содержание работы

1. Ознакомьтесь с интерфейсом графического пакета sPlan. Изучите со-

держание библиотеки компонентов и панели инструментов данного пакета.

2. Ознакомьтесь с общими требованиями к выполнению схем.

3. Выполните заданный преподавателем чертеж принципиальной элек-

трической схемы в пакете sPlan.

Содержание отчета

1. Цель работы.

2. Распечатка выполненного чертежа.

3. Выводы по работе.

Контрольные вопросы

Для успешной сдачи лабораторной работы студент должен знать от-

веты на представленные ниже вопросы, уметь решать практические задания,

схожие по своей сути с рассмотренными в лабораторной работе, и предста-

вить отчет, выполненный в соответствии с требованиями.

1. Опишите назначение пакета sPlan и его функциональные возможности.

2. Какими достоинствами, на ваш взгляд, обладает программа sPlan?

3. Какие инструменты редактирования чертежей предоставляются паке-

том sPlan?

4. Опишите содержание панели инструментов и панели компонентов дан-

ного графического пакета.

5. Приведите основные требования к выполнению схем согласно стандар-

там ЕСКД.

6. В каком порядке осуществляется нумерация элементов на чертеже

принципиальной электрической схемы?

7. Подробно опишите процесс создания чертежа в sPlan.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Новые информационные технологии : учеб. пособие / под ред. В. П. Дья-

конова. − М. : СОЛОН-Пресс, 2005. – 640 с.

2. Руководство пользователя OpenOffice.org 2. – СПб. : БХВ-Петербург,

2007. – 320 с. : ил + CD-ROM.

3. Советов, Б. Я. Информационные технологии : учеб. для вузов / Б. Я. Со-

ветов, В. В. Цехановский. – 4-е изд., стер. – М. : Высш. шк., 2008. – 263 с.

: ил.

4. Тарнавский, Т. Maxima – максимум свободы символьных вычислений /

Т. Тарнавский // Linux Format. – 2006. – № 7(81).

5. Федосов, Б. Т. Приятное знакомство: «МВТУ» программный комплекс

для моделирования и исследования объектов и систем [Электронный ре-

сурс] / Б. Т. Федосов. – Рудный, 2003.

Интернет-ресурсы

1. http://www.maxima.sourceforge.net/ru/ (17.10.2009)

2. http://www.mvtu.power.bmstu.ru/ (17.10.2009)

3. http://www.ru.openoffice.org/ (17.10.2009)

Учебное издание

Горбунов Алексей Александрович

ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ

Методические указания

Редактор Н. А. Евдокимова

Подписано в печать 20.10.2009. Формат 60

84/16.

Бумага офсетная. Усл. печ. л. 1,63.

Тираж 60 экз. Заказ 1200.

Ульяновский государственный технический университет

432027, г. Ульяновск, ул. Сев. Венец, 32.

Типография УлГТУ, 432027, г. Ульяновск, ул. Сев. Венец, 32.