Goncalves Mario A. Characterization of Geochemical Distributions Using Multifractal Models

Подождите немного. Документ загружается.

P1: Vendor/FNV P2: FLF

Mathematical Geology [mg] PL235-228125 September 29, 2000 11:14 Style ﬁle version June 30, 1999

Mathematical Geology, Vol. 33, No. 1, 2001

Characterization of Geochemical Distributions

Using Multifractal Models

M´ario A. Gon¸calves

The use of multifractals in the applied sciences has proven useful in the characterizationandmodeling

of complex phenomena. Multifractal theory has also been recently applied to the study and charac-

terization of geochemical distributions, and its relation to spatial statistics clearly stated. The present

paper proposesatwo-dimensional multifractal model based on atrinomial multiplicative cascadeas a

proxy to some geochemical distribution. The equations for the generalizeddimensions, mass exponent,

coarse Lipschitz–H

older exponent, and multifractal spectrum are derived. This model was tested with

an example data set used for geochemical exploration of gold deposits in Northwest Portugal. The

element used was arsenic because a large number of sample assays were below detection limit for

gold. Arsenic, however, has a positive correlation with gold, and the two generations of arsenopyrite

identiﬁed in the gold quartz veins are consistent with different mineralizing events, which gave rise to

different gold grades. Performing the multifractal analysis has shown problems arising in the subdivi-

sion of the area with boxes of constant side length and in the uncertainty the edge effects produce in

the experimental estimation of the mass exponent. However, it was possible to closely ﬁt a multifrac-

tal spectrum to the data with enrichment factors in the range 2.4–2.6 and constant K

= 1.3. Such

parameters may give some information on the magnitude of the concentration efﬁciency and hetero-

geneityof the distributionofarsenic in the mineralizedstructures.Ina simple test with estimated points

using ordinary lognormal kriging, the ﬁtted multifractal model showed the magnitude of smoothing

in estimated data. Therefore, it is concluded that multifractal models may be useful in the stochastic

simulation of geochemical distributions.

KEY WORDS: multiplicative cascades, multifractal spectrum, method of moments, enrichment

factor, soil geochemistry, gold exploration.

INTRODUCTION

The notion of multifractals is related to sets that may support self-similar mea-

sures characterized not by a single fractal dimension but a spectrum of such di-

mensions. This notion has been widely applied in physics, to the analysis of tur-

bulence and strange attractors (Feder, 1988), and chemistry (Stanley and Meakin,

Received 23 July 1999; accepted 15 January 2000.

Departamento de Geologia, Faculdade de Ciˆencias da Universidade de Lisboa, Ediﬁcio C2, Piso 5,

Campo Grande, 1749-016 Lisboa, Portugal. e-mail: Mario.Goncalves@fc.ul.pt

0882-8121/01/0100-0041$19.50/1

2001 International Association for Mathematical Geology

P1: Vendor/FNV P2: FLF

Mathematical Geology [mg] PL235-228125 September 29, 2000 11:14 Style ﬁle version June 30, 1999

42 Gon¸calves

1988). Fractals have been also applied in the earth sciences, to tectonics and geo-

chemical distributions (Agterberg and others, 1996; Cheng, 1997; Cheng and

Agterberg, 1995; Cheng and Agterberg, 1996; Cheng, Agterberg, and Ballantyne,

1994; Turcotte, 1997). However, this subject is still regarded sceptically by many

researchers because the concept does not provide a key solution for the physical

understanding of any phenomena it tries to characterize. The fact that multifrac-

tal methods may simulate very complex phenomena does not mean we are able

to understand or draw predictions from them with the fewest possible parame-

ters. Still, the use of fractal models has proved to be in remarkable agreement

with some experimental data of dynamical systems showing chaotic behaviour,

such as turbulent ﬂow (Meneveau and Sreenivasan, 1987). Bearing this in mind,

the goal of this paper is to demonstrate that multifractal models can characterize

complex phenomena in geochemical distributions and improve our knowledge of

them.

Geological phenomena are inherently complex and many features show that

several processes have taken place,overprinting each other andcrafting its present

appearance. This may be viewed as a simple feedback system, in which at least

part of the output of one process becomes the input of the same or of a different

processwithinthegeological sequence of events.Geochemical distributionsareno

exception, and the formation of geochemical anomalies often implies reworking

of former chemically anomalous volumes of rock, enhancing the efﬁciency of the

processes itself, such as the supergene enrichment of ore deposits. This may give

rise to very complex distribution patterns of chemical elements within the crust, or

even on the surface of the Earth. The work of Agterberg (1995), Agterberg, Cheng

andWright(1993),Cheng(1998),ChengandAgterberg(1995),Cheng,Agterberg,

and Ballantyne (1994), and Sim, Agterberg, and Beaudry (1998), for example, use

thetheoryofmultifractalstostudy the spatial distributionofmineralizationphases,

grades of ore deposits, and deﬁnition of anomalies in geochemical distributions.

The model proposed byCheng, Agterberg, and Ballantyne (1994) to separate geo-

chemicalanomaliesfrom background valueshas beenappliedsuccessfullytoother

datasets in thestudy of goldmineralization and vanadium,chromium andnickelin

soils (Gon¸calves,1996; Gon¸calves,Vairinho,and Oliveira, 1998), in which thresh-

old values obtained for each element sometimes had a remarkable agreement with

themean grade in the hostrocks. In some cases this can becorrelated with different

mineralizing events (Gon¸calves, 1996).

This kind of result is quite stimulating and provides the motivation to charac-

terizesuchdistributionsin termsoftheir multifractal spectra f (α)as well. Because

this function contains information about the generating mechanism (Mandelbrot,

1990a), it opens a possible line of research to model natural phenomena. This jus-

tiﬁes the proposal of a multifractal model here, to characterize such distributions.

Theproposed model isby no meansunique, butopens possibilities toexploreother

kinds of similar models.

P1: Vendor/FNV P2: FLF

Mathematical Geology [mg] PL235-228125 September 29, 2000 11:14 Style ﬁle version June 30, 1999

Characterization of Geochemical Distributions Using Multifractal Models 43

MULTIFRACTALS

Multifractalmeasuresarereferredtothestudyofadistributionof a givenphy-

sical quantity on a geometric support (Feder, 1988), or as Evertsz and Mandelbrot

(1992) point out, multifractals is the name by which self-similar measures are

frequently known.

The simplest way to perform multifractal analysis is to partition the measure

and cover it with a set of boxes of ﬁxed size. Let us consider a collection of N

boxes of constant linear size ε, where µ

(ε) is a measure performed in the ith box,

with i = 1,...,N

. This measure is characterized by a scaling exponent α

such

that

(ε) ∼ ε

(1)

where

logµ

(ε)

logε

(2)

is known as the coarse Lipschitz–H

older exponent. It follows that the number of

such boxes N

(α), with a particular value of α, is deﬁned as

(α) ∼ ε

− f

(α)

(3)

If the function f

(α) approaches a limit for ε → 0, then

f (α) =−lim

ε→0

logN

(α)

logε

(4)

This is known as the multifractal spectrum.

The method of moments (Evertsz and Mandelbrot, 1992; Halsey and others,

1986) is a frequently used method to compute the multifractal spectrum, which is

based on the partition function χ

(ε), deﬁned as follows:

(ε) =

i=1

(ε), for q ∈< (5)

If the measure µ

(ε) is exactly self-similar, then χ

(ε) scales with the box size ε

(ε) ∼ ε

τ (q)

(6)

P1: Vendor/FNV P2: FLF

Mathematical Geology [mg] PL235-228125 September 29, 2000 11:14 Style ﬁle version June 30, 1999

44 Gon¸calves

for any order q, where τ (q) is the mass exponent of order q. The mass exponent

τ (q) has a relation with the generalized multifractal dimension D

of the form

(Halsey and others, 1986)

τ (q) = (q − 1)D

(7)

As ε → 0, Equation (5) can be substituted by Equations (1) and (3), yielding

(ε) ∼

αq− f (α)

dα (8)

where only the values that minimize the exponent are the dominant contributors

to the integral. Therefore, according to Equation (6), τ(q) becomes

τ (q) = min

[αq − f (α)] (9)

and the spectrum f (α) is the Legendre transform of τ (q), satisfying the relations

f (α) = qα(q) −τ (q) (10)

∂τ(q)

∂q

=α(q) (11)

and

∂ f (α)

∂α

=q (12)

Mandelbrot (1990a, 1990b) has noted that the multifractal spectrum may

highlight some characteristics not revealed by the approach followed by Halsey

and others (1986), and also that it may give rise to anomalous behavior that reﬂect

the characteristics of some multifractal sets.

A PROPOSED MULTIFRACTAL MODEL

It is widely known that multiplicative processes give rise to continuous mul-

tifractals (e.g., Evertsz and Mandelbrot, 1992; Mandelbrot, 1989), and the ex-

ample of de Wijs (1951) is often used to demonstrate the relation between mul-

tifractals and ore distributions (Cheng and Agterberg, 1996; Mandelbrot, 1989;

P1: Vendor/FNV P2: FLF

Mathematical Geology [mg] PL235-228125 September 29, 2000 11:14 Style ﬁle version June 30, 1999

Characterization of Geochemical Distributions Using Multifractal Models 45

Turcotte, 1997). Therefore, to study the multifractal properties of geochemical

distributions, an artiﬁcial multifractal was constructed based on a trinomial mul-

tiplicative cascade. This model is very much a natural progression of earlier

approaches.

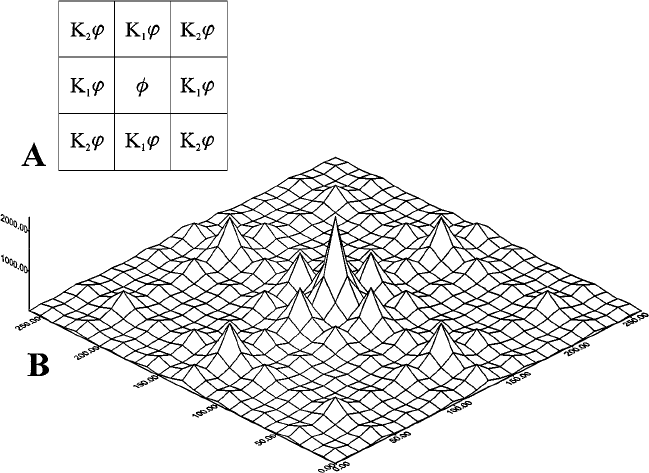
Consider a unit square with unit mass containing a measure of concentration.

In the ﬁrst-order generation (n = 1), the unit square is subdivided into 9 smaller

squares, each of side length ε = 1/3. The initial unit mass is redistributed in such

a way that the central square cell is enriched by a factor φ resulting from a constant

contribution of each of the remaining 8 square cells. Therefore, each of these cells

loses a constant fraction of its mass to the central cell. The remaining mass in

the 8 cells is, however, unevenly distributed such that the 4 cells sharing their

sides with the central cell (hereafter referred as “edge cells”) keep more mass than

the 4 cells at the corners of the initial square (corner cells). In each subsequent

generation, this procedure is repeated for each generated new square cell and its

corresponding mass, as shown in Figure 1A. For any generation of order n, there

are 9

square cells, each with side length ε = 1/3

Figure 1. A, Parent square cell with the subdivisions into 9 cells each of side length ε = 1/3 and their

corresponding multipliers. Eachnew cell isfurther subdivided and its concentration multipliedby each

of the constants as shown (see text for symbol deﬁnitions). B, Surface plot after running the model for

third order cells (n = 3).

P1: Vendor/FNV P2: FLF

Mathematical Geology [mg] PL235-228125 September 29, 2000 11:14 Style ﬁle version June 30, 1999

46 Gon¸calves

According to this model, the enrichment factor φ is such that φ ∈]1,9[, and

theconcentrationmeasuredinacentralcelloforder nisrelatedto theconcentration

of any cell of order n − 1by

1·n

=φC

n−1

(13)

where the index 1 stands for the central cell. The concentration in each of the

4 edge cells is

2·n

= K

ϕC

n−1

(14)

wherethe index2 stands for the edge cell, ϕ is the massfraction left after retrieving

the corresponding fraction to the central cell, and is deﬁned as ϕ = (9 − φ)/8;

∈]1,2[ is a constant. For each of the corner cells, the relation is

3·n

= K

ϕC

n−1

(15)

where the index 3 stands for the corner cell, and K

= 2 − K

. Figure 1B shows

a surface plot for the third generation of this model.

Analyticalexpressionsfor D

,τ (q), α,and f (α) forthemodelcan be derived.

Let the measure of the ith cell be µ

(ε) = C

/nC

, where C

is the concentration in

the ith cell of order n, and C

is the initial concentration. Following the approach of

Turcotte (1997) and using Equation (5), the partition function χ

(ε) for any order

n is given by

(1/3

) =

[4(K

ϕ)

+ 4(K

ϕ)

+ φ

]

(16)

As q → 1, we get a slightly modiﬁed equation (Turcotte, 1997) in order to obtain

an expression for D

, thus χ

(ε) becomes

(1/3

) = 1 + (q − 1)S(1/3

) (17)

with

S(1/3

) =−n

(1 − 1/9φ) ln(1/9K

ϕ) + K

(1 − 1/9φ) ln(1/9K

ϕ)

+ 2/9φ ln(1/9φ)] (18)

P1: Vendor/FNV P2: FLF

Mathematical Geology [mg] PL235-228125 September 29, 2000 11:14 Style ﬁle version June 30, 1999

Characterization of Geochemical Distributions Using Multifractal Models 47

Therefore, using Equation (16) together with Equations (6) and (7), the gen-

eralized dimension D

becomes

=−

(q−1)ln3

·µ

[4(K

ϕ)

+ 4(K

ϕ)

+ φ

]

forq 6= 1 (19)

For q = 1, Equation (17) is used instead, leading to

=−

2ln3

1−

+ K

1 −

φ ln

¶¸

(20)

In Figure 2 the generalized dimension D

is plotted for a range of q values with

different enrichment factors and K

constant. Since this is a two-dimensional

model, D

= 2, which corresponds to the topological dimension of the surface

supporting the measure. As q →∞, with increasing values of φ, the generalized

dimension falls rapidly toward lower values, asymptotically reaching a plateau

closer to 0. Making φ constant, increasing K

raises D

for q < 0, but for q > 0

the generalized dimension takes lowervalues. However, curves with equal φ come

to coincidence for q →∞unless for φ<1.8 the condition φ>9K

(8 + K

)

−1

is not met for some curves.

The above equations can be used to compute the mass exponent τ (q) from

the generalized dimension D

through Equation (7); thus

τ (q) =−

ln3

·µ

[4(K

ϕ)

+ 4(K

ϕ)

+ φ

]

(21)

Using Equation (11), we derive the expression for the coarse Lipschitz–H¨older

exponent,

α(q) =−

ln3

2ln

4(K

ϕ)

ln(K

ϕ) + 4(K

ϕ)

ln(K

ϕ) + φ

lnφ

4(K

ϕ)

+ 4(K

ϕ)

+ φ

(22)

Substituting Equations (21) and (22) into Equation (10) gives the multifractal

spectrum f (α).

Since these expressions have the order parameter q as exponent, there are

numerical limitations in the computation of f (α) for large values of |q|.

The multifractal spectrum can also be computed following the approach of

Evertsz and Mandelbrot (1992) and Mandelbrot (1989).

P1: Vendor/FNV P2: FLF

Mathematical Geology [mg] PL235-228125 September 29, 2000 11:14 Style ﬁle version June 30, 1999

48 Gon¸calves

Figure 2. Plot of the generalized dimension D

in the range −10 ≥ q ≥ 20, for several

enrichment factors φ as indicated beside curves. Dashed and solid lines correspond to the

same enrichment factors but different K

constants (K

= 1.7 and K

= 1.3, respectively).

For the nth-order generation, let s

denote a sequence of v (v = 1, 2, ...,n)

indices i, with i ∈{1,2,3}representing the central cells, edge cells, and corner

cells, such that any concentration may be denoted by C

. Let P

be the frequency

that index i occur in the sequence s

. Therefore, the concentration measured in any

cell of order n is

= φ

(1−P

(23)

Similarly, the number of such cells with an index sequence s

n)!(P

n)!

(1−P

(24)

For n →∞, taking the base 3 logarithm of Equation (24) and expanding it by

using Stirling’s approximation of n! ∼

√

2πn(n/e)

yields

log

∼−

log

− n

log

+ n(1 − P

)log

4 (25)

P1: Vendor/FNV P2: FLF

Mathematical Geology [mg] PL235-228125 September 29, 2000 11:14 Style ﬁle version June 30, 1999

Characterization of Geochemical Distributions Using Multifractal Models 49

Simplifying, Equation (25) becomes

∼ (3

−n

)

−δ(α)

(26)

with

δ(α) ∼−

log

+ (1 − P

)log

4 (27)

The coarse Lipschitz–H¨older exponent is (Evertsz and Mandelbrot, 1992)

α =−

log

(28)

where m

is the corresponding mass fraction in each cell of type i,asgiven

by Equations (13)–(15) assuming a unit concentration. However, the masses of

each of the 9 generated cells must sum up to 1, such that m

+ 4(m

+ m

) = 1,

leading to

, m

, andm

(29)

The plot of Equations (27) and (28) is a domain (α, δ(α)), where the multifractal

spectrum is deﬁned as f (α) = max

[δ(α)].

MODEL PROPERTIES

The multifractal spectrum of the model proposed has some properties that

will be explored brieﬂy to stress how it depends on the distribution of the val-

ues and therefore to gain some a priori insight to what kind of data sets it is

likely best applied. As already mentioned, this model is not unique for charac-

terization of geochemical distributions. To analyze such distributions, we use the

multifractal spectrum f (α), which according to Equation (4) may be viewed as

the logarithm of an expected value. As a result, several situations may arise in

the extremes of the distribution such as in binomial multiplicative cascades where

f (α

min

) = f (α

max

) = 0, a situation never achieved in the model proposed. Other

situations may reveal the existence of negative dimensions [ f (α) < 0], as in some

real data sets (e.g., Chhabra and Sreenivasan, 1991; Mandelbrot, 1990a). The

method of moments, formalized by Halsey and others (1986), often fails to reveal

such characteristic behavior, which led Mandelbrot (1990a) to criticize this ap-

proach strongly. When f (α) = 0, this means that there is a value in the data set

that occurs exactly once per typical sample, and if f (α) < 0 there is a value whose

occurrence is less than once per typical sample. From Equations (23) and (24) it is

P1: Vendor/FNV P2: FLF

Mathematical Geology [mg] PL235-228125 September 29, 2000 11:14 Style ﬁle version June 30, 1999

50 Gon¸calves

obvious that the model proposed does not allow negative dimensions, and there is

only one value that occurs once, corresponding to the cells, for any order n, whose

concentration is C

= φ

. In the other tail of the distribution there are always 4

cells with the minimum possible value of concentration for any order n, implying

that f (α

max

) is always positive.In most situations, f (α

min

) = 0, for q →+∞,but

only for values of φ, such that φ ≥ 1.8orφ>9K

(8 + K

)

−1

. Two other cases

may arise, such that when

φ<1.8∧φ<9K

(8 + K

)

−1

⇒ f (α

min

) = f (α

max

) > 0

and

φ = 9K

(8 + K

)

−1

⇒ f (α

min

) > f (α

max

) > 0

APPLICATION TO GEOCHEMICAL DATA SETS

As mentioned in the introduction, the use of very simple multifractal models

tocharacterizecomplexphenomena(e.g.,Feder,1988;MeneveauandSreenivasan,

1987) can also be used in geochemical exploration. However, problems may arise

suchas the computationof the multifractal spectrum forreal data sets. It mightalso

happen that the proposed model does not describe data sets satisfactorily, an issue

likely to be improved by introducing additional parameters. The major drawback

is that mathematical complexity and handling difﬁculty increase.

In geochemical exploration, the deﬁnition of anomalous threshold values

relative to the background concentration of certain elements of interest is a good

example of how multifractal analysis can be a useful tool. Cheng, Agterberg, and

Ballantyne(1994)haverecentlyproposedamethodnotingthattheareaenclosinga

given concentration shows power law dependence on the concentration and can be

explained assuming the distribution of concentrations is multifractal. Gon¸calves

(1996) and Gon¸calves, Vairinho, and Oliveira (1998) tested this method in two

different situations, both for soil geochemistry, and the results obtained gave a

remarkable agreement with other geological information available. Discrepancies

may be obtained whenever late dispersion mechanisms enter into place. In the

case of gold mineralization (Gon¸calves, 1996), two different levels of gold grade

were found in quartz veins: a low grade ranging from 200 to 500 ppb, and a higher

grade generally from 1000 ppb up to 7000 ppb. The model proposed by Cheng,

Agterberg, and Ballantyne (1994) applied to soil geochemistry in this area gave a

threshold value of 600 ppb for gold, showing agreement with a map of the richest

structures found in the ﬁeld. This data set is the same used in the present study and

was obtained during geochemical exploration for gold deposits in NW of Portugal

(Leduc, 1990).