Головенкин А.Н. Электропривод центробежных механизмов
Подождите немного. Документ загружается.

31
∆Р
р.м.с
=
∆Н
р
·Q, (7.4)
где ∆Н
р
определяется по Q–H характеристикам механизма и магистрали при
механическом способе регулирования производительности (рис.5).
Общий КПД установки при механическом способе регулирования
производительности и нерегулируемом электроприводе определяется как
η
общ.м
= η
д
·η
мех
·η
м.с
, (7.5)
где η
м.с
= ∆Н
р
/Н
р
,
Н
р
– напор на выходе механизма до регулирующего органа.
При механическом способе регулирования производительности вся
реактивная мощность сети (Q
c.м)
потребляется двигателем. Она расходуется на
создание основного магнитного поля двигателя Q
µ
, магнитных полей рассеяния
статорной Q
σ1
и роторной Q
σ2
обмоток. Таким образом, баланс реактивной
мощности в асинхронном двигателе имеет вид
Q
c.м
= Q
д
= Q
µ
+ Q
σ1
+ Q
σ2
. (7.6)
В нерегулируемом электроприводе напряжение и частота питающего
напряжения равны номинальным значениям (U
c
= U
н
, f
c
= f
н
) и составляющие
баланса могут быть определены следующим образом.
Реактивная мощность основного магнитного поля равна
Q
µ
= Q
µ.н
= 3I
2
µ.н
Х
µ.н
, (7.7)
где Х
µ.н
– главное индуктивное сопротивление двигателя при U
c
= U
н
, f
c
= f
н
(каталожные данные);
I
µ.н
– ток намагничивания при U
c
= U
н
, f
c
= f
н
.
Реактивная мощность полей рассеяния обмоток статора и ротора равна
Q
σ1
= 3I
2
1
Х
1н
; Q
σ2
= 3(I
2
'
)
2
Х
2н
'
, (7.8)
где Х
1н
, Х
2н
'
– индуктивное сопротивление рассеяния обмотки статора и
приведенное к статору сопротивление рассеяния обмотки ротора (каталожные
данные);
I
1
, I
2
'
– ток статора и приведенный к статору ток ротора.
Для Г-образной схемы замещения [6] справедливо соотношение I
1
= I
2
'
, в
котором ток ротора I
2
'
может быть найден из уравнения электромагнитной
мощности

32
М·ω
0
= 3 (I
2
'
)
2
R
2
'
/s. (7.9)
Коэффициент мощности асинхронного электродвигателя будет равен
cosφ
дв
=
()
2
.
2
.
.
мcмс
мс
QР
Р
+
. (7.10)
7.2. Электрический способ регулирования производительности
В регулируемом асинхронном электроприводе баланс потребляемой из сети
активной мощности имеет вид
Р
с.э
= ∆Р
д.э
+ Р
пр.с
+ ∆Р
пр.р
+ ∆Р
мех
+ Р
пол
+ Р
рек
, (7.11)
где ∆Р
пр.с
, ∆Р
пр.р
- потери в преобразовательных устройствах соответственно
цепей статора и ротора;
Р
рек
– мощность, рекуперируемая в сеть преобразовательным устройством
роторной цепи, например инвертором в асинхронно-вентильном каскаде;
∆Р
д.э
– потери в пассивных элементах (сопротивлениях) статорной и
роторной цепях двигателя при электрическом способе регулирования
производительности.
Здесь потери в сопротивлениях статорной и роторной цепях двигателя
представляются в виде
переменных и постоянных (независящих от нагрузки)
потерь.
Методика расчета потерь зависит от способа регулирования скорости.
При параметрическом, реостатном и частотном
регулировании переменные потери
в пассивных элементах статорной и
роторной цепях двигателя могут быть выражены через электромагнитный момент
и абсолютное скольжение:
∆Р
д.э.пер
= М·(ω
0
-ω)(1+ R
1∑
/ R
/
2∑
), (7.12)
где R
1∑
, R
/
2∑
– сопротивление цепи статора и приведенное сопротивление
цепи ротора;
ω
0
– синхронная скорость двигателя при номинальной частоте питающего
напряжения.
При параметрическом способе регулирования скорости изменением
величины питающего напряжения и использовании асинхронного двигателя с

33
фазным ротором в суммарное сопротивление цепи ротора в уравнении (7.12)
входит и добавочное сопротивление
R
/
2∑
= R
/
2
+ R
/
доб
.
При
реостатном способе регулирования верно соотношение
R
/
2
/ R
/
2∑
= (ω
0
-ω
н
)/(ω
0
-ω),
и выражение для переменных потерь (7.12) преобразуется к виду
∆Р
д.э.пер.р
= М·(ω
0
-ω) + М·(ω
0
-ω
н
) R
1
/ R
/
2
, (7.13)
где первое слагаемое определяет потери в роторной цепи, второе – в статоре.
При
частотном регулировании абсолютное скольжение определяется как
ω
0
– ω = (ω
0
– ω
макс
)·М/М
смакс
,
и формула для расчета переменных потерь приобретает вид
∆Р
д.э.пер.ч
= М
2
(ω
0
-ω
макс
)(1+ R
1∑
/ R
/
2
) / М
смакс
. (7.14)
В формуле (7.14) учтено отсутствие добавочных сопротивлений в роторной цепи
при частотном регулировании.
При графическом методе определения переменных потерь в уравнения
(7.12) – (7.14) подставляются координаты (М
СТ
,ω
Т
) текущей точки механической
характеристики нагрузки М
С
= f(ω) в заданном диапазоне изменения скорости.
При аналитическом методе расчета используются уравнения
аппроксимации характеристики нагрузки (6.8) и (6.9), и расчетные формулы
приобретают следующий вид.
При
параметрическом регулировании:
∆Р
д.э.пер.п
= М
смакс
к
макс
ω
ω
·(ω
0
-ω)(1+ R
1∑
/ R
/
2∑
). (7.15)
Максимальные потери имеют место при скорости ω
м
= к ω
0
/(к+1) и равны
∆Р
д.э.пер.п.м
=
.1
)1(
/
2
1
1
0
1
+⋅
+
⋅
Σ
Σ
+
+
R
R
к
к
М
к
к
к
к
макс
смакс
ω
ω
(7.16)
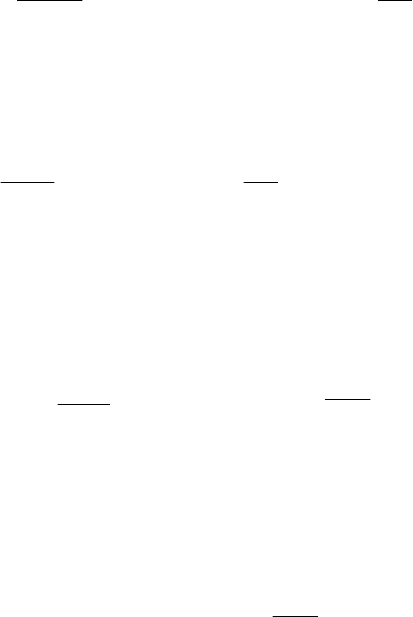
34
При
реостатном регулировании зависимость потерь от скорости имеет
вид
∆Р
д.э.пер.р
= М
смакс .)()(
/
2
1
00
макс
⋅−+−
R
R
н
к
ωωωω
ω
ω
·(7.17)
Максимальные потери могут быть определены по формуле (7.17) при скорости
−+
+
=
/
2
1
00
)(
1
R
R
к
к
нм
ωωωω
. (7.18)
При
частотном способе регулирования переменные потери определяются
как
∆Р
д.э.пер.ч
= М
смакс
к2
макс
ω
ω
(ω
0
- ω
макс
)· (1+
/
2
1
R
R
Σ
). (7.19)
Максимальные потери определяются по формуле (7.19) для максимальной
скорости ω
макс
из заданного диапазона изменения скорости:
∆Р
пер.ч.м
= М
смакс
(ω
0
- ω
макс
)·(1+
/
2
1
R
R
Σ
). (7.20)
К
постоянным потерям асинхронного двигателя относят механические
потери ∆Р
п.мех
, потери в стали статора ∆Р
п.с.с.
и ротора ∆Р
п.с.р
, а также потери в
меди статора от намагничивающего тока I
µ
, т.е.
∆Р
пост
= ∆Р
п.мех
+ ∆Р
п.с.с
+ ∆Р
п.с.р
+ 3I
µ
2
·R
1
. (7.21)
Для механических потерь можно принять
∆Р
п.мех
= ∆Р
п.мех.н
(ω/ω
н
)
n
, (7.22)
где ∆Р
п.мех.н
– механические потери при номинальной скорости двигателя;
n = 1 – 1,3.
Номинальные механические потери зависят от номинальной мощности и для
мощностей Р
н
= 20 – 100 кВт могут быть оценены как
∆Р
п.мех.н
= к
м
Р
н
, где к
м
= 0,01-0,015. (7.23)
35
В выражении (7.23) большие значения коэффициента к
м
относятся к большим
номинальным скоростям и меньшим мощностям двигателей.
Потери в стали (от вихревых токов и гистерезиса) пропорциональны
квадрату напряжения и частоте в степени примерно 1,3. Поскольку объемы
шихтованной стали статора и ротора равны, суммарные потери здесь можно
определить как
∆Р
п.с
= ∆Р
п.с.с
+ ∆Р
п.с.р
= ∆Р
п.с.с.н
(U/U
н
)
2
·(ƒ/ƒ
н
)
1,3
(1 + s
1,3
), (7.24)
где ∆Р
п.с.с.н
– потери в стали статора при номинальных частоте ƒ
н
и напряжении
питания U
н
.
Расчет постоянных
потерь при параметрическом, реостатном и частотном
способах регулирования различен.
При
реостатном способе регулирования U = U
н
, ƒ = ƒ
н
. При этом
∆Р
п.с
= ∆Р
п.с.с.н
(1 + s
1,3
), (7.25)
т.е. суммарные потери в стали при снижении скорости растут за счет роста
потерь в стали ротора. Пренебрегая номинальными потерями в роторе, а также
считая, что увеличение потерь в стали ротора компенсируется в диапазоне
скоростей от номинальной до нуля снижением механических потерь, можно
считать постоянные потери при реостатном способе регулирования не
зависящими от скорости и равными номинальным потерям, определенным при
номинальной скорости:
∆Р
пост.р
= ∆Р
пост.н
= ∆Р
п.мех.н
+ ∆Р
п.с.с.н
+ 3I
µ.н
2
·R
1
, (7.26)
где I
µ.н
– ток намагничивания при номинальном напряжении U
н
.
При
параметрическом способе регулирования скорости изменением
напряжения на статоре двигателя составляющие потерь в стали и в меди статора
от намагничивающего тока не являются постоянными. Принимая допущение о
взаимной компенсации потерь в стали ротора и механических потерь, а также
имея в виду уравнение (7.24) и пренебрегая номинальными потерями в стали
ротора, можно считать что постоянные потери при параметрическом способе
равны
∆Р
пост.п
= ∆Р
п.мех.н
+ [∆Р
п.с.с.н
+ 3I
µ.н
2
·R
1
](U/U
н
)
2
. (7.27)
При
частотном регулировании рабочее скольжение двигателя остается
небольшим на всем диапазоне изменения скорости, поэтому потерями в стали

36
ротора (также как при параметрическом способе) можно пренебречь. Тогда для
случая регулирования по закону U/f = const, согласно выражению (7.24), получим
∆Р
п.с
= ∆Р
п.с.с.н
3,3
3,12
3,3
2
⋅∆=
⋅
н
пссн
нн
f
f
Р
fU
f
f
U
, (7.28)
по закону f = var
∆Р
п.с
= ∆Р
п.с.с.н
(f/f
н
).
Суммарные постоянные потери при частотном способе регулирования будут
равны при U/f = const:
∆Р
пост.ч
= ∆Р
п.мех.н
(ω/ω
н
)
n
+ ∆Р
п.с.с.н
·
3,3
н
f
f
+ 3I
µ.н
2
·R
1
, (7.29)
при f = var:
∆Р
пост.ч
= ∆Р
п.мех.н
(ω/ω
н
)
n
+ ∆Р
п.с.с.н
·
3,1
н
f
f
+ 3I
µ.н
2
·R
1
(f
н
/f)
2
.
Методика расчета постоянных потерь асинхронного двигателя следующая.
1. Определяются номинальные потери через номинальные КПД (η
н
) и
мощность(Р
н
) двигателя как
∆Р
дн
=
Н
Н
P
η
- P
н
. (7.30)
2. Находятся номинальные переменные потери по формуле
∆Р
дер.н
= М
н
ω
0
s
н
(1+ R
1∑
/ R
/
2∑
).
3. Номинальные постоянные потери (при номинальной скорости) будут
равны
∆Р
дост.н
= ∆Р
дн
- ∆Р
дер.н
.
4. Постоянные потери в зависимости от способа регулирования находятся
по формулам (7.22), (7.23) и (7.25). Необходимые составляющие постоянных
потерь определяются с учетом выражения (7.18) и уравнения баланса
номинальных постоянных потерь:
∆Р
п.с.с.н
= ∆Р
пост.н
- ∆Р
п.мех.н
- ∆Р
п.с.с.н
- 3I
µ.н
2
·R
1
. (7.31)
37
Потери в преобразовательных устройствах цепей статора Р
пр.с
(частотное и
параметрическое управление) можно определить с помощью КПД и выходной
мощности преобразователя:
Р
пр.с
= Р
п
(1/η
п
-1),
где Р
п
, η
п
– выходная мощность преобразователя и соответствующий этой
мощности КПД.
В каскадных схемах регулирования переменные потери следует
выражать через параметры цепи выпрямленного напряжения роторной цепи. При
соединении обмоток статора и ротора в звезду переменные потери в двигателе и
преобразовательных устройствах будут равны
∆Р
пр.пер
+∆Р
д.э.пер.к
= 2I
2
d
( R
2
+ R
/
1
+ R
пр.р
) + ∑∆U
B
·I
d
, (7.32)
где R
2
– активное сопротивление фазы ротора асинхронного двигателя;
R
/
1
– приведенное к цепи ротора активное сопротивление фазы статора;
R
пр.р
– активное сопротивление преобразовательных устройств цепи ротора;
∑∆U
B
- падение напряжения на вентилях цепи ротора при прохождении
прямого тока.
Для вентильно-машинного каскада с машиной постоянного тока в
роторной цепи сопротивление преобразовательных устройств равно
R
пр.р
= R
пр.р.вм
= R
сд
+ R
я.мп
,
где R
сд
– сопротивление сглаживающего дросселя;
R
я.мп
– сопротивление якоря машины постоянного тока (МП).
Средний выпрямленный ток I
d
может быть найден из решения уравнений
электрического равновесия роторной цепи и баланса моментов на валу каскада в
установившемся режиме:
E
do
s = E
мп
+ I
d
·R
э
, (7.33)
М = E
do
·I
d
/ ω
0
+ кФ
мп
·I
d
, (7.34)
где R
э
= mx
дв
s / 2π + 2R
2
+ 2R
/
1
s+ R
сд
+ R
я.мп
– эквивалентное сопротивление;
m – число фаз выпрямителя (для трехфазной мостовой схемы m = 6 );
x
дв
= x
'
1
+ x
2
– приведенное к ротору сопротивление рассеяния фазы
двигателя;
E
do
– среднее напряжение на выходе выпрямительного моста при
разомкнутой цепи постоянного тока и скольжении s = 1;
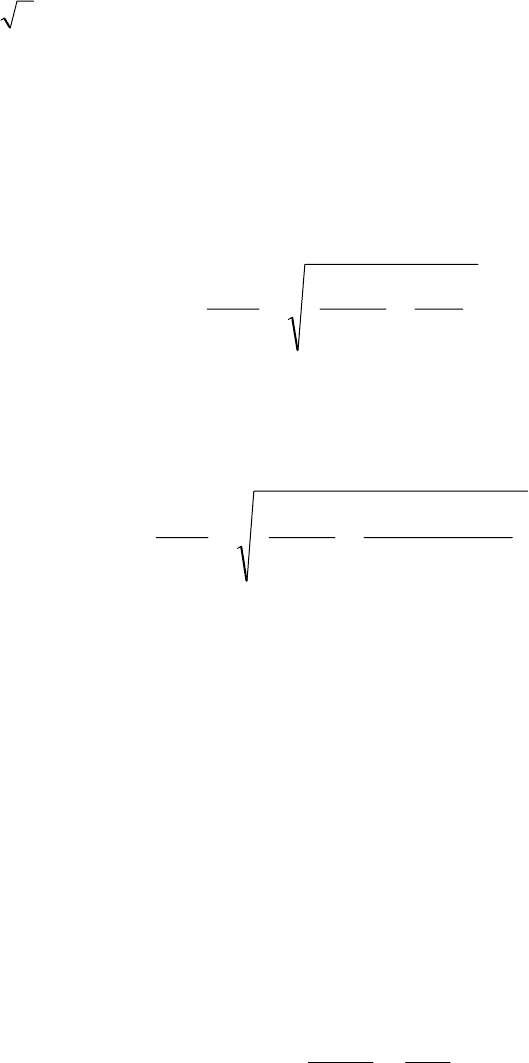
38
E
do
=
2
E
2к
·m/π·sin π/m (при m = 6 E
do
= 1,35 E
2к
) ;
E
мп
= к Ф
мп
ω – э.д.с. двигателя постоянного тока;
к,Ф
мп
– конструктивный коэффициент и магнитный поток МП.
В уравнениях (7.33) и (7.34) не учтено падение напряжения на вентилях ∑∆U
B
и
на сопротивлениях рассеяния двигателя x
дв
.
Совместное решение уравнений (7.33) и (7.34) дает
−−=
Э
Э
do
Э
do
d
R
М
R
Е
R
Е
I
ω
2
2
4
2
. (7.35)
Используя уравнения аналитической аппроксимации характеристики нагрузки
(6.7) и (6.8), получим
⋅
⋅
−−=
+
к
максЭ
к
макс
Э
do
Э
do
d
R
М
R
Е
R
Е
I
ω
ω
1
2
2
4
2
.
(7.36)
В
асинхронно-вентильном каскаде сопротивление
преобразовательных устройств состоит из сопротивлений обмоток
трансформатора (R
тр
) и сглаживающего дросселя (R
сд
):
R
пр.р
= R
пр.р.ав
= R
тр
+ R
сд
.
Средний выпрямленный ток I
d
может быть найден как
I
d
= М·ω
0
/Е
do
. (7.37)
Аналитическое выражение для среднего тока I
d
имеет вид
I
d
= М
смакс
do
к
Е
0
макс
ω
ω
ω
. (7.38)
Зависимость ∆Р
д.э.пер.к
= f(ω) строится по уравнениям (7.32), (7.35), (7.37) с
использованием характеристики нагрузки М
С
= f(ω) или по уравнениям (7.32),
(7.36) и (7.38).
Постоянные потери в асинхронном двигателе в каскадных схемах
увеличиваются за счет наличия высших гармоник в токе статора и ротора
приблизительно на 5% в сравнении с обычной схемой включения. Постоянные
потери в естественной схеме включения асинхронного двигателя

39
∆Р
пост.н
= Р
н
(1 – η
н
)/ η
н
- М
н
ω
0
s
н
(1+ R
1∑
/ R
/
2∑
). (7.39)
Постоянные потери в каскаде
∆Р
пост.к
= 1,05 ∆Р
пост.н
+ ∆Р
пост.пр
, (7.40)
где ∆Р
пост.пр
– постоянные потери в преобразовательных устройствах роторной
цепи.
В вентильно-машинном каскаде постоянные потери в
преобразовательных устройствах равны постоянным потерям машины
постоянного тока. С некоторым приближением можно считать, что снижение
потерь в цепи обмотки возбуждения машины постоянного тока МП при
увеличении скорости компенсируется увеличением механических потерь и потерь
в стали. Поэтому постоянные потери в преобразовательных устройствах роторной
цепи при регулировании скорости остаются постоянными и равны потерям
холостого хода машины постоянного тока:
∆Р
пост.пр
= Р
н.мп
(1 – η
н.мп
)/ η
н.мп
– I
2
н.мп
R
я.мп
, (7.41)
где Р
н.мп
, I
н.мп
,η
н.мп
– номинальные мощность, ток и КПД машины постоянного
тока.
В асинхронно-вентильном каскаде
∆Р
пост.пр
= ∆Р
х.х.тр
,
где ∆Р
х.х.тр
- потери холостого хода трансформатора инвертора (даны в
паспортных данных).
Потери в исполнительном механизме и полезная мощность (Р
пол
и ∆Р
мех
)
при электрическом способе регулирования производительности определяются по
формулам (7.1) и (7.3).
Коэффициент полезного действия электрических способов регулирования
производительности определяется как отношение полезной мощности на выходе
магистрали к потребляемой мощности из сети:
η
общ.р
= Р
пол
/Р
с
. (7.42)
Баланс
реактивных мощностей для регулируемого электропривода имеет
вид
Q
c.э
= Q
д
+ Q
пр.с
+ Q
пр.р
, (7.43)

40
где Q
c.э
– реактивная мощность, потребляемая из сети;
Q
д
, Q
пр.с
, Q
пр.р
– реактивные мощности, потребляемые соответственно
двигателем, преобразовательными устройствами статорной и роторной цепей.
Составляющие баланса реактивной мощности (7.43) зависят от способа
регулирования скорости при электрическом способе регулирования
производительности.
При
реостатном регулировании напряжение и частота тока статора
асинхронного двигателя так же, как и при механическом способе, постоянны, и
реактивная мощность двигателя может быть определена по формулам
(7.6 – 7.9), в которых вместо R
2
'
следует подставить R
2
'
+ R
доб
.
Для асинхронных двигателей с фазным ротором в справочных данных, как
правило, дан ток ротора при номинальной нагрузке. В этом случае, используя
соотношение
М = кФ
н
I
2
'
cosφ
2
, (7.44)
где
cosφ
2
=
2
2
2
2
2
/
X
s
R
sR
′
+
′
′
;
кФ
н
= М
н
/ I
2н
'
cosφ
2н
,
можно найти текущее значение I
2
'
= f(М) для определения реактивных потерь
рассеяния.
При реостатном способе Q
пр.с
и Q
пр.р
следует принять равными нулю.
При
параметрическом регулировании изменением напряжения на
статоре реактивная мощность двигателя также может быть определена по
формулам (7.6),(7.8) и (7.9). Однако мощность основного потока будет равна
Q
µ
= Q
µ.н.
( U/U
н
)
2
. (7.45)
Тиристорные коммутаторы, магнитные усилители, используемые для
регулирования напряжения статора, повышают потребление реактивной
мощности на 7 - 10%.
При
частотном регулировании и использовании для расчета формул
(7.6),(7.8) и (7.9) следует иметь в виду зависимость составляющих баланса
реактивной мощности от напряжения и частоты:
Q
µ
= Q
µ.н.
( U/U
н
)
2
(f
н
/f), (7.46)
Q
σ1
= 3I
2
1
Х
1н
(f/f
н
), (7.47)
