Голдаев С.В. Практикум по математическому моделированию в теплоэнергетике
Подождите немного. Документ загружается.


ɆɂɇɂɋɌȿɊɋɌȼɈ ɈȻɊȺɁɈȼȺɇɂə ɂ ɇȺɍɄɂ ɊɈɋɋɂɃɋɄɈɃ ɎȿȾȿɊȺɐɂɂ
Ƚɨɫɭɞɚɪɫɬɜɟɧɧɨɟ ɨɛɪɚɡɨɜɚɬɟɥɶɧɨɟ ɭɱɪɟɠɞɟɧɢɟ ɜɵɫɲɟɝɨ ɩɪɨɮɟɫɫɢɨɧɚɥɶɧɨɝɨ ɨɛɪɚɡɨɜɚɧɢɹ
«ɇȺɐɂɈɇȺɅɖɇɕɃ ɂɋɋɅȿȾɈȼȺɌȿɅɖɋɄɂɃ
ɌɈɆɋɄɂɃ ɉɈɅɂɌȿɏɇɂɑȿɋɄɂɃ ɍɇɂȼȿɊɋɂɌȿɌ»
ɋ.ȼ. Ƚɨɥɞɚɟɜ
ɉɊȺɄɌɂɄɍɆ
ɉɈ ɆȺɌȿɆȺɌɂɑȿɋɄɈɆɍ
ɆɈȾȿɅɂɊɈȼȺɇɂɘ
ȼ ɌȿɉɅɈɗɇȿɊȽȿɌɂɄȿ
Ɋɟɤɨɦɟɧɞɨɜɚɧɨ ɜ ɤɚɱɟɫɬɜɟ ɭɱɟɛɧɨɝɨ ɩɨɫɨɛɢɹ
Ɋɟɞɚɤɰɢɨɧɧɨ-ɢɡɞɚɬɟɥɶɫɤɢɦ ɫɨɜɟɬɨɦ
Ɍɨɦɫɤɨɝɨ ɩɨɥɢɬɟɯɧɢɱɟɫɤɨɝɨ ɭɧɢɜɟɪɫɢɬɟɬɚ
ɂɡɞɚɬɟɥɶɫɬɜɨ
Ɍɨɦɫɤɨɝɨ ɩɨɥɢɬɟɯɧɢɱɟɫɤɨɝɨ ɭɧɢɜɟɪɫɢɬɟɬɚ
2011
ɍȾɄ 536.24
ȻȻɄ 22.19
Ƚ60
Ƚɨɥɞɚɟɜ ɋ.ȼ.
Ƚ60 ɉɪɚɤɬɢɤɭɦ ɩɨ ɦɚɬɟɦɚɬɢɱɟɫɤɨɦɭ ɦɨɞɟɥɢɪɨɜɚɧɢɸ ɜ ɬɟɩɥɨ-
ɷɧɟɪɝɟɬɢɤɟ: ɭɱɟɛɧɨɟ ɩɨɫɨɛɢɟ / ɋ.ȼ. Ƚɨɥɞɚɟɜ; Ɍɨɦɫɤɢɣ ɩɨɥɢɬɟɯ-
ɧɢɱɟɫɤɢɣ ɭɧɢɜɟɪɫɢɬɟɬ. – Ɍɨɦɫɤ: ɂɡɞ-ɜɨ Ɍɨɦɫɤɨɝɨ ɩɨɥɢɬɟɯɧɢ-
ɱɟɫɤɨɝɨ ɭɧɢɜɟɪɫɢɬɟɬɚ, 2011. – 152 ɫ.
ȼ ɩɨɫɨɛɢɢ ɪɚɫɫɦɨɬɪɟɧɵ ɩɪɢɦɟɪɵ ɢɡ ɩɪɨɦɵɲɥɟɧɧɨɣ ɬɟɩɥɨɷɧɟɪɝɟ-
ɬɢɤɢ, ɫɜɹɡɚɧɧɵɟ ɫ ɚɜɬɨɦɚɬɢɡɚɰɢɟɣ ɪɚɫɱɟɬɨɜ ɢ ɦɚɬɟɦɚɬɢɱɟɫɤɢɦ ɦɨɞɟɥɢɪɨ-
ɜɚɧɢɟɦ ɩɪɨɰɟɫɫɨɜ. ɉɪɨɜɟɞɟɧɢɟ ɷɬɢɯ ɨɩɟɪɚɰɢɣ ɨɫɭɳɟɫɬɜɥɟɧɨ ɫ ɩɪɢɦɟɧɟ-
ɧɢɟɦ ɨɫɧɨɜɧɵɯ ɱɢɫɥɟɧɧɵɯ ɦɟɬɨɞɨɜ, ɪɟɚɥɢɡɨɜɚɧɧɵɯ ɧɚ ɩɟɪɫɨɧɚɥɶɧɨɦ
ɤɨɦɩɶɸɬɟɪɟ ɜ ɜɢɞɟ ɩɪɨɝɪɚɦɦ ɜ ɫɪɟɞɟ «Ɍɭɪɛɨ-ɉɚɫɤɚɥɶ».
ɉɪɟɞɧɚɡɧɚɱɟɧɨ ɞɥɹ ɩɨɞɝɨɬɨɜɤɢ ɦɚɝɢɫɬɪɨɜ ɩɨ ɧɚɩɪɚɜɥɟɧɢɸ 140100
«Ɍɟɩɥɨɷɧɟɪɝɟɬɢɤɚ»
ɍȾɄ 536.24
ȻȻɄ 22.19
Ɋɟɰɟɧɡɟɧɬɵ
Ʉɚɧɞɢɞɚɬ ɬɟɯɧɢɱɟɫɤɢɯ ɧɚɭɤ
ɞɢɪɟɤɬɨɪ ɋɩɟɰɢɚɥɢɡɢɪɨɜɚɧɧɨɣ ɷɤɫɩɟɪɬɧɨɣ ɧɚɭɱɧɨ-
ɢɫɫɥɟɞɨɜɚɬɟɥɶɫɤɨɣ ɢ ɧɚɥɚɞɨɱɧɨɣ ɨɪɝɚɧɢɡɚɰɢɢ
ɈɈɈ «ɂɧɠɟɧɟɪɧɵɣ ɰɟɧɬɪ «Ɍɟɩɥɨɭɧɢɜɟɪɫɚɥ»
Ȼ.ȼ. Ʌɟɛɟɞɟɜ
Ʉɚɧɞɢɞɚɬ ɬɟɯɧɢɱɟɫɤɢɯ ɧɚɭɤ, ɞɨɰɟɧɬ ɌɍɋɍɊɚ
ɇ.ɉ. Ɇɢɧɶɤɨɜɚ
© ȽɈɍ ȼɉɈ ɇɂ Ɍɉɍ, 2011
© Ƚɨɥɞɚɟɜ ɋ.ȼ., 2011
© Ɉɛɥɨɠɤɚ. ɂɡɞɚɬɟɥɶɫɬɜɨ Ɍɨɦɫɤɨɝɨ
ɩɨɥɢɬɟɯɧɢɱɟɫɤɨɝɨ ɭɧɢɜɟɪɫɢɬɟɬɚ, 2011
3
Предисловие
При оценке и расчетах различных типов энергетических и
технологических систем, на стадии так называемого поискового
конструирования с выбором наиболее эффективного варианта,
требуется всесторонняя оценка теплообменных процессов, знание
формирующихся в агрегатах температурных полей, определения всех
необходимых энергетических характеристик с учетом
эксплуатационных нагрузок.
Математическое моделирование теплоэнергетических систем как
метод исследования в настоящее
время получил широкое
распространение. Математическая модель в отличие от реально
поставленного эксперимента имеет следующие преимущества: 1)
экономия материальных ресурсов, требуемых для постановки и
проведения физического эксперимента; 2) возможность апробации
системы в экстремальных условиях и даже за их пределами; 3) оценка
работоспособности систем с длительными технологическими циклами
(недели, месяцы, годы) в существенно более сжатые
сроки.
Математическое моделирование может проводиться и в процессе
эксплуатации оборудования при проведении его мониторинга,
оптимизации технологического режима, при создании и внедрении в
производство различных схем его автоматизированного управления.
При исследовании сложных систем используются два
взаимосвязанных направления: 1) изучение процессов в элементах
установок; 2) изучение установок как систем взаимосвязанных
элементов.
Анализ процессов
теплоэнергетических систем, химической
технологии показывает, что они могут рассматриваться как
совокупность элементарных процессов, каждый из которых вносит
определенный вклад в скорость суммарного процесса. Элементарный
процесс удается достаточно точно описать на основе законов тепло-
массобмена, механики жидкости и газа, свести к известной краевой
задаче, воспользоваться точным или приближенным ее решением. Это
представляет один из перспективных путей исследования
промышленного процесса.
Однако использование теоретических методов затруднено
недостаточной изученностью сложных взаимодействующих процессов
в теплоэнергетических системах. Возможности экспериментальных
исследований ограничены, поскольку они могут реализоваться только
на действующих установках, в то время как часто необходимо строить
математическую модель новых, еще не существующих аппаратов, в
4
которых реализованы другие принципы интенсификации тепло-
массообмена, новые материалы и т. п.
Практические методики расчета характеристик теплообменных
аппаратов, газо-и паротурбинных установок, компрессоров,
экономайзеров, воздухоподогревателей и т. п. представляют собой
громоздкие выражения, в которых необходимо использовать
табличные значения свойств рабочих тел, привлекать номограммы.
При «ручных» вычислениях основное время тратится
на поиск этих
данных и запись промежуточных вычислений. В усовершенствованных
методиках нередко используются основные численные методы:
решение систем линейных и трансцендентных уравнений, вычисление
определенных интегралов, интегрирование систем обыкновенных
дифференциальных уравнений, решение краевых задач, описываемых
одномерным и двухмерным уравнением теплопроводности.
Поэтому магистранты должны владеть приемами автоматизации
подобных расчетов, которые основаны на
использовании известных
интерполяционных зависимостей для физических величин,
температурных напоров или получении для них аппроксимационных
выражений.
В пособии дано описание двадцати лабораторных работ,
представляющих примеры задач из промышленной теплоэнергетики.
Задания расположены в таком порядке, что позволяют
последовательно осваивать упомянутые методы и элементы
программирования: использование меток, безусловных и условных
циклов, функций и
процедур, массивов (одномерных и двухмерных),
отладочной печати и др. Программы написаны просто, чтобы
пользователь, изучавший ранее программирование и освоивший
основные конструкции среды «Турбо Паскаль», мог выполнять
параметрический анализ установки, а при необходимости –
модифицировать программу. Для экономии места порой не соблюдены
требования читаемости программы (выделение начала и конца блока,
использование нескольких
операторов на одной строке и т. п.). Эти
недостатки могут быть преодолены на самих занятиях, где не
возникает такой необходимости.
5
1. Расчет характеристик двигателей внутреннего сгорания
Двигатель внутреннего сгорания (ДВС) – тепловая машина,
в которой подвод теплоты к рабочему телу осуществляется за счет сжи-
гания жидкого и газообразного топлива внутри самого двигателя. Они
входят в конструкции автомобилей, кораблей и самолетов.
Поршневой ДВС, по сравнению с любым другим тепловым двига-
телем, является
экономичным. Ему присуща быстрота запуска, малая
металлоемкость и относительная долговечность. Стационарные двига-
тели применяются на электростанциях для привода насосных установок,
на нефте- и газоперекачивающих и буровых установках, в сельском хо-
зяйстве и т. п. Передвижные двигатели устанавливаются на автомоби-
лях, тракторах, самолетах, судах, локомотивах. ДВС незаменимы в лес-
промхозах, геолого
-разведочных партиях и т. п. Кроме того, они рабо-
тают на металлургических заводах, используя в качестве топлива до-
менный газ и генераторный газ.
Мощность существующих стационарных двигателей составляет от
20 до 3500 кВт, а общая мощность поршневых двигателей в настоящее
время значительно превышает мощность всех электростанций.
Все современные ДВС разделяются
на три группы: 1) с быстрым
сгоранием топлива при постоянном объеме (ДВС Отто); 2) с постепен-
ным сгоранием топлива при постоянном давлении (ДВС Дизеля); 3) со
смешанным сгоранием топлива частично при постоянном объеме и час-
тично при постоянном давлении (ДВС Тринклера).
В поршневых ДВС рабочим телом является смесь воздуха и паров
жидкого топлива (
на начальном участке цикла) и продукты сгорания на
остальных участках цикла.
Степень сжатия (ε) в двигателе Отто ограничивается температурой
самовоспламенения горючей смеси. При некоторых значениях ε, часто
происходит воспламенение горючей смеси, а затем ее детонация. В ре-
зультате процесс сгорания нарушается, мощность двигателя падает, рас-
ход топлива возрастает. Значение ε
зависит от качества топлива и повы-
шается с улучшением антидетонационных свойств, характеризуемых ок-
тановым числом.
Для повышения ε в цикле Дизеля применяют сжатие не горючей
смеси, а чистого воздуха. Жидкое топливо вводится в цилиндр в конце
процесса сжатия. Раздельное сжатие воздуха и жидкого топлива исклю-
чает самовоспламенение и позволяет получать
степени сжатия ε =
14…18. Давление в конце сжатия может достигать 3…4 МПа, а темпе-
ратура – 600…800
о
С.
6
Значение ε в двигателе Дизеля должно обеспечить самовоспламе-
нение топлива и создать температурные условия для быстрого протека-
ния процесса сгорания.
Недостатками двигателя Дизеля, по сравнению с двигателем Отто,
являются: наличие компрессора для распыления жидкого топлива, на
работу которого расходуется 6…10 % общей мощности двигателя;
сложные устройства насоса и форсунки; относительная тихоходность,
обусловленная медленным сгоранием топлива.
Цель работы
На основе автоматизированной методики осуществить расчет ос-
новных характеристик ДВС, работающего по циклу Тринклера.
Принцип работы ДВС, со смешанным подводом теплоты
Русский инженер Г. В. Тринклер построил бескомпрессорный дви-
гатель высокого давления, работающий со смешанным подводом тепло-
ты (рис. 1.1) частично при v
= const, а частично – при p = const.
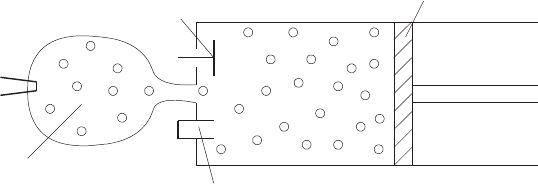
Рис. 1.1. Схема ДВС, работающего по циклу Тринклера
Жидкое топливо подается к форсункам насосом при давлении
30…40 МПа. Распыление жидкого топлива производится при помощи
механических форсунок и происходит в предкамере, которая установ-
лена в верхней части цилиндра и соединена с рабочим объемом цилинд-
ра одним или несколькими узкими каналами. Сжатие воздуха осущест-
вляется так же, как в компрессорных двигателях
, до температур, обес-
печивающих самовоспламенение топлива.
Жидкое топливо поступает в предкамеру через форсунку, форма и
расположение которой способствуют хорошему смешению жидкого то-
плива с воздухом. Процесс смешения в предкамере протекает следую-
щим образом. В процессе сжатия давление в цилиндре растет быстрее,
чем в предкамере. За счет разности давлений возникает
поток воздуха
из цилиндра в предкамеру, который используется для распыления жид-
Всасывающий клапан
Выхлопной клапан
Форсунка
Поршень
Предкамера
7
кого топлива, впрыскивается в предкамеру. При этом образуется одно-
родная смесь, сгорающая в предкамере при постоянном объеме. Давле-
ние в предкамере возрастает, и направление потока изменяется: смесь
продуктов сгорания и несгоревших паров топлива, имеющих темпера-
туру 1500…1800
о
С, устремляется из предкамеры в цилиндр, где проис-
ходит перемешивание и догорание. В результате поршень перемещается
слева направо при постоянном давлении. После сгорания топлива про-
исходит адиабатное расширение продуктов сгорания. Затем они удаля-
ются из цилиндра.
Методика расчета
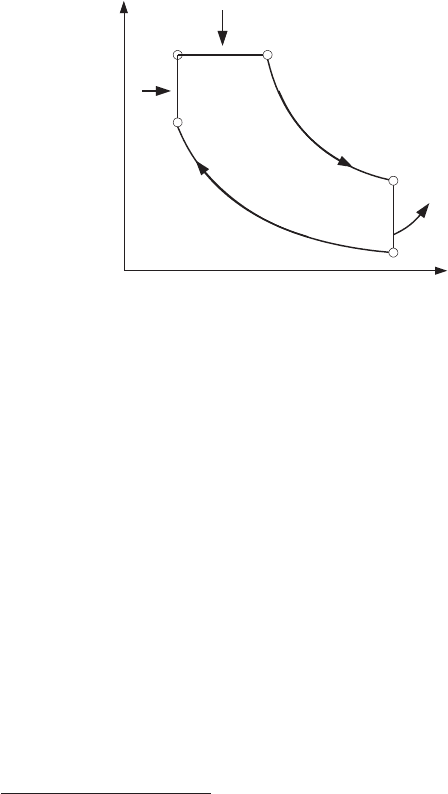
Термодинамический цикл Тринклера состоит (рис. 1.2) из следую-
щих процессов: 1–2 –
адиабатное сжатие воздуха; подвод теплоты: 2–3 –
изохорный, 3–4 – изобарный; 4–5 – адиабатное расширение продуктов
сгорания; 5–1 – изохорный отвод теплоты.
1
v
p
2
3
4
q
2
q
1
q
1
5
адиабата
адиабата
Рис. 1.2. Pv-диаграмма цикла Тринклера
Параметрами, характеризующими цикл со смешанным подводом
теплоты, являются степени: ε = v
1
/v
2
– адиабатного сжатия; λ = p
3
/p
2
–
повышения давления; ρ = v
4
/v
3
=
v
4
/v
2
– предварительного (изобарного)
расширения; δ = v
5
/v
4
– адиабатного расширения.
Теплота, отводимая по изохоре 5–1, определяется соотношением:
152
TTcq
v
. (1.1)
Подведенная теплота равна сумме теплот, подведенных в изохор-
ном (2–3) и в изобарном (3–4) процессах:
34231
TTcTTcq
pv
. (1.2)
Подставляя значения q
1
и q
2
в выражение для термического КПД,
получаем после элементарных преобразований
>@
3423
15
1
TTkTT
TT
k
tvp
. (1.3)
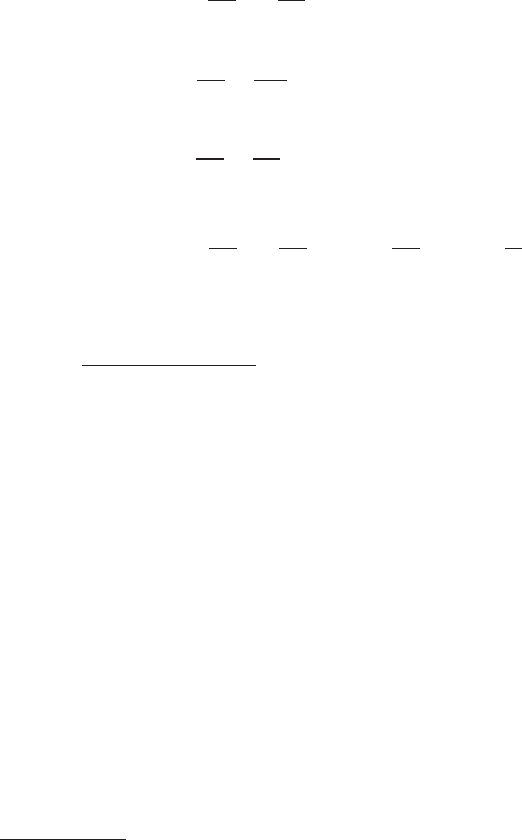
8
Выразим температуры T
2
, T
3
, T
4
и T
5
через T
1
и параметры цикла:
для адиабаты 1–2:
1
1
2
1
1
2
ε
¸
¸
¹
·
¨
¨
©
§
k
k
v
v
T
T
. (1.4)
для изохоры 2–3:
1
13
2
3
2
3
ελλ;
k
TT
p
p
T
T
. (1.5)
для изобары 3–4:
1
14
3
4
3
4
ερλρ;
k
TT
v
v
T
T
. (1.6)
для адиабаты 4–5:
1
1
1
4
1
5
4
4
5
ε
ρ
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
k
k
k
v
v
v
v
T
T
. (1.7)
Подставляя выражения (2.4)–(2.7) в (2.3), получаем:
>@
1ρλ1λ
1λρε
1
1
k
k
kk
tvp
. (1.8)
При λ = 1 цикл Тринклера обращается в цикл Отто, а при ρ = 1 – в цикл
Дизеля.
Из выражения (1.8) следует, что термический КПД цикла Тринкле-
ра возрастает с увеличением ε, k и λ. С увеличением ρ термический КПД
уменьшается. Для таких двигателей обычно принимают: ε = 10…14, λ =
1,2…1,7 и ρ = 1,1…1,5.
Работа цикла
определяется выражением
>@
^`
1ρλ1ρλ1λε
1
121
kk
vc
kTcqql
. (1.9)
Среднее индикаторное давление цикла (среднее цикловое давле-
ние), представляющее собой работу цикла, приходящуюся на единицу
рабочего объема цилиндра двигателя, в цикле Тринклера определяется
таким образом:
>@
kk
c
k
k
p
p
11
1
ε1δ1ρλ11ρλ
11ε
. (1.10)
Пример 1. Для ДВС, работающему по циклу Тринклера (рис. 1.2),
известны параметры: p
1
= 0,1 МПа; t
1
= 0
о
C; p
4
= 7,0 МПа; p
5
= 0,35 МПа;
теплота, подведенная в изохорном процессе, q
z23
= 234 кДж/кг.
Определить: неизвестные термодинамические параметры в точках,
подведенную теплоту q
1
, отведенную теплоту q
2
, работу цикла l
c
, сред-
нее индикаторное давление p
c
,
термический
КПД k
tvp
.
Опишем алгоритм решения примера.
Для точки 1 по уравнению состояния идеального газа
111
/ pTRv
b
.
Для точки 5 по условию изохорности процесса
15
vv
, а темпера-
тура
b
RvpT /
555
. Для точки 4 из уравнения адиабаты находим
9
kk
ppTT
/1
5454
/
,
444
/ pTRv
b
. Предполагаем, что давление в точке 2
равно, например, 5,0 МПа. Тогда из уравнения адиабаты находим тем-
пературу
kk
ppTT
/1
1212
/
, удельный объем
222
/ pTRv
b
. По условию
изохорности
23
vv
, а из условия изобарности
43
pp
. Температура в
точке 3 равна
b
RvpT /
333
. Подведенную теплоту на участке 2–3 вы-
числяем по формуле
2323
TTcq
v
, где
)1/( kRc
bv
– удельная мас-
совая теплоемкость при постоянном объеме. Находим относительную
погрешность определения q
23
. Если расхождение превышает заданное
значение, то давление в точке 2 изменяется. Процедура продолжается до
тех пор, пока эта погрешность не станет приемлемой. По формуле (1.1)
находится q
2
, а по формуле (1.2) – q
1
. Затем вычисляется работа и тер-
мический КПД цикла. Для проверки правильности найденных значений
термодинамических параметров в точках и характеристик цикла вычис-
ляются параметры цикла Тринклера
δλ,ρ,ε,
и по формулам (1.8) –
(1.10) подсчитываются: термический КПД, l
c
и p
c
.
Отсюда видно, что расчет даже одного варианта представляет собой
трудоемкую процедуру, поэтому целесообразно воспользоваться ПК.
Листинг 1. Расчет термодинамических параметров ДВС, рабо-
тающего по циклу Тринклера
Program CikL_TrincLera;
Uses Crt;
Const Rb=287.0; k=1.4; Tk0=273; pm=1.0e5; kj=1e3; eqz=0.01;
Var cv, cp, tс1, Tk1, v1, p1, Tk2, v2, p2, Tk3, v3, p3, T4, v4, p4, Tk5,
v5, p5, Lc, pc, ktpv, ev, Lm, r0, de, q1, q2, k1, qz23, q23, eq, F0, Fe, Fk, FL,
Fd, Fp:real;
Begin ClrScr;
p1:=1.0e5; tс1:=0; p4:=70e5; p5:=3.5e5; qz23:=234.0;
k1:=(k–1)/k; cv:=Rb/(k–1); cp:=k*cv;
Tk1:=tс1+tk0; v1:=Rb*Tk1/p1;
v5:=v1; Tk5:=p5*v5/Rb;
Writeln('p1=',p1/pm:4:1,' v1=',v1:4:3,' Tk1=',Tk1:4:1,
'p5=',p5/pm:4:1,' v5=',v5:4:3,' Tk5=',Tk5:4:1);
Tk4:=Tk5*exp(k1*ln(p4/p5)); v4:=Rb*Tk4/p4;
Writeln('p4=',p4/pm:4:1,' v4=',v4:4:3,' Tk4=',Tk4:4:1);
p2:=40e5;
Repeat
p2:=p2+0.1e5;
Tk2:=Tk1*exp(k1*ln(p2/p1));
10
v2:=Rb*Tk2/p2; v3:=v2; p3:=p4;
Tk3:=p3*v3/Rb; p3:=p3/pm;
q23:=cv*(Tk3–Tk2)/kj;
eq:=abs((q23–qz23)/qz23);
Until eq<eqz;
Writeln('p2=',p2/pm:4:1,' v2=',v2:4:3,' Tk2=',Tk2:4:1,' p3=',p3:4:1,
'v3=',v3:4:3,'Tk3=',Tk3:4:1,' q23=',q23:4:1,' eq=',eq:4:3);
q2:=cv*(Tk5–Tk1)/kj;
q1:= q23+cp*(Tk4–Tk3)/kj;
Lc:=q1–q2; ktpv:=1–q2/q1; e
v:=v1/v2; de:=v5/v4; r0:=v4/v2; Lm:=p3/p2;
Writeln('q1=',q1:4:1,' q2=',q2:4:1,' Lc=',Lc:4:1,' ktpv=',ktpv:4:3);
Writeln('ev=',ev:4:3,'r0=',r0:4:3,'de=',de:4:1,'
Lm=',Lm:4:2,'eq=',eq:4:3);
F0:= Lm*exp(k*ln(r0))–1;
Fe:= exp((k–1)*ln(ev));
FL:= (Lm–1+k*Lm*(r0–1))*Fe–F0;
Fk:=(Lm–1+k*Lm*(r0–1))*Fe;
Fd:=exp((1–k)*ln(de));
Fp:= Lm*((r0–1)*(k–1)+r0*(1–Fd))–1+1/Fe;
Lc:=cv*T1*FL/kj; ktpv:=1–F0/Fk;
pc:=(p1/pm)*Fp/((ev–1)*(k–1));
Writeln('Lc=',Lc:4:1,' ktpv=',ktpv:4:3,' pc=',pc:4:2); end.
Файл результатов решения примера 1:
p
1
= 1.0; v
1
= 0.784; T
k1
= 273.0; p
5
= 3.5; v
5
= 0.784; T
k5
= 955.5;
p
4
= 70.0; v
4
= 0.092; T
k4
= 2248.8; p
2
= 50.3; v
2
= 0.048; T
k2
= 836.2;
p
3
= 70.0; v
3
= 0.048; T
k3
= 1163.7; q
23
= 235.0; e
q
= 0.004;
q
1
= 1324.9; q
2
= 489.7; L
c
= 835.3; k
tpv
= 0.630;
e
v
= 16.4; r
0
= 1.932; d
e
= 8.5; L
m
= 1.39;
L
c
= 835.3; k
tpv
= 0.630; p
c
= 0.23.
Параметрический анализ показывает, что при одинаковых ε и q
1
термический КПД цикла Тринклера больше КПД цикла Отто, но мень-
ше КПД цикла Дизеля.
При одинаковых конечных давлениях и температурах T
3
= T
max
во
всех трех циклах и одинаковом значением q
2
– КПД цикла Тринклера
больше КПД цикла Отто, но меньше КПД цикла Дизеля.
При этих условиях наибольшая степень сжатия будет у двигателей
с подводом теплоты при p = const.
