Gibilisco S. Teach Yourself Electricity and Electronics

Подождите немного. Документ загружается.

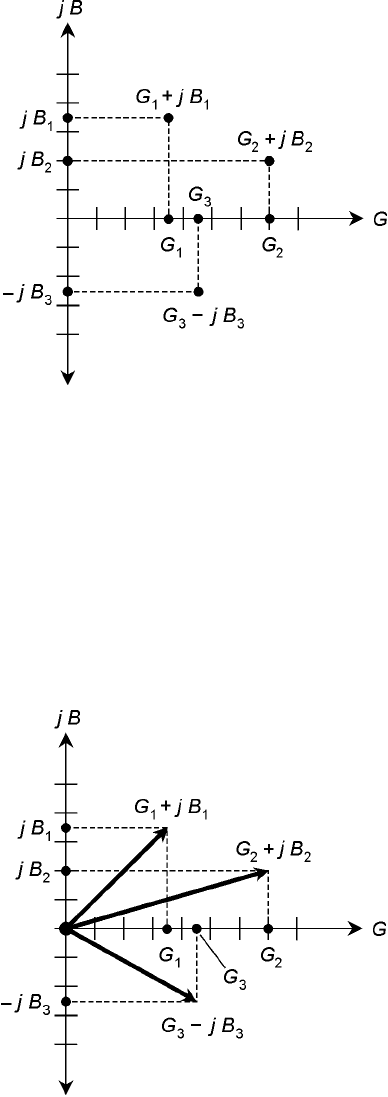
Vector Representation of Admittance

Complex admittances can be shown as vectors, just as can complex impedances. In Fig. 15-10, the

points from Fig. 15-9 are rendered as vectors.

Generally, long vectors in the GB plane indicate large currents, and short vectors indicate

small currents. Imagine a point moving around on the GB plane, and think of the vector getting

longer and shorter and changing direction. Vectors pointing generally northeast, or upward and to

the right, correspond to conductances and capacitances in parallel. Vectors pointing in a more or

less southeasterly direction, or downward and to the right, are conductances and inductances in

parallel.

The GB Plane 241

15-10 Vectors representing

the points of

Fig. 15-9.

15-9 Some points in the

complex admittance

plane, and their

conductive and

susceptive components

on the axes.

Quiz

Refer to the text in this chapter if necessary. A good score is 18 or more correct. Answers are in the

back of the book.

1. The square of an imaginary number

(a) can never be negative.

(b) can never be positive.

(d) is equal to j.

2. A complex number

(a) is the same thing as an imaginary number.

(b) has a real-number part and an imaginary-number part.

(d) is a concept reserved for elite mathematicians.

3. What is the sum of 3 + j 7 and −3 − j 7?

(a) 0 + j0

(b) 6 + j14

(d) 0 − j14

4. What is (−5 + j 7) − (4 − j5)?

(a) −1 + j2

(b) −9 − j2

(d) −9 + j12

5. What is the product (−4 − j 7)(6 − j2)?

(a) 24 − j14

(b) −38 − j34

(d) −24 + j14

6. What is the magnitude of the vector 18 − j24?

(a) 6

(b) 21

(d) 52

7. The complex impedance value 5 + j0 represents

(a) a pure resistance.

(b) a pure inductance.

242 Impedance and Admittance

(d) an inductance combined with a capacitance.

8. The complex impedance value 0 − j22 represents

(a) a pure resistance.

(b) a pure inductance.

(d) an inductance combined with a resistance.

9. What is the absolute-value impedance of 3.0 − j 6.0?

(a) Z = 9.0 Ω

(b) Z = 3.0 Ω

(d) Z = 6.7 Ω

10. What is the absolute-value impedance of 50 − j235?

(a) Z = 240 Ω

(b) Z = 58,000 Ω

(d) Z =−185 Ω

11. If the center conductor of a coaxial cable is made to have a smaller diameter, all other things

being equal, what will happen to the Z

of the transmission line?

(a) It will increase.

(b) It will decrease.

(d) There is no way to determine this without knowing the actual dimensions.

12. If a device is said to have an impedance of Z = 100 Ω, you can reasonably expect that this

indicates

(a) R + jX = 100 + j0.

(b) R + jX = 0 + j100.

(d) the reactance and the resistance add up to 100 Ω.

13. Suppose a capacitor has a value of 0.050 µF at 665 kHz. What is the capacitive susceptance,

stated as an imaginary number?

(a) B

= j4.79

(b) B

=−j4.79

= j0.209

(d) B

=−j 0.209

Quiz 243

14. An inductor has a value of 44 mH at 60 Hz. What is the inductive susceptance, stated as an

imaginary number?

(a) B

=−j0.060

(b) B

= j0.060

=−j17

(d) B

= j17

15. Susceptance and conductance add to form

(a) complex impedance.

(b) complex inductance.

(d) complex admittance.

16. Absolute-value impedance is equal to the square root of which of the following?

(a) G

+ B

(b) R

+ X

(d) Y

+ R

17. Inductive susceptance is defined in

(a) imaginary ohms.

(b) imaginary henrys.

(d) imaginary siemens.

18. Capacitive susceptance values can be defined by

(a) positive real numbers.

(b) negative real numbers.

(d) negative imaginary numbers.

19. Which of the following is false?

(a) B

= 1/X

(b) Complex impedance can be depicted as a vector.

(d) G = 1/R.

20. In general, as the absolute value of the impedance in a circuit increases,

(a) the flow of ac increases.

(b) the flow of ac decreases.

(d) the resistance decreases.

244 Impedance and Admittance

WHEN YOU SEE AN AC CIRCUIT THAT CONTAINS COILS AND/OR CAPACITORS, YOU SHOULD ENVISION a

complex-number plane, either RX (resistance-reactance) or GB (conductance-admittance). The RX

plane applies to series circuit analysis. The GB plane applies to parallel circuit analysis.

Complex Impedances in Series

When you see resistors, coils, and capacitors in series, each component has an impedance that can

be represented as a vector in the RX plane. The vectors for resistors are constant, regardless of the

frequency. But the vectors for coils and capacitors vary with frequency.

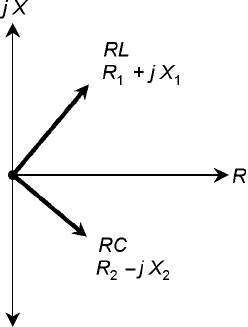
Pure Reactances

Pure inductive reactances (X

) and capacitive reactances (X

) simply add together when coils and

capacitors are in series. Thus, X = X

+ X

. In the RX plane, their vectors add, but because these vec-

tors point in exactly opposite directions—inductive reactance upward and capacitive reactance

downward (Fig. 16-1)—the resultant sum vector inevitably points either straight up or straight

down, unless the reactances are equal and opposite, in which case they cancel and the result is the

zero vector.

Problem 16-1

Suppose a coil and capacitor are connected in series, with jX

= j200 and jX

=−j150. What is the

net reactance?

Just add the values: jX = jX

+ jX

= j200 + (−j150) = j(200 − 150) = j50. This is a pure induc-

tive reactance, because it is positive imaginary.

Problem 16-2

Suppose a coil and capacitor are connected in series, with jX

= j30 and jX

=−j110. What is the

net reactance?

245

CHAPTER

RLC and GLC

Circuit Analysis

Again, add the values: jX = j30 + (−j110) = j(30 − 110) =−j80. This is a pure capacitive reac-

tance, because it is negative imaginary.

Problem 16-3

Suppose a coil of inductance L = 5.00 µH and a capacitor of capacitance C = 200 pF are connected

in series. Suppose the frequency is f = 4.00 MHz. What is the net reactance?

First, calculate the reactance of the inductor at 4.00 MHz. Proceed as follows:

= j6.28fL

= j(6.28 × 4.00 × 5.00)

= j126

Next, calculate the reactance of the capacitor at 4.00 MHz. Proceed as follows:

=−j[1/(6.28fC)]

=−j[1/(6.28 × 4.00 × 0.000200)]

=−j199

Finally, add the inductive and capacitive reactances to obtain the net reactance:

jX = jX

+ jX

= j126 + (−j199)

=−j 73

This is a pure capacitive reactance.

Problem 16-4

What is the net reactance of the aforementioned inductor and capacitor combination at the fre-

quency f = 10.0 MHz?

246 RLC and GLC Circuit Analysis

16-1 Pure inductance and

pure capacitance

are represented by

reactance vectors that

point straight up and

down.

First, calculate the reactance of the inductor at 10.0 MHz. Proceed as follows:

= j6.28fL

= j(6.28 × 10.0 × 5.00)

= j314

Next, calculate the reactance of the capacitor at 10.00 MHz. Proceed as follows:

=−j[1/(6.28fC)]

=−j[1/(6.28 × 10.0 × 0.000200)]

=−j 79.6

Finally, add the inductive and capacitive reactances to obtain the net reactance:

jX = jX

+ jX

= j314 + (−j79.6)

= j234

This is a pure inductive reactance. For series-connected components, the condition in which the

capacitive and inductive reactances cancel is known as series resonance. We’ll deal with this in more

detail in the next chapter.

Adding Impedance Vectors

In the real world, there is resistance, as well as reactance, in an ac series circuit containing a coil and

capacitor. This occurs because the coil wire has some resistance (it’s never a perfect conductor). It

can also be the case because a resistor is deliberately connected into the circuit.

Whenever the resistance in a series circuit is significant, the impedance vectors no longer point

straight up and straight down. Instead, they run off toward the northeast (for the inductive part of

the circuit) and southeast (for the capacitive part). This is illustrated in Fig. 16-2.

Complex Impedances in Series 247

16-2 When resistance is

present along with

reactance, impedance

vectors point at

angles; they are

neither vertical nor

horizontal.

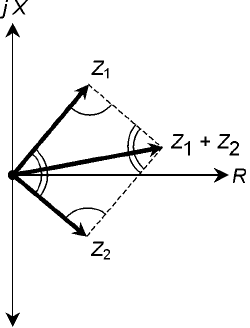
When two impedance vectors don’t lie along a single line, you must use vector addition to be

sure that you get the correct net impedance. In Fig. 16-3, the geometry of vector addition is shown.

Construct a parallelogram, using the two vectors Z

= R

+ jX

and Z

= R

+ jX

as two adjacent sides

of the figure. The diagonal of the parallelogram is the vector representing the net complex imped-

ance. (Note that in a parallelogram, pairs of opposite angles have equal measures. These equalities

are indicated by single and double arcs in Fig. 16-3.)

Formula for Complex Impedances in Series

Suppose you are given two complex impedances, Z

= R

+ jX

and Z

= R

+ jX

. The net imped-

ance, Z, of these in series is their vector sum, given by the following formula:

Z = (R

+ jX

) + (R

+ jX

)

= (R

+ R

) + j(X

+ X

)

Calculating a vector sum using the formula is easier than doing it geometrically with a parallelo-

gram. The arithmetic method is also more exact. The resistance and reactance components add sep-

arately. Just remember that if a reactance is capacitive, then it is negative imaginary in this formula.

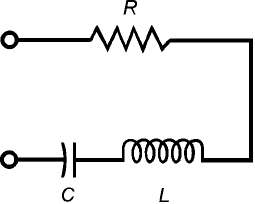
Series RLC Circuits

When an inductance, capacitance, and resistance are connected in series (Fig. 16-4), the resistance

R can be imagined as belonging entirely to the coil, when you use the preceding formulas. Then you

have two vectors to add, when finding the impedance of the series RLC circuit containing three such

components:

Z = (R + jX

) + (0 + jX

)

= R + j(X

+ X

)

Again, remember that X

is never positive! So, although the formulas here have addition symbols in

them, you’re adding a negative number when you add in a capacitive reactance.

248 RLC and GLC Circuit Analysis

16-3 Parallelogram method

of complex-impedance

vector addition.

Problem 16-5

Suppose a resistor, a coil, and a capacitor are connected in series with R = 50 Ω, X

= 22 Ω, and

=−33 Ω. What is the net impedance, Z?

Consider the resistor to be part of the coil, obtaining two complex vectors, 50 + j 22 and 0 −

j33. Adding these gives the resistance component of 50 + 0 = 50, and the reactive component of

j22 − j33 =−j11. Therefore, Z = 50 − j11.

Problem 16-6

Consider a resistor, a coil, and a capacitor that are connected in series with R = 600 Ω, X

= 444 Ω,

and X

=−444 Ω. What is the net impedance, Z?

Again, imagine the resistor to be part of the inductor. Then the complex impedance vectors are

600 + j444 and 0 − j444. Adding these, the resistance component is 600 + 0 = 600, and the reac-

tive component is j444 − j444 = j0. Thus, Z = 600 + j0. This is a purely resistive impedance, and

you can rightly call it 600 Ω.

Problem 16-7

Suppose a resistor, a coil, and a capacitor are connected in series. The resistor has a value of 330 Ω,

the capacitance is 220 pF, and the inductance is 100 µH. The frequency is 7.15 MHz. What is the

complex impedance of this series RLC circuit at this frequency?

First, calculate the inductive reactance. Remember that X

= 6.28fL and that megahertz and

microhenrys go together in the formula. Multiply to obtain the following:

= j(6.28 × 7.15 × 100)

= j4490

Next, calculate the capacitive reactance using the formula X

=−1/(6.28fC). Convert 220 pF to mi-

crofarads to obtain C = 0.000220 µF. Then calculate:

=−j[1/(6.28 × 7.15 × 0.000220)]

=−j101

Now, lump the resistance and the inductive reactance together, so one of the impedance vectors

is 330 + j4490. The other is 0 − j101. Adding these gives Z = 330 + j4389; this rounds off to

Z = 330 + j4390.

Series RLC Circuits 249

16-4 A series resistance-

inductance-capacitance

(RLC) circuit.

Problem 16-8

Suppose a resistor, a coil, and a capacitor are connected in series. The resistance is 50.0 Ω, the in-

ductance is 10.0 µH, and the capacitance is 1000 pF. The frequency is 1592 kHz. What is the com-

plex impedance of this series RLC circuit at this frequency?

First, calculate X

= 6.28fL. Convert the frequency to megahertz; 1592 kHz = 1.592 MHz.

Then:

= j(6.28 × 1.592 × 10.0)

= j100

Then calculate X

=−1/(6.28fC). Let’s convert picofarads to microfarads, and use megahertz for

the frequency. Therefore:

=−j[1/(6.28 × 1.592 × 0.001000)]

=−j100

Let the resistance and inductive reactance go together as one vector, 50.0 + j100. Let the capacitive

reactance be represented as 0 − j100. The sum is Z = 50.0 + j100 − j100 = 50.0 + j0. This is a pure

resistance of 50.0 Ω. You can correctly say that the impedance is 50.0 Ω in this case.

Complex Admittances in Parallel

When you see resistors, coils, and capacitors in parallel, remember that each component, whether it

is a resistor, an inductor, or a capacitor, has an admittance that can be represented as a vector in the

GB plane. The vectors for pure conductances are constant, even as the frequency changes. But the

vectors for the coils and capacitors vary with frequency.

Pure Susceptances

Pure inductive susceptances (B

) and capacitive susceptances (B

) add together when coils and ca-

pacitors are in parallel. Thus, B = B

+ B

. Remember that B

is never positive, and B

is never neg-

ative. This is just the opposite situation from reactances.

In the GB plane, pure jB

and jB

vectors add. Because such vectors always point in exactly op-

posite directions—inductive susceptance down and capacitive susceptance up—the sum, jB, in-

evitably points either straight down or straight up (Fig. 16-5), unless the susceptances are equal and

opposite, in which case they cancel and the result is the zero vector.

Problem 16-9

Suppose a coil and capacitor are connected in parallel, with jB

=−j0.05 and jB

= j0.08. What is

the net susceptance?

Just add the values as follows: jB = jB

+ jB

=−j0.05 + j0.08 = j0.03. This is a capacitive sus-

ceptance, because it is positive imaginary.

Problem 16-10

Suppose a coil and capacitor are connected in parallel, with jB

=−j0.60 and jB

= j0.25. What is

the net susceptance?

250 RLC and GLC Circuit Analysis