Гельруд Я.Д. Линейное программирование. Учебно-методический комплекс
Подождите немного. Документ загружается.


49
а) Рассмотрим отношения чисел, стоящих в правых частях (3.2.1), к
соответствующим коэффициентам при новой базисной переменной x
j
(не
обращая внимание на отношения, в которых знаменатель равен нулю или
представляет собой отрицательное число).
б) Выберем отношение с наименьшим значением — в очередном пробном
решении x
j
приравнивается именно этому значению. Пусть наименьшее из
всех отношений правых частей (3.2.1) к соответствующим коэффициентам
при x
j
соответствует переменной x
k
, входившей в предыдущее решение; тогда
в очередном пробном решении следует положить x
k
= 0. Результаты
вычислений приведены в табл. 3.1.
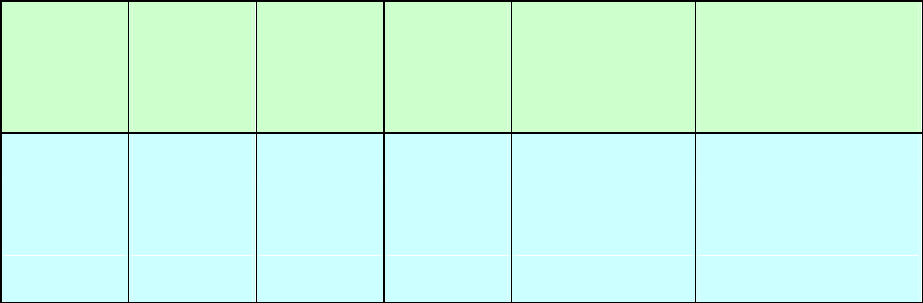
Таблица 3.1
Итерация 1: включение x
4
в очередной базис (согл. критерию II)
Базисные
перемен-
ные
Рассматриваемое
пробное решение
Коэффи-
циенты
при x
4
Значения
отношений
Мини-
мальное
значение
Следующее
пробное
решение
x
0
0 –11
x
5
15 1 15
x
6
120 2 60
x
7
100 15 6,66 6,66 x
4
=6,66, x
7
=0
Теперь, когда известно, что в пробном базисе x
7
следует заменить на x
4
,
перейдем к шагу 4. Перепишем соотношения (3.2.1) таким образом, чтобы в
строке 3 коэффициент при x
4
был равен единице, а в строках 0, 1 и 2 – нулю.
Процедуру, с помощью которой это достигается, называют операцией замены
базиса или операцией замены опорного плана. Сначала разделим обе части
уравнения в строке 3 на коэффициент при x
4
, т. е. на 15:
1x
0
–4x
1
– 5x
2
– 9x
3
– 11x
4
=0 (строка 0),
1x
1
+ 1x
2
+ 1x
3
+ 1x
4
+1x
5
=15 (строка 1), (3.2.2)
7x
1
+ 5x
2
+ 3x
3
+ 2x
4
+1 x
6
= 120 (строка 2),
5
1
x
1
+
3
1
x
2
+
3
2
x
3
+1x
4
+
15
1
x
7
=
3
20
(строка 3).

50
В результате коэффициент при x
4
в строке 3 принял значение, равное
единице. Обратим в нули коэффициенты при x
4
в строках 0, 1 и 2, действуя по
следующей схеме:
1) умножить строку 3 на 11 и результат прибавить к строке 0;
2) умножить строку 3 на –1 и результат прибавить к строке 1;
3) умножить строку 3 на –2 и результат прибавить к строке 2.
Выполнив указанные выше действия, получим
1x
0
–
5
9
x
1
–
3
4
x
2
–
3
5
x
3
+
15
11
x
7
=
3
220
(строка 0),
5
4
x
1
+
3
2
x
2
+
3
1
x
3
+1x
5
–
15
1
x
7
=
3
25
(строка 1), (3.2.3)
5
33
x
1
+
3
13
x
2
+
3
5
x
3
+1x
6
–
15
2
x
7
=
3
320
(строка 2),
5
1
x
1
+
3
1
x
2
+
3
2
x
3
+1x
4
+
15
1
x
7
=
3
20
(строка 3).
Несмотря на то, что система уравнений (3.2.3) выглядит иначе, нежели си-
стема (3.2.1), можно утверждать, что они эквивалентны. Удобство
представления системы уравнений в виде (3.2.3) состоит в том, что, полагая
x
1
= x
2
= x
3
= x
7
= 0, можно сразу же определить значения переменных для
нового пробного базисного решения: x
0
=
3
220
, x
5
=
3
25
, x
6
=
3
320
, x
4
=
3
20
.
Для нового базиса прибыль x
0
равняется 220/3; при этом численное
значение прибыли для рассматриваемого пробного решения определяется по
следующей формуле:
Прибыль для нового пробного решения = Прибыль при предыдущем
пробном базисе + Значение новой базисной переменной × Удельный вклад
новой базисной переменной в приращение прибыли (см. строку 0 в системе
уравнений (3.2.2)):
3
220
= 0+
3
20
⋅11.
Смысл критерия II становится теперь более ясным. Если бы вместо x
7
из
первоначального базиса мы исключили x
5
(или x
6
), то x
4
, x
7
и x
6
(или x
5
)
51
приняли бы отрицательные значения, что противоречит предположению о
том, что ни одна из переменных не может быть отрицательной. Данное
утверждение легко проверить с помощью простых вычислений.
Итерация 2. Завершив первую итерацию, следует вернуться к шагу 2, с
тем, чтобы определить, является ли полученное решение оптимальным. Если
оптимум еще не достигнут, необходимо в
соответствии с симплексным
алгоритмом приступить к следующей итерации.
Согласно критерию I, возможность улучшить решение действительно
существует. При этом в очередной базис выгодно включить либо x
1
, либо x
2
,
либо x
3
. На основании критерия I выбор падает на x
1
, так как эта переменная
обеспечивает наибольшее удельное приращение для значения целевой
функции. Сделав данный выбор, следует перейти к вычислениям,
предусмотренным шагом 3, используя при этом критерий II (табл. 3.2).
Таблица 3.2
Итерация 2: включение x
1
в очередной базис (согл. критерию II)
Базисные
перемен-
ные
Рассмат-
риваемое
пробное
Коэффи-
циенты
при x
1
Значения
отноше-
ний
Минимальное
значение
Следующее
пробное решение
x
0
220/3 9/5
x
5
25/3 4/5 125/12 125/12 x
1
=125/12, x
5
=0
x
6
320/3 33/5 1600/99
x
4
20/3 1/5 100/3
В соответствии с табл. 3.2 в очередном пробном решении x
5
следует
заменить на x
1
. Теперь с учетом произведенной замены нужно
соответствующим образом преобразовать систему уравнений (3.2.3).
Вычислительную процедуру, позволяющую поменять пробный базис (см. шаг
4), можно реализовать в несколько приемов. Вначале выполним нормировку
коэффициента при x
1
в строке 1:

52
1x
0
–
5
9
x
1
–
3
4
x
2
–
3
5
x
3
+
15
11
x
7
=
3
220
(строка 0),
1x
1
+
6
5
x
2
+
12
5
x
3
+
4
5
x
5
–
12
1
x
7
=
12
125
(строка 1), (3.2.4)
5
33
x
1
+
3
13
x
2
+
3
5
x
3
+1x
6
–
15
2
x
7
=
3
320
(строка 2),
5
1
x
1
+
3
1
x
2
+
3
2
x
3
+1x
4
+
15
1
x
7
=
3
20
(строка 3).
Затем, завершая операцию поиска очередного опорного плана, исключим x
1
из уравнений в строках 0, 1 и 3, действуя по следующей схеме:
1) умножить строку 1 на 9/5 и результат сложить со строкой 0;
2) умножить строку 1 на –33/5 и результат сложить со строкой 2;
3) умножить строку 1 на –1/5 и результат сложить со строкой 3.
В результате получим
1x
0
+
6
1
x
1
–
12
11
x
2
+
4
9
x
5
+
12
7
x
7
=
12
1105
(строка 0),
1x
1
+
6
5
x
2
+
12
5
x
3
+
4
5
x
5
–
12
1
x
7
=
12
125
(строка 1), (3.2.5)
–
6
7
x
2
–
12
13
x
3
–
4
33
x
5
+1x
6
+
12
5
x
7
=
12
455
(строка 2),
6
1
x
2
+
12
7
x
3
+1x
4
–
4
1
x
5
+
12
1
x
7
=
12
55
(строка 3).
Третье пробное базисное решение следующее: x
0
=
12
1105
, x
1
=
12
125
, x
6
=
12
455
,
x
4
=
12
55
. Заметим, что на каждой итерации коэффициент при переменной, не
вошедшей в базис, определяет изменение базисных переменных,
обусловленное единичным приращением соответствующей небазисной
переменной (в случае если последнюю включить в пробное решение). Так,
например, за счет единичного приращения x
1
в (3.2.3) значения x
5
, x
6
и x
7
уменьшаются соответственно на 4/5, 33/5 и
1
/5. Правильность данного
утверждения можно еще раз проверить на примере третьего пробного
решения, для которого x
1
= 125/12. Следует отметить, что до включения в

53
базис x
1
в системе уравнений (3.2.3) наше внимание привлекала другая
переменная x
2
. В результате же включения в базис x
1
произошло снижение
«значимости» x
2
.
Итерация 3. Завершив вторую симплекс-итерацию, снова рассмотрим
коэффициенты при переменных в строке 0 с целью проверки полученного
решения на оптимальность. Теперь мы видим, что решение может быть
улучшено за счет x
3
. Результаты вычислений, позволяющие выяснить, какая из
переменных должна быть исключена из базиса, представлены в табл. 3.3. В
соответствии с этой таблицей из числа базисных переменных следует
исключить переменную x
4
, вошедшую в решение при первой итерации. В
процессе применения симплексного метода случаи, когда та или иная
переменная при некоторой итерации входит в пробное решение, а затем
исключается из него при одной из последующих итераций, возникают
нередко. Именно это обстоятельство мешает заранее определить
максимальное число симплекс-итераций, которое приводило бы к
решению
любой задачи линейног о программирования.
Таблица 3.3
Итерация 3: включение x
3
в очередной базис (согл. критерию II)
Базисные
перемен-
ные
Рассмат-
риваемое
пробное
Коэффи-
циенты при x
3
Значения
отношений
Минимальное
значение
Следующее
пробное
решение
x
0
1105/12 –11/12
x
1
125/12 5/12 25
x
6
455/12 –13/12 –
x
4
55/12 7/12 55/7 55/7 x
3
=55/7,
Как и в предыдущих итерациях, пронормируем коэффициент при x
3
в
строке 3 путем деления обеих частей соответствующего уравнения на 7/12.
Система уравнений примет вид
1x
0
+
6
1
x
1
–
12
11
x
2
+
4
9
x
5
+
12
7
x
7
=
12
1105
(строка 0),
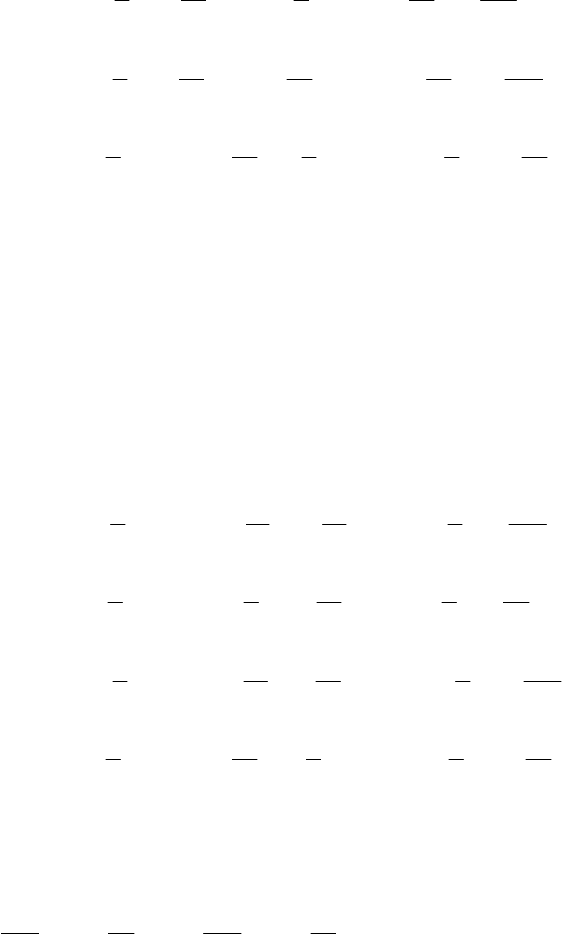
54
1x
1
+
6
5
x
2
+
12
5
x
3
+
4
5
x
5
–
12
1
x
7
=
12
125
(строка 1), (3.2.6)
–
6
7
x
2
–
12
13
x
3
–
4
33
x
5
+1x
6
+
12
5
x
7
=
12
455
(строка 2),
7
2
x
2
+ 1x
3
+
7
12
x
4
–
7
3
x
5
+
7
1
x
7
=
7
55
(строка 3).
Теперь исключим x
3
из уравнений в строках 0, 1 и 2, действуя по
следующей схеме:
1) умножить строку 3 на 11/12 и результат сложить со строкой 0;
2) умножить строку 3 на (–5/12) и результат сложить со строкой 1;
3) умножить строку 3 на 13/12 и результат сложить со строкой 2.
В результате получим
1x
0
+
7
3
x
2
+
7
11
x
4
+
7
13
x
5
+
7
5
x
7
=
7
695
(строка 0),
1x
1
+
7
5
x
2
–
7
5
x
4
+
7
10
x
5
–
7
1
x
7
=
7
50
(строка 1), (3.2.7)
–
7
6
x
2
+
7
13
x
4
–
7
61
x
5
+1x
6
+
7
4
x
7
=
7
325
(строка 2),
7
2
x
2
+ 1x
3
+
7
12
x
4
–
7
3
x
5
+
7
1
x
7
=
7
55
(строка 3).
Итерация 4. В строке 0 системы уравнений (3.2.7) все коэффициенты
положительны и, следовательно, согласно критерию I, полученное решение
x
0
=
7
695
, x
1
=
7
50
, x
6
=
7
325
, x
3
=
7
55
является оптимальным. Таким образом, на
шаге 2 вычисления прекращаются. Остается убедиться, что полученные
значения переменных действительно удовлетворяют (3.2.1).
Резюме. В кратком изложении симплексный метод состоит в следующем:
Шаг 1. Выбирается исходный базис.
Шаг 2. Используется критерий I. Если рассматриваемое пробное решение
не является оптимальным, осуществляется переход к шагу 3. В противном
случае вычисления прекращаются
.
Шаг 3. Выполняется процедура, предписанная критерием II.
Шаг 4. Сменяется базис, после чего возвращаются к шагу 2.

55
Вычислительные процедуры, выполняемые в соответствии с симплекс-
алгоритмом, легко интерпретировать геометрически в пространстве решений.
При этом каждый пробный базис соответствует вершине выпуклого
полиэдрального множества допустимых решений. Переход от одного базиса к
другому геометрически выглядит как переход от одной экстремальной точки к
другой (причем смежной) экстремальной точке. Таким образом, можно
утверждать, что
поиск оптимального решения симплексным методом
заключается в последовательном восхождении вдоль ребер упомянутого
многогранника от одной его вершины к соседней.
Оптимальность. Поскольку соотношения (3.2.7) получены из исходных
уравнений (3.2.1) с помощью эквивалентных алгебраических действий,
системы уравнений (3.2.1) и (3.2.7), несмотря на внешнее различие,
представляют собой математическую формулировку одной и той же задачи.
Предположим, что
с самого начала мы имеем (3.2.7). После простого
преобразования строки 0 целевую функцию можно записать в виде
x
0
=
7
695
–
7
3
x
2
–
7
11
x
4
–
7
13
x
5
–
7
5
x
7
.
(3.2.8)
При любом отличном от нуля допустимом значении хотя бы одной из
небазисных переменных x
2
, x
4
, x
5
или x
7
целевая функция принимает, согласно
(3.2.8), значение, меньшее по сравнению с полученным выше, т. е. меньшее по
сравнению с
695
/
7
.
Коэффициенты при переменных в окончательном варианте строки 0
иногда называют скрытыми издержками. Каждый коэффициент определяет
отклонение значения целевой функции от оптимального при увеличении
значения соответствующей небазисной переменной на единицу; при этом
предполагается, что базис, построенный на заключительной итерации,
остается допустимым. Коэффициенты при свободных переменных иногда
называют скрытыми ценами (объективно-обусловленными
оценками); смысл
этих коэффициентов подробно обсуждается в следующем параграфе.
Положим, например, x
2
= 1. Это повлечет за собой снижение значения x
0
на

56
3
/
7
. При этом значения базисных переменных также изменятся, в чем можно
убедиться с помощью соотношений, приведенных в строках 1, 2 и 3.
Рассмотрим базисную переменную в строке 1 системы уравнений (3.2.7):
x
1
=
7
50
–
7
5
x
2
+
7
5
x
4
–
7
10
x
5
+
7
1
x
7
.
(3.2.9)
Полагая x
2
= 1, мы уменьшаем значение x
1
на
5
/
7
.
Альтернативные оптимальные решения. В гл. 2 было показано, что
задача линейного программирования может иметь несколько оптимальных
решений. Графическое рассмотрение для двумерного случая показало, что
если линейная модель имеет более чем одно оптимальное решение, то она
имеет бесконечное число оптимальных решений. Оказывается справедливым
обобщение данного утверждения и на случай большего числа измерений
.
Пытаясь разобраться, в силу чего это происходит, рассмотрим следующий
пример. Предположим, что вместо (3.2.1) мы имеем другую модель, в которую
входит новая переменная x
8
. В строки системы уравнений (3.2.1) внесены
следующие изменения:
–2x
8
(строка 0),
+lx
8
(строка 1),
+9x
8
(строка 2), (3.2.10)
+0,2x
8
(строка 3).
На заключительной итерации мы будем иметь следующие дополнения к
строкам системы уравнений (3.2.7):
0x
8
(строка 0),
+
7
8,9
x
8
(строка 1),
+
7
8,2
x
8
(строка 2), (3.2.11)
–
7
8,2
x
8
(строка 3).
Нетрудно убедиться, что если x
8
включить в базис, то, согласно критерию
II, x
1
выйдет из базиса и альтернативное оптимальное базисное решение

57
примет следующий вид:
x
0
=
7
695
, x
8
= 1,5
8,9
50
= , x
6
= 39,44
8,97
3045
=
⋅
, x
3
= 9,9
8,97
679
=
⋅
(3.2.12)
при x
1
= x
2
= x
4
= x
5
= x
7
= 0. Легко показать, что любое положительно-
взвешенное среднее двух полученных оптимальных базисных решений также
является альтернативно допустимым оптимальным решением
x
0
=
7
695
,
x
1
= w(
7
50
)+(1– w)0,
x
3
= w(
7
55
)+(1– w)9,9, (3.2.13)
x
6
= w(
7
325
)+(1– w)44,39,
x
8
= w(0)+(1– w)5,1,
где w — весовой коэффициент, удовлетворяющий условию 0 < w < 1.
Положим для примера w = 0,5 и вычислим с помощью (3.2.13) x
1
, x
3
, x
6
и x
8
.
Легко показать, что полученные значения этих переменных удовлетворяют
исходным ограничениям и определяют оптимальное значение целевой
функции, равное
695
/
7
.
3.3. Полнота алгоритма
При некоторых итерациях вычислительные процедуры, предписанные
симплекс-критериями I и II, в части, касающейся перехода от одного базиса к
другому, могут оказаться неоднозначно определенными. Например, когда в
результате оценки коэффициентов в строке 0 две или более двух переменных
являются по критерию I в равной степени «перспективными» с точки зрения
улучшения пробного
решения, выбор одной из этих переменных
осуществляется произвольным образом. Например, можно взять переменную с
наименьшим значением индекса или переменную, которая по некоторым
58
предварительным соображениям должна войти в базис на последней итерации.
Если, согласно критерию II, две или более двух переменных
промежуточного базиса должны одновременно принять нулевые значения в
силу включения в очередной базис новой переменной, из старого базиса
исключению подлежит только одна из них. Другие из упомянутых
переменных остаются в базисе, принимая при этом
нулевые значения. Базис,
получаемый в результате такой замены, называется вырожденным.
Если на этапе применения критерия II при выполнении какой-либо
итерации обнаруживается, что ни в одну из строк переменная, включенная в
очередной базис, не входит с положительным коэффициентом, то
оптимальное решение является неограниченным. В этом случае значение
новой базисной переменной можно
(без нарушения условия
неотрицательности остальных переменных) выбирать сколь угодно большим,
что приводит к неограниченному возрастанию значения целевой функции.
Таким образом, сделанное ранее предположение относительно
ограниченности оптимального значения целевой функции можно теперь
отбросить. Симплексный алгоритм сам позволяет определять те случаи, когда
оптимальное решение оказывается неограниченным.
Исходный базис. Вернемся к вопросу о
выборе исходного базиса,
позволяющем начать вычислительную процедуру в соответствии с
симплексным алгоритмом. Поскольку в модели, рассмотренной в предыдущем
разделе, каждое из ограничений имеет вид
0),,...,1(,
1
≥=≤
∑
=
i
n
j
ijij
bmibxa , (3.3.1)
введение в рассмотрение свободных переменных (по одной свободной
переменной в каждом соотношении, задающем соответствующее
ограничение) и включение только этих переменных в исходный базис
позволяет просто выполнить шаг 1 (т.е. построение первого пробного
решения). Как было показано в гл. 2, соотношением (3.3.1) не охватываются
все возможные типы ограничений, встречающихся в линейных
