Гельруд Я.Д. Линейное программирование. Учебно-методический комплекс

Подождите немного. Документ загружается.

Г. В случае r= r

выполняется стандартная процедура замены базиса,

модифицирующая строку k.

Д. Если r= r

, то выполняется стандартная процедура замены базиса,

модифицирующая строку k'; затем в строке k' осуществляется замена x

↔x'

[см. (2)].

После выполнения заключительной итерации решение будет содержать

либо x

, либо x'

. Если переменная x

окажется небазисной, се значение

приравнивается нулю. Если же x

войдет в базис, то ее пробное значение

является оптимальным. Если переменная x'

окажется небазисной, то

оптимальное значение x

= 1. Если в базис войдет x'

, то оптимальное значение

равняется 1 – x'

. Ниже приводится пример на применение только что

сформулированного критерия.

Задачи с ограниченными сверху переменными можно решать с помощью

несколько видоизмененного двойственного симплекс-алгоритма. Критерии I и

II остаются при этом без изменений; подстановка типа (5.7.3) или (5.7.4)

производится по мере необходимости на различных этапах итерационного

процесса. Читателю предоставляется возможность продемонстрировать

эффективность такого алгоритма

самостоятельно. Вычислительный процесс

можно начать, выбрав в качестве пробного решения модифицированной

задачи (за счет введения для переменных ограничений сверху) оптимальное

решение (которое предполагается конечным) соответствующей задачи, в

которой значения переменных не ограничены сверху, причем такое решение,

которое не удовлетворяет дополнительным ограничениям, накладываемым на

управляемые переменные.

Пример. Рассмотрим задачу:

максимизировать 4

+ 10x

+ 9x

+ 11x

(5.7.5)

при ограничениях

+ 1x

+ 2x

+ 1x

≤

100

+ 5x

+ 10x

+ 15x

≤

275

, (5.7.6)

0 ≤ x

≤ 1 (j = 1, 2, 3, 4).

В первое и второе соотношения введем свободные переменные x

и x

соответственно. Заметим, что верхняя граница для значений этих переменных

не равна единице. Однако это нисколько не усложняет вычислительную

процедуру.

Начальное базисное решение включает упомянутые выше свободные

переменные; это решение приведено в табл. 5.3. Согласно симплекс-критерию

I (максимизация), в очередной базис входит переменная x

. Поскольку

коэффициенты при x

не отрицательны,

r = r

= min(

1615

275

⋅

240

275

>1. (5.7.7)

Следовательно, согласно симплекс-критерию II (при значениях

переменных, ограниченных сверху), необходимо произвести подстановку x

– x

′

(итерация 2). При этом x

′

входит в очередное пробное решение, а

пробные значения базисных переменных соответствующим образом

изменяются.

На следующей итерации в базис вводится x

. При этом снова все

коэффициенты при x

оказываются неотрицательными и, следовательно,

r = r

= min(

165

⋅

, (5.7.8)

101

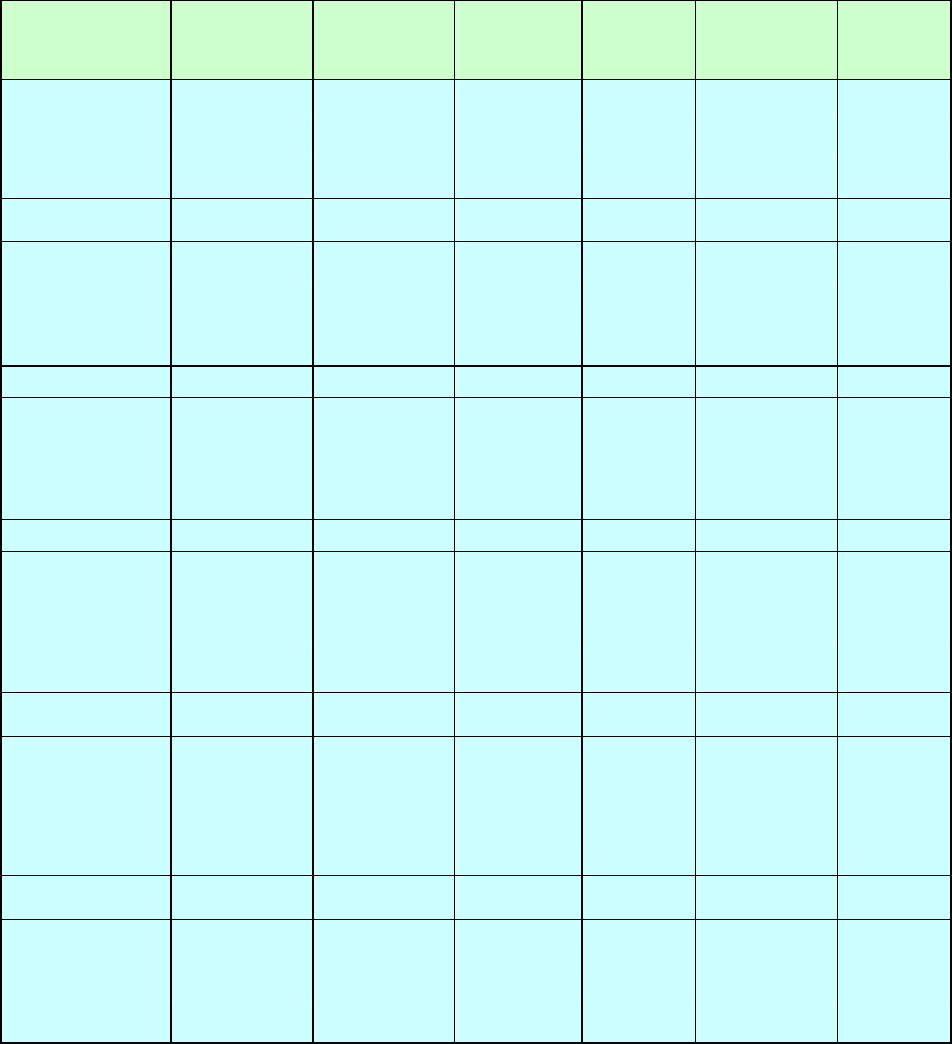
Таблица 5.3

Номер

ите

ации

Базис

Пробные

значения

0 –4 10 –9 –11

1 x

5/2 1 1 1 1

257/16 3 5 10 –15

11 –4 –10 –9 11

2 x

3/2 1 1 1 –1

17/16 3 5 10 –15

105/8 –2 2 11 –19

3 x

103/80 2/5 –1/5 –1 2

17/80 3/5 1/5 2 –3

1449/80 –9/5 11/15 –5/3 19/3

4 x

61/80 4/5 –1/15 1/3 –2/3

21/80 –1/5 –1/15 –2/3 1/3

1269/164 9/4 7/12 –11/12 29/6

5 x

61/64 5/4 –1/12 5/12 –5/6

29/64 1/4 –1/12 –7/12 1/6

331/16 13/7 5/7 11/7 32/7

6 x

9/16 10/7 –1/7 –5/7 –5/7

15/16 –3/7 1/7 12/7 –2/7

Сводная симплекс-таблица для задачи с ограниченными значениями

переменных, т. е. x

входит в базис вместо x

. После обычной процедуры

замены опорного плана получаем значения всех коэффициентов модели (как

результат выполнения итерации 3).

102

На данном этапе необходимо ввести в базис переменную х'

; при этом

имеем

028

103

⋅

, r

1)80/17(

−

, r = r

. (5.7.9)

Следовательно, переменная х'

(значение которой ограничено сверху)

входит в базис вместо х

. Значит, после замены базиса следует произвести

подстановку х

= 1 – х'

. Именно в этом заключается итерация 4.

Легко убедиться, что на итерации 5 вместо х

в базис войдет х

, так как

r=r

<1. Можно показать, что следующий шаг будет заключаться в том, чтобы

вместо х'

ввести в базис х

; при этом производится замена х

= 1 – х'

, т. е.

выполняется итерация 6, результаты которой также представлены в табл. 5.3.

Оптимальные значения переменных х

и х

приведены на пересечении шестой

составной строки и третьего столбца табл.5.3. Оптимальное значение х

равняется единице, так как переменная х'

является небазисной.

При ознакомлении с таблицей, содержащей данные для всех итераций,

следует обратить внимание на то, что х

входит вначале в решение как

переменная, значение которой ограничено сверху, и, следовательно, должна

быть произведена подстановка х'

= 1 – х

. Затем в базис вводится х'

. На

итерации 4 переменная х'

исключается из базиса и, поскольку значение

данной переменной ограничено сверху, производится замена х'

= 1 – х

Тема 6. Основы целочисленного линейного программирования.

6.1. Основные определения

В этой главе снимается допущение делимости и рассматриваются задачи,

в которых некоторые или все переменные могут принимать только

целочисленные значения.

Рассмотрим следующую модель:

103

Оптимизировать F =

∑

Æ max( min) (6.1.1)

при ограничениях:

∑

≤ b

(i=1,2,…,m), (6.1.2)

≥ 0 (j=1,2,…n). (6.1.3)

– целые, j = 1, 2, . . ., p (≤n). (6.1.4)

Задачи оптимизации такого класса называются задачами целочисленного

(или диофантового, или дискретного) программирования. Если р = п, т. е. все

переменные должны быть целыми числами, то модель

определяет полностью

целочисленную задачу. В противном случае, т. е. когда р < п, имеем частично

целочисленную задачу.

Задача целочисленного программирования отличается от задачи линейного

программирования условиями дискретности. В общем случае условие (6.1.4)

накладывает дополнительные ограничения, вследствие которых максимальное

значение целевой функции задачи целочисленного программирования

оказывается меньше значения целевой функции соответствующей задачи

линейного программирования

6.2. Область применения целочисленного программирования

1. Использование оборудования. Переменными x

можно обозначить

единицы оборудования, которые должны функционировать в течение

планового периода, описываемого моделью. Дробное значение x

может и не

иметь смысла (т. е. оказаться нереализуемым) в рамках реальной задачи

принятия решения. В таком случае на значения x

приходится наложить

требование целочисленности.

2. Затраты на подготовку производства. Может возникнуть

необходимость рассмотрения операции, выполнение которой связано с так

называемыми постоянными затратами (или затратами на подготовку

104

производства) С

всегда, когда соответствующее значение x

> 0, причем C

не

зависит от фактического значения x

. Так, например, если x

определяет

часовой показатель использования объема доменной печи на

металлургическом заводе, то C

соответствует затратам на задувку домны и на

ее нагрев до заданной температуры.

Постоянные затраты можно учесть в

модели математического программирования за счет введения целочисленных

переменных.

3. Размеры партий. При разработке некоторых производственных планов

на значения x

могут накладываться ограничения вида x

= 0 или x

≥ L

. Так,

например, величина x

может представлять собой количество определенных

изделий, которое нужно выпустить в течение периода t, a L

– минимально

возможный размер партии этих изделий. Подобное условие является

примером ограничения вида «или–или», и его можно формально ввести в

модель, используя целочисленные переменные.

4. Решения типа «да – нет». Может возникнуть необходимость

определения ситуаций «или – или» иного характера. С этой целью на

переменные x

накладываются ограничения x

= 1 или x

= 0, соответствующие

решениям «принять» или «отвергнуть» либо «да» или «нет». В качестве

примера можно принять, что x

= 1 соответствует решению строить новое

промышленное предприятие, или организовать сбыт продукции в новом

районе, или приобрести новое предприятие, или продать имеющееся в

распоряжении фирмы оборудование. Довольно часто альтернативы такого

рода относятся к разряду решений о распределении капиталовложений,

поскольку их реализация связана с крупными затратами денежных средств и

ресурсов. Это можно считать

основной причиной, объясняющей, почему

целочисленное программирование играет столь важную роль в

организационных решениях. Оптимальное решение задачи распределения

капиталовложений может принести фирме гораздо большую прибыль, чем

приближенное или угаданное. Так, например, может оказаться, что фирме,

производящей цемент и имеющий 25 предприятий, удастся значительно

105

повысить получаемую прибыль, сократив число своих предприятий до 20 или

менее при условии, что такое мероприятие предусматривается оптимальным

планом. Сокращение накладных расходов при уменьшении числа предприятий

может с избытком компенсировать рост транспортных затрат, если

размещение оставшихся предприятий также подчиняется оптимальному

плану.

В ряде других задач принятия решений может потребоваться построение

моделей

целочисленного программирования. Один класс таких задач связан с

решениями, определяющими выбор упорядочений, календарных планов

(расписаний) и маршрутов. Примером задачи, принадлежащей к этому классу,

может служить задача коммивояжера. В этой задаче нужно отыскать

кратчайший маршрут коммивояжера, который должен побывать в каждом из п

городов, причем маршрут начинается и заканчивается городом 1. В

качестве

другого примера задач указанного класса можно взять задачу составления

расписания обработки деталей на станках. Наиболее простым вариантом

этой задачи является случай, когда каждая из п деталей должна

обрабатываться на каждом из k станков. Предположим, что деталь нельзя

обрабатывать на станке j, пока не закончена ее обработка на станке j

–1.

Предположим, далее, что время обработки каждой детали на каждом станке

строго фиксировано. Тогда оптимальная последовательность определяется

расписанием обработки, минимизирующим общую продолжительность

обработки всех деталей на всех станках. Другими примерами задач

упорядочения, выбора маршрута и календарного планирования являются

задачи баланса сборочных линий, сетевого планирования при ограниченных

ресурсах, предупредительного ремонта при ограничениях

на рабочую силу и

диспетчирования автотранспорта.

Имеется бесчисленное множество других примеров, относящихся прежде

всего к задачам распределения ресурсов в течение короткого периода времени

(суток, недели, месяца), которые также можно отобразить в виде моделей

целочисленного линейного программирования. Иллюстрацией таких примеров

106

могут служить задачи выбора автомашин различных габаритов для доставки

заданных количеств определенных грузов; задачи календарного планирования

работы бумагоделательных машин и прокатных станов при различных

номенклатурах продукции, заданной требованиями заказчика; задачи

распределения крупных заказов по предприятиям фирмы, отличающимся

производственной мощностью, эффективностью и издержками производства.

Зная методы построения моделей линейного программирования, легко

сформулировать

такие задачи определения ресурсов в виде моделей

целочисленного программирования. Поэтому в данной главе подобные задачи

более подробно не рассматриваются.

Несмотря на большое внимание, уделяемое в литературе по исследованию

операций задачам упорядочения, календарного планирования и выбора

маршрута, которые отображаются моделями целочисленного

программирования, до сих пор эти модели находят лишь ограниченное

применение

на практике. Одна из причин, вычислительные трудности,

оказывавшиеся настолько значительными, что затраты, связанные с

получением решений для моделей реальной размерности, превышают эффект,

достигаемый за счет реализации найденного решения.

Задачи упорядочения, календарного планирования и выбора маршрута

являются частными случаями комбинаторных задач.

Комбинаторная оптимизационная задача состоит в отыскании среди

конечного множества альтернатив одной

, которой отвечает экстремальное

значение принятой целевой функции.

6.3. Методы решения задач целочисленного программирования

Существует несколько алгоритмических методов решения задач

целочисленного программирования, которые можно непосредственно

применять к комбинаторным моделям без их предварительного

преобразования в целочисленные модели.

107

Следует отметить, что в моделях математического программирования

вычисления значительно проще в случае непрерывных переменных, чем в

случае дискретных. Это весьма убедительно демонстрирует следующий

простой пример, который приводится ниже.

Рассмотрим модель:

максимизировать 21x

+ 11x

(6.3.5)

при ограничениях

+ 4х

≤ 13, (6.3.6)

и x

— неотрицательные целые. (6.3.7)

Почти сразу можно определить, что единственным оптимальным

решением является х

= 0, x

= 3. Ясно, что поскольку размерность этой задачи

чрезвычайно мала, то для отыскания решения и его проверки можно

воспользоваться самыми различными методами. Однако, поскольку здесь

ставится цель продемонстрировать относительную сложность решения задач

целочисленного программирования средней и большой размерности, сразу же

исключим из рассмотрения любую схему, подходящую для решения

некоторой частной задачи, а

также общие алгоритмы, позволяющие находить

решения лишь для задач малой размерности.

Существует один подход к отысканию целочисленных решений, который

часто предлагают начинающие. Этот подход сводится к тому, что сначала не

учитываются условия целочисленности, и определяется оптимальное решение

обычной задачи линейного программирования. Если полученное решение

удовлетворяет ограничениям целочисленности, то оно является

оптимальным

решением и исходной целочисленной задачи. В противном случае

предлагается переходить к целочисленному решению с помощью округления

решения обычной задачи линейного программирования до целых чисел.

Предположим, что такой подход применяется к примеру (6.3.5) – (6.3.7).

Оптимальное дробное решение соответствующей задачи линейного

программирования равно x

и x

= 0. Очевидное округленное решение

равно x

= 2 и x

= 0, что является недопустимым. Решение с округлением в

108

«меньшую сторону» будет x

= 1 и x

= 0. Это решение допустимо, но оно

очень далеко от оптимального. Трудно представить себе даже возможность

существования общего, имеющего практическую ценность метода округления

дробного решения для задач средней и большой размерности, который давал

бы оптимальное целочисленное решение.

Еще более неприятная особенность, свойственная задачам целочисленного

программирования, заключается в том, что нет простого способа

позволяющего определить, является ли данное допустимое решение

оптимальным. В этом одно из важных отличительных pазличий между

задачами целочисленного и линейного программирования. Чтобы показать это

различие, предположим, что в приведенной выше задаче (6.3.5) – (6.3.7) нужно

проверить, является ли решение x

= x

= 1 оптимальным. С этой целью нужно

проверить, соответствует ли это решение какому-либо локальному оптимуму в

том смысле, что значение целевой функции не улучшается в любой соседней

целочисленной точке (или в узле решетки) x

= 1 + d и x

= 1 + е, где d, e = —1;

0; 1. Покажите, что допустимыми соседними точками в данном случае

являются точки (x

= x

= 0; x

= 0 и x

= 1; x

= 0 и x

= 2; x

= 1 и x

= 0).

Покажите также, что решение x

= x

= 1 на самом деле лучше всех этих

решений, но, тем не менее, не является оптимальным. Следовательно,

некоторая точка может быть локально оптимальной по отношению к соседним

точкам решетки, но все-таки не соответствовать глобальному оптимуму.

Сейчас уже пора задать вопрос, сводится ли наилучший общий метод

решения к простому перебору всех допустимых

решений и последующему

выбору наилучшего из них. Если имеется всего несколько допустимых

решений, то такой метод действительно проще реализовать, чем любой из

рассмотренных далее в этой главе алгоритмов. В ряде случаев, встретившихся

на практике, именно такой метод и применялся. Однако, как правило, метод

полного перебора оказывается неработоспособным. Это объясняется тем, что

число допустимых решений не всегда конечно, но даже тогда, когда условие

конечности не нарушается, это число обычно огромно. Рассмотрим, например,