Фурсов В.А. Лекции по теории информации

Подождите немного. Документ загружается.

121

Введя в пространстве состояний преобразование координат









t t



s Ps

умножив (14.3) слева на

, систему (14.3) (14.4) представим в виде













t t t



  

Ps PAP s PBu

, (14.8)













t t t



 

y CP s Du

, (14.9)

Далее введя обозначения





A PAP



B PB





C CP



D D

с учетом того, что в соответствии с используемым преобразованием координат









1 1

t t

  

Ps s ,

уравнения (14.8), (14.9) можно переписать в виде













t t t

  

s As Bu

, (14.10)













t t t

 

y Cs Du

. (14.11)

Системы (14.3), (14.4) и (14.10), (14.11) описывают различные, но совпа-

дающие по входу и выходу ЛПМ. Такие ЛПМ называют подобными. Путем

преобразований подобия может быть построена ЛПМ, имеющая минимальное

число задержек. Такая ЛПМ называется минимальной.

Минимальная ЛПМ может быть определена в результате выполнения сле-

дующей последовательности шагов [2].

1. Строится так называемая диагностическая матрица (наблюдаемости)

k 

 



 

K C CA CA  .

2. Из линейно независимых строк диагностической матрицы формируется

матрица

и осуществляется преобразование подобия:





A TAT



B TB





C CT



D D

Результатом преобразования будет минимальная ЛПМ.

Если ЛПМ с матрицей

имеет подобную ЛПМ с матрицей

, то она

имеет и естественную нормальную форму

. Каждая подматрица

 



A мат-

рицы

, имеющая вид (14.6), соответствует некоторой канонической ЛПМ.

122

Каноническая форма является минимальной ЛПМ. Следовательно, в ре-

зультате преобразования подобия исходная ЛПМ всегда может быть представ-

лена в виде совокупности ЛПМ, каждая из которых соответствует элементар-

ному делителю





, 1,

x i r



 в разложении многочлена







14.5 Понятие простой автономной ЛПМ

Рассмотрим каноническую (минимальную) ЛПМ, имеющую сопровож-

дающую матрицу вида (14.6) при







u . ЛПМ с нулевым входным воздейст-

вием: называются автономными. Выходные последовательности на всех выхо-

дах ЛПМ, являющихся компонентами вектора

, в этом случае формируются

по соотношению (14.5) под действием начальных условий.

Для автономной ЛПМ можно выполнить преобразование подобия для ка-

ждого отдельного выхода (компонента вектора

) исходной ЛПМ. При этом из

ЛПМ с

выходами будет получено

различных ЛПМ с одинаковыми матри-

цами

и различными матрицами

, представляющими собой отдельные стро-

ки исходной

m n



– матрицы

Каждая из построенных таким образом

схем называется простой авто-

номной ЛПМ (простой АЛПМ), а матрица

 



A каждой простой АЛПМ имеет

вид (14.6) и является сопровождающей для многочлена обратной связи





1 1 0

...

k k

x x x x

   



    

Матричные соотношения, описывающие соответствующую матрице

 



A и

указанному многочлену







простую автономную ЛПМ при





1,0, ,0

C



имеют вид:





 





 

1 1

0 1 1

1 0

k k k

s t s t

  





   

 

   

 



   

 

   

 

   

 

   



      

 

 

 





 

1,0,...,0

s t

y t

s t

 

 



 

 



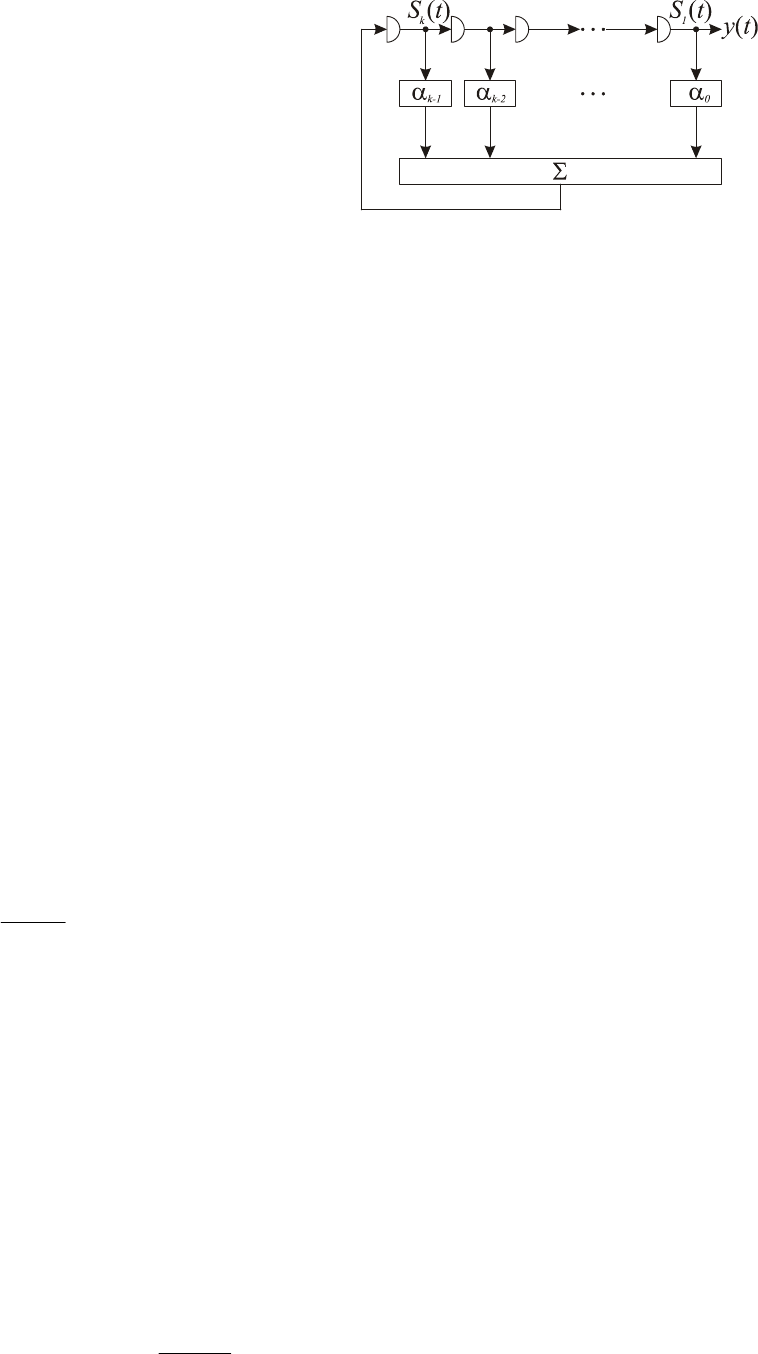
123

Приведенные равенства можно представить

в виде схемы, показанной на рисунке 14.3.

Непосредственно по схеме можно за-

писать соотношение для формирования вы-

ходной последовательности простой

АЛПМ:

1 1 1 1 0

t k k t k t t

y y y y

  

    

   



. (14.12)

Нетрудно заметить, что символы выходной последовательности являются ли-

нейной комбинацией начального состояния АЛПМ.

14.6 Формирование разрешенных комбинаций циклического

кода с помощью АЛПМ

В разделе 12.5 мы рассмотрели два способа формирования комбинаций и

декодирования циклических кодов. Рассмотрим еще один способ, который наи-

более удобно реализуется с помощью АЛПМ.

Определим многочлен обратной связи







как частное от деления



на образующий многочлен. В силу свойств





g x

такой целый полином сущест-

вует:

 

1 1 0

...

k k

x x x x

g x

   





     

. (14.13)

Многочлен (14.13) называют также генераторным полиномом. Для этого поли-

нома можно построить сопровождающую матрицу

 



A вида (14.6) и соответ-

ствующую ей АЛПМ.

Если начальное состояние АЛПМ (рисунок 14.3) соответствует исходной

информационной последовательности, на выходе будет сформирована комби-

нация, первые

символов которой информационные, а следующие за ними

n k



являются линейной комбинацией предыдущих символов:

, 1,

j k i j i

а j n k





 



  



. (14.14)

Рис. 14.3 – Схема простой

АЛПМ

124

где



– двоичные коэффициенты многочлена обратной связи АЛПМ (14.13)

(генераторного многочлена). Таким образом, с использованием АЛПМ может

быть построен систематический циклический код.

14.7 Образующая матрица АЛПМ

Если







– многочлен обратной связи (генераторный многочлен), удов-

летворяющий (14.13), то образующий многочлен степени

m n k

 

определяет-

ся как

 

1 0

...

g x g x g x g





    

Тогда, в соответствии с описанным в разделе 13.6 первым способом, может

быть построена образующая матрица (13.12) соответствующего циклического

кода:

1 0

0 0

m m

n k

m m

g g g



 

 



 

 

 

 

      

 

Разделим образующую матрицу

n k

на два блока





1 2



M M M



так, что-

бы

была квадратной. В силу неприводимости многочлена





g x

ее диаго-

нальные элементы отличны от нуля, следовательно, матрица

является не-

вырожденной.

Последовательность информационных символов

можно представить

как линейную комбинацию строк матрицы

 

A v M

, откуда





v A M

. (14.15)

С другой стороны, избыточный код является той же линейной комбинацией

строк матрицы





1 2

T T

  

A v M v M M



Подставляя в это равенство

из (14.15) имеем

125





1 1

1 1 2 1 2

n k k

 

 

 

 

A A M M M A E M M 

Матрица

1 2 ,

k n k



 

 

 

M E M M E P 

является образующей матрицей АЛПМ с

многочленом обратной связи







. Очевидно, что с ее использованием может

быть сформирован систематический код.

Подводя итог, следует заметить, что в настоящей лекции, посвященной

изучению линейных последовательных машин, мы привели мало новых сведе-

ний, посвященных собственно теории кодирования. Цель этого раздела состоя-

ла в том, чтобы показать связь теории кодирования с общей теорией линейных

систем. Нам представляется это чрезвычайно важным для понимания общих

принципов построения кибернетических систем.

126

Лекция 15

Обнаружение и различение сигналов

15.1 Постановка задачи обнаружения сигналов

при наличии помех

Задача приемного устройства – извлечение из принятого сигнала макси-

мума полезной информации. Для этого последовательно решаются, по крайней

мере, две задачи [9]:

1) обнаружение (принятие решения о наличии сигнала);

2) восстановление (определение параметров сигнала).

Задача определения параметров сигналов рассматривается в следующей лек-

ции. Здесь рассмотрим методы обнаружения сигналов.

Принимаемый сигнал будем представлять вектором

, компоненты кото-

рого являются отсчетами, каждый из которых представляет собой сумму отсче-

тов компонентов векторов полезного сигнала

и помехи

. Ясно, что по при-

нятому вектору

мы не можем однозначно судить о векторе

. О переданном

в действительности сигнале

можно судить лишь с некоторой вероятностью





X Y

В общем случае в соответствии с формулой Байеса апостериорная плот-

ность вероятности вектора

определяется как

 









 

w w



X Y X

X Y

, (15.1)

где





– априорная плотность вероятности вектора





Y X

– условная

плотность вероятности вектора

при условии, что вектор

известен, а













w w w d





Y X Y X X

– безусловная плотность вероятности вектора

, где

– пространство передаваемого сигнала.

Если вектор

имеет конечное число значений, по аналогии с (15.1)

127

 









 









   

j j

p w p w

p x w x



 



X Y X X Y X

X Y

, (15.2)

где





– априорная, а





X Y

– апостериорная вероятности вектора X.

Таким образом, для определения апостериорной плотности





X Y

и/или

вероятности





X Y

необходимо знать априорные плотность





и/или ве-

роятность





, а также условную плотность





Y X

, которая при известном

(измеренном)

зависит только от

и обозначается













w L

Y X X

. (15.3)

Функция





называется функцией правдоподобия. Эта функция может иметь

конечное (в случае дискретного

) или бесконечное (в случае непрерывного

) число значений.

Задача обнаружения сигнала заключается в принятии одной из возможных

взаимно исключающих альтернатив (гипотез): гипотезы

о том, что



X –

сигнал есть, или гипотезы

о том, что



X – сигнал отсутствует. В матема-

тическом отношении эта задача эквивалентна задаче оптимального разбиения

пространства принимаемых сигналов

на области

. Если принятый век-

тор

окажется в области

, принимается гипотеза

, если же он окажется в

области

, принимается гипотеза

Для построения правила принятия решения о выборе гипотезы (разбиения

пространства принимаемых сигналов) в рассмотрение вводится так называемая

функция (отношение) правдоподобия:





 





 

1 1

0 0

L x w x



 

. (15.4)

Рассмотрим различные критерии принятия решений, формулируемые в терми-

нах отношения правдоподобия (15.4).

128

15.2 Обнаружение по критерию максимального правдоподобия

По этому критерию наиболее правдоподобным считается то значение

для которого функция правдоподобия максимальна. Поскольку в задаче обна-

ружения рассматривается две альтернативы, существо дела сводится к сравне-

нию





L x





L x

. При этом решающее правило в терминах отношения прав-

доподобия принимает вид:

если





 

L x



 

, то



X , (15.5)

если





 

L x



 

, то



X , (15.6)

Важное достоинство критерия максимума правдоподобия состоит в том, что в

данном случае не требуется знание априорных вероятностей





p x





p x

сиг-

нала

15.3 Обнаружение сигналов по критерию максимума

апостериорной вероятности

В соответствии с этим критерием сравниваются значения апостериорных

вероятностей





p x





p x

если





 

p x



, то



X , (15.7)

если





 

p x



, то



X . (15.8)

С использованием формулы Байеса (15.2) и равенства (15.3) отношение

апостериорных вероятностей выражается через отношение правдоподобия:





 









   





 

1 1 1 1

0 0 0 0

p x p x L x p x



 

При этом критерий можно записать следующим образом:

если





 

p x





, то



X , (15.9)

129

если





 

p x





, то



X . (15.10)

Решающее правило можно также представить в виде:

если





 

p x

 

 

, то



X , (15.11)

если





 

p x

 

 

, то



X , (15.12)

где



– пороговое значение отношения правдоподобия. Критерий максимума

апостериорной вероятности применяется в случае, когда известны априорные

вероятности





p x





p x

сигнала

15.4 Информационный критерий обнаружения

С точки зрения теории информации наиболее предпочтительно то значение

, относительно которого в

содержится больше информации:

















   

 

1 0 2 1 2 1

2 0 2 0

1 0

2 2 2

0 1 0

, , log log /

log log /

log log log .

/ /

I x I x p x p x

p x p x

p x

p x p x p x



    

 

 

 

   

 

  

Y Y Y

Y Y

(15.13)

В соответствии с информационным критерием (15.13), если логарифм отноше-

ния правдоподобия положителен, следует принять гипотезу

(



X ), если

отрицателен или равен нулю –

(



X ).

Нетрудно заметить, что этот критерий совпадает с критерием максималь-

ного правдоподобия (15.5), (15.6).

15.5 Обнаружение по критерию Неймана-Пирсона

При решении задачи обнаружения сигналов могут иметь место ошибки

двух типов:

1) ошибка первого рода – «ложная тревога» (при отсутствии сигнала приня-

та гипотеза

–



X ), вероятность которой определяется как

130





w x d







Y Y

; (15.14)

2) ошибка второго рода «пропуск сигнала» (при наличии сигнала принята

гипотеза

–



X ), вероятность которой





w x d







Y Y

. (15.15)

При этом общая вероятность ошибочного решения









0 1ош

p p x p x

 

  . (15.16)

В соответствии с критерием Неймана–Пирсона наилучшим считается ре-

шение, при котором





/ min

w x d



 



Y Y ,

при условии, что





w x d

 

 



Y Y ,

где



– заданная величина.

Рассмотрим решение указанной задачи для простейшего случая, когда



– скаляр. При этом

 

w y x dy











 

w y x dy









а функция Лагранжа принимает вид

 

1 0

/ /F w y x dy w y x dy



 

  

 

 

 



 

Необходимые условия экстремума





0, 0

F F

     

 









0 1 0 0

/ / 0

w x w x

  

  

, (15.17)

 

/w y x dy











. (15.18)

В соответствии с (15.17)









0 1 0 0

/ /w x w x



  

. (15.19)