Fujita S., Ito K., Godoy S. Quantum Theory of Conducting Matter

Подождите немного. Документ загружается.

5.2 Two-Particle Composites 63

we obtain

= B

†

(1 −n

−n

+ B

†

= n

. (5.7)

Using this, we obtain

−n

)







= (n

 2

−n



)







= 0,

where







= 0 is the eigen ket of n

. Hence, we obtain n



−n



= 0, or



= 0or1. (5.8)

Let us now introduce the relative and net (or CM) momenta (k, q) such that

k ≡

−k

), q ≡ k

; k

= k +

q, k

=−k +

q. (5.9)

We may alternatively represent the pair operators by



≡ c

−k+

≡ B

, B

 †

≡ c

†

−k+



. (5.10)

The prime on B

will be dropped hereafter. From Equation (5.8) we deduce that

the number operator in the k-q representation

≡ B

†

, (5.11)

has eigenvalues 0 or 1:



= 0or1. (5.12)

The total number of a system of pairons, N, is represented by

N ≡



, (5.13)

where

≡



†

(5.14)

represents the number of pairons having net momentum q. From Equations (5.12),

(5.13) and (5.14) we see that the eigenvalues of the number operator n

are non-

negative integers. To explicitly see this property, we introduce

64 5 Quantum Statistics of Composites

≡



(5.15)

and obtain, after using Equations (5.2), (5.3), (5.4), (5.5) and (5.10),

, n

] =



(1 −n

−n

−k+

= B

, [n

, B

†

] = B

†



. (5.16)

Although the occupation number n

is not connected with B

as n

= B

†

,the

eigenvalues n



of n

satisfying Equation (5.16) can be shown straightforwardly to

yield [1]



= 0, 1, 2,.... (5.17)

with the eigenstates



= B

†



= B

†



, ... . (5.18)

This is important. We illustrate it by taking a one-dimensional motion. The pairon

occupation-number states may be represented by drawing quantum cells in the (k, q)

space. From Equation (5.12) the number n



are limited to 0 or 1, see Fig. 5.1. The

number of pairons characterized by the net momentum q only, n



, is the sum of the

numbers of pairs at column q, and clearly it is zero or a positive integer.

In summary, pairons with both k and q speciﬁed are subject to the Pauli ex-

clusion principle, see Equation (5.12). Yet, the occupation numbers n



of pairons

having CM momentum q are0,1, 2,...,see Equation (5.17). Note that our results

Equations (5.8), (5.12) and (5.17) are obtained by using the pair commutators (5.3)

and (5.4). Further note that our result (5.17) does not follow from consideration

of the symmetry of the wavefunction, the symmetry arising from Equation (5.3)

only. Equation (5.4) is needed to prove Equation (5.16). The fact that the quantum

Fig. 5.1 The number

representation of many

electron-pairs in the (k, q)

space

5.2 Two-Particle Composites 65

statistics depend on whether we specify (k, q )orq alone arises because a composite

by construction has more degrees of freedom than an elementary particle (electron).

Only with respect to the CM motion pairons are bosonic and can multiply occupy

the same net momentum state q. We say in short that pairons move as bosons.

(B) Different-fermion composite. The quantum state for two distinguishable

particles (1, 2) can be represented by



(1)

, k

(2)



≡



(1)





(2)



. (5.19)

We may represent the state



( j)



for the particle j by specifying a set of occupa-

tion numbers (n

( j)

, n

( j)

,...) with the restriction that each n

( j)

can take on a value

either 0 or 1, and only one member of the set takes the value 1. These numbers n

( j)

can be represented by [10]

( j)

≡ η

( j)†

( j)

, (5.20)

where creation (annihilation) operators η

( j)†

(η

( j)

) satisfy the Fermi anticommuta-

tion rules (5.2). The quantum state for a many-electron-many-proton system may

be represented by a generalization of Equation (5.19), the direct product of a many-

electron (antisymmetric) state and a many-proton (antisymmetric) state. Such states

can be described in terms of second-quantized operators c



s (electrons) and a



(protons), both satisfying the anticommutation rules (5.2). Following Dirac [1], we

postulate that observables for different particles commute:

(1)

, n

(2)

] = 0, (5.21)

based on which we may choose such that c



s and a



s anticommute with each other

{c, a

†

}={c, a}=0. (5.22)

Pair operators are deﬁned by

†

≡ a

†

, B

≡ c

. (5.23)

We study the number operator n

(H)

deﬁned in the form (5.14) and show by means

of Equation (5.16) that the eigenvalues of n

(H)

are0,1,2,....Thatis,hydrogens H

move as bosons.

boson operators (b



s) satisfying the Bose commutation rules:

, b

†

] ≡ b

†

−b

†

= δ

, [b

, b

] = 0. (5.24)

Fermion and boson operators mutually anticommute, which is in accord with

Equation (5.21). We obtain

66 5 Quantum Statistics of Composites

, B

}≡B

+ B

= 0 (5.25)

, B

†

⎧

⎪

⎨

⎪

⎩

1 +n

−n

if k

= k

, k

= k

†

if k

= k

, k

= k

†

if k

= k

, k

= k

0 otherwise.

(5.26)

We deﬁne n

and B

as in Equations (5.14) and (5.15), use Equation (5.26) and

obtain

, B

] + B



= 0, (5.27)

, B

†

] − B

†

−



†

= 0. (5.28)

The vacuum state,



, satisfying



= b



= 0, (all k) (5.29)

is deﬁned. One-pair states





= 1



is constructed by





= 1



≡



= B

†



, n



. (5.30)

The two states (



) are the only pair-number states at q that can be con-

structed without violating the restriction imposed by Equation (5.28). In fact, apply-

ing Equation (5.28) to



we obtain



, B

†

] − B

†

−



†







†

−2B

†

−



†





= (n

†

−3B

†

)



= 0,

†



= 3B

†



, (5.31)

indicating that no two-pair state can be constructed in a regular manner. That is,



= B

†



. Hence, fermion-boson composites move as fermions.

(D) Identical boson composite. We introduce pair operators:

†

≡ a

†

≡ a

†

, B

≡ a

. (5.32)

We compute commutators among B and B

†

and obtain

5.2 Two-Particle Composites 67

, B

] = 0, (5.33)

, B

†

] =

⎧

⎪

⎨

⎪

⎩

1 +n

if k

= k

, k

= k

, k

= k

, k

= k

2 +4n

if k

= k

, k

= k

, k

= k

, k

= k

†

if k

= k

, k

= k

, k

= k

, k

= k

†

if k

= k

, k

= k

, k

= k

, k

= k

†

if k

= k

, k

= k

, k

= k

, k

= k

†

if k

= k

, k

= k

, k

= k

, k

= k

†

if k

= k

, k

= k

, k

= k

, k

= k

†

if k

= k

, k

= k

, k

= k

, k

= k

0 otherwise.

(5.34)

Consider a pair creation operator

†

≡



k=0



†

+ B

†



, (5.35)

where the prime on the summation means the omission of the zero-k state. Multi-

plying this equation from the left by n

and from the right by

⌽



, we obtain

†

⌽



≡ n

⎛

⎝



k=0



†

+ B

†

⎞

⎠

⌽



⎛

⎝



k=0



†

+2B

†

⎞

⎠

⌽



, (5.36)

which indicates that B

†

⌽



is not the eigenstate of n

. This is signiﬁcant. The state

corresponding to B

†

⌽



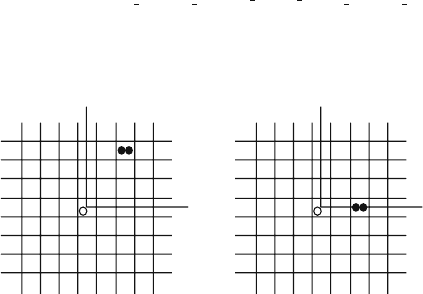
, k = 0 in one dimension is shown in Fig. 5.2 (a). The

corresponding occupation number n

= B

†

has the eigenvalue one since

†

⌽



= a

†

−k+

†

−k+

⌽



= B

†

⌽



, k = 0. (5.37)

(a)

(b)

Fig. 5.2 (a)StateB

†

⌿



, k = 0. (b) State B

†

⌿



68 5 Quantum Statistics of Composites

For k = 0 a straightforward calculation gives

†

⌽



= a

†

⌽



= 2B

†

⌽



. (5.38)

Thus the operator n

has the eigenvalue 2. The state B

†

⌽



is shown in Fig. 5.2

(b). These last two results generate Equation (5.36). In the presence of the double

occupancy at k = 0, we ﬁnd no one-pair number state. This anomaly does not occur

when dealing with elementary fermions since the double occupancy is excluded by

Pauli’s exclusion principle.

5.3 Discussion

In 1940 Pauli established the spin-statistics theorem [2]: half-integral spin elemen-

tary particles are fermions while integral spin particles are bosons. He derived it by

applying general principles of quantum theory and relativity to elementary particles.

Just as elementary particles, composites are experimentally found to be indistin-

guishable and move either as bosons or as fermions (quantum statistical principle).

This can be understood simply if the CM of a composite moves, following the same

general principles, and if the spin-statistics theorem is applied. We take Democritos’

atomistic view: every matter is composed of massive “atoms” (elementary particles).

(Massless quantum particles such as photons and neutrinos will not be considered

hereafter.) We saw in case (D) that no one-pair state for the identical boson pair can

be constructed. Hence, this composite moves neither as a boson nor as a fermion in

violation of the quantum statistical principle. The arguments quoted earlier for the

EOB’s rule fail in this case. Electrons and nucleons have half spins while pions have

zero spin. Hence the other three cases (A)–(C) are in accord with the spin-statistics

theorem and also with the EOB’s rule.

In our derivation we omitted consideration of spin, isospin, ....Wenowdiscuss

this point. Following Dirac [1], we deﬁne the indistinguishability of a system of

identical elementary particles in terms of the permutation symmetry:

[P, H] = [P,ξ] = 0, (all ξ and all P) (5.39)

[P,ρ] = 0, (5.40)

where

H = H(η

,η

,...,η

) (5.41)

is the Hamiltonian of N particle-variables η containing position, momentum and

other quantum variables such as spin, isospin, ...;ξ is a system-dynamical function

such as the center-of mass and the total momentum; P



s are permutation operators

of N particle indices. The density operator ρ is deﬁned in the form:

5.3 Discussion 69

ρ ≡









= 1, (5.42)

where



are symmetric (antisymmetric) kets for bosons (fermions) and P

is the

occupation probability. The particle state is characterized by momentum k, spin-

component σ , isospin-component τ ,....Thestatemayequivalently be represented

by position r, σ , τ,....Thesetofmomenta,{k}, is inﬁnite since the position conju-

gate to the momentum is a continuous variable. Dirac’s relativistic wave equation [1]

indicates that the electron (antiparticle) each has spin 1/2. Pauli’s spin-statistics the-

orem [2] originates in the relativistic quantum motion of the particles in the ordinary

three-dimensional space [2]. In contrast other sets {σ }, {τ }, ...are all ﬁnite, and

hence these variables play secondary roles in quantum statistics. This is so because

the quantum statistics of the particles must be deﬁned with the condition that there

are an inﬁnite set of particle-states. In fact, if there were only one state, neither sym-

metric nor antisymmetric states can be constructed. If there were only two states, no

antisymmetric states for three particles can be constructed. Limiting the number of

particles is unnatural and must be avoided.

We have studied the eigenvalues of the pair-number operators (n

, n

which are observables in Dirac’s sense [1]. All of our results are obtained without

introducing the Hamiltonian. Hence, our results are likely to be valid independently

of any interaction and energy (bound or unbound). This is signiﬁcant, and is sup-

ported by the following arguments. We consider a system of interacting particles

and write the Hamiltonian H in the form

H = H

+λV, (5.43)

where H

is the sum of the single-particle Hamiltonian:



J=1

(η

), (5.44)

V is an interaction Hamiltonian, and λ a coupling constant. For λ = 0 quantum

statistics is postulated. Consider now a continuous limit:

λ → 1. (5.45)

No continuous limit can change discrete (permutation in our case) symmetry.

Hence the quantum statistics arising from the particle-permutation symmetry and

relativistic quantum dynamics is unchanged in the limit (5.45). Such demonstration

can be extended to the case of an interaction Hamiltonian with other particle-ﬁelds.

All experiments appear to support our view: independence of the statistics upon

interaction.

We saw in (A) that the CM motion of a pairon is bosonic while its motion

with both (k, q) speciﬁed is fermionic. This means that the fermionic nature of the

70 5 Quantum Statistics of Composites

constituents (electrons) is important for the total description of a composite (pairon).

This is a general character of any composite. In fact Bardeen, Cooper and Schrieffer,

in their historic paper on superconductivity [9], used the fermionic property (5.3) to

construct the ground-state of a BCS system, the state of the pairons bosonically

condensed all at zero CM momentum. By assuming the spin-statistics theorem for

composites Feynman argued that the pairons move as bosons [10], and proceeded

to derive the Josephson equations [11, 12], which will be discussed later, Chapter

11. Both fermionic and bosonic properties of the pairons must be used in the total

description of superconductivity[13 – 15].

Let us now consider a three-identical fermion composite. Triplet operators (T, T

†

)

are deﬁned by

†

123

≡ c

†

, T

123

= c

. (5.46)

If any two of the momenta (k

, k

) are the same, T ’s vanish due to Pauli’s

exclusion principle. We shall show that the CM motion of the triplet is fermionic.

Decompose the triplet into a system of a two-fermion composite and a fermion.

The CM motion of the pair composite is bosonic according to our study in case (A).

Applying the result in case (C) to the system, we then deduce that the CM motion of

the triplet is fermionic. The above line of argument can be extended to the case of an

N-nucleon system. First, eliminate the multi-occupancy states. Second, split it into

asystemof(N − 1)-nucleon composite and a nucleon. Third, apply the arguments

in either (B)or(C), and deduce that the addition of one nucleon changes quantum

statistics. Next, we consider an atom composed of a nucleus and one electron. By

the same argument the addition of the electron changes quantum statistics. Further

addition of an electron generates the change in statistics.

In summary, the quantum statistics for the CM motion of any composite is deter-

mined by the total number of the constituting elementary fermions. If this number

is odd (even), the composite moves as a fermion (boson). Composites may contain

no massive elementary bosons. The EOB’s rule with respect to the CM motion of

a composite follows directly from the commutation relations (5.3) and (5.4) and

their generalizations. We stress that this rule cannot be derived from the arguments

based on the symmetry of a composite wavefunction equivalent to the symmetry

property of the product of the creation operators alone. The quantum statistics of the

constituent particles must be treated separately. For example, the CM of hydrogen

molecules (2e,2p) move as bosons. But ortho-and para-hydrogens have different

internal structures and behave differently because the quantum statistics of the two

constituting protons play a role [16,17].

Experiments show that photons are bosons. A photon in a vacuum runs with the

light speed and cannot stop. Hence the photon does not have the position variable

as a quantum observable. In this respect, it is essentially different from other ele-

mentary fermions such as the electron and nucleon. Pions (π), and kaons (K )are

experimentally found to be massive bosons. As we saw in Section 5.2, no massive

elementary bosons exist. These π and K must be regarded as composites. Fermi and

Yang [18] regarded π as a composite of nucleon and antinucleon. In the standard

References 71

model π is regarded as a composite of two quarks [19], where a quark is an elemen-

tary fermion. These theoretical approaches are in line with our theory.

In condensed matter physics, many elementary excitations such as phonons,

magnons, plasmons, etc., appear. These particles cannot travel as fast as photons,

and hence they cannot be considered as relativistic quantum particles in principle.

They cannot have non-zero spins. They must therefore be bosons.

References

1. P. A. M. Dirac, Principle of Quantum Mechanics, 4th ed. (Oxford University Press, London,

1958), p. 211, pp. 136–138, p. 37, pp. 253–257.

2. W. Pauli, Phys. Rev. 58, 716 (1940).

3. P. Ehrenfest and J. R. Oppenheimer, Phys. Rev. 37, 331 (1931).

4. H. A. Bethe and R. Jackiw, Intermediate Quantum Mechanics, 2nd ed. (Benjamin, New York,

1968), p. 23.

5. L. N. Cooper, Phys. Rev. 104, 1189 (1956).

6. R. P. Feynman, R. B. Leighton and M. Sands, Feynman Lectures on Physics,Vol.III (Addison-

Wesley, Reading, MA, 1965), pp. 21–28.

7. S. Fujita, Introduction to Non-Equilibrium Quantum Statistical Mechanics (Krieger, Malabar,

FL, 1983), pp. 9–11.

8. S. Fujita and D. L. Morabito, Int. J. Mod. Phys. B 12, 2139 (1998).

9. J. Bardeen, L. N. Cooper and J. R. Schrieffer, Phys. Rev. 108, 1175 (1957).

10. R. P. Feynman, Statistical Mechanics (Addison-Wesley, Redwood City, CA, 1972), p. 304.

11. B. D. Josephson, Phys. Lett. 1, 251 (1992).

12. B. D. Josephson, Rev. Mod. Phys. 36, 216 (1964).

13. S. Fujita and S. Godoy, Quantum Statistical Theory of Superconductivity (Plenum, New York,

1996), pp. 122–124.

14. S. Fujita, J. Supercond. 4, 297 (1991).

15. S. Fujita, J. Supercond. 5, 83 (1992).

16. D. M. Dennison, Proc. Roy. Soc. London 115, 483 (1927).

17. T. Hori, Zeits. f. Physik 44, 834 (1927).

18. E. Fermi and C. N. Ynag, Phys. Rev. 76, 1739 (1949).

19. M. Gell-Mann and Y. Ne’eman, The Eightfold Way (Benjamin, Reading, MA, 1964).

Chapter 6

Quantum Statistical Theory

The pairons move with linear dispersion relations. The 2D system of the pairons

undergoes a Bose–Einstein condensation at the critical temperature T

, k

1.24 v

1/2

, where n is the pairon density and v

the Fermi speed. The super-

conducting transition is a phase change of second order.

6.1 The Full Hamiltonian

Fujita and his group developed a quantum statistical theory of superconductivity in

a series of papers [1–5]. We present this theory in the present chapter.

In the ground state there are no currents for any system. To describe a ring super-

current that can run indeﬁnitely at 0 K, we must introduce moving pairons, that is,

pairons with ﬁnite center-of-mass (CM) momenta. Creation operators for “electron”

(1) and “hole” (2) pairons are deﬁned by

(1)†

≡ B

(1)†

↑k

↓

≡ c

(1)†

, B

(2)†

≡ c

(2)†

. (6.1)

(The pairon operators are denoted by B’s, which should not be confused with the

magnetic ﬁeld B.) We calculate the commutators among B and B

†

, and obtain

(Problem 6.1.1)

( j)

, B

( j)

] = 0, [B

( j)

]

= 0. (6.2)

( j)

, B

( j)†

] =

⎧

⎪

⎨

⎪

⎩

1 −n

( j)

−n

( j)

if k

= k

and k

= k

( j)

( j)†

if k

= k

and k

= k

( j)

( j)†

if k

= k

and k

= k

0 otherwise.

(6.3)

Pairon operators of different types j always commute:

(i)

, B

( j)

] = 0ifi = j (6.4)

S. Fujita et al., Quantum Theory of Conducting Matter,

DOI 10.1007/978-0-387-88211-6



Springer Science+Business Media, LLC 2009

Fujita S., Ito K., Godoy S. Quantum Theory of Conducting Matter - Superconductivity

Подождите немного. Документ загружается.