Финаев В.И. Моделирование при проектировании информационно-управляющих систем
Подождите немного. Документ загружается.


∑
β+β=η
=
5
1i
ii0
x
,
матрица независимых переменных
1,8u ,0,5j ),(XX
u j
===
является
матрицей ортогонального планирования. Оценки неизвестных
коэффициентов функции отклика определятся
.0,4j ,y125,0
8
1u
uu jj
=
∑
=β
=
x
Очевидно, что по сравнению с ПФЭ
2
5
в ДФЭ 2
5-2
число опытов
уменьшено в четыре раза.
Методом математической индукции можно определить, что число
дробных реплик
2
k-g
равно
2
)1q(k
C4
−−
β
=ν ,
где
β
k-(g-1)
- число всех взаимодействий до [k-(g+1)]-гo порядка
включительно, причем
β
k-(g-1)
=2
k-g
-[k-(g-1)].
6.4.2. Выбор дробных реплик.
При выборе функций отклика
предполагалось, что известные коэффициенты при взаимодействиях
факторов равны нулю, что далеко не всегда соответствует реальным
ситуациям. Если применять регулярные реплики, то в этом случае
возможны события, когда число неизвестных параметров функции отклика
будет больше числа опытов
|{Y
u
}|.
В этом случае допускается оценивание коэффициентов при линейных
членах, смешанных со взаимодействиями высших порядков. Может быть
смешанной часть оценок при парных взаимодействиях.
Рассмотрим пример использования реплик для случая, когда число
неизвестных параметров функции отклика больше числа опытов.
Пусть функция отклика имеет вид
η=β
0
+ β
1
x
1
+β
2
x
2
+ β
3
x
3
+ β
12
x
1
x
2
+β
13
x
1
x
3
+ β
23
x
2
x
3
. (6.13)
Имеется дробный факторный план D, задаваемый генерирующим
соотношением х
3
= х
1
х
2
:
4
3
2
1
-13
321
y
y
y
y
1 1 1
1- 1 1-
1- 1- 1
1 1- 1-
D
>−
>−
>−
>−
=
xxx
.
Число неизвестных коэффициентов в функции отклика
p+1=7, число
наблюдений
N
0
=4, N
0
<p+1.
Составим матрицу независимых переменных
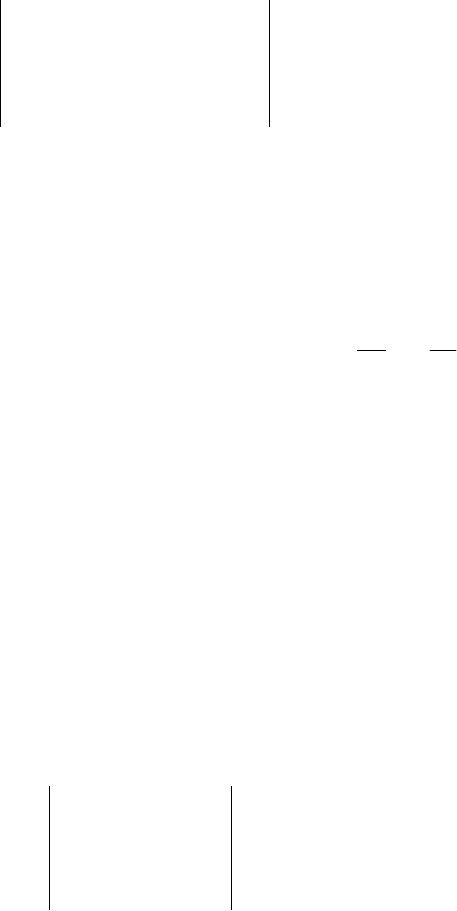
)
u j
X(
ˆ
x
1 1 1
4
x
1 1 1 1
1- 1 1- 1- 1 1- 1
1 1- 1- 1- 1- 1 1
1- 1- 1 1 1- 1- 1
X
3
x
2
x
3
x
1
x
2
x
1
x
3
x
2
x
1
x
0
x
==
44344214434421
Информационная матрица
S=X
T
X будет вырожденной, т. к. она матрица
порядка 7x7, а
rankS=4. Следовательно, уравнение (6.7) будет иметь
бесконечное множество решений.
Для рассмотренного примера модель наблюдений
M{Y}=Xβ,
D{Y}=σ
2
1
I
n0
является моделью наблюдений неполного ранга, поскольку
rankX=N
0
<p+14. Здесь σ
2
- неизвестный параметр, I
n0
- единичная матрица
порядка
N
0
.
Для получения решений сводят задачу исследований модели
наблюдений неполного ранга к задаче исследования модели наблюдений
полного ранга
M{Y}=X
0
β
r
, D{Y}=σ
2
1
I
n
, где X
0
=(X
ij
),
r1,j ,n1,i ==
-
матрица порядка
r; β
r
=β
0
+Aβ*, β
r
=(β
1
,β
2
,…,β
r
)
T
- вектор неизвестных
параметров;
A=(X
0T
X)
-1
X
0T
X*,β
0
=(β
1
,β
2
,…,β
r
)
T
, β*=(β
r+1
,β
r+2
,…,β
p
)
T
,
X=(X
0
,X*).
Свести модель наблюдений неполного ранга к модели наблюдений
полного ранга можно, если допустить смешивание неизвестных параметров
векторов
β
0
и β*.
Как видно из матриц
D
3-1
и X, в точках плана, в которых выполняются
наблюдения
{Y
u
}, имеют место следующие равенства:
x
1
=x
2
x
3
, x
2
=x
1
x
3
, x
3
=x
1
x
2
.
Функцию отклика (6.13) запишем в виде
∑
β+β=η
=
5
1i
ii0
,x (6.14)
β
r
0
=β
0
, β
r
1
=β
1
+β
23
, β
r
2
=β
2
+β
13
, β
r
3
=β
3
+β
12
.
Эта функция отклика будет определена в точках плана D
3-1
, а матрица
X
0
будет иметь вид
)X(
1 1 1 1
1- 1 1- 1
1- 1- 1 1
1 1- 1- 1
X
0
u j
0
3210
==
xxxx
Функция отклика (6.14) соответствует модели наблюдений полного
ранга, которая называется приведенной моделью
M{Y}=X
0
β
r
, D{Y}=σ
2
I
4
, RankX
0
=rankX=4.

Матрица X
0
является матрицей ортогонального планирования U,
следовательно, существуют однозначные оценки вектора
β
r
β
r
=(X
OT
X
O
)
-1
X
OT
Y=(X
OT
Y)/N,
или для каждой
j-той компоненты
∑
==
∑
=β
==
4
1u
u
0
u j0
0
N
1u
u
0
u j
r
j
0,3j ,y25.0N/)y( xx .
Отметим, что
1 1 1
1- 1 1-
1 1- 1-
1- 1- 1
X
*
323121
=
xxxxxx
.
Формально определено, что
β
r
=β
0
+Aβ*, причем β
r
=(β
r
0
,β
r
1
,β
r
2
,β
r
3
)
T
,
β
0
=(β
0
,β
1
,β
2
,β
3
)
T
, β*=(β
12
,β
13
,β
23
)
T
, а матрицу A находим из уравнения
A=(X
0T
X)
-1
X
0T
X* и она имеет вид
0 0 1
0 1 0
1 0 0
0 0 0
A =
.
Если решить при этих условиях уравнение
β
r
=β
0
+Aβ*, то получим
систему параметрических функций
β
r
0
=β
0
, β
r
1
=β
1
+ β
23
, β
r
2
= β
2
+β
13
, β
r
3
=β
3
+ β
12
.
Для получения правила смешивания, с помощью которого можно было
определить, совокупность каких линейных эффектов и эффектов
взаимодействия оценивается, введено понятие контраста плана или
определяющего контраста. Правила смешивания с помощью
определяющего контраста отображаются в системе линейно независимых
параметрических функций, допускающих посмещенное оценивание.
Определяющим контрастом полуреплики 2
k-1
называют ее
генерирующее соотношение, умноженное на свою левую часть [13].
Если генерирующее соотношение полуреплик
2
k-1
задано соотношением
m
i
3
i
2
i
1
ik
. . . xxxxx = , где 1<i
1
<i
2
<…<i
m
<k-1, 1<m<k-2, то, умножив
его на
x
k
, получим
k
m
i
2
i
1
i
2
k
. . . xxxxx = .
Так как
x
k
∈[-1,+1], то определяющий контраст имеет вид
k
m
i
2
i
1
i
. . . 1 xxxx
=
.

Умножая данные уравнения последовательно на переменные
)k1,i ( ,
i
=x , получим систему равенств, на базе которой составляется
система параметрических функций.
Например, для дробной реплики
2
3-1
, задаваемой генерирующим
соотношением х
3
=х
1
х
2
, определяющий контраст имеет вид 1=x
1
x
2
x
3
.
Умножим его на переменные х
1
, х
2
и х
3
и получим систему равенств:
3232
2
11
xxxxxx ==
,
313
2
212
xxxxxx ==
,
21
2
3213
xxxxxx ==
.
Эта система равенств устанавливает соответствие для составления системы
параметрических функций
β
r
1
=β
1
+ β
23
<===> x
1
=x
2
x
3
;
β
r
2
= β
2
+β
13
<===> x
2
=x
1
x
3
;
β
r
3
=β
3
+ β
12
<===> x
3
=x
1
x
2
.
Но данный подход не позволяет получить несмещенные (раздельные)
оценки параметров
β
1
, β
2
, β
3
. Чтобы решить эту задачу, достаточно
построить еще полуреплику
2
3-1
, которая будет задаваться генерирующим
соотношением х
2
=-х
1
х
3
. Система равенств, отображающих смешивание,
будет иметь вид x
1
=-x
2
x
3
; x
2
=-x
1
x
3
; x
3
=-x
1
x
2
.
Следовательно, возможно МНК - оценка следующих неизвестных
коэффициентов:
β
r*
1
=β
1
+β
23
, β
r*
2
=β
2
+β
13
, β
r*
3
=β
3
+β
12
.
На основе оценок полуреплик 2
3-1
(х
4
=х
1
x
3
) и 2
3-1
(х
4
=-х
1
x
3
) находим
несмещенные оценки
1,3i ),
*r
i
β
i
β(5.0
i
β =+= .
Рассмотрим аналогичную задачу нахождения смещенных оценок для
полуреплики
2
4-1
. Пусть функция отклика имеет вид
.
43214 3 2 1
4lji1
ljil j i
4ji1
jij i
4i1
ii0
xxxxxxxxxx
β
+
∑
β+
∑
β
+
∑
β+β=η
<<<<<<<<<
Матрица плана ДФЭ 2
4-1
построена с использованием генерирующего
соотношения х
4
=х
1
х
2
. Определяющий контраст имеет вид 1=x
1
x
2
x
4
.
Умножим его последовательно на переменные х
1
, х
2
, х
3
, х
4
. Получим
следующую систему равенств:
1=x
1
x
2
x
4
; x
1
=x
2
x
4
; x
2
=x
1
x
4
; x
3
=x
1
x
2
x
3
x
4
; x
4
=x
1
x
2
; x
1
x
3
=x
2
x
3
x
4
;
x
2
x
3
=x
1
x
3
x
4
; x
3
x
4
=x
1
x
2
x
3
.
Исходя из этой системы равенств, построим систему параметрических
функций, допускающих несмещенное оценивание параметров функции
отклика
β
r
0
=β
0
+β
124
, β
r
1
=β
1
+ β
12
, β
r
2
= β
2
+β
14
, β
r
3
=β
3
+ β
1234
.
β
r
4
=β
4
+ β
12
, β
r
5
= β
13
+β
234
, β
r
6
=β
23
+ β
134
, β
r
7
=β
34
+ β
123
.
Если для оценивания параметров функции отклика применяется (1/4)-
реплика или реплики более высокой дробности, то система смешивания

линейных эффектов и эффектов взаимодействий между собой будет более
сложной, поскольку для задания
(1/g)-реплик (g>2) необходимо не менее
двух генерирующих соотношений.
Пусть четверть-реплика
2
5-2
задается генерирующими соотношениями
x
4
=x
1
x
2
и x
5
=x
1
x
2
x
3
. Умножив их на x
4
и x
5
соответственно, получим
определяющие контрасты
1=x
1
x
2
x
4
; 1=x
1
x
2
x
3
x
5
.
Если их перемножим, то получим еще один определяющий контраст
1=x
3
x
4
x
5
. Затем получаем обобщенный определяющий контраст
1=x
1
x
2
x
4
=x
1
x
2
x
3
x
5
=x
3
x
4
x
5
.
Для получения системы равенств, отображающих систему смешивания
независимых переменных и взаимодействий, следует умножать
отображенный определяющий контраст последовательно на независимые
переменные x
1
, x
2
, x
3
, x
4
, x
5
. Система уравнений будет иметь следующий
вид:
x
1
=x
2
x
4
=x
2
x
3
x
5
=x
1
x
3
x
4
x
5
;
x
2
=x
1
x
4
=x
1
x
3
x
5
=x
2
x
3
x
4
x
5
;
x
3
=x
1
x
2
x
3
x
4
=x
1
x
2
x
5
=x
4
x
5
;
x
4
=x
1
x
2
=x
1
x
2
x
3
x
4
x
5
=x
3
x
5
;
x
5
=x
1
x
2
x
4
x
5
=x
1
x
2
x
3
=x
3
x
4
;
x
1
x
3
=x
2
x
4
x
3
=x
2
x
5
=x
1
x
4
x
5
;
x
1
x
5
=x
2
x
4
x
5
=x
2
x
3
=x
1
x
3
x
4
.
С учетом обобщенного определяющего контраста получено восемь
равенств, которые однозначно определяют систему параметрических
функций смешивания эффектов:
β
r
0
=β
0
+ β
124
+ β
335
+ β
1235
; β
r
1
=β
1
+ β
24
+ β
235
+ β
1345
;
β
r
2
=β
2
+ β
14
+ β
135
+ β
2345
; β
r
3
=β
3
+ β
45
+ β
125
+ β
1234
;
β
r
4
=β
4
+ β
12
+ β
35
+ β
12345
; β
r
5
=β
5
+ β
34
+ β
123
+ β
1245
;
β
r
6
=β
13
+ β
25
+ β
145
+ β
234
; β
r
7
=β
15
+ β
13
+ β
134
+ β
245
.
Получен вектор
),...,(
r
7
r
2
r
1
r
βββ=β
, оценивание которого возможно по
данным вектора наблюдений
Y=(y
1
,y
2
,…,y
8
)
T
и данным матрицы X
0
1 1 1 1 1 1 1 1
1 1 1- 1- 1 1 1- 1
1- 1- 1 1- 1 1- 1 1
1- 1- 1- 1 1 1- 1- 1
1 1- 1- 1 1- 1 1 1
1- 1- 1 1- 1- 1 1- 1
1 1 1- 1- 1- 1- 1 1
1- 1 1 1 1- 1- 1- 1
0
X =
,
которая является матрицей ортогонального планирования и ее
rankX
0
=8.
Проблема выбора дробных планов является основной при
планировании факторных экспериментов. Ее решение направлено на
нахождение таких дробных реплик
2
k-g
, которые бы позволили получить
несмещенные МНК-оценки для всех неизвестных параметров функции
отклика. Отметим особенности применения дробных реплик:
- число опытов
N
0
<p+1 - числа неизвестных параметров модели;
- модель наблюдений является моделью неполного ранга, равного
N
0
;
- матрица независимых переменных приведенной модели полного ранга
является матрицей ортогонального планирования;
- система параметрических функций, допускающих оценку, выводится
из определяющих контрастов.
6.5. ПОИСК ЭКСТРЕМУМА ФУНКЦИИ ОТКЛИКА
6.5.1. Определение стратегии поиска. Если линейная модель
наблюдений описывает некоторые процессы, то ставится задача
нахождения набора входных параметров, при которых выходной параметр
будет экстремальным либо будет находиться в определенной области
значений. Например, линейная модель описывает технологический процесс
и необходимо определить набор условий (входных факторов), при которых
производительность процесса будет максимальной, либо набор условий,
при
которых выход бракованных изделий сведен к минимуму. Формально
задача сводится к отысканию вектора
Х=(х
1
,x
2
,...,х
k
)∈G при условии
).x , . . . ,x ,f(x max}x , . . . ,x ,M{y/x
k21
Gx
k21
∈
=
Для нахождения экстремума функции отклика необходимо исследовать
поверхность отклика посредством проведения изменений поверхности в
различных точках факторного пространства.
Стратегия поиска состоит в том, чтобы число измерений (опытов) было
сведено к минимальному значению, т. к. каждый опыт - это эксперимент на
функционирующем объекте.
Наибольшее распространение получили градиентные методы поиска
экстремума, при которых
движение по поверхности отклика происходит в
направлении оценки градиента. Оценка градиента
gradf(x
1
,x
2
,...,x
k
) в точке
(x
1
,x
2
,...,x
k
) происходит по результатам измерений, проводимым в
окрестностях этой точки в факторном пространстве.
Бокс и Уильсон [15, с. 410] предложили использовать
последовательный «шаговый» метод изучения поверхности отклика. При
этом ставится небольшая серия опытов для локального описания
поверхности отклика полиномом первой степени. Далее движение
осуществляется по поверхности отклика в направлении градиента
линейного приближения. Если
одного линейного приближения достаточно,
то ставится новая небольшая серия опытов и находится новое направление
движения по поверхности отклика. Такой процесс движения продолжается,
пока исследователь не попадет в почти стационарную область, где
линейное приближение оказывается недостаточным. В этой области

ставится большая серия опытов и поверхность отклика описывается
полиномом второго и третьего порядка.
Метод Бокса и Уильсона состоит в повторении процедуры:
- построение факторного эксперимента в окрестности некоторой точки;
- вычисление оценки градиента в этой точке по результатам
эксперимента;
- крутое восхождение в направлении оценки градиента;
- нахождение оценки экстремального значения функции отклика
по
этому направлению.
6.5.2. Метод крутого восхождения. Метод крутого восхождения
предполагает, что функция отклик
а η=f(x
1
,x
2
,...,x
k
) непрерывна, имеет
непрерывные частные производные первого порядка на множестве
G∈R -
k-мерному евклидову пространству и унимодальна, т.е. в области G имеет
единственный экстремум.
Основу метода отыскания экстремума функции
η=f(x
1
,x
2
,...,x
k
)
составляет метод подъема (или спуска) по поверхности функции
η. При
этом находится последовательность точек
X
0
,X
1
,...,Х
m
в области G, таких,
что
f(X
0
)>f(X
1
)>...>f(X
m
)>... (или f(X
0
)<f(X
1
)<...<f(X
m
)<... ).
Градиентным называется метод, согласно которому точка
Х
m+1
выбирается из условия [13]
Х
m+1
=Х
m
+αgradf(Х
m
), где
T
m
k
x
f
, . . . ,
m
2
x
f
,
m
1
x
f
)
m
f(X )
m
f(X grad
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
∂
∂
∂
∂
∂
∂
=∇=
∑
- вектор-градиент функции
f(x
1
,x
2
,...,х
k
) в точке
)x , . . . ,x ,(xX
m
k
m
2
m
1
1m
=
+
;
α - некоторая скалярная величина, α > 0.
Различие градиентных методов состоит в разных методиках выбора
величин
α. Рассмотрим суть крутого восхождения (спуска), иллюстрация
которого приведена на рис.6.4. На этом рисунке при
К=2, задавая
различные значения
С из уравнения f(x
1
,x
2
)=C, получены совокупности
линий уровня.
Пусть
X
0
- начальная точка при поиске максимума функции отклика
η=f(x
1
,x
2
,...,х
k
). Вектор-градиент ∇η в точке Х
0
определится
T
0
k
0
2
0
1
0
k
0
2
0
1
x
f
, . . . ,
x
f
,
x
f
)x , . . . ,x ,f(x grad
⎥
⎦
⎤
⎢
⎣
⎡
∂
∂
∂
∂
∂
∂
=
,
где
k1,i ,
x
)x , . . . ,x ,f(x
x
f
0
i
0
k
0
2
0
1
0
i
=
∂
∂
=
∂
∂
.
При условии, что все частные производные не равны нулю (точка
X не
является стационарной), направление вектор-градиента в этой точке будет
направлением наибыстрейшего возрастания функции.
Затем делается шаг в направлении градиента с целью поиска точки X
1
, в
которой значение функции будет наибольшим.
x
1
x
2
X
3
X
2
X
1
X
0
Рис. 6.4
Новая точка
X
1
определяется из решения уравнения при
предположении, что функция унимодальна в направлении градиента
k1,i ,
0
i
x
f
0
α
i
x
1
i
x ),
0
f(X grad
0
α
0
X
1
X =
∂
∂
+=+=
.
В точке
X
1
функция f(X
1
) будет максимальна в направлении градиента
из точки
Х
0
, т. е.
=ααα= ))(x , . . . ),(x ),((x f)x , . . . ,x ,(x f
0
0
k0
0
20
0
1
1
k
1
2
1
1
))(x , . . . ),(x ),((x f max
0
k
0
2
0
1
ααα=
α
.
Затем вычисляется
grad f(X
1
) и делается шаг в его направлении по
поверхности
f(X) с целью поиска точки X
2
и т. д.
В общем случае при наискорейшем подъеме координаты очередной
точки
X
m+1
находят при решении уравнений
=ααα=
+++
))(x , . . . ),(x ),((x f)x , . . . ,x ,(x f
m
m
km
m
2m
m
1
1m
k
1m
2
1m
1
)),(x , . . . ),(x ),((x f max
m
k
m
2
m
1
ααα=
α
причем,
0
i
x
f
m
α
m
i
x)
m
α(
m
i
x)α(
1m
i
x
∂
∂
+==
+
.
В векторной форме
Х
m+1
=Х
m
+α
m
gradf(Х
m
).
Так как
f(X
m+1
)>f(X
m
), то последовательность {Х
m
} сходится к точке
максимума функции отклика.
Параметр α
m
(m=1,2,…) находится из решения одномерной задачи
максимизации [15]
0α ], )
m
f(X gradα
m
[X f
α
max >+ .
6.5.3. Метод Бокса и Уильсона. Выше было отмечено, что движение
по поверхности отклика осуществляется в направлении оценки градиента
функции отклика. Рассмотрим нахождение оценки градиента.
Пусть в области определения
G ∈ R задана функции отклика
η=f(x
1
,x
2
,...,x
k
).
Пусть
X
0
(см. рис.6.4) − произвольно выбранная начальная точка.
Используя ее как центр плана, построим ПФЭ или ДФЭ в окрестностях
этой точки
)x , . . . ,x ,(xX
0
k
0
2
0
1
0
=
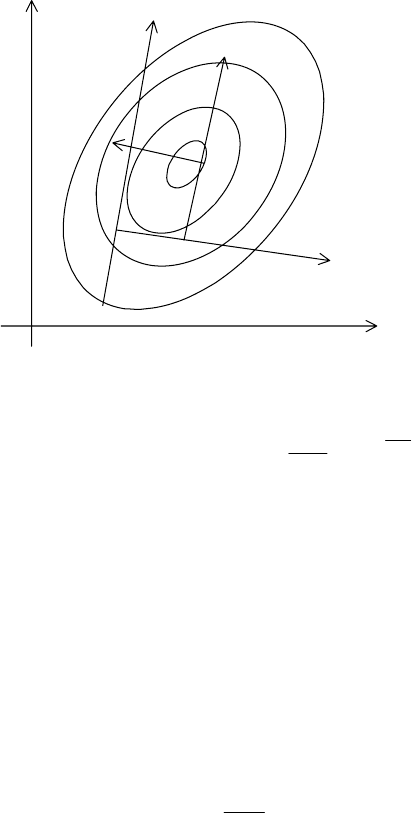
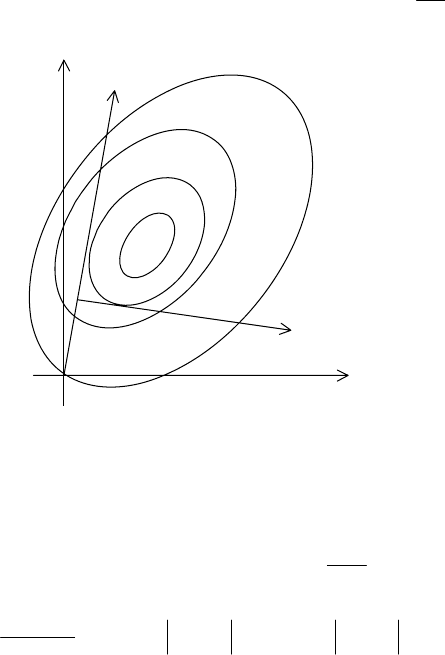
. Как показано на рис.6.5, для примера
введем кодированные переменные
k1,i ,S/)x-x(
0
i
0
iii
==x
, через
которые выразим функцию отклика
η=f(x
1
,x
2
,...,x
k
).
x
1
x
2
X
1
X
0
Рис. 6.5
Как видно из рис.6.5, переход к кодированным переменным означает
перенос начала координат и растяжение (сжатие) по координатным осям
функции отклика.
Разложим функцию
η в точке
) , . . . , ,(
0
k
0
2
0
1
xxx
в ряд Тейлора:
.0)(0lim ),(0
f
5,0
f
),...,,f(),...,,f(η
0
0
k
1i
k
1j
0
ji
0
j
0
i
2
k
1i
i
0
i
0
k
0
2
0
1k21
=
∑∑
+
∂∂
∂
+
∑
∂
∂
+==
→
==
=
x-xx-xxx
xx
x
x
xxxxxx
xx
Введем обозначения

) , . . . , ,( f
0
k
0
2
0
1
0
xxx=β
;
0
i
0
i
f
x∂
∂
=β
;
20
i
2
0
i i
) (
f
x∂
∂
=β
;
.
f
0
j
0
i
2
0
j i
xx ∂∂
∂
=β
После этого функция отклика примет вид
.)()x(f
ki1
2
i
0
i i
kji1
ji
0
j i
ki1
i
0
i
0
0
∑
β+
∑
β+
∑
β+β=η=
<<<<<<<
xxxx
Т.к. градиент функции отклика
gradf(x
0
)=(β
1
,β
2
,...,β
k
), то оценивание
градиента сводится к нахождению МНК - оценок неизвестных параметров
β
1
,β
2
,...,β
k
.
Для простоты предполагают, что функция отклика достаточно точно
аппроксимируется гиперплоскостью
.
k
1i
i
0
i
0
0
∑
β+β=η
=
x
Тогда при выбранном плане
N1,u ,k,1i ),
u i
(XD ===
, МНК – оценки
определяются
.k0,j ,
N
1u
u
Y
u j
XN/1
0
j
β
ˆ
=
=
=
∑
Таким образом, найдена оценка градиента функций
η
в точке
0
x
:
.
T
)
k
β
ˆ
, . . . ,
2
β
ˆ
,
1
β
ˆ
()
0
x f(
ˆ
)
0
k
x , . . . ,
0
2
x ,
0
1
(x f da
ˆ
gr =∇=
Метод Бокса и Уильсона позволяет отыскивать максимум функции
отклика при предположении ее строгой унимодальности в области
определения G.
После того, как была выбрана начальная точка, введено кодирование
переменных и осуществлена оценка градиента функции
η в точке
) , . . . , ,(
0
k
0
2
0
1
xxx
, для поиска максимума делается шаг из точки X
0
в
направлении
)
0
x f( da
ˆ
gr
,)f(X gradXX
01
0
01
0
01
0
βα=α+=
где
0
1
0
>α
-
параметр шага,
T0
k
0
2
0
1
) , . . . , ,( βββ=β
,
.) , . . . , ,(X
T10
k
10
2
10
1
1
xxx=
Каждая компонента точки
X
1
находится из формулы
k.1,i ,
0
i
1
0
10
i
=βα=x
От кодированных переменных осуществляется переход к натуральным
переменным, причем координаты точки
1
0
X
определяются
.S
1
0
10
i
0
i
10
i
xxx +=
Затем в точке
1
0
X
производится ряд измерений функции η и по
наблюдениям (измерениям)
10
k
10
2
10
1
y , . . . ,y ,y
находится оценка
