Федосеев В.В. и др. Экономико-математические методы и прикладные модели

Подождите немного. Документ загружается.

Основы,

линейного программирования

мерного пространства, называемую многогранником реше-

ний, так как координаты каждой его точки являются реше-

нием.

Таким образом, геометрически ЗЛП (2.19)-(2.20) пред-

ставляет собой поиск такой точки многогранника решений,

координаты которой доставляют линейной функции наи-

большее (наименьшее) значение, причем допустимыми ре-

шениями являются все точки многогранника решений.

Если в ЗЛП ограничения заданы в виде неравенств с дву-

мя переменными, она может быть решена графически. Гра-

фический метод решения ЗЛП состоит из следующих этапов.

Этап 1. Сначала на координатной плоскости Х\0х2 стро-

ится допустимая многоугольная область (область допусти-

мых решений, область определения), соответствующая огра-

ничениям. Далее строится вектор-градиент линейной функ-

ции f(X) в какой-нибудь точке x

, принадлежащей допус-

тимой области:

v-(M--

JL-c)

- Т -

l> T

2 •

дх

)

Этап 2. Прямая

СхХ\+С2Х2=

f(x

перпендикулярная век-

тору-градиенту, передвигается в направлении этого вектора

в случае максимизации f(X) до тех пор, пока не покинет

пределов многоугольной области. Предельная точка (или

точки) области при этом движении и является точкой мак-

симума f(X).

Этап 3. Для нахождения координат точки максимума

достаточно решить два уравнения прямых, получаемых из

соответствующих ограничений и дающих в пересечении

точку максимума. Значение f(X), найденное в получаемой

точке, является максимальным.

В случае минимизации f(X) прямую с^ + с^х^ = f(x

)

надо двигать в направлении, противоположном вектору-гра-

диенту. Ясно, что если прямая при своем движении не по-

кидает допустимой области, то соответствующий максимум

или минимум f(X) не существует.

Глава 2

к. Пример 6. Решить графическим методом следующую ЗЛП:

max/(X)= 30JC! + 60х

X! + Ъх

< 21

3*!

+ 2х

< 21

Зх

+ х

*1.2 * 0.

Прямые ограничения означают, что область решений будет

лежать в первой четверти декартовой системы координат;

отметим штриховкой эту область на рис. 2.4.

Этап 1. Определим множество решений первого нера-

венства. Оно состоит из решения уравнения и строгого не-

равенства. Решением уравнения служат точки прямой

х\

+ 3^2

21=0. Построим прямую по двум точкам (0; 7) и

(21;

0), которые легко получить в результате последователь-

ного обнуления одной из переменных. На рисунке обозначим

ее цифрой I.

Множество решений строгого неравенства — одна из по-

луплоскостей, на которую делит плоскость построенная пря-

мая. Какая из них является искомой, можно выяснить при

помощи одной контрольной точки. Если в произвольно взя-

той точке, не принадлежащей прямой, неравенство выпол-

няется, то оно выполняется и во всех точках той полуплос-

кости, которой принадлежит контрольная точка, и не вы-

полняется во всех точках другой полуплоскости. В качестве

такой точки удобно брать начало координат. Подставим ко-

ординаты (0; 0) в неравенство, получим -21 < 0, т.е. оно вы-

полняется. Следовательно, областью решения неравенства

служит нижняя полуплоскость.

Аналогичным образом построим области решения двух

других неравенств

3*!

+ 2х

- 21 = 0; *! = 0, х

= 10,5;

= 0, х

= 7.

(на рисунке прямая II);

Зх\ + 2х

- 21 < 0 при xi = х

= 0, - 21 < 0 выпол-

няется, берется нижняя полуплоскость.

Основы линейного программирования

3*!

+ х

- 18 = 0; х

= 0, х

= 18;

= О, х

= 6.

(на рисунке прямая III);

Ъх\ + #2

18 < 0 при #i = х

= О, - 18 < 0 выполняется,

берется нижняя полуплоскость.

Заштрихуем общую область для всех неравенств, обозна-

чим вершины многоугольника латинскими буквами и опре-

делим их координаты, решая систему уравнений двух пере-

секающихся соответствующих прямых. Например, опреде-

лим координаты точки С, являющейся точкой пересечения

второй и третьей прямой:

3xj + 2х

= 21, х

= 3, х

3*!

+ х

= 18.

Вычислим значение целевой функции в этой точке:

/(X)=30x! + 60х

= 150 + 180 = 330.

Аналогично поступим для других точек, являющихся вер-

шинами замкнутого выпуклого многоугольника OABCD,

представляющего собой область допустимых решений рассмат-

риваемой ЗЛП. Координаты этих вершин имеют следующие

значения: т. О(0;0), т. А(0;7), т. Б(3;6), т. С(5;3), т. D(6;0).

Этап 2. Приравняем целевую функцию постоянной ве-

личине а: 30*1 + 60^2

= а

Это уравнение является множеством точек, в котором

целевая функция принимает значение, равное а. Меняя зна-

чение а, получим семейство параллельных прямых, каждая

из которых называется линией уровня. Пусть а=0, вычис-

лим координаты двух точек, удовлетворяющих соответст-

вующему уравнению 30*i + 60*2 = 0. В качестве одной из

этих точек удобно взять точку О(0;0), а так как при Xi=2

JC2=-1,

то в качестве второй точки возьмем точку G(2;-l).

Через эти две точки проведем линию уровня f(X) = 30*1 +

+ 60^2

0 (пунктирная прямая на рис. 2.4).

Глава 2

i-V4ll);20)

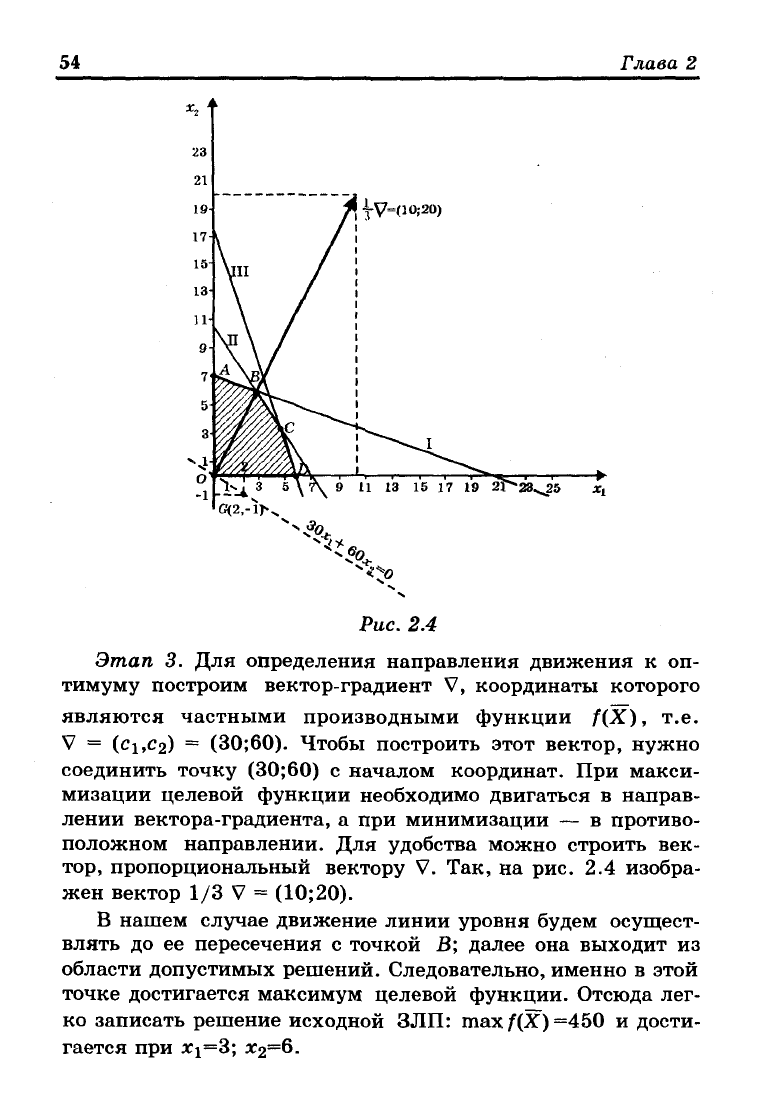
Рис. 2.4

Этап 3. Для определения направления движения к оп-

тимуму построим вектор-градиент V, координаты которого

являются частными производными функции f(X), т.е.

V = (с\,С2) = (30;60). Чтобы построить этот вектор, нужно

соединить точку (30;60) с началом координат. При макси-

мизации целевой функции необходимо двигаться в направ-

лении вектора-градиента, а при минимизации — в противо-

положном направлении. Для удобства можно строить век-

тор,

пропорциональный вектору V. Так, на рис. 2.4 изобра-

жен вектор 1/3 V = (10;20).

В нашем случае движение линии уровня будем осущест-

влять до ее пересечения с точкой В; далее она выходит из

области допустимых решений. Следовательно, именно в этой

точке достигается максимум целевой функции. Отсюда лег-

ко записать решение исходной ЗЛП: max/(X) =450 и дости-

гается при

*i=3;

ДС2=6.

Основы линейного программирования

Если поставить задачу минимизации функции f(X) =

= 30^1 + 60лг2 при тех же ограничениях, линию уровня не-

обходимо смещать параллельно самой себе в направлении,

противоположном вектору-градиенту V. Как это видно на

рис.

2.4, минимум целевой функции достигается в точке

О(0;0),

следовательно, можно записать min/(X)= 0 и дости-

гается при, xi= 0; Х2~ 0. Л

При решении некоторых ЗЛП графическим методом мо-

жет встретиться случай, когда линия уровня параллельна

одной из сторон выпуклого многоугольника допустимых

решений, причем эта сторона расположена в направлении

смещения линии уровня при стремлении целевой функции

к своему оптимуму. В этом случае оптимальное значение

целевой функции достигается не в одной, а в двух угловых

точках (вершинах) многоугольника решений и, следовательно,

во всех точках отрезка, соединяющего эти вершины, т. е.

задача будет иметь бесчисленное множество решений.

Если область допустимых решений является незамкнутым

выпуклым многоугольником в направлении оптимизации

целевой функции, то целевая функция будет неограниченной

и ЗЛП не будет иметь решений; в этом случае условно можно

записать, что, например, max f(X) =

+oo

Очевидно также, что ЗЛП не будет иметь решений в случае,

когда область допустимых решений есть пустое множество,

т. е. система ограничений ЗЛП содержит противоречивые

неравенства, и на координатной плоскости нет ни одной

точки, удовлетворяющей этим ограничениям.

2.5. Симплексный метод решения задачи

Среди универсальных методов решения задач линейного

программирования наиболее распространен симплексный

метод (или симплекс-метод), разработанный американским

ученым Дж. Данцигом. Суть этого метода заключается в

том, что вначале получают допустимый вариант, удовлетво-

ряющий всем ограничениям, но необязательно оптимальный

(так называемое начальное опорное решение); оптимальность

Глава 2

достигается последовательным улучшением исходного

варианта за определенное число этапов (итераций). Нахож-

дение начального опорного решения и переход к следующему

опорному решению проводятся на основе применения рас-

смотренного выше метода Жордана-Гаусса для системы

линейных уравнений в канонической форме, в которой

должна быть предварительно записана исходная ЗЛП; на-

правление перехода от одного опорного решения к другому

выбирается при этом на основе критерия оптимальности

(целевой функции) исходной задачи. Симплекс-метод осно-

ван на следующих свойствах ЗЛП:

Не существует локального экстремума, отличного от

глобального. Другими словами, если экстремум есть, то

он единственный.

Множество всех планов задачи линейного программиро-

вания выпукло.

Целевая функция ЗЛП достигает своего максимального

(минимального) значения в угловой точке многогранни-

ка решений (в его вершине). Если целевая функция

принимает свое оптимальное значение более чем в од-

ной угловой точке, то она достигает того же значения в

любой точке, являющейся выпуклой линейной комби-

нацией этих точек.

Каждой угловой точке многогранника решений отвечает

опорный план ЗЛП.

Рассмотрим две разновидности симплексного метода:

симплекс-метод с естественным базисом и симплекс-метод с

искусственным базисом (или М-метод).

Симплекс-метод с естественным базисом. Для примене-

ния этого метода ЗЛП должна быть сформулирована в кано-

нической форме (2.12) - (2.14), причем матрица системы

уравнений должна содержать единичную подматрицу раз-

мерностью т х т. В этом случае очевиден начальный опор-

ный план (неотрицательное базисное решение).

Для определенности предположим, что первые т век-

торов матрицы системы составляют единичную матрицу.

Тогда очевиден первоначальный опорный план: (Ъ\,Ъ2,...,

,0,...,0).

Основы линейного программирования 57

Проверка на оптимальность опорного плана проходит с

помощью критерия оптимальности, переход к другому опор-

ному плану — с помощью преобразований Жордана-Гаусса

и с использованием критерия оптимальности.

Полученный опорный план снова проверяется на опти-

мальность и т. д. Процесс заканчивается за конечное число

шагов, причем на последнем шаге либо выявляется нераз-

решимость задачи (конечного оптимума нет), либо получа-

ются оптимальный опорный план и соответствующее ему

оптимальное значение целевой функции.

Признак оптимальности заключается в следующих двух

теоремах.

Теорема 1. Если для некоторого вектора, не входящего в

базис, выполняется условие

А; = Zj - с, < О, где Zj = ^c

aij, j = \,п,

i=l

то можно получить новый опорный план, для которого зна-

чение целевой функции будет больше исходного; при этом

могут быть два случая:

а) если все координаты вектора, подлежащего вводу в

базис, неположительны, то ЗЛП не имеет решения;

б) если имеется хотя бы одна положительная координата

у вектора, подлежащего вводу в базис, то можно получить

новый опорный план.

Теорема 2. Если для всех векторов выполняется условие

Aj = Zj -

> 0, то полученный план является оптимальным.

На основании признака оптимальности в базис вводится

вектор Ak, давший минимальную отрицательную величину

симплекс-разности:

- c

= тЩг

}

- с-).

Чтобы выполнялось условие неотрицательности значений

опорного плана, выводится из базиса вектор А

, который дает

минимальное положительное отношение

Q - min—— = ——; од > 0, i =

т.

Глава 2

Строка А

называется направляющей, столбец А^ и эле-

мент а

ь — направляющими (последний называют также

разрешающим элементом).

Элементы вводимой строки, соответствующей направ-

ляющей строке, в новой симплекс-таблице вычисляются по

формулам

a'rj =—

, i = 1>л,

«rfe

а элементы любой другой г-й строки пересчитываются по

формулам:

гк ~

rj '

1к . .

а!, = — , / = 1,т; j = 1,я.

Значения базисных переменных нового опорного плана

(показатели графы «план») рассчитываются по формулам:

Ь'

= А_ для i = г; ь\ =

Лгк

Ъг

'*, t

T^i для i * г.

гк

Если наименьшее значение Q достигается для несколь-

ких базисных векторов, "то чтобы исключить возможность

зацикливания (повторения базиса), можно применить сле-

дующий способ.

Вычисляются частные, полученные от деления всех эле-

ментов строк, давших одинаковое минимальное значение Q,

на свои направляющие элементы. Полученные частные со-

поставляются по столбцам слева направо, при этом учиты-

ваются и нулевые, и отрицательные значения. В процессе

просмотра отбрасываются строки, в которых имеются боль-

шие отношения, и из базиса выводится вектор, соответст-

вующий строке, в которой раньше обнаружится меньшее

частное.

Для использования приведенной выше процедуры сим-

плекс-метода к минимизации линейной формы /(X) следует

искать максимум функции Д(Х) =

-f(X),

затем получен-

ный максимум взять с противоположным знаком. Это и бу-

дет искомый минимум исходной ЗЛП.

Основы линейного программирования

Рассмотрим алгоритмы симплекс-метода на конкретной

задаче.

Пример 7. Для производства продукции типа П\ и

11%

предприятие использует два вида сырья: С\ и С

- Данные об

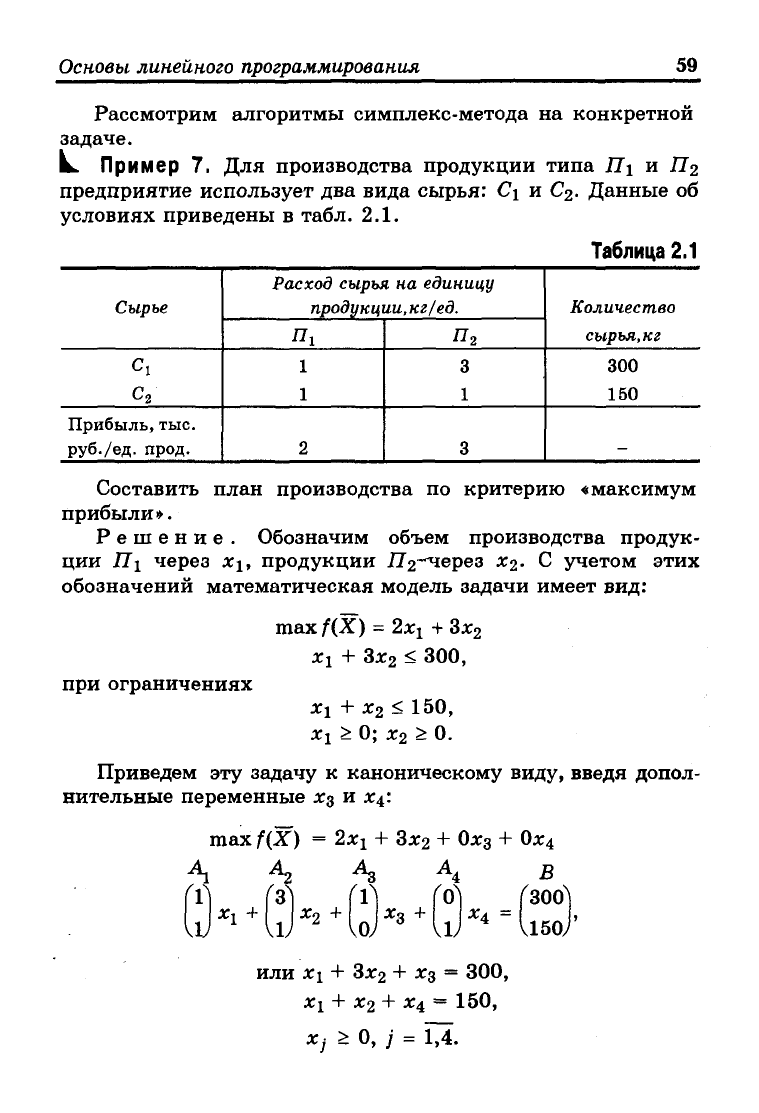
условиях приведены в табл. 2.1.

Таблица

2.1

Сырье

Прибыль, тыс.

руб./ед. прод.

Расход сырья на единицу

продукции,

кг/ед.

Количество

сырья,

кг

300

150

Составить план производства по критерию «максимум

прибыли».

Решение. Обозначим объем производства продук-

ции iTi через х\, продукции Л^-через х

. С учетом этих

обозначений математическая модель задачи имеет вид:

гаах/(Х) = 1х

+ 3*2

xi + Зх

^ 300,

при ограничениях

Х\ + х

< 150,

X! > 0; х

> 0.

Приведем эту задачу к каноническому виду, введя допол-

нительные переменные хз и х

m&xf(X) = 2x

+ Zx

Л,

'if

Л,

Охз + 0х

Гзоо

~ VI50,

или xi + 3x2 + #3

300,

Xj + Х2 + Х

= 150,

> 0, j = 1

,4.

60 Глава 2

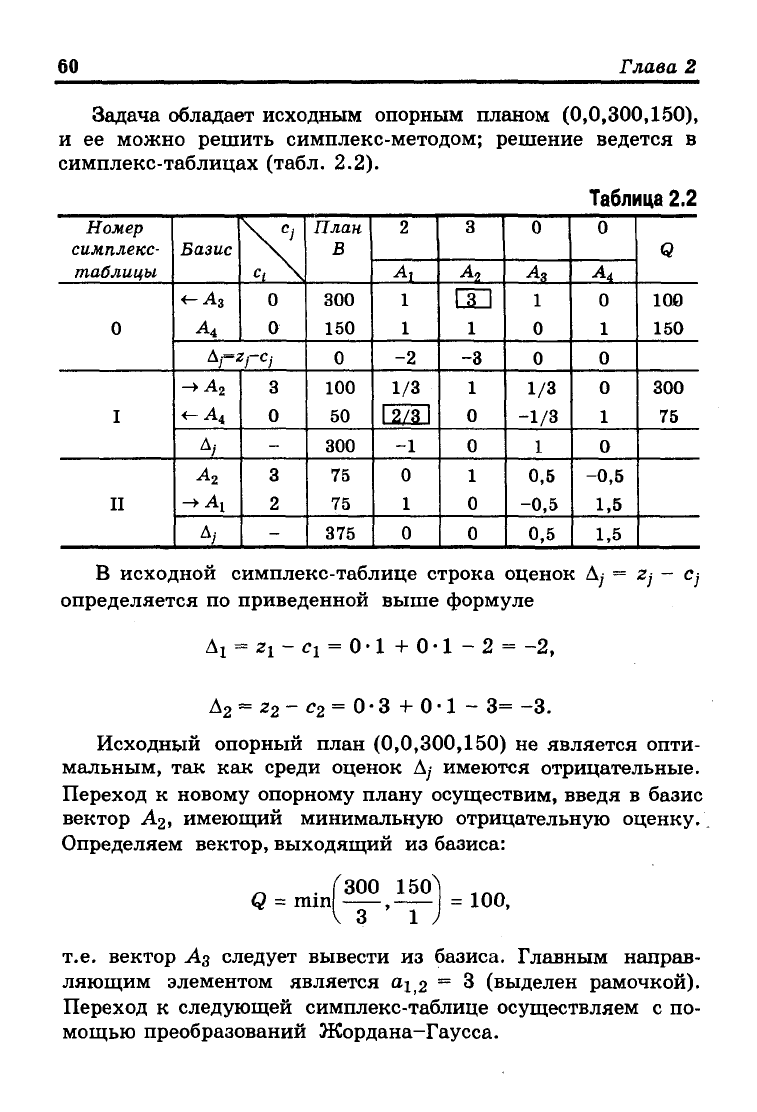
Задача обладает исходным опорным планом (0,0,300,150),

и ее можно решить симплекс-методом; решение ведется в

симплекс-таблицах (табл. 2.2).

Таблица 2.2

Номер

симплекс-

таблицы

Базис

<-А

;

->А

<- А

;

План

300

150

100

300

375

-2

1/3

12/81

-1

СО

-3

1/3

-1/3

0,5

-0,5

0,5

-0,5

1,5

100

150

300

В исходной симплекс-таблице строка оценок Aj = Zj - Cj

определяется по приведенной выше формуле

Ai =

\ ~

1 = 0'

+ 0

• 1

- 2 = -2,

= г

- с

= 0

•

3 + 0

• 1

- 3= -3.

Исходный опорный план (0,0,300,150) не является опти-

мальным, так как среди оценок Ау имеются отрицательные.

Переход к новому опорному плану осуществим, введя в базис

вектор А

, имеющий минимальную отрицательную оценку..

Определяем вектор, выходящий из базиса:

. f300 150^

1пп

Q = mini —, —I = 100,

т.е.

вектор Аз следует вывести из базиса. Главным направ-

ляющим элементом является а^ = 3 (выделен рамочкой).

Переход к следующей симплекс-таблице осуществляем с по-

мощью преобразований Жордана-Гаусса.