Фёдоров А.Ф., Кузьменко Е.А. Системы управления химико-технологическими процессами: учебное пособие

Подождите немного. Документ загружается.

Федоров А.Ф.,Кузьменко Е.А.«Системы управления

химико-технологическими процессами»,

пособие, 2009 г

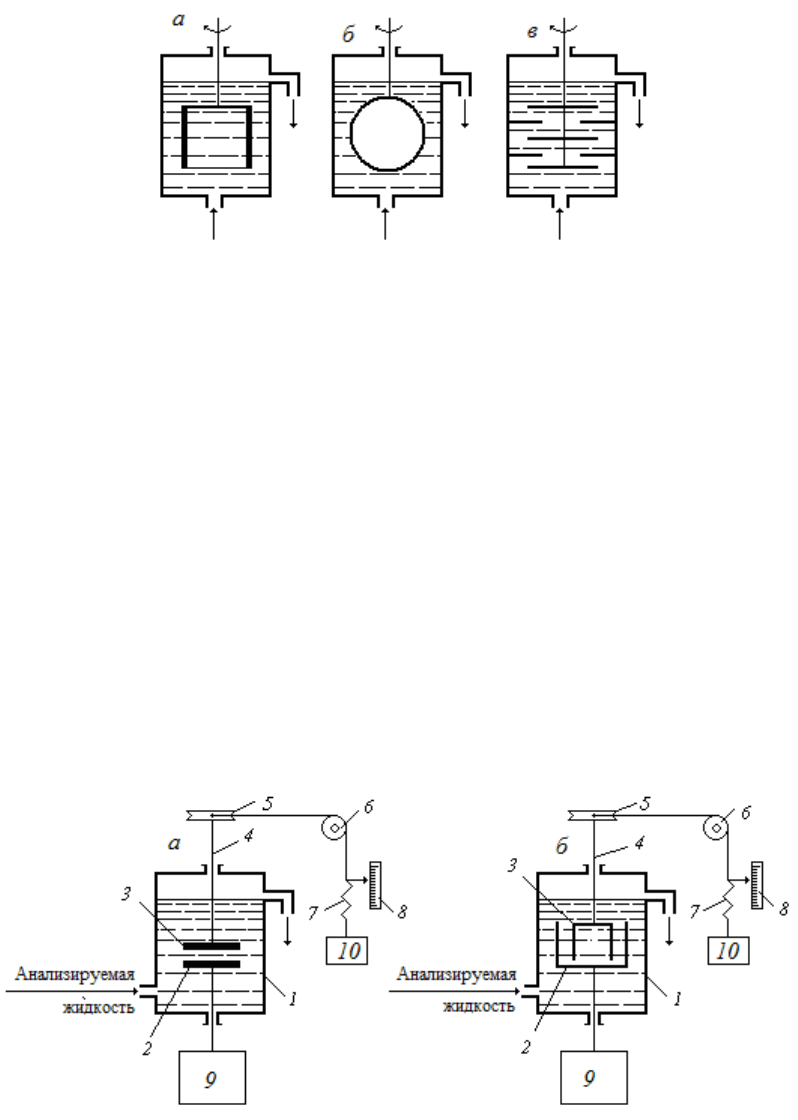
Рис. 7.28. Схемы ротационных вискозиметров

В качестве тела вращения используется цилиндр (рис. 7.28, а), шар

(рис. 7.28,

б) или диски, закрепленные на валу (рис. 7.28, в). Диски вра-

щаются между шайбами, закрепленными на стенках сосуда. Наиболь-

шее распространение получили вискозиметры с коаксиальными цилин-

драми (см. рис. 7.29).

Момент вращения создается диском

2 (см. рис. 7.29, а) или цилин-

дром

2 (см. рис. 7.29, б), вращательное движение которым сообщает

синхронный двигатель

9. На диске 3 (цилиндре 3) возникает момент

вращения, передаваемый анализируемой жидкостью. Этот момент с

помощью вала

4 передается на шкив 5 и через шкив 6 передается на

пружину

7, которая компенсирует развиваемое усилие, пропорциональ-

ное динамической вязкости анализируемой среды. Преобразователь

преобразует это усилие в унифицированный пневматический или элек-

трический сигнал. Класс точности – 1,0–2,5.

Рис. 7.29. Схемы коаксиальных вискозиметров

Измерительные комплекты коаксиальных вискозиметров содержат

первичный преобразователь ПП, преобразующий значение динамиче-

ской вязкости в усилие

F, которое промежуточным преобразователем

ППр типа «усилие – давление» или «усилие – ток» преобразуется в

унифицированный сигнал давление или ток, измеряемые прибором вто-

ричным ПВ (рис. 7.30).

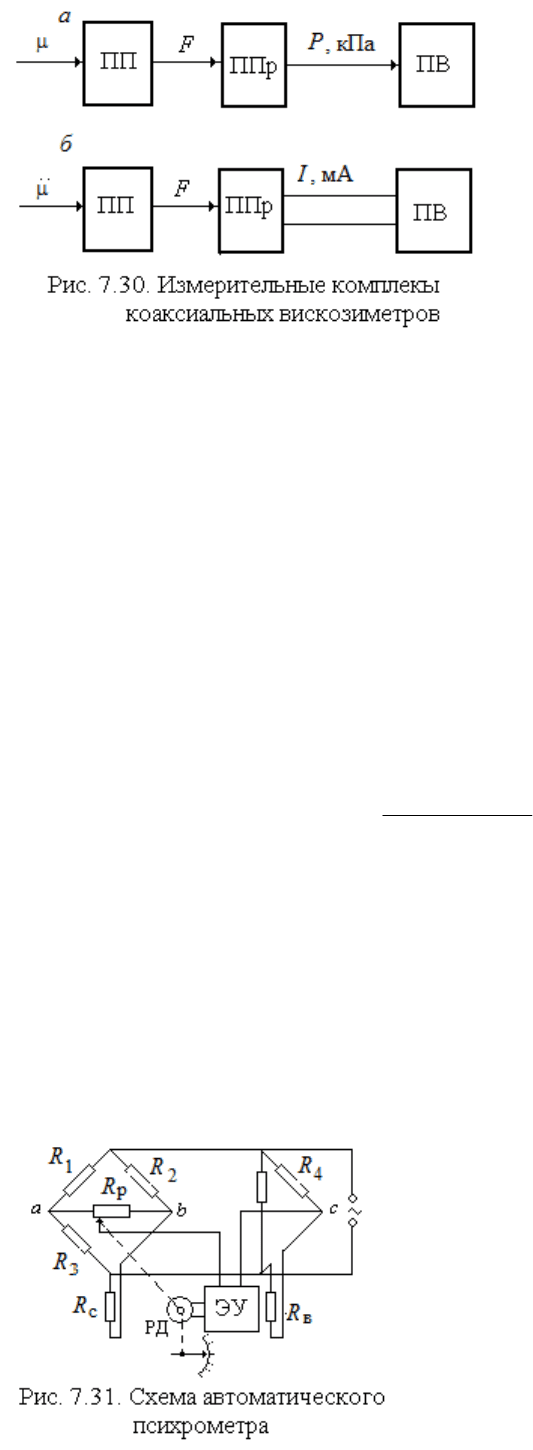
Федоров А.Ф.,Кузьменко Е.А.«Системы управления

химико-технологическими процессами»,

пособие, 2009 г

7.10. Измерение влажности

газов и сыпучих материалов

Под влажностью газа или

сыпучего материала понимают

содержание влаги в единице

объема. Основная единица из-

мерения

абсолютной влажно-

сти

– килограмм на метр куби-

ческий (кг/м

Под

относительной влажностью понимают отношение массы

водяного пара, содержащегося в 1 м

газа, к максимально возможной

массе водяного пара в 1 м

того же газа при той же температуре и дав-

лении. Единица измерения относительной влажности – %.

Автоматическое измерение влажности газов производится психро-

метрическим методом, методом точки росы и сорбционным методом.

Автоматические психрометры для измерения влажности газа

используют психрометрический эффект: при испарении влаги с увлаж-

ненной поверхности термометра (влажный термометр) температура его

снижается. Между «сухим» и «влажным» термометром создается раз-

ность температур, называемая

психрометрической разностью.

Зависимость относительной влажности

(%) от психрометриче-

ской разности имеет вид

100

)(

всв

ttAP

−

=ϕ

, (7.32)

где

– давление паров, насыщающих анализируемую газовую смесь

при температуре «влажного» термометра

t ;

P – давление паров, на-

сыщающих анализируемую газовую смесь при температуре «сухого»

термометра

t ; A – психрометрический коэффициент, зависящий от

конструкции психрометра, скорости обдувания влажного термометра

газом и давления газа.

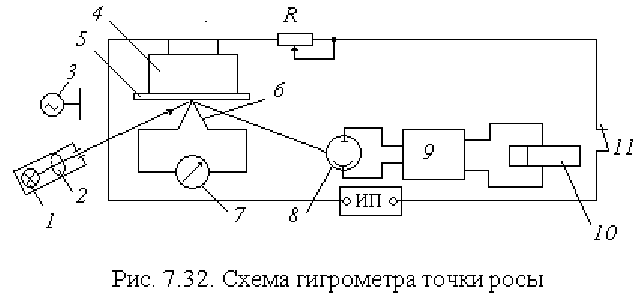
Измерительная схема автоматического психрометра построена на

базе двух неуравновешенных мостов

(рис. 7.31). Один мост образован рези-

сторами

R ,

R и

R ; в измери-

тельную диагональ

ab включен рео-

хорд

R . Другой мост образован рези-

сторами

R ,

R и

R . Таким обра-

зом, разность потенциалов на верши-

нах

a и b пропорциональна температу-

Федоров А.Ф.,Кузьменко Е.А.«Системы управления

химико-технологическими процессами»,

пособие, 2009 г

ре «сухого» термометра сопротивления, а разность потенциалов на

вершинах

a и c пропорциональна температуре «влажного» термометра

сопротивления. Мосты включены встречно. В связи с этим падение на-

пряжения между вершинами

b и c пропорционально разности темпера-

тур «сухого» и «влажного» термометров. Напряжение небаланса ком-

пенсируется частью падения напряжения на реохорде

R , поэтому каж-

дому положению движка реохорда

R в состоянии равновесия будет

соответствовать определенная психрометрическая разность. При изме-

нении влажности анализируемой среды на входе электронного усилите-

ля появится напряжение небаланса, электронный усилитель ЭУ вклю-

чит реверсивный двигатель РД, выходной вал которого переместит

движок реохорда

R до состояния равновесия. Одновременно переме-

щается стрелка вторичного прибора. Основная абсолютная погреш-

ность влагомера – 3 %.

При охлаждении анализируемого газа наступает насыщение паров

влаги (

точка росы). При постоянном давлении точка росы не зависит

от температуры газа, а зависит только от влажности.

Полупроводниковая термоэлектрическая батарея

4 (рис. 7.32), ра-

ботающая по принципу Пельтье, охлаждает зеркало

5 до появления на

его поверхности конденсата. Отражательная способность зеркала резко

ухудшится, поэтому световой поток, поступающий от лампы накалива-

ния

1 через линзу 2 на фотоэлемент 8, уменьшится. Электронный блок 9

переключит поляризованное реле

10 и контакт 11 разомкнется, выклю-

чив питание термобатареи

4. Так как зеркало обдувается вентилято-

ром

3, то конденсат на зеркале испаряется, отражательная способность

зеркала восстанавливается и световой поток поступает на фотоэле-

мент

8. Электронный блок 9 переключит поляризованное реле 10 так,

что контакт

11 замкнется. Включится питание термобатареи. Зеркало

охлаждается. Цикл повторяется. Температура поверхности зеркала из-

меряется термопарой

6 и милливольтметром 7. Практически реализова-

на следящая система, поддерживающая температуру зеркала равной

температуре точки росы.

Федоров А.Ф.,Кузьменко Е.А.«Системы управления

химико-технологическими процессами»,

пособие, 2009 г

Сорбционные методы

основаны на поглощении влаги из анализи-

руемой газовой смеси каким-либо гигроскопическим веществом. При

этом может меняться электрическая проводимость пленки; изменяется

количество электричества, затрачиваемого на электролиз влаги; изме-

няется частота собственных колебаний кварцевого резонатора от массы

вещества, нанесенного на поверхность кварцевой пластины; изменяется

масса поглотителя влаги и т. д.

Для

определения

влажности сыпучих материалов используются

прямые методы высушивания, экстракционные и химические. Эти ме-

тоды неавтоматические, требующие длительного времени для анализа.

Их используют в лабораторной практике.

Косвенные методы позволяют быстро определить влажность, но

дают большую погрешность. Достоинство состоит в том, что эти мето-

ды позволяют автоматизировать процесс измерения влажности.

Кондуктометрический метод использует зависимость электри-

ческих свойств капиллярно-пористых материалов от влагосодержания.

Электрическое сопротивление

таких материалов определяется по

выражению

WAR /= , (7.33)

где

A – постоянная, зависящая от материала; W – влажность материала

в % по массе;

n – показатель степени, зависящий от структуры и приро-

ды материала.

Кондуктометрический метод пригоден для создания сигнализато-

ров и индикаторов, не обеспечивающих высокую точность измерения.

Электрическое сопротивление материала измеряется с помощью мосто-

вых схем.

Диэлькометрический метод основан на зависимости электриче-

ской емкости преобразователя, выполненного в виде двух пластин или

двух соосных цилиндров и заполненного анализируемым материалом,

от влажности. Измерительные схемы строятся на основе неуравнове-

шенных мостов.

Федоров А.Ф.,Кузьменко Е.А.«Системы управления

химико-технологическими процессами»,

пособие, 2009 г

8. АВТОМАТИЧЕСКИЕ СИСТЕМЫ

РЕГУЛИРОВАНИЯ

8.1. Основные понятия и определения

Многие задачи управления технологическими процессами (рис. В.1)

можно решить путем стабилизации технологических параметров объекта

относительно их заданных значений, то есть реализовать частный случай

автоматического управления, получившего название

регулирование.

Регулированием называют поддержание выходных параметров

объекта относительно их заданных значений, постоянных или пе-

ременных, путем изменения подачи регулирующих воздействий.

Ес-

ли этот процесс осуществляется с помощью технических средств без

участия человека, то он называется

автоматическим.

Под объектом регулирования понимают аппарат или совокуп-

ность аппаратов, в которых осуществляется регулируемый про-

цесс

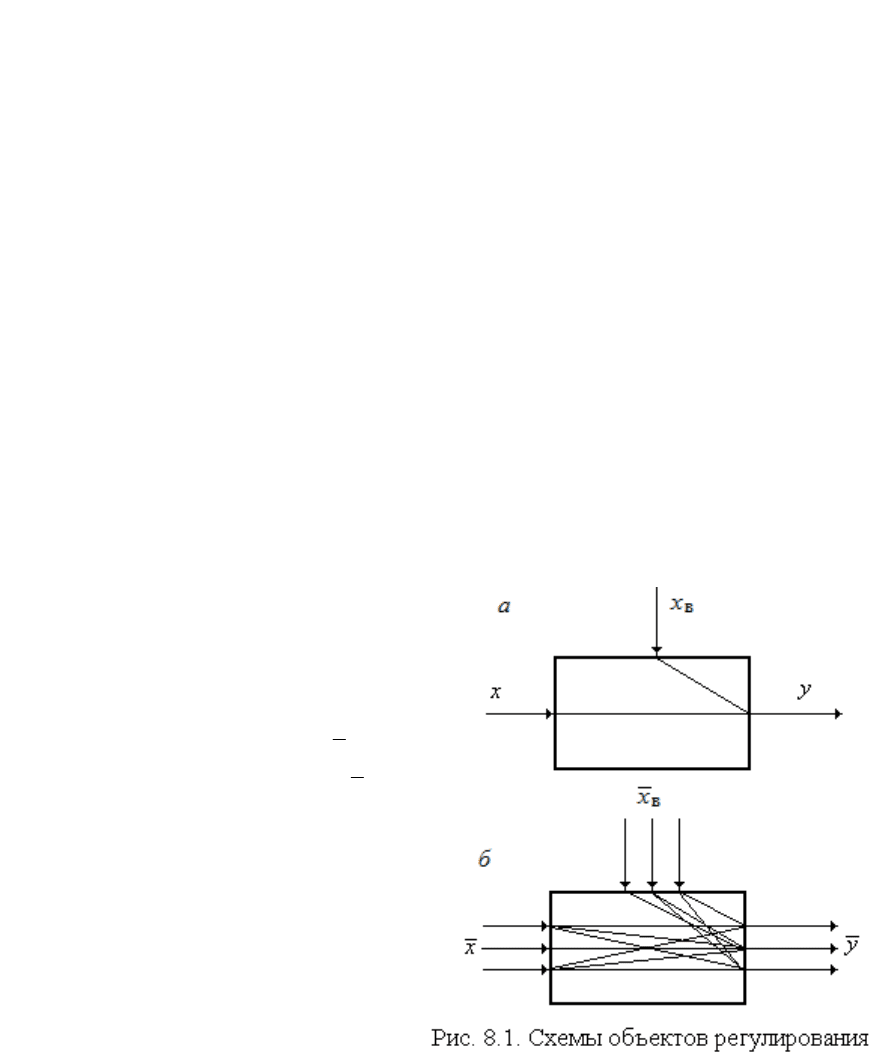
Если

объект имеет один ре-

гулируемый параметр

y и регули-

рующее воздействие

x, то он назы-

вается

одномерным (рис. 8.1, а).

Если

объект имеет несколько

регулируемых параметров

y и

регулирующих воздействий

, то

он называется

многомерным

(рис. 8.1,

б). Если внутренние

связи между регулируемыми па-

раметрами отсутствуют или ими

можно пренебречь, то такой объ-

ект называется

объектом с несвя-

занными параметрами.

Если

внутренние связи между регули-

руемыми параметрами присутствуют, то такой объект называется

объек-

том со связанными параметрами

Кроме регулирующих воздействий x (изменение расхода массы

или энергии с помощью специальных исполнительных устройств –

ре-

гулирующих органов

), на объект действуют внутренние или внешние

возмущения

x (изменение температуры окружающей среды, измене-

ние состава сырья, колебание давления и т. д.).

В качестве

средств получения информации используются рас-

смотренные в предыдущих разделах измерительные приборы и преоб-

Федоров А.Ф.,Кузьменко Е.А.«Системы управления

химико-технологическими процессами»,

пособие, 2009 г

разователи (датчики), работающие в автоматическом режиме.

В соответствии с поставленной

перед автоматической системой

регулирования (АСР)

задачей – обеспечить поддержание регулируемо-

го параметра в некоторой малой окрестности относительно его заданно-

го значения – вместо устройства управления используется

автомати-

ческий регулятор.

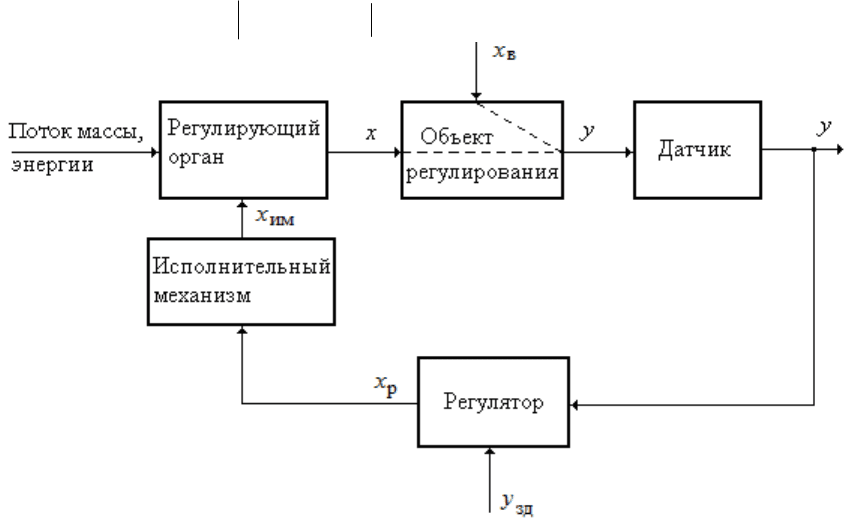
Под действием внешних или внутренних возмущений изменяется

значение

регулируемого параметра y (рис. 8.2). Датчик (измеритель-

ный преобразователь) преобразует регулируемый параметр в унифици-

рованный электрический или пневматический сигнал

y, который посту-

пает на вход

регулятора. Здесь текущее значение y сравнивается с за-

данным значением

зд

y и по определенному закону, реализуемому ре-

гулятором (

закон регулирования, или алгоритм), преобразуется в ре-

гулирующее воздействие

x , которое поступает на исполнительный

механизм

, перемещающий регулирующий орган. Последний изменяет

расход массы или энергии в объект до тех пор, пока отклонение теку-

щего значения регулируемого параметра не станет меньше некоторого

заданного значения

Δ≤−τ

зд

)( yy .

Рис. 8.2. Схема одноконтурной системы регулирования по отклонению

Таким образом, регулятор формирует регулирующее воздействие,

постоянно оценивая результат работы системы по величине отклонения

регулируемого параметра от заданного значения. Такой способ регули-

рования получил название

«регулирование по отклонению». Реализа-

ция способа возможна благодаря использованию

обратной связи, ко-

торая обеспечивает передачу информации с выхода системы на вход и

Федоров А.Ф.,Кузьменко Е.А.«Системы управления

химико-технологическими процессами»,

пособие, 2009 г

создает замкнутый контур регулирования.

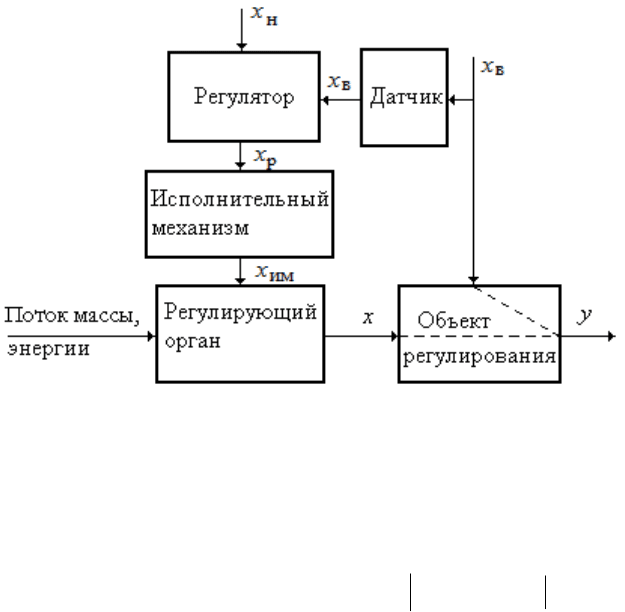
Системы, работающие по принципу компенсации возмущения,

не имеют замкнутого контура регулирования и поэтому не анали-

зируют результат

(рис. 8.3).

Рис. 8.3. Схема системы регулирования по возмущению

Датчик измеряет величину возмущающего воздействия и преобра-

зует в унифицированный сигнал

x , который поступает в регулятор, где

сравнивается с номинальным значением

x. Если отклонение текущего

значения мало отличается от номинального

внв

)( Δ≤−τ xx , то систе-

ма находится в равновесии. Если отклонение превысит величину

Δ , то

регулятор преобразует это отклонение по заданному закону в регули-

рующее воздействие

x , исполнительный механизм с помощью регу-

лирующего органа изменит поток массы или энергии в объект, чтобы

компенсировать влияние возмущения на величину регулируемого па-

раметра, не дожидаясь его изменения. Реализуется принцип опережения

воздействия по отношению к реакции системы. В этом случае алгоритм

регулятора с большой точностью должен учитывать статические и ди-

намические

свойства в

сей системы. Достичь этого в абсолютном боль-

шинстве случаев не удается в связи со сложностью технологических

процессов, поэтому используются комбинированные системы, соче-

тающие положительные свойства систем регулирования по отклонению

и по возмущению (см. рис. 8.4).

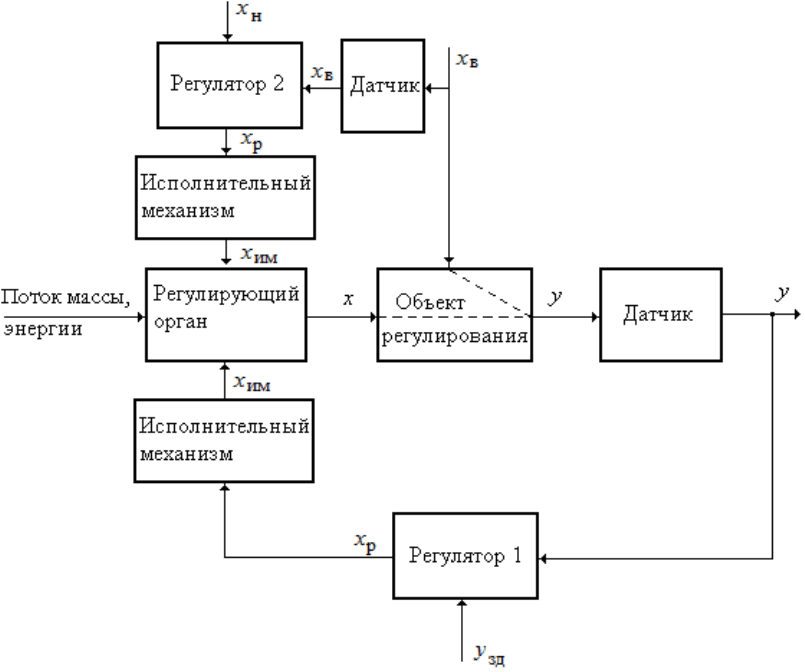
Выбирается внешнее возмущающее воздействие, оказывающее

наибольшее влияние на процесс, и строится система компенсации влия-

ния этого

возмущения на ба

зе регулятора 2. Влияние остальных возму-

щений компенсируется АСР, работающей по принципу отклонения

и реализованной на базе регулятора

Федоров А.Ф.,Кузьменко Е.А.«Системы управления

химико-технологическими процессами»,

пособие, 2009 г

Рис. 8.4. Схема комбинированной системы регулирования

В зависимости от способа формирования заданного значения

зд

регулируемой величины АСР делятся на стабилизирующие, программ-

ные и следящие.

В стабилизирующей АСР задатчик формирует постоянное во вре-

мени значение

const)(

зд

=τy , поэтому задача стабилизирующей АСР

заключается в поддержании регулируемого параметра в некоторой

малой окрестности относительно его заданного значения, остаю-

щегося постоянным длительное время.

В АСР программного регулирования задатчик формирует задание

по заранее определенной во времени программе

)()(

зд

fy , поэтому

задача программной АСР заключается в изменении регулируемого

параметра в соответствии с заданной программой.

В следящих АСР задание формируется в зависимости от изменения

другого параметра –

)(

1зд

yfy = , поэтому задача следящей АСР за-

ключается в изменении регулируемого параметра во времени в опре-

деленной зависимости от изменения другого параметра –

y , то есть

необходимо следить за изменением параметра

y и воспроизводить ре-

гулируемый параметр в определенной зависимости от его изменения:

Федоров А.Ф.,Кузьменко Е.А.«Системы управления

химико-технологическими процессами»,

пособие, 2009 г

[

]

)()(

yfy .

непрерывных АСР непрерывному изменению регулируемого па-

раметра соответствует непрерывное изменение выходных величин всех

элементов системы.

релейных АСР имеется релейное звено, на выходе которого фор-

мируется два (или три) фиксированных значения сигнала при непре-

рывном изменении входного сигнала.

импульсных АСР имеется импульсное звено, преобразующее

непрерывный входной сигнал в последовательность импульсов, ампли-

туда или длительность которых пропорциональна входному сигналу.

АСР с

цифровыми вычислительными устройствами работают

в импульсном режиме, так как выходной сигнал вычислительного уст-

ройства представляет собой последовательность импульсов.

В зависимости от природы регулируемого параметра АСР делятся

на АСР температуры, давления, расхода, уровня, концентрации и т. д.

8.2. Математическое описание АСР и их элементов

Для синтеза и анализа АСР используется аппарат алгебраических

и дифференциальных уравнений.

В связи с тем, что АСР имеют в своем составе элементы различной

природы, то их математическое описание строится в терминах той дис-

циплины, к которой относится процесс, происходящий в элементе.

В химической и в других отраслях промышленности даже в отдельных

элемент

ах протекают процессы различной природы (гидродинамиче-

ские, тепловые, массообменные, химические), поэтому аппарат алгеб-

раических и дифференциальных уравнений является универсальным

для математического моделирования процессов любой природы. Осо-

бенно это касается исследования процессов в АСР, где все элементы

взаимосвязаны.

АСР могут находиться в равновесном (статическом) и неравновес-

ном (динамическом) состоянии.

Равновесное состояние характеризуется постоянством во вре-

мени всех параметров системы,

и её поведение определяется статиче-

ской характеристикой:

)(

xfy

, (8.1)

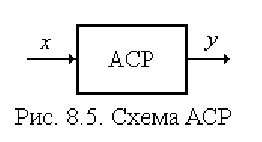
где

y и

x – значения выходного и входного параметров системы

в равновесном состоянии (рис. 8.5).

Обычно статические характеристики АСР и

её элементов могут быть представлены в виде

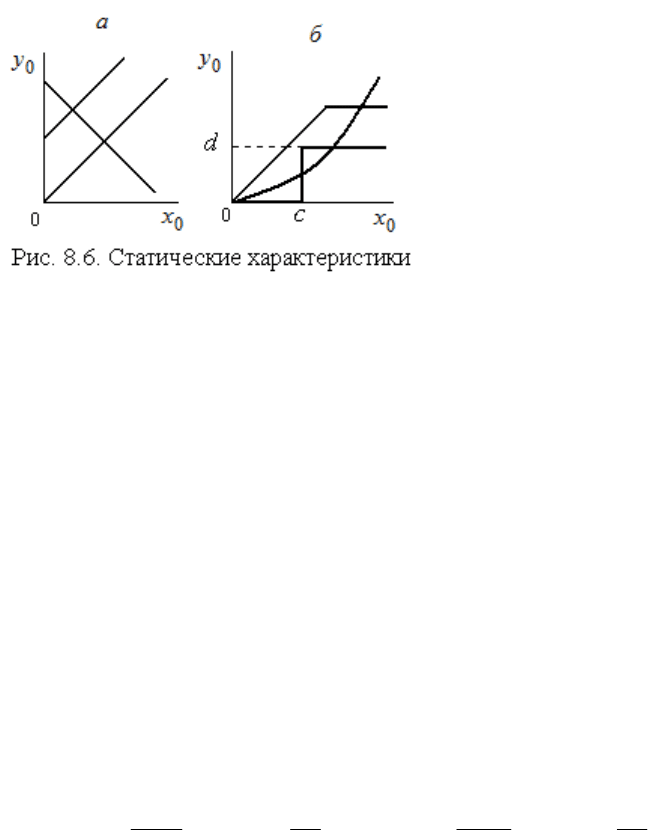
алгебраических уравнений и графиков (рис. 8.6).

Если статическая характеристика сис-

Федоров А.Ф.,Кузьменко Е.А.«Системы управления

химико-технологическими процессами»,

пособие, 2009 г

темы или элемента линейная, то система или элемент называют-

ся линейными

(рис. 8.6, а).

Общий вид линейной статической характеристики можно предста-

вить в виде алгебраического уравнения

kxay

, (8.2)

где а – постоянная величина; k – ко-

эффициент усиления.

Если статическая характе-

ристика системы или элемента

нелинейная, то система или эле-

мент называются нелинейными

(рис. 8.6, б), и её поведение опреде-

ляется нелинейным алгебраическим

уравнением. Например, уравнение

статики релейного звена (рис. 8.6,

б) запишется в следующем виде:

⎩

⎨

⎧

≥

≤

.пр

;при0

cxиd

y (8.3)

неравновесном режиме, возникающем под действием возмуще-

ний и регулирующих воздействий,

поведение системы описывается

уравнениями динамики ),()(

y или динамическими характери-

стиками

, которые определяют зависимость изменения выходной

величины во времени от изменения входной величины

. Динамические

характеристики АСР или элемента могут быть представлены в виде

дифференциальных уравнений, передаточных и переходных функций

и в виде частотных характеристик.

Динамические характеристики линейных АСР описываются обык-

новенными дифференциальными уравнениями вида

bya

0101

……

, (8.4)

где a

, a

,…, a

, b

,…,b

– постоянные коэффициенты; τ – вре-

мя; n – порядок левой части уравнения; m – порядок правой части урав-

нения; y – изменение выходной величины; x – известное входное воз-

действие.

В соответствии с условием физической реализуемости систем по-

рядок правой части уравнения не должен превышать порядок левой час-

ти, или m ≤n.

При x=0 уравнение (8.4) преобразуется

в однородное уравнение