Faulon J.L., Bender A. Handbook of Chemoinformatics Algorithms

Подождите немного. Документ загружается.

48 Handbook of Chemoinformatics Algorithms

16. Draw Link/Chain

17. Rank Ordern+1Substituents

18. End Do

19. Do Until All Order n Substituents Positioned

20. Select Unpositioned Order n Substituent

21. Position Order n Substituent

22. End Do

23. Position Order 1 Substituent

24. End Do

25. Position Ring

26. End Do

27. End

Other 2D chemical structure drawing algorithms that are independent of a ring

system database have been developed. Some use ring perception algorithms [25] such

as the drawing algorithm of Shelley [26], which also employs the Morgan extended

connectivity index (cf. Section 2.3 and [27]). Morgan indices are calculated for atoms

and ring systems and are used for minimizing atom crowding during assignment of

2D coordinates, for ring system orientation, and for identifying invariant coordinates

for ring systems.

The depiction of 2D structures has been reviewed by Helson [28]. Other algo-

rithms have been developed such as those by Weininger for SMILES strings [29],

by Fricker et al. [30], by Stierand et al. [31], and by Clark et al. [32] for the Molec-

ular Operating Environment (MOE) software suite (Chemical Computing Group,

http://www.chemcomp.com). Fricker et al. also rely on the sequential assembly of

chains and rings and proposed an algorithm for drawing structure under directional

constraints on bonds [30]. Stierand et al. proposed a method for generating diagrams

for protein–ligand complexes that highlights the interaction between amino acids and

ligand atoms on a 2D map [31].

The algorithm of Clark et al. [32] partitions a molecular graph into segments,

generates local structural options for each segment, assembles local options by random

sampling, and selects the minimally congested assembly as the basis for the final

output. The algorithm identifies ring systems, atom chains, lone atoms, atom pairs,

and stereochemistry for a hydrogen-suppressed molecular graph. The structural units

generated are assigned geometric constraints in internal coordinates such that a set

of distances and angles between atoms in the structural units is obtained. Rings are

identified using an algorithm that finds the smallest set of smallest rings [8,9]. Atom

chains are generated using a small set (C, N, O, and S) of neutral, acyclic atoms

connected by single bonds. Lone atoms are constrained with standard values for

bond lengths and angles. Atom pairs are constrained to preserve local geometry and

stereochemistry.A core ring system is identified by removing rings that share only one

edge with any other ring and coordinates are assigned to the core ring system based on

a database of ring templates. The candidate structures obtained during the assembly

of structural units in the sampling step are screened using a congestion function, with

the solution structure having the lowest congestion. In the postprocessing step the

solution structure is adjusted for aesthetic depiction. Thus, atoms in close contact

are permitted to deviate slightly; atoms or bonds may be rotated to relieve overlap;

Algorithms to Store and Retrieve Two-Dimensional (2D) Chemical Structures 49

connected fragments may also be brought to a horizontal position by rotation; and

hydrogen atoms are expressed for cases where explicit hydrogen atom depiction is

mandated. The MOE 2D chemical drawing algorithm was extensively evaluated and

demonstrated high performance using both statistical metrics and human evaluation.

Other software systemsavailable includethose from OpenEye (Ogham) andAdvanced

Chemistry Development (ChemSketch).

An important aspect of the use of chemical databases by chemoinformatics systems

is their inspection, refinement, and standardization prior to use. This ensures, for

example, that a chemical compound with multiple representations (such as Kekulé

structures or tautomers) is correctly identified and processed by an application. Special

tools such as sdwash (Chemical Computing Group, http://www.chemcomp.com) and

Standardizer (ChemAxon, http://www.chemaxon.com) are available to assist with

such problems. These tools may work by removing salt and solvent molecules, adding

or removing hydrogens, identifying aromaticity, or enumerating protonation states and

tautomers. Conjugated systems can be recognized using aromaticity perception [33]

or identification of alternating bonds [34].

Perception of tautomers has also received considerable attention in chemoinfor-

matics. Tautomers are isomers of organic compounds that result from migration of

a hydrogen atom or a proton accompanied by a switch between adjacent single and

double bonds. Tautomerism is an important property because different tautomers of

a compound may give different results in virtual screening and for properties based

on atom-type parameters. Several approaches have been suggested for the treatment

of tautomers in chemical databases and applications [35–38].

Another area of chemoinformatics that has seen active development for a number

of years is searching for Markush structures in patent databases [39]. A Markush

structure is a generalized notation of a set of related chemical compounds and may

be used in patent applications to define a substance that has not yet been synthesized.

Searching for Markush structures in chemical databases enables a researcher to rule

out priority in patent applications. Chemical drawing programs can represent these

structures by, for example, drawing a bond to the center of a phenyl ring indicating

substitution at any position in the ring (Figure 2.3).

OCH

FIGURE 2.3 Markush structure for methylphenidate ester with a generalized R group

substitution at any position in the phenyl ring.

50 Handbook of Chemoinformatics Algorithms

2.3 STORING AND RETRIEVING CHEMICAL STRUCTURES

THROUGH CANONICAL LABELING

When storing a chemical structure in a database, one is faced with the problem of deter-

mining whether the structure is already present in the database. Therefore, one needs

to determine whether structures are identical. In graph theory two identical graphs

are said to be isomorphic, and an isomorphism is a one-to-one mapping between the

atoms of the graph preserving the connectivity of the graphs. When two atoms of

the same graph are mapped by an isomorphism, the two atoms are said to be auto-

morph and one uses the term automorphism instead of isomorphism. Atoms that are

automorph are symmetrical (or equivalent), and in a given molecular graph, atoms

can be partitioned into their automorphism group or equivalent classes. One prac-

tical procedure to detect isomorphism or automorphism between molecular graphs

is to canonically (i.e., uniquely) label the atoms of the graphs. Two graphs are then

isomorphic if they have the same labels.

Automorphism partitioning and canonical labeling are of significant interest in

chemistry. Both problems have practical applications in (1) molecular topological

symmetry perception for chemical information and quantum mechanics calculations,

(2) computer-assisted structure elucidation, (3) NMR spectra simulation, and (4)

database storage and retrieval, including determination of maximum common sub-

structure. Since 1965 [27] many canonical labeling methods have been proposed in the

context of chemical computation, and this section presents three of them after provid-

ing more precise definition and relationships between isomorphism, automorphism,

and canonical labeling.

2.3.1 TERMINOLOGY

Two given graphs are isomorphic when there is a one-to-one mapping (a permutation)

from the vertices of one graph to the vertices of the second graph, such that the edge

connections are respected. An isomorphic mapping of the vertices onto themselves is

called an automorphism. The set of all automorphisms of a given graph is the automor-

phism group of the graph. The automorphism group contains information regarding

the topological symmetry of the graph. In particular, the orbits of an automorphism

group identify symmetrical (or equivalent) vertices. The canonical labeling problem

consists of finding a unique labeling of the vertices of a given graph, such that all

isomorphic graphs have the same canonical labels. Examples of canonical represen-

tations are graphs that maximize (or minimize) their adjacency matrices. Two graphs

with the same canonical representation are isomorphic. This observation is used when

querying chemoinformatics databases as the structures stored in chemoinformatics

databases are canonized prior storage. The obvious advantage is that isomorphism

is reduced to comparing the canonical labels of the input structure with those of the

database.

Although most articles related to graph isomorphism have been published in the

computer science literature, the computation of the orbits of automorphism groups

using partitioning techniques has received most attention in chemistry and the two

problems have been shown to be computationally equivalent [40]. The canonical

Algorithms to Store and Retrieve Two-Dimensional (2D) Chemical Structures 51

labeling problem has been studied in both chemistry and computer science. It would

appear that the canonical labeling problem is closely related to the isomorphism

testing problem; the latter can be performed at least as fast as the former, and for many

published algorithms, isomorphism tests either include a procedure for canonization

or else have an analogue for that problem [41].

Since canonical labeling can be used to detect isomorphism, the remainder of this

section focuses on canonization procedures. As already mentioned, several canoni-

cal labeling methods have been proposed in the context of chemical computation,

and three of them are presented next. The general characteristic of these meth-

ods is the use of graph invariants to perform an initial vertex partitioning. Graph

invariants can be computed efficiently and have led to the development of fast

algorithms. For most published algorithms, the initial vertex partitioning is fol-

lowed by an exhaustive generation of all labelings. The computational complexity

of the exhaustive generation can be reduced using the fact that two vertices with

different invariants belong to different equivalent classes; hence, exhaustive label-

ing generation is performed only for vertices with the same invariant. Nonetheless,

because all vertices may have the same invariant, the upper bound of the time com-

plexity for the exhaustive labeling generation scales exponentially with the number

of vertices.

Whereas vertices with different invariants belong to different equivalent classes,

the reverse is not necessarily true. As a matter of fact, isospectral points are vertices

with the same invariant that belong to different classes [42]. Although the invariant

approach may not be totally successful in the sense that the proposed methods work

in all cases, it has been shown to behave well on average [43,44]. Indeed, for a given

random graph there is a high probability that its vertices can be correctly partitioned

using graph invariants [45].

To simplify the presentation, the three canonization algorithms given next are

illustrated for hydrocarbons and do not take stereochemistry into account. For each

algorithm, the reader is referred to relevant literature on how the algorithms can be

modified to incorporate heteroelements and stereochemistry.

2.3.2 MORGAN’S ALGORITHM

This historically important algorithm was first published in 1965 by H.L. Morgan [27]

and was part of the development of a computer-based chemical information system

at the CAS. The original algorithm did not take into account stereochemistry, and an

extension was proposed in 1974 by Wipke et al. [46]. We present below a scheme

based on Morgan’s algorithm; while our scheme may not be the exact published

algorithm, it captures the essential ideas.

As with many canonization methods, Morgan’s algorithm proceeds in two steps.

In the first step, graph invariants (cf. the definition in Chapter 1) are calculated for

each atom. In the second step, all possible atom labels are computed and printed

according to the invariants. Invariants are calculated in a recursive manner. At each

recursive iteration, the invariant of any given atom is the sum of the invariants of

its neighbors computed in the previous step. The process starts by assigning to all

atoms an initial invariant equal to 1 or equal to the number of neighbors of that atom

52 Handbook of Chemoinformatics Algorithms

(as in the original algorithm published by Morgan). One notes that when assigning

an initial invariant equal to 1, the invariant obtained at the next iteration equals the

number of neighbors. The recursive procedure stops when the largest number of

distinct invariants is obtained, that is, at an iteration for which the number of invariants

remains the same or decreases after that iteration. Labeling of the atoms is performed

using the invariants found at the stopping iteration. One starts by choosing the atom

with the largest invariant; this atom is labeled 1. One notes that all the other atoms

are unlabeled at this point. At the second step, the neighbors of the atom labeled 1

are sorted in decreasing order of invariants; the neighbors are then labeled 2, 3, and

so on, in the order that they appear in the sorted list. There may be several ways of

sorting the neighbors; as some atoms may have the same invariants, the algorithm

computes all the possible sorted lists. At the next step, one searches for atoms with

the smallest label having unlabeled neighbors and the procedure described in the

second step is repeated, this time for the smallest labeled atom. The procedure halts

when all atoms have been labeled. The canonical graph is the one producing the

lexicographically smallest list of bonds when printing the graph. In the algorithm

given below, the notation  is used to depict the number of distinct elements of

a list, and the routine print-graph() prints the edges of a graph for a given list of

atom labels.

ALGORITHM 2.2 MORGAN’S ALGORITHM

canonical-Morgan(G)

input: - G: a molecular graph

output: - printout of graph G with computed labels

01. Let inv be the set of invariant initialized to

{1, 1, ..., 1}

02. Let lab be the set of labels initialized to

{0, 0, ..., 0}

03. inv = compute-invariant(G,inv)

04. Let L be the set of atoms in G with the largest

invariant

05. For all atom x in L do

06. lab(x) = 1

07. compute-label(G,inv,lab,1)

08. lab(x) = 0

09. done

compute-invariant(G,inv)

input: - G: a molecular graph

- inv: the initial invariants for all atoms

output: - INVARIANT: the updated invariants for all

atoms

01. For all atom x of G do

02. INVARIANT(x) =



[x,y] in G

inv[y]

03. done

04. if |INVARIANT|>|inv|

Algorithms to Store and Retrieve Two-Dimensional (2D) Chemical Structures 53

05. then return(compute-invariant(G,INVARIANT))

06. else return(inv)

07. fi

compute-label(G,inv,label,n)

input: - G: a molecular graph

- inv: the invariants for all atoms

- label: the labels for all atoms

- n: the current label

output: - printout of graph G with computed labels

01. Let x be the atom of G with the smallest label

having a non empty list L

of unlabeled

neighbors

02. if (x cannot be found) then

03. print-graph(G,label)

04. return

05. fi

06. For all lists S

corresponding to the list L

where

neighbors of x are sorted by decreasing invariants do

07. For all atoms y in S

do n = n + 1, label(y)= n done

08. compute-invariant(G,inv,label,n)

09. For all atoms y in S

do n = n − 1, label(y) = 0 done

10. done

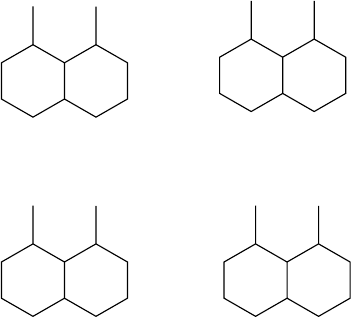
The invariant step of Morgan’s algorithm is illustrated in Figure 2.4 for 1,8-

dimethyl-decahydronaphthalene; the labeling step is illustrated in Figure 2.5 for the

1 1

(1) Number invariant = 1 (3) Number invariant = 6

(2) Number invariant = 3 (4) Number invariant = 5

1 1

6 6

3 3

FIGURE 2.4 Invariant calculation with Morgan’s algorithm. The final list of invariants is

computed the first time the largest numbers of distinct invariant is obtained, the list of graph

(3) in the present case.

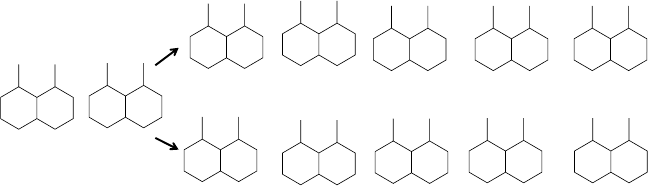
54 Handbook of Chemoinformatics Algorithms

810

11 12

810

FIGURE 2.5 Atom labeling with Morgan’s algorithm. The labels are computed according to

the invariants of graph (3) of Figure 2.4. The figure illustrates the fact that there are two ways

of sorting the list of neighbors of atom labeled 2 (graph C1 and graph C2). Graph G1 produces

the list of edges [1, 2] [1, 3] [1, 4] [2, 5] [2, 6] [3, 7] [3, 8] [4, 9] [4, 10] [5, 11] [6, 12] [7, 11]

[9, 12] and graph G2 produces the list [1, 2] [1, 3] [1, 4] [2, 5] [2, 6] [3, 7] [3, 8] [4, 9] [4, 10]

[5, 11] [6, 12] [7, 12] [9, 11]. G1 is canonical.

same compound. Graph G1 is the canonical graph, that is, the graph producing the

smallest lexicographic list of edges.

The main criticism of Morgan’s algorithm is the ambiguity of the summation

when computing atom invariants. Indeed, let us suppose that two three-connected

atoms have neighbors with respective invariants (1, 1, 3) and (1, 2, 2). After iterating

Morgan’s algorithm, these two atoms will have the same invariant 5, and the two

atoms will be considered to be equivalent whereas they should not. To palliate this

problem, Weininger et al. [47] proposed a solution making use of prime numbers. In

this implementation the initial labels are substituted by primes, that is, to invariant

1 is associated number 2, to invariant 2 number 3, to invariant 3 number 5, and so

on. Next, instead of summing the invariants of the neighbors, the product of the

associated primes is computed. According to the prime factorization theorem, the

solution of Weininger et al. is unambiguous. This solution was implemented when

canonizing SMILES, as described in the algorithm given next.

2.3.3 THE CANONICAL SMILES ALGORITHM

The algorithm presented below is based on the 1989 work published by Weininger

et al. [47]. As in the previous case, the outlined algorithm is not the exact replica

of the one that was published but provides the general idea on how SMILES strings

are canonically ordered. Like Morgan’s algorithm, canonical ordering is performed

in two steps. Invariants are first computed and labels are assigned according to the

invariants. For each atom, the invariant is initialized taking into account (1) the num-

ber of connections, (2) the number of non-hydrogen bonds, (3) the atomic number,

(4) the sign of the charge, (5) the absolute value of the charge, and (6) the number

of attached hydrogen atoms. Next, invariants are computed using a method simi-

lar to the routine compute-invariant given in Algorithm 2.2. However, as mentioned

earlier, instead of summing the invariants of the neighbors, Weininger et al. used

the products of the primes corresponding to the invariants of the neighbors. At the

Algorithms to Store and Retrieve Two-Dimensional (2D) Chemical Structures 55

next step, atoms are labeled according to their invariants, the smallest label being

assigned to the atom with the smallest invariant. The atom with the same invariant

has the same label. To uniquely label each atom, Weininger et al. used a proce-

dure named “double-and-tie-break.” This procedure consists of doubling all labels

(label 1 becomes 2, label 2 becomes 4, and so on), then an atom is chosen in the

set of atoms having the smallest labels, and the label of that atom is reduced by

one. The labels thus obtained form a new set of initial invariants and the whole

procedure (invariant computation followed by label assignment) is repeated. The pro-

cess stops when each atom has a unique label, that is, when the number of labels

equals the number of atoms. In the algorithm given next, we assume that an initial

set of invariants has been computed, as described above, when calling the routine

canonical-SMILES for the first time. The routine compute-invariant is not detailed,

but is similar to the one given with Algorithm 2.2 replacing summation by prime

factorization.

ALGORITHM 2.3 THE CANONICAL SMILES ALGORITHM

canonical-SMILES(G,inv)

input: - G: a molecular graph

- inv: a set of initial invariants

output: - printout of a canonical SMILES string of

graph G

01. inv = compute-invariant(G,inv)

02. Let lab be the set of atom labels assigned in

increasing invariants order

03. if |lab|=|G| then print-SMILES(G,lab) fi

04. lab = new set of labels doubling each label value

05. Let L be the set of atoms with the smallest

label such that |L|≥2

06. For all atom x in L do

07. lab(x) = lab(x)-1 , canonical-SMILES(G,lab),

lab(x) = lab(x)+1

08. done

In their 1989 paper, Weininger et al. [47] do not recursively apply the canonical-

SMILES routine to all atoms in the list of tied atoms with the smallest label (list

L in Algorithm 2.3 lines 05–08) but to an arbitrary atom selected from that list.

Weininger et al. algorithm complexity thus reduces to N

log

(N) for a molecular

graph of N atoms. While this implementation is efficient, it may not necessarily be

correct. Algorithm 2.3 does not scale in polynomial time, as the list L may com-

prise all N atoms the first time it is computed, N −1 atoms the second time, N − 2

the third time, and so one, leading to an N! complexity. However, Algorithm 2.3

produces all potential canonical SMILES, the final canonical string being the lexi-

cographically smallest one. Printing SMILES (routine print-SMILES) is performed

starting with the atom with the smallest label. This atom becomes the root of a tree

for a depth-first search. As mentioned in Section 2.1.1, with SMILES notations,

branches are indicated with parentheses: “(‘to open the branch and’)” to close the

56 Handbook of Chemoinformatics Algorithms

branch. When printing canonical SMILES, the algorithm directs branching toward

the lowest label; assuming the atom labels for acetone C

−

O)–C are 1–4- (

3)-

2, one starts with the methyl group labeled 1 and then moves to the central carbon

labeled 4. The branch is composed of the smallest atom label attached to the central

carbon, that is, the second methyl group labeled 2; the final atom is thus the oxygen

labeled 3. The printed canonical SMILES string for acetone is thus CC(C)

O and not

CC(

O)C.

The latest developments in the search for a unique representation of chemical

structures are the InChI and InChIKey algorithms [48]. These algorithms are based

on the McKay general graph canonization algorithm [49]. Because the InChI algo-

rithm has never been formally published, it is difficult to present this complex

method just based on the technical manual. Instead we present another algorithm,

whose performances have been shown to be comparable to those of the McKay

technique [50].

2.3.4 CANONICAL SIGNATURE ALGORITHM

The method outlined below was first published in 2004 [50]. As with previous algo-

rithms, the method first assigns invariants to atoms and next labels the atoms from

the invariants. In the present case, invariants are computed based on atom signatures.

The formal definition of an atom signature is given in Chapter 4, but for the purpose

of this section we define the signature of an atom x in a molecular graph G as being

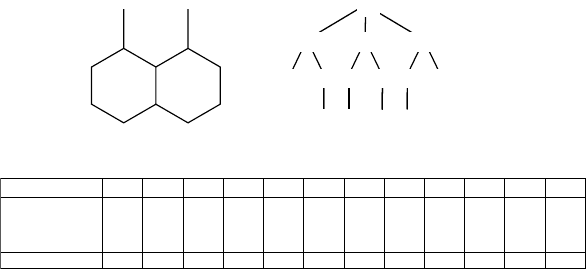
a tree T(x) spanning all the edges of the graph (cf. Figure 2.6a and b).

When computing an atom signature, the term tree is used in a somewhat loose

manner as several vertices in the tree may correspond to the same atom. The root

of the tree is atom x itself. The first layer of the tree is composed of the neighbors

of x; the second layer is composed of the neighbors of the vertices of the first layer

except atom x. The construction proceeds one layer at a time until no more layers

can be added, that is, until all the bonds of G have been considered. Assuming the

73 48

(a) (b)

(c)

Atom no. 1

C,0 C,1 C,1 C,1 C,2 C,2 C,1 C,1 C,1 C,1 C,1 C,1

222222332221

2345 678910

Atom type

and number

of parents

Invariant

109

FIGURE 2.6 Atomic signature. (a) 1,8-Dimethyl-decahydronaphthalene, where carbon atoms

have been arbitrarily numbered. (b) Signature tree of atom 1. (c) Atom initial invariants.

Algorithms to Store and Retrieve Two-Dimensional (2D) Chemical Structures 57

tree has been constructed up to layer l, layer l +1 is constructed considering each

vertex y of layer l. Let z be a neighbor of y in G. Vertex z and edge [y,z] are added to

layer l +1 if the edges [y,z]or[z,y] are not already present in the previous layers of

the tree. To each vertex added to the tree, one associates an atom type and the initial

label or number of the corresponding atom. Note that a given atom number z may

appear several times in the tree (such as atom number 5 in Figure 2.6) since it can

be the neighbor of several atoms present in the previous layer. Having defined atom

signatures, we next explain how these signatures can be used to compute invariant

and ultimately canonized molecular graphs.

The approach taken to canonize atomic signatures is based on the classical Hopcroft

and Tarjan’s rooted tree canonization algorithm [51]. Let x be an atom of a molecular

graph G, and T(x), the corresponding signature tree. To each atom a one associates

an atom type and an invariant, inv(a). Invariants are integers no greater than N, the

total number of atoms. To each vertex v in T(x) one associates a corresponding atom,

atom(v), in graph G and an invariant, inv(v). Additionally, for each vertex of any layer

l, one can access its parents in layer l − 1 and its children in layer l +1.

Prior to running the algorithm, all the invariants are initialized. The initial invariant

of any atom a is computed from the atom type of a and the number of parents a has

in T(x). More precisely, a string of characters is compiled from the atom type and the

number of parents, and the string is converted into an integer following lexicographic

ordering. The integer is not greater than N since there are no more than N different

strings. Examples of initial invariants are given in Figure 2.6c.

After initialization, the first step of the algorithm is to compute the invariants

of the

vertices in T(x) from the atom invariants. The vertex invariants are com-

puted twice, first reading the tree layer by layer from the leaves to the root, and

then from the root to the leaves. Unlike the classical Hopcroft–Tarjan algorithm, the

tree must also be read from the root to the leaves because, in signature trees, some

vertices may have more than one parent; thus the invariants for these vertices may

be different depending on the invariants of their parents. We first examine the case

where the tree is read from the leaves to the root. Starting at the last layer, to each

vertex we associate the invariant of the corresponding atom. Duplicated invariants

are removed and all nonidentical invariants are sorted in decreasing order. The ver-

tex invariant becomes the order of the vertex in the sorted list. Going to the layer

above, to each vertex one assigns a vector composed of the invariant of the corre-

sponding atom and the invariants of the children of the vertex. Duplicated vectors

are removed, the remaining vectors are sorted in decreasing order, and the vertex

invariant becomes the order of the vertex in the sorted list. Note that these vertex

invariants range from 1 to N since there are no more than Nvertices in a layer.

The above procedure is repeated until the root is reached. The algorithm is then

run from the root to the leaves but this time for any vertex; the vector invariant is

composed of the invariant of the corresponding atom and the invariants of the parents

of the vertex. The Algorithm 2.4 is given below and is illustrated in Figure 2.7 for

1,8-dimethyl-decahydronaphthalene.

Once invariants have been computed for all vertices, each atom invariant is com-

piled from the invariant of all the vertices corresponding to the atom. Precisely, for