Фаулер М. Архитектура корпоративных программных приложений
Подождите немного. Документ загружается.


504 Часть II. Типовые решения
денежными объектами. Кроме того, все содержимое кошелька может быть переведено в
какую-либо одну валюту.
Операции умножения и деления еще более сложны, потому что их выполнение неми-
нуемо приводит к проблемам округления. При умножении денежных величин можно
воспользоваться обычными числами: например, чтобы подсчитать величину пятипро-
центного налога на сумму заказа, ее следует умножить на 0,05. Таким образом, выполне-
ние операций умножения над денежными объектами подразумевает умножение объекта
на скалярную величину, что не так сложно.
Настоящие проблемы округления возникают в ситуациях, когда заданную сумму де-
нег необходимо распределить между несколькими различными местами. В связи с этим
попробуйте решить простенькую задачку, предложенную Мэттью Фоммелем (Matthew
Foemmel). Предположим, у меня есть бизнес-правило, в соответствии с которым я дол-
жен положить имеющуюся сумму денег на два банковских счета: 70% суммы на первый
счет и 30% — на второй. Пусть эта сумма составляет 5 центов. В результате вычислений
я получаю, что на первый счет нужно положить 3,5 цента, а на второй — 1,5 цента. Если я
выполню стандартное округление до ближайшего целого числа, полтора цента превра-
тятся в два, а три с половиной — в четыре. Как видите, в сумме у меня появился лишний
цент. Если же я округлю полученные величины путем отбрасывания дробной части, то
получу 4 цента, т.е. потеряю один цент. Таким образом, я не могу применить к обеим ве-
личинам одну и ту же схему округления, потому что все универсальные схемы приводят к
потере или приобретению "лишних" центов.
Мне встречалось несколько вариантов решения данной проблемы.
• Наиболее распространенное решение — не обращать на это внимания (в конце
концов, речь идет о каком-то там центе). Тем не менее большинство банковских
клиентов были бы крайне возмущены подобной небрежностью по отношению к
своим деньгам.
• Вычислять сумму, которую нужно положить на последний счет, путем вычитания
из общей суммы денег тех сумм, которые были положены на все предыдущие сче
та. Это позволит избежать потери центов, однако в конце концов может привести
к накоплению на последнем счете довольно большого количества центов, которые
ему не принадлежат.
• Предоставить пользователям класса Money возможность самим выбирать схему
округления при вызове нужного метода. В этом случае программист может ука
зать, что 70% суммы следует округлить до следующего целого числа, а 30%
суммы— до предыдущего. Разумеется, подобный метод весьма неудобен, если
деньги нужно распределить не между двумя, а, скажем, между десятью счетами.
Кроме того, об указании схемы округления легко забыть. Иногда во избежание по
добных проблем метод умножения класса Money принудительно снабжают пара
метром округления. Это не только обяжет программиста выбрать схему округле
ния, но и напомнит ему о необходимости написания тестов. К сожалению, данный
подход весьма непрактичен при выполнении множества вычислений (например,
при подсчете величин налогов), использующих одну и ту же схему округления.
• Идеальное, на мой взгляд, решение — создать специальную функцию-распреде
литель. В качестве параметра этой функции будет передаваться список чисел, оп
ределяющих пропорцию, согласно которой необходимо распределить деньги

Глава 18. Базовые типовые решения 505
(например, aMoney.allocate ([7, 3])). По окончании выполнения функция-
распределитель будет возвращать список денежных значений. Чтобы гарантиро-
вать отсутствие лишних или утерянных центов, оставшиеся от округления центы
распределяются между всеми счетами псевдослучайным способом. Применение
функции-распределителя имеет свои недостатки: во-первых, о ней можно забыть,
а во-вторых, она не позволяет применить более четкие правила распределения ос-
тавшихся центов.
Описанные подходы касаются фундаментального различия между выполнением опе-
рации умножения для определения величины, пропорциональной исходной сумме
(например, налога на сумму заказа), или же для распределения исходной суммы по не-
скольким местам. Первую процедуру удобнее реализовать с помощью умножения, а вто-
рую — с помощью распределения. Таким образом, при выполнении умножения или де-
ления денежных величин необходимо тщательно следить за тем, для чего эта операция
применяется.
При необходимости объект Money можно снабдить методами, выполняющими пере-
расчет ИЗ ОДНОЙ ВаЛЮТЫ В Другую (например, методом aMoney.convertTo (Currency.
DOLLARS) ). Наиболее очевидный способ выполнения такого перерасчета— посмотреть
курс валют и умножить денежную величину на соответствующий коэффициент. К сожа-
лению, в некоторых ситуациях этот подход может не сработать. Правила перерасчета ос-
новных европейских валют подразумевают специфическое выполнение округлений, ко-
торое противоречит описанной выше простой схеме. В этом случае для инкапсуляции
алгоритма перерасчета следует создать отдельный объект-преобразователь.
Для сортировки денежных величин можно использовать операции сравнения.
При попытке сравнения значений, представленных в разных валютах, система может вы-
дать ошибку или же выполнить автоматический перерасчет величин в одну из валют.
Помимо всего прочего, типовое решение деньги может инкапсулировать в себе вы-
полнение отображения. Это позволяет отображать денежные значения в элементах
управления пользовательских интерфейсов и при печати отчетов так, как это делается в
реальной жизни. Кроме того, объект Money может включать в себя анализатор входной
строки, чтобы обеспечить механизм ввода, специфичный для конкретной валюты.
Для реализации подобного механизма можно воспользоваться библиотеками, прила-
гаемыми к вашей платформе. Сегодня все больше и больше платформ обеспечивают
поддержку глобализации, предоставляя специальные средства форматирования для ото-
бражения валют определенных стран.
Хранение денежных объектов в базе данных также чревато определенными пробле-
мами, поскольку базы данных (в отличие от своих производителей) не понимают всю
значимость денег. Наиболее очевидное решение — хранить денежные величины в виде
внедренного значения (Embedded Value, 288). В этом случае вместе с каждым денежным
значением будет сохраняться название соответствующей валюты, что может оказаться
крайне неудобным, например если все суммы на счете клиента указаны в фунтах. В по-
добных ситуациях название валюты лучше хранить где-нибудь в одном месте и изменить
код отображения на базу данных таким образом, чтобы при загрузке объектов соответст-
вующий преобразователь извлекал и название валюты, в которой ведется счет.

506 Часть II. Типовые решения
Назначение
Я применяю типовое решение деньги для выполнения практически всех числовых вы-
числений в объектно-ориентированных средах разработки. Основной аргумент в пользу
данного типового решения связан с необходимостью инкапсулировать обработку округ-
ления, что позволяет избежать большинства ошибок округления до фиксированного ко-
личества десятичных знаков. Еще одним преимуществом является возможность одно-
временного выполнения вычислений в нескольких валютах. Разумеется, наличие подоб-
ных объектов может сказаться на производительности, хотя я крайне редко слышал о
случаях, когда применение данного типового решения существенно снижало производи-
тельность приложения. Впрочем, даже тогда инкапсуляция денежных величин в отдель-
ных объектах значительно упрощала выполнение финансовых операций, ради чего стои-
ло пойти на определенные жертвы.
Пример: класс Money (Java)
Мэттью Фоммел и Мартин Фаулер
Реализуя класс Money, нужно решить, какой тип данных будет применяться для хра-
нения величины денежной суммы. Вы все еще убеждены в необходимости применения
действительного типа с плавающей точкой? Тогда попробуйте запустить приведенный
ниже код.
double val = 0.00;
for (int i = 0; i < 10; i++) val += 0.10;
System.out.println(val == 1.00);
Думаю, после выполнения этого простенького примера вы напрочь откажетесь от
применения чисел с плавающей точкой. Оставшиеся альтернативы включают в себя чис-
ла с фиксированной точкой и целые числа. В Java им соответствуют типы данных Big-
Decimal, Biginteger и long. Использование целочисленных типов значительно упро-
щает выполнение внутренних арифметических операций. Кроме того, long является
стандартным типом данных, а значит, существенно повышает читабельность математи-
ческих выражений.
class Money...
private long amount; private
Currency currency;
В данном примере я использую целочисленный тип данных, поэтому денежные вели-
чины необходимо выражать в наименьших единицах текущей валюты (для простоты я
назвал их центами). При использовании типа long для операций над очень большими
числами может возникнуть ошибка переполнения. Таким образом, если вам понадобится
оперировать суммами наподобие 92 233 720 368 547 758,09 доллара, подумайте о приме-
нении типа Biginteger.
Чтобы облегчить создание объектов, предоставим несколько конструкторов, прини-
мающих в качестве аргумента различные типы данных.

Глава 18. Базовые типовые решения 507
public Money(double amount, Currency currency) {
this.currency = currency; this.amount =
Math.round(amount * centFactor());
public Money(long amount, Currency currency) {
this.currency = currency;
this.amount = amount * centFactor(); } private static final
int[] cents = new int[] { 1, 10, 100,
1000 }; private int
centFactor() {
return cents[currency.getDefaultFractionDigits() ] ; }
Денежные единицы различных валют делятся на разное количество более мелких
единиц. В версии Java 1.4 количество элементарных единиц, на которые делится основ-
ная денежная единица, определяется классом Currency. Чтобы узнать, сколько элемен-
тарных единиц (например, центов) содержится в сумме, выраженной в основных де-
нежных единицах (например, в долларах), ее нужно умножить на 10 в соответствующей
степени. Впрочем, выполнение подобных операций в Java настолько неудобно, что
вместо возведения в степень гораздо проще (и быстрее) воспользоваться массивом. Ра-
зумеется, нужно быть морально готовым к тому, что наше приложение откажется рабо-
тать с гипотетическими валютами, в которых основная денежная единица состоит из
10 000 "копеек".
Хотя в большинстве случаев арифметические операции будут выполняться над сами-
ми объектами Money, нам может понадобиться осуществить доступ к содержимому по-
следних.
class Money...
public BigDecimal amount() {
return BigDecimal.valueOf(amount,
currency.getDefaultFractionDigits() ) ;
} public Currency currency!) {
return currency;
}
He забывайте: к использованию функций доступа следует обращаться только в самых
крайних случаях. Практически всегда к содержимому объекта можно добраться более
удачным способом, не нарушая его инкапсуляции. В качестве примера можно привести
отображение на базу данных, рассмотренное в разделе, посвященном внедренному значе-
нию (см. главу 12).
Чтобы облегчить создание денежных объектов в определенной часто используемой
валюте (например, в долларах), можно написать вспомогательный конструктор.
class Money...
public static Money dollars(double amount) {
return new Money(amount, Currency.USD);
}

508 Часть II. Типовые решения
Поскольку деньги являются о&ьектом-значением (Value Object, 500), необходимо опре-
делить метод проверки на равенство.
class Money...
public boolean equals(Object other) {
return (other instanceof Money) S& equals((Money)other); }
public boolean equals(Money other) {
return currency.equals(other.currency) && (amount ==
other.amount); }
Там, где есть метод проверки на равенство, не обойтись без хэширования.
class Money...
public int hashCodeO (
return (int) (amount
Л
(amount >» 32));
}
Пришло время определить арифметические операции, совершаемые над объектами
Money. Начнем со сложения и вычитания.
class Money...
public Money add(Money other) {
assertSameCurrencyAs(other); return
newMoney(amount + other.amount);
}
private void assertSameCurrencyAs(Money arg) {
Assert.equals("money math mismatch", currency,
arg.currency);
}
private Money newMoney(long amount)
{
Money money = new Money();
money.currency = this.currency;
money.amount = amount;
return money; }
Обратите внимание на использование закрытого метода-фабрики NewMoney, который
не выполняет привычное преобразование долларов в центы. Этот метод будет несколько
раз фигурировать во внутреннем коде объекта Money.
Имея метод сложения, определить вычитание совсем несложно.
class Money.. .
public Money subtract(Money other) {
assertSameCurrencyAs(other) ;
return newMoney(amount - other.amount);
}

Глава 18. Базовые типовые решения 509
В качестве базового метода сравнения будет выступать метод compareTo.
class Money...
public int compareTo(Object other) {
return compareTo((Money) other) ; }
public int compareTo(Money other) {
assertSameCurrencyAs(other) ;
if (amount < other.amount) return -1;
else if (amount == other.amount) return 0;
else return 1;
}
Это практически все, что можно выжать из классов Java в настоящее время. Тем не
менее можно немного повысить читабельность кода, реализовав еще несколько методов
сравнения наподобие приведенного ниже.
class Money...
public boolean greaterThan(Money other) {
return (compareTo(other) > 0) ;
}
Теперь можно взяться и за умножение. В данном примере воспользуемся стандарт-
ным режимом округления, однако при необходимости можно определить какой-нибудь
другой режим.
class Money...
public Money multiply(double amount) {
return multiply(new BigDecimal(amount));
}
public Money multiply(BigDecimal amount) {
return multiply(amount, BigDecimal.ROUND_HALF_EVEN);
}
public Money multiply (BigDecimal amount, int roundingMode) {
return new Money(amount().multiply(amount), currency,
roundingMode); }
Чтобы распределить сумму денег между несколькими счетами, не потеряв при этом
ни цента, понадобится реализовать метод распределения. Самая простая схема распреде-
ления предполагает, что на все счета будут положены одинаковые (или почти одинако-
вые) денежные суммы.
class Money...
public Money[] allocate(int n) {
Money lowResult = newMoney(amount / n);
Money highResult = newMoney(lowResult.amount + 1) ;
Money[] results = new Money[n];

510 Часть II. Типовые решения
int remainder = (int) amount % n;
for (int i = 0; i < remainder; i++) results [i] =
highResult;
for (int i = remainder; i < n; i++) results [i] =
lowResult;
return results; }
Более сложный алгоритм распределения может поделить деньги в любой заданной
пропорции.
class Money...
public Money!] allocate(long[] ratios) {
long total = 0;
for (int i = 0; i < ratios.length; i++) total +=
ratios[i] ;
long remainder = amount;
Money[] results = new Money[ratios.length];
for (int i = 0; i < results.length; i++) {
results [i] = newMoney(amount * ratios[i] / total);
remainder -= results[i].amount; } for (int i = 0; i <
remainder; i++) {
results[i].amount++;
}
return results; }
Данный алгоритм можно применить для решения задачки Мэтгью Фоммела (Matthew
Foemmel).
class Money...
public void testAllocate2() {
long[] allocation = {3,7};
Money[] result = Money.dollars(0.05).allocate(allocation);
assertEquals(Money.dollars(0.02), result[0]);
assertEquals(Money.dollars(0.03), result[1]);
}
Значения NULL — настоящий бич объектно-ориентированных приложений. Потенци-
альное наличие таких значений напрочь лишает разработчика возможности воспользо-
ваться преимуществами полиморфизма. Обычно методу можно передавать ссылки на
переменные или же значения заданных типов, не беспокоясь о том, принадлежит ли пе-
реданное значение к указанному типу или же к производному классу. В строго типизиро-
ванных языках проверку на правильность вызова можно проводить еще на этапе компи-
ляции. К сожалению, если передаваемая переменная имеет значение NULL, при попытке
доступа к последнему вы совершите ошибку времени выполнения и получите не более
чем красивую и весьма "дружелюбную" трассировку стека.
Если переменная может принимать значение NULL, следует позаботиться о реализа-
ции проверки на наличие последнего, чтобы при его обнаружении приложение выполня-
ло некие особые действия. Зачастую "особые действия" одинаковы во многих контек-
стах, что, несомненно, приводит к необходимости повторения одних и тех же фрагментов
кода в различных местах приложения. Итак, снова дублирование?
Наличие значений NULL — наиболее распространенный, но далеко не единственный
пример подобных проблем. Большинство математических приложений связаны с обра-
боткой бесконечности. Сложение бесконечных величин выполняется по иным правилам,
чем сложение обычных действительных чисел. В качестве еще одного примера могу при-
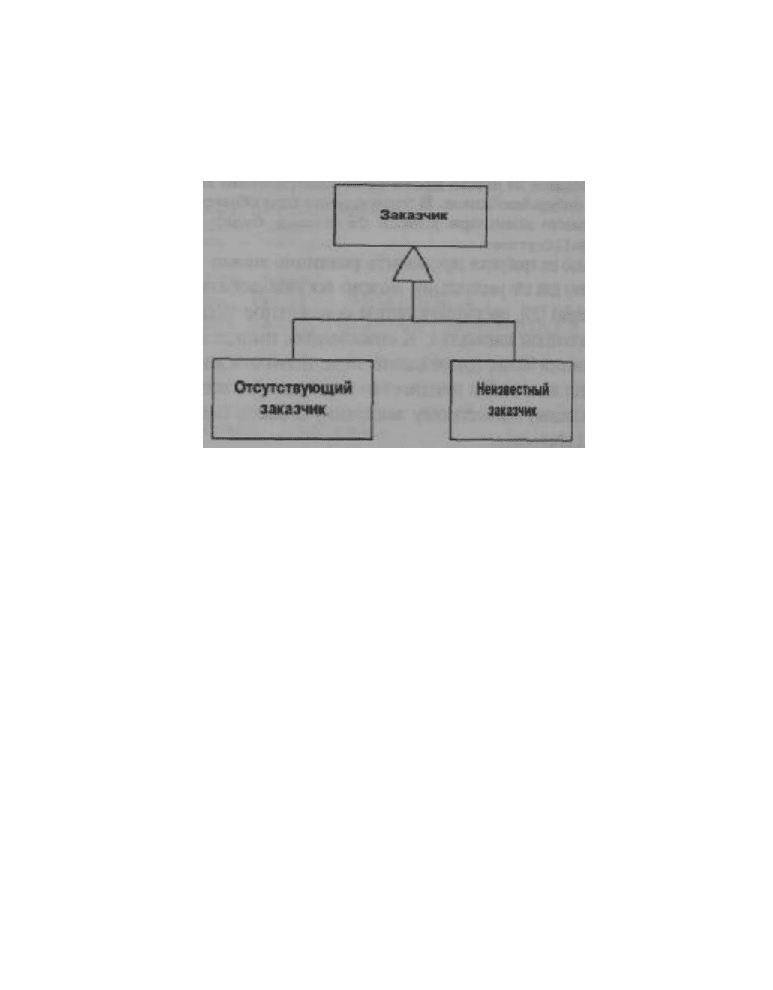
вести случай из моего раннего опыта работы с бизнес-приложениями, касающийся обра-
ботки неизвестного или не полностью известного заказчика (мы называли его "захват-
чиком"). Все описанные выше ситуации имеют одну общую особенность: они предпо-
лагают изменение обычного поведения объектов данного типа.
Вместо того чтобы при возникновении особых ситуаций возвращать значение NULL
или вообще что-нибудь непонятное, можно воспользоваться типовым решением частный
случай. Последнее возвращает специальный объект с тем интерфейсом, который ожидает
увидеть вызывающий метод.
Глава 18. Базовые типовые решения 511
Частный случай (Special Case)
Производный класс, описывающий поведение объекта
в особых ситуациях

512 Часть II. Типовые решения
Принцип действия
Основная идея данного типового решения состоит в том, чтобы создать производный
класс для обработки частных, особых случаев. Таким образом, чтобы избежать проверки
объекта Customer на наличие значений NULL, можно создать объект NullCustomer. По-
следний будет переопределять все методы объекта Customer, чтобы при возникновении
особой ситуации приложение не начало вести себя совершенно непредсказуемым обра-
зом, а выполнило что-нибудь безобидное. В этом случае при обнаружении значения NULL
вызывающий метод вместо экземпляра класса Customer будет возвращать экземпляр
производного класса NullCustomer.
Обычно приложению не требуется проводить различие между экземплярами объекта
NullCustomer, поэтому для его реализации можно воспользоваться типовым решением
приспособленец (Flyweight) [20], предполагающим совместное использование одного эк-
земпляра объекта в нескольких контекстах. К сожалению, иногда этот прием не срабаты-
вает. В уже упоминавшемся бизнес-приложении подсчитывать долг заказчика следовало
всегда — даже когда этот заказчик был неизвестен и сведений о его заказе практически не
было. В этом случае каждому неизвестному заказчику должен был соответствовать свой
экземпляр объекта NullCustomer.
Значения NULL могут иметь разную природу. Наличие объекта NullCustomer может
означать, что заказчика нет или же что заказчик есть, но мы не знаем, кто он. В подобных
случаях вместо применения общего объекта NullCustomer рекомендуется описать от-
дельные частные случаи для отсутствующего заказчика (например, MissingCustomer) и
для неизвестного заказчика (например, UnknownCustomer).
Нередки ситуации, когда при переопределении методов в частном случае последний
возвращает еще один частный случай, например при запросе последнего счета неизвест-
ного покупателя соответствующий метод объекта UnknownCustomer может возвратить
объект UnknownBill.
Определение арифметических операций над числами с плавающей точкой, приведен-
ное в стандарте ШЕЕ 754, содержит хорошие примеры частных случаев, касающихся об-
работки положительных бесконечных величин, отрицательных бесконечных величин и
значений типа NaN (not-a-number — не число). При попытке деления на нуль подобные
системы не генерируют исключение, а возвращают значение типа NaN, которое может
участвовать в выполнении арифметических операций наравне с обычными числами.
Назначение
Типовое решение частный случай следует применять для описания повторяющегося
поведения, связанного с обработкой значений NULL ИЛИ других особых ситуаций после
выполнения соответствующих проверок на их наличие.
Дополнительные источники информации
Я еще не встречал описания частного случая в виде отдельного типового решения. Тем
не менее в [40] содержится описание типового решения null-объект (Null Object),
которое — надеюсь, вы простите мне небольшой каламбур— можно рассматривать как
частный случай частного случая.

Глава 18. Базовые типовые решения 513
Пример: объект NullEmpIoyee (C#)
Ниже приведен небольшой пример использования частного случая для обработки
значений NULL.
У нас есть обычный класс Employee,
class Employee...
public virtual String Name {
get {return _name;}
set {_name = value;}
}
private String _name; public virtual
Decimal GrossToDate {
get {return calculateGrossFromPeriod(O);} }
public virtual Contract Contract {
get {return _contract;} }
private Contract __contract;
Поведение этого объекта может быть переопределено методами класса NullEm-
ployee.
class NullEmpIoyee : Employee, INull...
public
override String Name {
get
{return "Null Employee";}
set
{}
}
public
override Decimal GrossToDate {
get
{return Om;}
}
public
override Contract Contract {
get
{return Contract.NULL;}
}
Обратите внимание, что при попытке извлечения значения контракта из объекта
NullEmpIoyee мы получаем значение NULL.
Приведенные выше переменные позволяют избежать реализации множества прове-
рок на наличие значений NULL, если все эти значения имеют одну и ту же природу.
По умолчанию повторяющиеся значения NULL обрабатываются объектом NullEmpIoyee.
Кроме того, проверку на наличие значений NULL МОЖНО ВЫПОЛНИТЬ И ЯВНО, снабдив объ-
ект Employee методом isNull или проверив тип объекта на предмет реализации соот-
ветствующего опознавательного интерфейса (marker interface).
