Evans L.C. An Introduction to Stochastic Differential Equations
Подождите немного. Документ загружается.


DEFINITION. Let W(·)beann-dimensional Brownian motion and let B : R
n
×[0,T] →
M
n×n
be a C
1
function such that
E
T
0
|B(W,t)|
2
dt
< ∞.
Then we define
T
0
B(W,t) ◦ dW := lim
|P
n
|→0
m
n
−1
k=0
B
W(t
n
k+1
)+W(t
n
k
)
2
,t
n
k
(W(t
n
k+1
) − W(t
n
k
)).
It can be shown that this limit exists in L
2
(Ω).
A CONVERSION FORMULA. Remember that Itˆo’s integral can be computed this
way:
T
0
B(W,t) dW = lim
|P
n
|→0
m
n
−1
k=0
B(W(t
n
k
),t
n
k
)(W(t
n
k+1
) − W(t
n
k
)).
This is in general not equal to the Stratonovich integral, but there is a conversion formula
(38)
)
T
0
B(W,t) ◦ dW
*
i
=
)
T
0
B(W,t) dW
*
i
+
1
2
T
0
n
j=1
∂b
ij
∂x
j
(W,t) dt,
for i =1,...,n. Here v
i
means the i
th
–component of the vector function v. This formula
is proved by noting
T
0
B(W,t) ◦ dW −
T
0
B(W,t) dW
= lim
|P
n
|→0
m
n
−1
k=0
%
B
W(t
n
k+1
)+W(t
n
k
)
2
,t
n
k
− B(W(t
n
k
),t
n
k
)
&
· (W(t
n
k+1
) − W(t
n
k
))
and using the Mean Value Theorem plus some usual methods for evaluating the limit. We
omit details.
Special case. If n = 1, then
T
0
b(W, t) ◦ dW =
T
0
b(W, t) dW +
1
2
T
0
∂b
∂x
(W, t) dt.
Assume now B : R
n
×[0,T] → M
n×m
and W(·)isanm-dimensional Brownian motion.
We make this informal
121

DEFINITION. If X(·) is a stochastic process with values in R
n
, we define
T
0
B(X,t) ◦ dW := lim
|P
n
|→0
m
n
−1
k=0
B
X(t
n
k+1
)+X(t
n
k
)
2
,t
n
k
(W(t
n
k+1
) − W(t
n
k
)),
provided this limit exists in L
2
(Ω) for all sequences of partitions P
n
, with |P
n
|→0.
3. Stratonovich chain rule.
DEFINITION. Suppose that the process X(·) solves the Stratonovich integral equation
X(t)=X(0) +
t
0
b(X,s) ds +
t
0
B(X,s) ◦ dW (0 ≤ t ≤ T )
for b : R
n
× [0,T] → R
n
and B : R
n
× [0,T] → M
n×m
. We then write
dX = b(X,t)dt + B(X,t) ◦ dW,
the second term on the right being the Stratonovich stochastic differential.
THEOREM (Stratonovich chain rule). Assume
dX = b(X,t)dt + B(X,t) ◦ dW
and suppose u : R
n
× [0,T] → R is smooth. Define
Y (t):=u(X(t),t).
Then
dY =
∂u
∂t
dt +
n
i=1
∂u
∂x
i
◦ dX
i
=
∂u
∂t
+
n
i=1
∂u
∂x
i
b
i
dt +
n
i=1
m
k=1
∂u
∂x
i
b
ik
◦ dW
k
.
Thus the ordinary chain rule holds for Stratonovich stochastic differentials, and there is
no additional term involving
∂
2
u
∂x
i
∂x
j
as there is for Itˆo’s formula. We omit the proof, which
is similar to that for the Itˆo rule. The main difference is that we make use of the formula
T
0
W ◦ dW =
1
2
W
2
(T ) in the approximations.
122

More discussion. Next let us return to the motivational example we began with. We
have seen that if the differential equation (33) is interpreted to mean
dX = d(t)Xdt + f(t)XdW (Itˆo’s sense),
X(0) = X
0
,
then
X(t)=X
0
e
t
0
d(s)−
1
2
f
2
(s) ds+
t
0
f(s) dW
.
However, if we interpret (33) to mean
dX = d(t)Xdt + f(t)X ◦dW (Stratonovich’s sense)
X(0) = X
0
,
the solution is
˜
X(t)=X
0
e
t
0
d(s) ds+
t
0
f(s) dW
,
as is easily checked using the Stratonovich calculus described above.
This solution
˜
X(·) is also the solution obtained by approximating the “white noise” ξ(·)
by smooth processes ξ
k
(·) and passing to limits. This suggests that interpreting (16) and
similar formal random differential equations in the Stratonovich sense will provide solutions
which are stable with respect to perturbations in the random terms. This is indeed the
case: See the articles [S1-2] by Sussmann.
Note also that these considerations clarify a bit the problems of interpreting mathemat-
ically the formal random differential equation (33), but do not say which interpretation is
physically correct. This is a question of modeling and is not, strictly speaking, a mathe-
matical issue.
CONVERSION RULES FOR SDE.
Let W(·)beanm-dimensional Wiener process and suppose b : R
n
× [0,T] → R
n
,
B : R
n
× [0,T] → M
n×m
satisfy the hypotheses of the basic existence and uniqueness
theorem. Then X(·) solves the Itˆo stochastic differential equation
dX = b(X,t)dt + B(X,t)dW
X(0) = X
0
if and only if X(·) solves the Stratonovich stochastic differential equation
dX =
+
b(X,t) −
1
2
c(X,t)
,
dt + B(X,t) ◦ dW
X(0) = X
0
,
for
c
i
(x, t)=
m
k=1
n
j=1
∂b
ik
∂x
j
(x, t)b
jk
(x, t)(1≤ i ≤ n).
123

A special case. For m = n = 1, this says
dX = b(X)dt + σ(X)dW
if and only if
dX =(b(X) −
1
2
σ
(X)σ(X))dt + σ(X) ◦ dW.
4. Summary We conclude these lectures by summarizing the advantages of each
definition of the stochastic integral:
Advantages of Itˆo integral
1. Simple formulas: E
t
0
GdW
=0,E
t
0
GdW
2
= E
t
0
G
2
dt
.
2. I(t)=
t
0
GdW is a martingale.
Advantages of Stratonovich integral
1. Ordinary chain rule holds.
2. Solutions of stochastic differential equations interpreted in Stratonovich sense are
stable with respect to changes in random terms.
124
APPENDICES
Appendix A: Proof of Laplace–De Moivre Theorem (from §G in Chapter 2)
Proof. 1. Set S
∗
n
:=
S
n
−np
√
npq
, this being a random variable taking on the value x
k
=
k−np
√
npq
(k =0,...,n) with probability p
n
(k)=
n
k
p
k
q
n−k
.
Look at the interval
-
−np
√
npq
,
nq
√
npq
.
. The points x
k
divide this interval into n subintervals
of length
h :=
1
√
npq
.
Now if n goes to ∞, and at the same time k changes so that |x
k
| is bounded, then
k = np + x
k
√
npq →∞
and
n − k = nq − x
k
√
npq →∞.
2. We recall next Stirling’s formula, which says says
n!=e
−n
n
n
√
2πn (1 + o(1)) as n →∞,
where “o(1)” denotes a term which goes to 0 as n →∞. (See Mermin [M] for a nice
discussion.) Hence as n →∞
(1)
p
n
(k)=
n
k
p
k
q
n−k
=
n!
k!(n − k)!
p
k
q
n−k
=
e
−n
n
n
√
2πnp
k
q
n−k
e
−k
k
k
√
2πke
−(n−k)
(n − k)
(n−k)
2π(n − k)
(1 + o(1))
=
1
√
2π
/
n
k(n − k)
np
k
k
nq
n − k
n−k
(1 + o(1)).
3. Observe next that if x = x
k
=
k−np
√
npq
, then
1+
/
q
np
x =1+
/
q
np
k − np
√
npq
=
k
np
and
1 −
/
p
nq
x =
n − k
nq
.
125
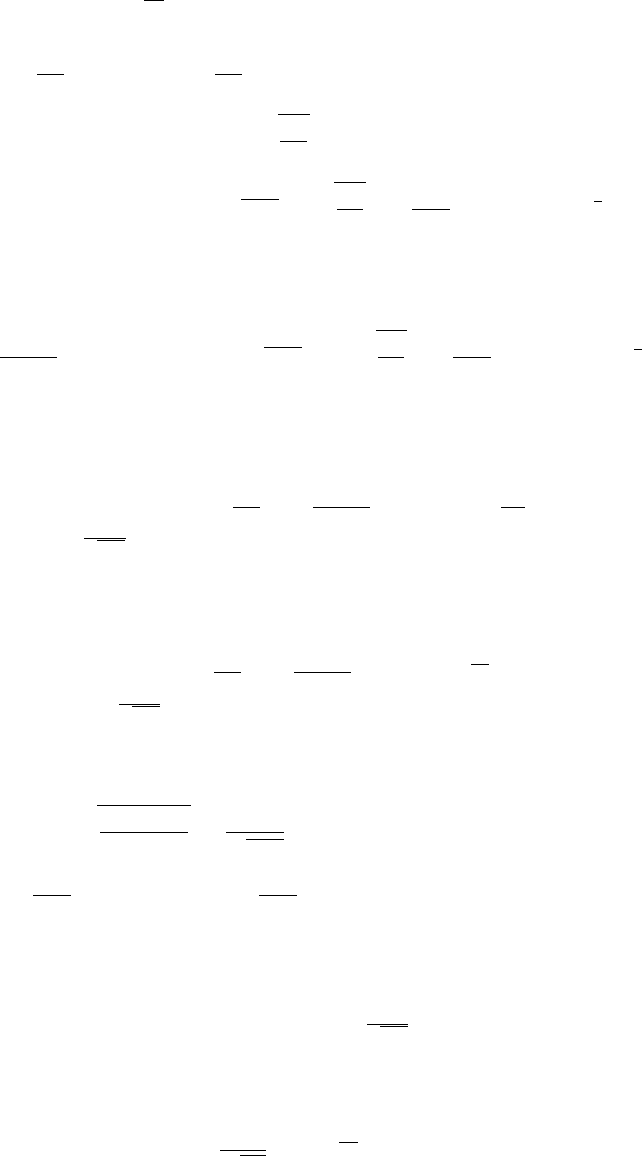
Note also log(1 ± y)=±y −
y
2
2
+ O(y
3
)asy → 0. Hence
log
np
k
k
= −k log
k
np
= −k log
1+
/
q
np
x
= −(np + x
√
npq)
/
q
np
x −
q
2np
x
2
+ O
n
−
1
2
.
Similarly,
log
nq
n − k
n−k
= −(nq − x
√
npq)
−
/
p
nq
x −
p
2nq
x
2
+ O
n
−
1
2
.
Add these expressions and simplify, to discover
lim
n→∞
k−np
√
npq
→x
log
np
k
k
nq
n − k
n−k
= −
x
2
2
.
Consequently
(2) lim
n→∞
k−np
√
npq
→x
np
k
k
nq
n − k
n−k
= e
−
x
2
2
.
4. Finally, observe
(3)
/
n
k(n − k)
=
1
√
npq
(1 + o(1)) = h(1 + o(1)),
since k = np + x
√
npq, n − k = nq −x
√
npq.
Now
P (a ≤ S
∗
n
≤ b)=
a≤x
k
≤b
x
k
=
k−np
√
npq
p
n
(k)
for a<b. In view of (1) − (3), the latter expression is a Riemann sum approximation as
n →∞of the integral
1
√
2π
b
a
e
−
x
2
2
dx.
Appendix B: Proof of discrete martingale inequalities (from §I in Chapter 2)
126

Proof. 1. Define
A
k
:=
k−1
j=1
{X
j
≤ λ}∩{X
k
>λ} (k =1,...,n).
Then
A :=
max
1≤k≤n
X
k
>λ
"
=
n
k=1
A
k
disjoint union
.
Since λP (A
k
) ≤
A
k
X
k
dP ,wehave
(4) λP (A)=λ
n
k=1
P (A
k
) ≤
n
k=1
E(χ
A
k
X
k
).
Therefore
E(X
+
n
) ≥
n
k=1
E(X
+
n
χ
A
k
)
=
n
k=1
E(E(X
+
n
χ
A
k
|X
1
,...,X
k
))
=
n
k=1
E(χ
A
k
E(X
+
n
|X
1
,...,X
k
))
≥
n
k=1
E(χ
A
k
E(X
n
|X
1
,...,X
k
))
≥
n
k=1
E(χ
A
k
X
k
) by the submartingale property
≥ λP (A) by (4).
2. Notice next that the proof above in fact demonstrates
λP
max
1≤k≤n
X
k
>λ
≤
{
max
1≤k≤n
X
k
>λ
}
X
+
n
dP.
Apply this to the submartingale |X
k
|:
(5) λP (X>λ) ≤
{X>λ}
YdP,
127

for X := max
1≤k≤n
|X
k
|, Y := |X
n
|. Now take some 1 <p<∞. Then
E(|X|
p
)=−
∞
0
λ
p
dP (λ) for P (λ):=P (X>λ)
= p
∞
0
λ
p−1
P (λ) dλ
≤ p
∞
0
λ
p−1
1
λ
{X>λ}
YdP
dλ by (5)
= p
Ω
Y
X
0
λ
p−2
dλ
dP
=
p
p − 1
Ω
YX
p−1
dP
≤
p
p − 1
Ω
Y
p
dP
1/p
Ω
X
p
dP
1−1/p
.
Appendix C: Proof of continuity of indefinite Itˆo integral (from §C in Chapter
4)
Proof. We will assume assertion (i) of the Theorem in §C of Chapter 4, which states that
the indefinite integral I(·) is a martingale.
There exist step processes G
n
∈ L
2
(0,T), such that
E
T
0
(G
n
− G)
2
dt
→ 0.
Write I
n
(t):=
t
0
G
n
dW , for 0 ≤ t ≤ T .IfG
n
(s) ≡ G
n
k
for t
n
k
≤ s<t
n
k+1
, then
I
n
(t)=
k−1
i=0
G
n
i
(W (t
n
i+1
) − W (t
n
i
)) + G
n
k
(W (t) − W (t
n
k
))
for t
n
k
≤ t<t
n
k+1
. Therefore I
n
(·) has continuous sample paths a.s., since Brownian
motion does. Since I
n
(·) is a martingale, it follows that |I
n
− I
m
|
2
is a submartingale.
The martingale inequality now implies
P
sup
0≤t≤T
|I
n
(t) − I
m
(t)| >ε
= P
sup
0≤t≤T
|I
n
(t) − I
m
(t)|
2
>ε
2
≤
1
ε
2
E(|I
n
(T ) − I
m
(T )|
2
)
=
1
ε
2
E
T
0
|G
n
− G
m
|
2
dt
.
128

Choose ε =
1
2
k
. Then there exists n
k
such that
P
sup
0≤t≤T
|I
n
(t) − I
m
(t)| >
1
2
k
≤ 2
2k
E
T
0
|G
n
(t) − G
m
(t)|
2
dt
≤
1
k
2
for m, n ≥ n
k
.
We may assume n
k+1
≥ n
k
≥ n
k−1
≥ ..., and n
k
→∞. Let
A
k
:=
sup
0≤t≤T
|I
n
k
(t) − I
n
k+1
(t)| >
1
2
k
"
.
Then
P (A
k
) ≤
1
k
2
.
Thus by the Borel–Cantelli Lemma, P (A
k
i.o.) = 0; which is to say, for almost all ω
sup
0≤t≤T
|I
n
k
(t, ω) − I
n
k+1
(t, ω)|≤
1
2
k
provided k ≥ k
0
(ω).
Hence I
n
k
(·,ω) converges uniformly on [0,T] for almost every ω, and therefore J(t, ω):=
lim
k→∞
I
n
k
(t, ω) is continuous for amost every ω.AsI
n
(t) → I(t)inL
2
(Ω) for all 0 ≤
t ≤ T , we deduce as well that J(t)=I(t) amost every for all 0 ≤ t ≤ T . In other words,
J(·) is a version of I(·). Since for almost every ω, J(·,ω) is the uniform limit of continuous
functions, J(·) has continuous sample paths a.s.
129

EXERCISES
(1) Show, using the formal manipulations for Itˆo’s formula discussed in Chapter 1, that
Y (t):=e
W (t)−
t
2
solves the stochastic differential equation
dY = YdW,
Y (0)=1.
(Hint: If X(t):=W (t) −
t
2
, then dX = −
dt
2
+ dW .)
(2) Show that
P (t)=p
0
e
σW(t)+
µ−
σ
2
2
t
,
solves
dP = µP dt + σP dW,
P (0) = p
0
.
(3) Let Ω be any set and A any collection of subsets of Ω. Show that there exists a
unique smallest σ-algebra U of subsets of Ω containing A. We call U the σ-algebra
generated by A.
(Hint: Take the intersection of all the σ-algebras containing A.)
(4) Let X =
k
i=1
a
i
χ
A
i
be a simple random variable, where the real numbers a
i
are
distinct, the events A
i
are pairwise disjoint, and Ω = ∪
k
i=1
A
i
. Let U(X) be the
σ-algebra generated by X.
(i) Describe precisely which sets are in U(X).
(ii) Suppose the random variable Y is U(X)-measurable. Show that Y is constant
on each set A
i
.
(iii) Show that therefore Y can be written as a function of X.
(5) Verify:
∞
−∞
e
−x
2
dx =
√
π,
1
√
2πσ
2
∞
−∞
xe
−
(x−m)
2
2σ
2
dx = m,
1
√
2πσ
2
∞
−∞
(x − m)
2
e
−
(x−m)
2
2σ
2
dx = σ
2
.
(6) (i) Suppose A and B are independent events in some probability space. Show that
A
c
and B are independent. Likewise, show that A
c
and B
c
are independent.
130
