Дворецкий С.И., Кормильцин Г.С., Калинин В.Ф. Основы проектирования химических производств

Подождите немного. Документ загружается.

В ChemCAD широко представлены модули для осуществления проектного и поверочного расчетов

кожухотрубчатых теплообменников, колонных аппаратов (тарельчатых и насадочных колонн ректифи-

кации и абсорбции нефтяных смесей, хемосорбции и др.), химических реакторов (идеального вытесне-

ния (RFR) и смешения (CSTR)), аппаратов высокого давления, трубопроводов, нормально сужающих

устройств (диафрагм) и регулирующих клапанов.

В ChemCAD имеются также средства для исследования и оптимизации статических и динамических

режимов функционирования как отдельных химико-технологических аппаратов, так и всей химико-

технологической схемы; чувствительности выходных переменных этих аппаратов по отношению к

входным переменным и возмущающим воздействиям.

4.6.2. ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПРОСТЕЙШИХ

ТИПОВЫХ ПРОЦЕССОВ БИО- И ХИМИЧЕСКОЙ ТЕХНОЛОГИИ

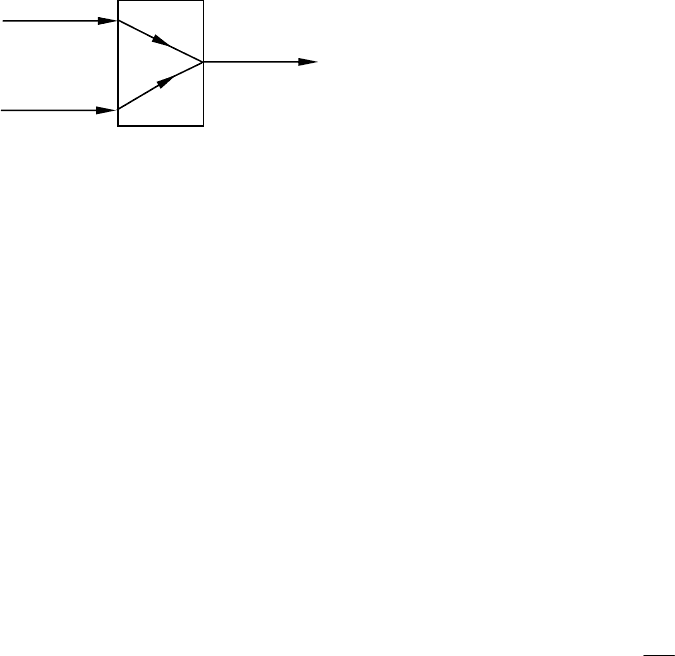
1. Модель процесса смешения потоков (рис. 47). Пусть в смеситель поступают два потока ве-

ществ, характеризующихся расходом

G , вектором концентраций веществ

и температурой

t .

Рис. 47. Структурная схема

смесителя потоков

Исходные данные:

концентрации

веществ

во входных потоках, рас-

ходы

G и

G и температу-

ры

t и

t входных пото-

ков.

Требуется построить

математическую модель,

позволяющую по исход-

ным данным рас-

считывать концентрации

c веществ и температуру

потока на выходе из смесителя.

Примем следующие допущения: 1) внутри аппарата реализуется режим идеального смешения и от-

сутствуют источники (стоки) вещества и теплоты; 2) удельные теплоемкости компонентов j-го потока в

зависимости от температуры

рассчитываются по формуле

jijijiiipj

tetdtbac +++= ,

где −

iiii

edba ,,, эмпирические коэффициенты, найденные для каждого i-го вещества.

Составим общее уравнение материального баланса при смешении двух потоков веществ в смесите-

ле и уравнения покомпонентного материального баланса:

,,1,0

2,21,1

miGcGcGc

GGG

iii

==−+

=−+

где

−

iii

ccc ,,

,2,1

массовые доли i-го вещества в потоках;

−

m число веществ в потоке.

Из последнего балансового уравнения можно рассчитать концентрации

c веществ на выходе из

смесителя

./)(

2,21,1

GGcGcc

iii

Далее составим уравнение теплового баланса для смесителя:

222111

−

tGctGctGc

ppp

где

−

удельная теплоемкость потока рассчитывается по формуле

111

t,G,c

222

t,G,c

.2,1,

∑

jccc

ipjpj

Из последнего балансового уравнения можно рассчитать температуру выходного потока

)./()(

222111

GctGctGct

ppp

Обратим внимание на нелинейность последнего уравнения, поскольку удельная теплоемкость вы-

ходного потока нелинейным образом зависит от температуры. Для его решения можно воспользоваться

методом простой итерации:

,))(/())()((

)(

22221111

)1(

GtctGtctGtct

ppp

ν+ν

где

−=ν ...,2,1,0

номер итерации.

В качестве условия окончания итерационного процесса (счета) можно использовать следующее ус-

ловие ,

)()1(

ε≤−

ν+ν

tt а в качестве начального приближения принять

.2/)(

)0(

ttt +=

2. Модель процесса теплообмена, осуществляемого в кожухотрубчатом теплообменнике (рис.

48). В трубном пространстве одноходового кожухотрубчатого теплообменника охлаждается жидкость

от температуры

t до температуры

. Охлаждающая жидкость (хладагент) проходит противотоком по

межтрубному пространству с расходом

G и начальной температурой

t .

Исходные данные: поверхность

теплообмена кожухотрубчатого теплообменника, коэффициенты

теплоотдачи

α и

α в трубном и межтрубном пространствах, толщина

, теплопроводность

стенки

и слоев загрязнений, ni ,1= ; расход G , начальная и конечные

Рис. 48. Структурная схема теплообменника

температуры

t и

t , удельные теплоемкости

cс охлаждаемой жидкости и хладагента, расход

G и начальная температура

t хладагента.

Требуется построить математическую модель, позволяющую рассчитывать температуру хладагента

t на выходе из теплообменника.

Примем следующие допущения: 1) теплопередача не сопровождается изменением агрегатного со-

стояния теплоносителей; 2) схема движения теплоносителей – противоток; 3) потери теплоты в окру-

жающее пространство не учитываются.

Составим общее уравнение теплового баланса для кожухотрубчатого теплообменника:

.0)()(

xxxкн

=−−− ttGсttGc

Из последнего уравнения можно выразить величину

t :

нк

GcGc

−

−=

,, ctG

Запишем теперь уравнение теплового баланса с учетом процесса теплопередачи через стенки труб

теплообменника:

[]

)/()(ln

)()(

)(

ткн

−−

−−−

−−

tttt

FKttGc

Если теперь в последнее уравнение подставить

t , то с учетом обозначений

)/(),/(

т2xx1

GcFKGcGс

ppp

=χ=χ

получим

))1((exp

1))1((exp

)(

112

xн

χ−χ−χ

−χ−χ

χ−+= tttt

Коэффициент теплопередачи

K рассчитывают по формуле

∑

α+λδ+α

/1//1

где

−αα

, коэффициенты теплоотдачи в трубном и межтрубном пространствах

[]

КВт/м

⋅

;

–

толщина и теплопроводность стенки и слоев загрязнений,

ni ,1= ;

[

]

КВт/м~

⋅

Значения коэффициентов теплоотдачи зависят от гидродинамической и тепловой обстановки около

теплообменной поверхности и в общем случае определяются на основе экспериментальных исследований,

обобщаемых в виде корреляционных соотношений между критериями подобия: Нуссельта, Пекле, Пран-

дтля, Рейнольдса, Галилея, Грасгофа [52].

3. Модель периодического процесса растворения смеси полидисперсных частиц [53]. Предпо-

ложим, что начальные значения массы непористых сферических частиц различны, растворение частиц

не сопровождается тепловым эффектом, а кинетика растворения отдельной частицы описывается урав-

нением вида

)(),(

нр

mcckcmf

yуy

−χ−==

; (4.61)

)0( mm

где m – масса частицы;

−

эмпирический коэффициент растворения,

[]

3/1

1р

/ µρ∆= Dak

;

−

a эмпириче-

ская константа;

−ρ∆ разность плотностей твердого материала и растворителя; −D коэффициент диффу-

зии;

−µ коэффициент динамической вязкости;

уу

cc ,

– концентрация насыщения и фактическая концен-

трация основной массы раствора;

χ – коэффициент формы частицы (для шарообразной частицы

/36 ρπ=χ

Исходные данные: плотность распределения Р(m

) массы

m частиц в начальный момент времени,

общая начальная масса М

частиц, загруженных в аппарат, объем V

растворителя в аппарате, концен-

трация с

раствора в начальный момент времени, константа k

растворения и концентрация с

ун

насыще-

ния.

Требуется построить математическую модель, позволяющую по исходным данным рассчитывать

зависимости концентраций с

(t) раствора и общей массы М(t) нерастворившихся частиц от времени.

Запишем уравнение кинетики состояния среды, которое при сделанных выше допущениях сводится к

уравнению материального баланса

[]

;)(

)()(

]),,([)(

11нр

3/1

000нр

)(

000

dmdttcckmmPcck

dmctmmfmР





















−χ−−χ=

=−=

∫∫

∫

∞

∧

)0(

cc = ,

где −

∧

)(

mP ненормированная плотность распределения массы

m частиц в начальный момент времени,

−=

∧

00000

),()( NmPNmP число частиц, поступивших в аппарат, .)(/

000

)(

000

dmmPmMN

∫

При решении этого уравнения необходимо учитывать, что масса m частицы может быть отрица-

тельной, что эквивалентно условию

[]

.)(

1нр

3/1

dttсckm

∫

−χ≥

Поскольку масса вещества в растворе увеличивается только за счет уменьшения массы частиц при

их растворении, то общая масса частиц, находящихся в аппарате в момент времени

, рассчитывается

по формуле

)]0()([)(

0 yyy

ctcVMtM −

−

. (4.63)

Приведенная модель (4.61) – (4.63) периодического процесса растворения относится к классу дина-

мических нелинейных моделей с сосредоточенными координатами. Для определения зависимости с

(t)

необходимо вначале одним из численных способов, например, методом Рунге-Кутта четвертого поряд-

ка, решить нелинейное дифференциальное уравнение (4.62). При этом на каждом шаге интегрирования

системы также численным способом, например, методом Симпсона, вычисляются значения определен-

ных интегралов. После этого по соотношению (4.63) можно рассчитать М(t).

4. Модель непрерывного процесса растворения монодисперсных частиц [3]. Предположим, что на

вход аппарата подаются частицы одинаковой массы m

, их растворение не сопровождается тепловым эф-

фектом, а кинетика растворения частиц описывается уравнением (4.61).

Исходные данные:

вх

,,,

cmGG – соответственно расходы твердой фазы и растворителя, масса от-

дельной частицы, концентрация раствора на входе в аппарат; k

– константа растворения; с

ун

– концен-

трация насыщения и V

– объем растворителя, находящегося в аппарате.

Требуется построить математическую модель, позволяющую по исходным данным рассчитывать

концентрацию с

раствора, плотность распределения массы

)(mP

и общую массу

вых

частиц, выгру-

жаемых из аппарата в единицу времени.

Запишем уравнение материального баланса, описывающее состояние среды:

∫

α=−

∧

вх

)]([)(

yyy

dmmPccG

, (4.64)

где

)(α

∧

– ненормированная плотность распределения возраста

частиц в аппарате. Для режима иде-

ального смешения имеем

)/(exp)(

Θα−=α

∧

nP , (4.65)

где

GV /=Θ

– среднее время пребывания частиц в аппарате,

вх

/ mGn = – число частиц, поступающих в

аппарат в единицу времени.

Массовый расход частиц, покидающих аппарат, можно определить из соотношения

)(

вхвхвых

yyy›

ccGGG −+= . (4.66)

(4.62)

Плотность распределения массы частиц на выходе из аппарата удовлетворяет при

0 mm

соот-

ношению

[]













−χΘ

−

−×−χΘ=

−

)(

exp)(

),(

)(

нр

3/13/1

3/2

ннр

cck

mсck

cmf

Приведенная модель (4.61), (4.64) – (4.66) относится к классу статических нелинейных моделей с

сосредоточенными координатами.

5. Модель химического процесса конверсии оксида углерода. В каталитическом трубчатом реакто-

ре (рис. 49) осуществляется экзотермическая обратимая химическая реакция

↑++⇔+ )(HCOOHCO

222

где −)(Th тепловой эффект реакции.

Скорость химической реакции W описывается выражением вида

222

COOH

COH

рOHCO

)(

ccTA

ccTkcc

TkW

−

где

−

ги.COHOHCO

,,,,

222

ccccc

концентрации оксида углерода, воды, водорода, двуокиси углерода и инерт-

ных газов, соответственно; −

−

)(),(),(

TkTATk кинетические параметры, зависящие от температуры T :

























−⋅⋅+⋅⋅+=

−−−

62,2101,01062,0

2240

3,2exp)(

2631

Tk ;

Рис. 49. Структурная схема химического реактора и

элемента каталитического трубчатого реактора

для железохромового катализатора имеем:

;32/3)57,4/(8800lg

,2,10)57,4/(00034lg

+−=

−

для цинкохроммедного катализатора:

.48,3)57,4/(8800lg

,98,12)57,4/(00034lg

+−=

−

Температурные зависимости теплового эффекта реакции )(Th и удельной теплоемкости

)(Tc

описыва-

ются следующими уравнениями:

()

∑

−−

+++=

⋅⋅+⋅⋅−+=

iiiip

TeTdTbaTc

TTTTh

3623

.)(

;10967,010845,2219,000010)(

() () ()

000

,, tGc

tGc ,,

∇

tс ,

dttdсс

coco

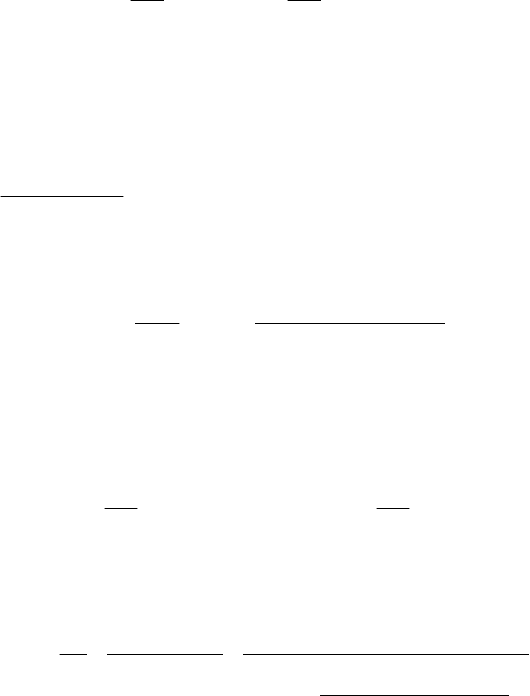
Исходные данные: концентрации

(0)

ги.

(0)

,,,,

222

ccccc оксида углерода, воды, водорода, двуокиси

углерода и инертных газов на входе в реактор; плотность

и концентрация (объемные доли)

c i-го ком-

понента; массовый расход G потока веществ; температура

)0(

потока на входе в реактор; тепловой эффект

реакции h , удельная теплоемкость

c потока веществ в реакторе, кинетические параметры )(),(),(

TkTATk

−

Требуется построить модель химического процесса, осуществляемого в каталитическом реакторе

конверсии оксида углерода (рис. 49), позволяющую рассчитывать температуру и концентрации веществ

в каждой точке и на выходе реактора.

Примем следующие допущения: 1) химический процесс осуществляется в адиабатическом трубча-

том каталитическом реакторе; 2) режим движения газовой смеси в слое катализатора соответствует ре-

жиму идеального вытеснения.

Выберем в качестве ключевого компонента оксид углерода CO и составим по этому компоненту

уравнение материального баланса:

0),()(

рCO

cг.

COCO

сг.

=−

+−

dVTcW

dcс

где

−ρ=ρ

∑

сг.

плотность парогазовой смеси;

−

плотность i-го компонента; −

с концентрация (объ-

емные доли) i-го компонента;

−ρ

сг.

объемный расход потока;

−

объем реактора.

Учитывая, что −

⋅ρ

=τ

3600)/(

сг.

d условное время контакта в слое объемом

и выполнив предель-

ный переход, получим

.)0(

)(

(0)

COOH

COH

pOHCO

222

ccTA

cckcc













−

Далее составим уравнение теплового баланса

0)()(),(

сг.

−+

dTT

cdThTcWT

VVV

и, осуществляя предельный переход, получим

.)0(

)(

),(

)(

)0(

COOH

COH

pOHCO

222

ccTA

cckcc

Tkc

TcWc













+⋅

−

Концентрации водяного пара, водорода, двуокиси углерода и инертных газов рассчитываются из

уравнений материального баланса концентраций веществ по известной концентрации ключевого ком-

понента:

;)(

(0)

)0(

(0)(0)

∆−=

∆−=−−=

cccccc

).(1

;

222

COHOHCOги.

(0)

ccccc

ccc

+++−=

∆−=

Таким образом, математическая модель химического процесса конверсии оксида углерода пред-

ставляет собой статическую модель с распределенными по длине реактора концентрациями веществ

и температурой T и выражается системой нелинейных дифференциальных уравнений в обыкновенных

производных с начальными условиями, решение которой можно получить, например, методом Рунге-

Кутта четвертого порядка точности.

6. Математическая модель непрерывного процесса диазотирования ароматических аминов в

производстве азопигментов. Перечень наиболее вероятных реакций, протекающих при диазотирова-

нии ароматических аминов нитритом натрия, и уравнения кинетики процесса диазотирования приведе-

ны ниже.

Диазотирование (реакция экзотермическая)

растворение твердой фазы амина в среде соляной кислоты

[ArNH

]

→

ArNH

;

образование диазотирующего агента (HNO

)

NaNO

+ HCl →

∞=W

HNO

+ NaCl ;

целевая реакция диазотирования

ArNH

+ HNO

+ HCl →

ArN

Cl + 2H

O + h (T) ↑ ;

разложение азотистой кислоты

3HNO

→

2NO + HNO

+ H

O ;

образование диазосмол

ArN

Cl + HNO

→

;

разложение диазосоединения с образованием диазосмол

ArN

Cl →

;

образование диазоаминосоединений

ArN

Cl + ArNH

→

H + HCl.

5. Уравнения кинетики и кинетические константы

процесса диазотирования

Кинетиче-

ское уравнение

Порядок ре-

акции

Предэкспо-

ненци-

альный мно-

житель, (м

)

/моль

n-1

/с

Энергия

активации,

Дж/моль⋅1

–3

(T)⋅[ArNH

]⋅[HNO

]

3,75⋅10

46,82

/]HNO[)( PTk ⋅

7,17⋅10

/(9,81⋅1

119,65

)

(T)⋅[ArN

Cl]⋅[HNO

]

0,32⋅10

63,69

= k

(T)⋅[ArN

Cl]

1,10⋅10

87,15

Обозначения: А – ArNH

(амин); АК – HNO

; СК – HCl; σ – NO; D – ArN

Cl (диазосоединение);

),(

χχ=χ ;

P – парциальное давление нитрозных газов; r – радиус частицы амина; l – текущая коорди-

ната длины реактора;

– равновесная концентрация амина;

– плотность и молекулярная масса

амина;

),( lr

∧

– ненормированная плотность распределения числа N частиц амина по размеру, т.е.

drdN /=ψ

∧

;

NSl

GGG ,, – расходы жидкой и твердой фаз суспензии амина и нитрита натрия;

тр

S – площадь

поперечного сечения трубы реактора;

– теплоемкость; ϑ – скорость потока; K – коэффициент тепло-

передачи; h – тепловой эффект реакции; индексы: (0) – вход в реактор; х – хладагент; (i) – точка распре-

деленного по длине ввода реагентов в реактор.

На рис. 50 представлены трубчатые турбулентные аппараты, позволяющие осуществлять процессы

тонкого органического синтеза с твердой фазой в высокотурбулентных потоках.

Схема материальных потоков в трубчатом реакторе приведена на рис. 51.

При составлении уравнений математической модели примем следующие допущения: 1) реакция

диазотирования протекает в растворе и диазоаминосоединение в процессе диазотирования не образует-

ся, т.е. ;0

=W 2) гидродинамические режимы течения реакционной смеси и хладагента близки к режиму

идеального вытеснения; 3) реактор является объектом с распределенными только по длине l координа-

тами, скорость потока ;const)(

ϑ l 4) потери тепла в окружающую среду пренебрежимо малы;

5) теплофизические характеристики принимаются постоянными в рабочем диапазоне температур; 6)

форма кристаллов амина близка к сферической.

III

а)

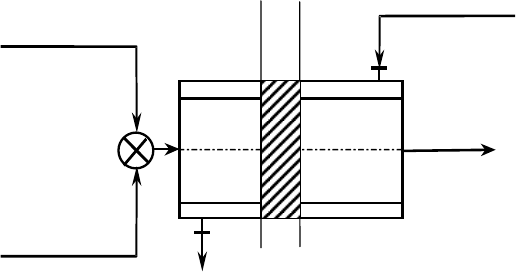
Рис. 50. Малогабаритные турбулентные трубчатые реакторы:

а – цилиндрического типа; б – диффузор-конфузорного типа;

в – комбинированного типа;

– диаметр диффузора, d – диаметр конфузора; I, II, III, IV – потоки веществ

Рис. 51. Схема материальных потоков

в трубчатом реакторе диазотирования:

ψ (r) – гранулометрический состав; х – хладагент; l – жидкая фаза;

S – твердая фаза; σ, χ – нитрозные газы и диазосмолы, соответственно

,TG

раствор

диазосоединения

(

)

(

)

(

)

000

NNN

TGc

(

)

(

)

() ()

LcLc

LGLG

AKD

водный раствор

нитрита натрия

() () ()

000

T,Gc

() () ()

000

CKA

Gcc

()

,,0, TrG

cолянокислая

суспензия

амина

хладагент

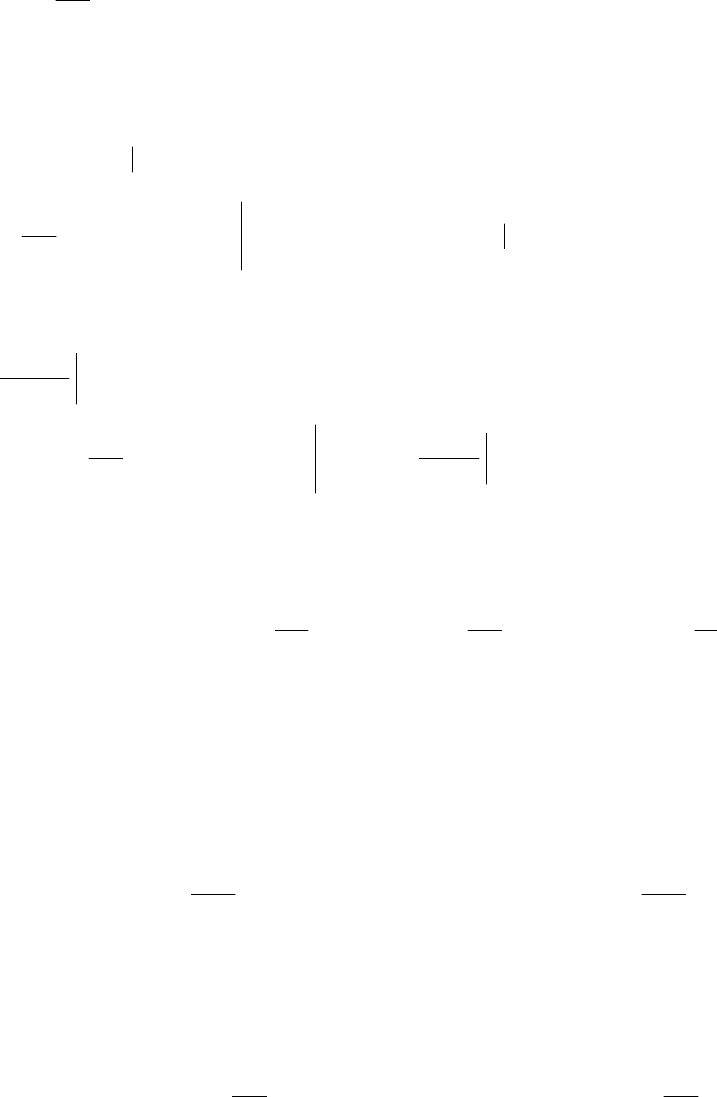
С учетом принятых обозначений и допущений составим уравнения материального покомпонентно-

го баланса на участке трубы (

, ll

) за промежуток времени (

, tt ) например, по растворенному амину:

[]

∫∫

∫∫∫

ξξ−ξ=ξ







ξψ−







−+−

∞

∧

.),(),(),(),(

),,()()(

121

212

AKAAAl

dtCtCSdtddrTcWr

TccWSdtlclcG

Пользуясь теоремой о среднем, получим равенство

[]

,),(),(),(),(

),,()()(

212

ltctcStldrTcWr

TccWStlclcG

AKA

AAt

∆ξ−ξ=∆∆







ξψ−







−+∆−

=ξ

∞

∧

∫

которое при помощи теоремы о конечных приращениях можно преобразовать к виду

),(

),(),(

),,(

),(

tlc

StldrTcWr

TccWSlt

tlc

AKA

∆∆

∂

=∆∆







ξψ−







−+∆∆

∂

=ξ

∞

∧

∫

Переходя к пределу при lll →

, и ttt →

, , получим уравнение

;),(),(

),,(

drTcWrl

TccW

AKA

∂

=ψ−+

∂

∫

∞

∧

(4.67)

).(),0();()0,(

)0(

tctclclc

Аналогичным образом можно получить уравнения динамики трубчатого реактора и для других

компонентов реакционной смеси:

• по азотистой кислоте (АК):

;),,(),(),,(

432

TccWTcWTccW

DAKAKAKA

∂

=+++

∂

(4.68)

);(/)(),0();()0,(

)0()0(

)0(

tGtGctclclc

NAK

• по диазосоединению (D):

;),(),,(),,(

542

TcWTccWTccW

DDAKAKA

∂

=++−

∂

(4.69)

);(),0();()0,(

)0(

tctclclc

• по продуктам разложения

:),( χσ