Дворецкий С.И., Ермаков А.А., Пешкова Е.В. Расчет и оптимизация процессов и аппаратов химических и пищевых производств в среде MatLab

Подождите немного. Документ загружается.

Корни произвольного уравнения по заданному приближению позволяет найти встроенная функ-

ция fzero, которая вызывается следующим образом:

>> x = fzero(‘myfunction’, x0)

где ‘myfunction’ – имя файл-функции, вычисляющей левую часть уравнения; x0 – начальное приближе-

ние к корню либо вектор, содержащий концы отрезка, на котором ищутся корни; x – найденное при-

ближенное значение корня. Данная функция находит решение с точностью до шестнадцатого знака по-

сле запятой.

П р и м е р: Известна концентрация недиссоциированной кислоты

[

]

HA – 0,1 моль

–1

; константа дис-

социации

K – 1,85 · 10

–5

; ионное произведение воды

K – 1 · 10

–14

. Требуется определить кислотность рас-

твора.

Зависимость pH от перечисленных функций представлена следующим уравнением:

[]

[

]

[]

−+

−

, где

[

]

H – концентрация ионов водорода. Значение pH – это отрицательный

десятичный логарифм концентрации ионов водорода: )log(pH

−= H .

Функция, содержащая выражение для расчета pH, сохранена под именем concentr, а входным аргу-

ментом ее является значение концентрации ионов водорода.

function f = concentr(x)

% определение pH растворов слабых кислот

kw = 1.85e-5;

ka = 1.0e-14;

ha = 0.1;

f = (x^2-kw)/ka+x-(kw/x)-ha;

В программе aim производится построение графика функции concentr для определения начального

приближения, а затем решение нелинейного уравнения и определение pH.

% программа aim определения pH раствора

% построение графика функции для определения

% начального приближения

fplot ('concentr', [0 0.02])

grid on

% вызов fzero от файл-функции concentr, и точки приближения

% с определением значения функции в точке полученного решения

[H, f] = fzero('concentr', 0.004)

% расчет pH

pH = -log10(H)

Результаты поиска начального приближения приведены на рис. 6.2.

Результаты реализации программы aim:

>> aim

H =

0.0043

f =

-3.0669e-007

pH =

2.3664

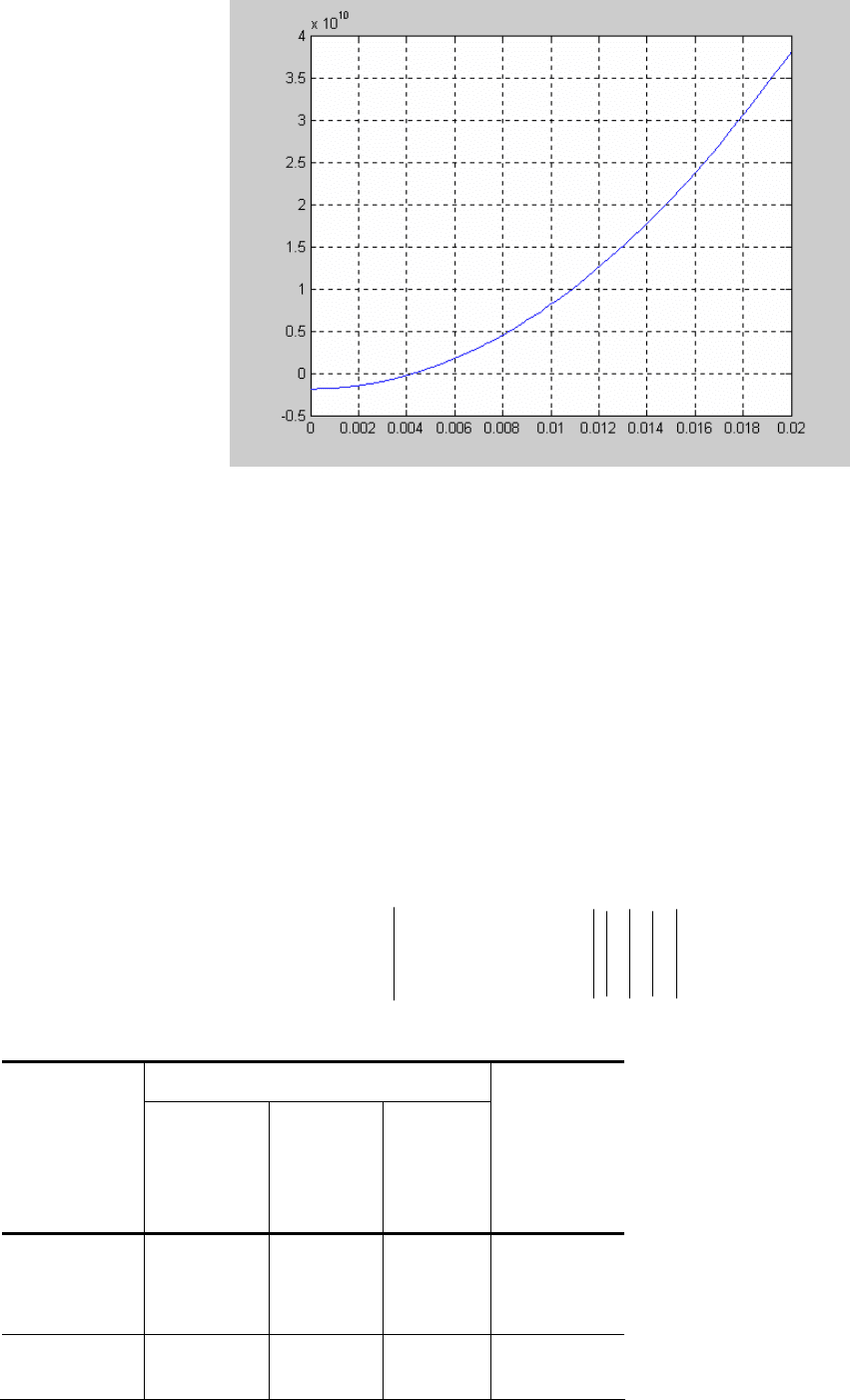
По графику легко определяется значение аргумента, близкого к нулю, которое является начальным

приближением. Значение функции от полученного решения достаточно близко к нулю.

Решение систем линейных уравнений осуществляется при помощи символа «\», при этом систе-

ма линейных уравнений представляется в матричном виде.

Рис. 6.2 Определение начального приближение

для поиска корней уравнения

П р и м е р: Требуется согласовать производство трех групп химических заводов, как по линии вза-

имных связей, так и по линии выполнения заданной им программы на производство конечной продук-

ции. Исходные данные: программа на конечную продукцию каждой группы заводов и прогрессивные

величины норм расходов этих продуктов как сырья для взаимного и собственного воспроизводства –

представлены в табл. 8.

Математически согласованное производство по данным выпусков данных групп заводов с учетом

прогрессивных норм расхода записывается в виде прогрессивных норм расхода или в матричной форме:

()











=−−−

;

333,322,311,33

233,222,211,22

133,122,111,1

yxaxaxax

yxaxaxa

3,32,33,1

3,22,21,2

3,12,11,1

aaa

=⋅

−−−

8 Исходные данные

Норма расхода, т/т

Нефте-

химиче-

ские про-

дукты

Химиче-

ские

продук-

ты

Изделия

из пла-

стмассы

Програм-

ма на про-

дукцию

Нефтехи-

мические

заводы, x

0,08 0,04 0,01 50 000

Заводы хи-

мической

0,07 0,06 0,02 30 000

промыш-

ленности,

Заводы пе-

реработки

пластмасс,

0,09 0,08 0,01 80 000

После подстановки исходных данных система имеет вид

00080

00030

00050

99,008,009,0

02,094,007,0

01,004,092,0

=⋅

−−

Решим данную задачу двумя возможными способами – с использованием матричных операций и

оператора «\», и произведем проверку полученного решения. Расчет материального баланса приведен в

листинге программы linesist.

% задание матрицы коэффициентов и столбца свободных членов линейной системы

A = [0.92 -0.04 -0.01; -0.07 0.94 -0.02; -0.09 -0.08 0.99];

B = [50000; 30000; 80000];

% решение системы с использованием матричных операций

X1 = A^-1*B

% решение системы с использованием оператора \

X2 = A\B

% проверка правильности результатов решений

REZ1 = A*X1 % решение, полученное с помощью матричных операций

REZ2 = A*X2 % решение, полученное с помощью оператора \

Результаты реализации программы linesist:

>> linesist

X1 =

1.0e+004 *

5.6970

3.8052

8.9062

X2 =

1.0e+004 *

5.6970

3.8052

8.9062

REZ1 =

1.0e+004 *

5.0000

3.0000

8.0000

REZ2 =

1.0e+004 *

5.0000

3.0000

8.0000

6.3 Вычисление корней полинома и производных от полинома

Полином задается вектором его коэффициентов, число элементов вектора, т.е. число коэффициен-

тов полинома всегда на единицу больше его степени, нулевые коэффициенты должны содержаться в

векторе.

Вычисление значения полинома от некоторого аргумента:

>> p = [1 0 3.2 -5.2 0 0.5 1 -3];

>> polyval(p, 3)

ans =

2.5479e+003

Нахождение сразу всех корней полинома осуществляется при помощи функции roots, которая воз-

вращает вектор корней полинома, в том числе и комплексные.

>> r = roots(p)

r =

-0.5668 + 2.0698i

-0.5668 – 2.0698i

-0.6305 + 0.5534i

-0.6305 – 0.5534i

1.2149

0.5898 + 0.6435i

0.5898 – 0.6435i

Встроенная функция polyder предназначена для вычисления производных от полиномов. Вызов

polyder с аргументом – вектором, соответствующим полиному, приводит к вычислению вектора коэф-

фициентов производной полинома:

>> p = [1 0 1 0 0 1];

>> p1 = polyder(p)

p1 =

5 0 3 0 0

6.4 Интегрирование функций

Для вычисления интеграла используется quad, задавая первым аргументом имя файл-функции, от

которой вычисляется интеграл, а вторым и третьим – нижний и верхний предел интегрирования. Данная

функция вычисляет приближенное значение интеграла с точностью 10е-3.

>> I = quad('myfunction', a, b)

П р и м е р: Вычислить летучесть аммиака f как функцию давления при заданной температуре.

Наиболее точные значения коэффициента летучести получают из экспериментальных значений коэф-

фициента сжимаемости, определяемого из P-V-T измерений. Зависимость сжимаемости аммиака от дав-

ления определена экспериментально (табл. 9).

Для вычисления летучести как функции давления при заданной температуре используется зависи-

мость:

∫

−

где Z – функция сжимаемости газа; P – давление; f – летучесть аммиака.

Вычислить летучесть и объем газа при заданных условиях.

9 Зависимость сжимаемости аммиака от давления

№

опыта

Давле-

ние

Функция

сжимае-

мости газа

№ опы-

та

Давле-

ние

Функция

сжимае-

мости газа

1 1 0,998 9 100 0,801

2 10 0,981 10 200 0,551

3 20 0,961 11 300 0,462

4 30 0,942 12 400 0,495

5 40 0,922 13 500 0,557

6 50 0,902 14 600 0,621

7 60 0,882 15 800 0,755

8 80 0,841

В функции ammiak1 записывается подынтегральная функция

function f = ammiak1(p, z)

% расчет зависимости летучести аммиака

% z – независимый параметр (летучесть)

f = (z-1)./p;

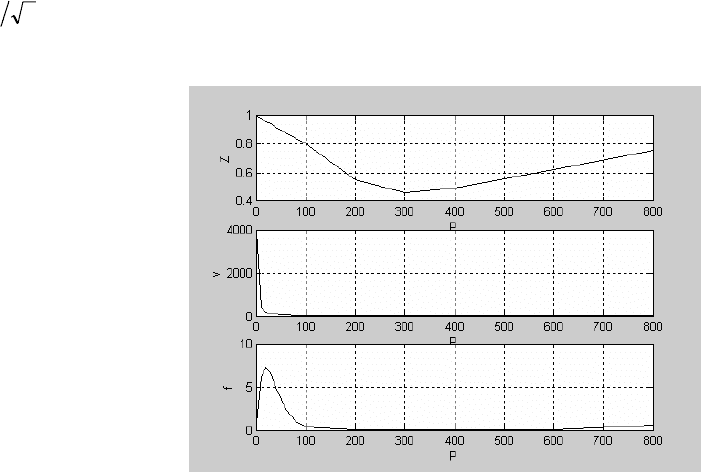
Процедура ammiak рассчитывает летучесть и объем газа, результаты расчета выводятся на графики

в одно окно.

% программа ammiak расчета летучести аммиака

% в зависимости от давления

% с использованием оператора for

R = 8.31514; % универсальная газовая постоянная

T = 473; % температура, К

% табличные данные

P = [0.001 1 10 20 30 40 50 60 80 100 200 300 ...

400 500 600 800];

Z = [0 0.998 0.981 0.961 0.942 0.922 0.902 0.882...

0.841 0.801 0.551 0.462 0.495 0.557 0.621 0.755];

% Расчет

for i=1:length(P)

I = quad('ammiak1', 1.0e-10, P(i), [], [], Z(i));

f(i) = P(i)*exp(I); % летучесть аммиака

v(i) = (Z(i)*R*T)/P(i); % объем газа

end

% графический вывод результатов

subplot(3,1,1)

plot ( P, Z, 'k-')

xlabel('P')

ylabel('Z')

grid on

subplot(3,1,2)

plot ( P, v, 'k-')

xlabel('P')

ylabel('v')

grid on

subplot(3,1,3)

plot ( P, f, 'k-')

xlabel('P')

ylabel('f')

grid on

Результаты расчета на отдельных графиках представлены на рис. 6.3.

Реализованный алгоритм основан на квадратурной формуле Симпсона с автоматическим подбором

шага интегрирования для достижения требуемой относительной погрешности. Интегрирование гладких

функций лучше производить при помощи quad8, основанной на наиболее точных квадратурных форму-

лах Ньютона-Котеса с автоматическим подбором шага.

При вычислении в MatLab 5.2, 5.3 интегралов от функций, имеющих интегрируемую особенность,

например x1 , в нуле выводится сообщение об ошибке. В версии 6.0 данный алгоритм улучшен для

функций с особенностями, и, кроме того, появился quadl для нахождения определенного интеграла по

квадратурным формулам Гаусса-Лобатто.

Рис. 6.3 Результаты реализации программы ammiak

Также в MatLab имеются функции для вычисления двойных интегралов: dblquad. Используется

следующим образом:

>> dblquad(‘myfunction’, a, b, c, d)

где a, b – нижний и верхний пределы внутреннего интеграла; c, d – нижний и верхний пределы наруж-

ного интеграла.

Также имеется возможность вычислять интегралы с переменным верхним пределом. Вычисление

такого интеграла производится теми же функциями, что обычные определенные интегралы. Для нахож-

дения такого интеграла пишутся две функции: для подынтегральной функции и находящую значения

интеграла для каждого значения переменного верхнего предела (это число является входной перемен-

ной данной функции).

6.5 Интерполирование

Табличные данные очень часто удобно интерпретировать как некоторую функцию, в частности

сплайн (полиномиальную) (рис. 6.4). Если возникает задача о построении полиномиальной или кусоч-

но-полиномиальной функции для приближения некоторых исходных данных, то существуют в MatLab

встроенные функции для приближения сплайнами как одномерных, так и многомерных данных. Неко-

торые встроенные функции интерполирования в MatLab приведены в табл. 10.

10 Функции MatLab для интерполяции табличных данных

Функция Назначение Примечания

P = polyfit(x, y,

Приближение

функции одной

переменной по

методу наимень-

ших квадратов

x, y – вектора, со-

держащие таб-

лично заданную

функцию; a – чис-

ло, равное степе-

ни приближаю-

щего полинома

P = interp1(x, y,

xi, ‘text’)

где text =

Приближение

функции одной

переменной

сплайнами.

nearest Интерполяция по

соседним элемен-

там.

linear Линейная интер-

поляция.

Spline Интерполяция

кубическими

сплайнами

x, y – вектора, со-

держащие таб-

лично заданную

функцию; xi –

вектор, содержа-

щий про-

межуточные рав-

ноотстоящие точ-

ки; text – способ

приближения

функции

Продолжение табл. 10

Функция Назначение Примечания

P = interp2(X, Y,

Z, Xi, Yi, ‘text’)

где text =

Приближение

функции двух пе-

ременной сплай-

нами.

nearest Интерполяция по

соседним элемен-

там.

bilinear Билинейная ин-

терполяция.

bicubic Интерполяция

бикубическими

сплайнами

X, Y, Z – вектора,

содержащие таб-

лично заданную

функцию; Xi, Yi –

вектора, содер-

жащие промежу-

точные равноот-

стоящие точки;

text – способ при-

ближения функ-

ции

Более подробно об интерполировании таблично заданных функций можно узнать из справочной

системе MatLab.

П р и м е р: Интерполяция таблично заданных функций.

% задание табличной функции

x = [0.1 0.2 0.4 0.5 0.6 0.8 1.2];

y = [-3.5 -4.8 -2.1 0.2 0.9 2.3 3.7];

% задание промежуточных точек для интерполирования

xi = [x(1):0.01:x(length(x))];

ynear = interp1(x, y, xi, 'nearest');

yline = interp1(x, y, xi, 'linear');

yspline = interp1(x, y, xi, 'spline');

Рис. 6.4 Различные способы интерполяции функции одной переменной

6.6 Оптимизация

В состав MatLab входят функции, предназначенные для решения линейных и нелинейных, безус-

ловных и условных оптимизационных задач. Основные функции оптимизации приведены в табл. 11.

11 Основные функции MatLab для решения задач оптимизации

Функция Применение

Примеча-

ние

Безусловная оптимизация

fmin(‘F’,x1,x

2,…

op-

tions,P1,P2)

Поиск локального минимума

функции одной переменной.

'F' – имя файл-функции; x1,x2

– левая и правая границы ин-

тервала, на котором ищется

минимум; options – параметры

управления процессом реше-

ния; P1,P2 – независимые па-

раметры

В поздних

версиях

перенесен

в fminbnd

fminbnd(‘F’,

x1,x2,…

op-

tions,P1,P2)

Поиск локального минимума

функции одной переменной на

заданном интервале. Приме-

нение аналогично fmin

Для вер-

сий 6.x

fmins(‘F’,X0,

…

op-

tions,P1,P2)

Поиск локального минимума

функции нескольких перемен-

ных. 'F' – имя файл-функции;

X0 – вектор начальных при-

ближений; options – параметры

управления процессом реше-

ния; P1,P2 – независимые па-

раметры

В поздних

версиях

перенесен

в fmin-

fmin-

search(‘F’,X0

,…

op-

tions,P1,P2)

Поиск локального минимума

функции нескольких перемен-

ных. Применение аналогично

fmins

Использу-

ет сим-

плексные

методы.

Для вер-

сий 6.x

fmin- Поиск минимума нелинейной Использу-

unc(‘F’,X0,

…

op-

tions,P1,P2)

функции нескольких перемен-

ных без ограничения на пере-

менные. Применение анало-

гично fmins

ет ква-

зиньюто-

новские

методы.

Для вер-

сий 6.x

Условная оптимизация

lin-

prog(f,A,b,…

Aeq,Beq,LB,

…

UB,X0,optio

ns)

Решение задач линейного про-

граммирования. f – вектор ко-

эффициентов; A,b,Aeq,Beq –

вектора коэффициентов нели-

нейных и линейных ограниче-

ний; LB,UB – вектора верхних

и нижних границ изменения

переменных; X0 – вектор на-

чальных приближений; options

– параметры управления про-

цессом решения

Для вер-

сий 6.x

Продолжение табл. 11

Функция Применение

Примеча-

ние

quad-

prog(H,f,A,b,

…

Aeq,Beq,LB,

UB,…

X0,options)

Решение задач квадратичного

программирования. H– вектор

соответствующих коэффици-

ентов, остальные параметры –

аналогично linprog

Для версий

6.x

fmin-

con(‘fun’,X0,

A,B,…

Aeq,Beq,LB,

UB,…

’nonl-

con’,options,

…

P1,P2)

Решение задач нелинейного

программирования. ‘fun’ – имя

файл-функции, содержащей

целевую функцию, ’nonlcon’ –

имя файл-функции, содержа-

щей нелинейные ограничения,

остальные параметры – анало-

гично linprog

Для версий

6.x

fmini-

max(‘fun’,X0

,…

A,B,Aeq,Beq

,LB,UB,…

’nonl-

con’,options,

…

P1,P2)

Решение минимаксной задачи.

Применение аналогично fmin-

con

Для версий

6.x

fgoalat-

tain(‘fun’,X0,

…

g,w,A,B,Aeq,

Beq,…

LB,UB,’nonl

con’,…

op-

Решение задачи о достижении

границы. Решается задача ви-

да

gwxF ≤−

)( . Остальные па-

раметры аналогичны fmincon.

Для вер-

сий 6.x

tions,P1,P2)

1 Безусловная минимизация функций. Минимизация функции одной переменной производится

с помощью команды fminbnd. Данная команда определяет локальный минимум в точке, близкой к точке

приближения. Использование этой команды аналогично использованию команды fzero.

П р и м е р: Найти локальный минимум уравнения

0)cos(sin

=− xxx

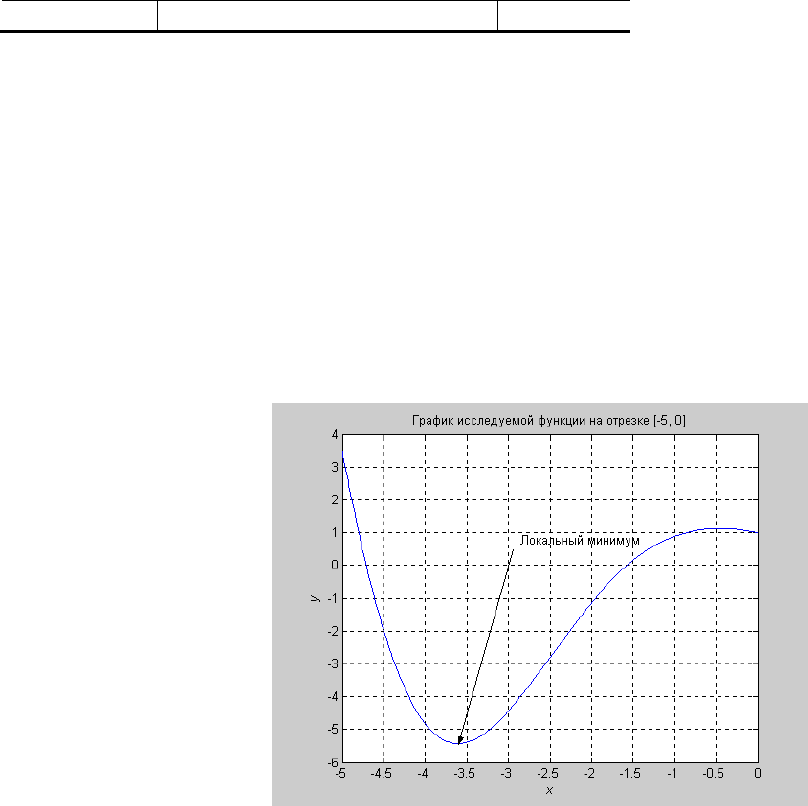
на отрезке [–5, 0]. Исследуемая

функция сохраняется в файл-функции 'myf', график исследуемой функции представлен на рис. 6.5.

>> x = fminbnd('myf', -5, 0)

x =

-3.6052

Рис. 6.5 Иллюстрация к примеру

Если необходимо найти безусловный минимум функции нескольких переменных, то используется

команда fminsearch. перед применением fminsearch необходимо создать файл-функцию, вычисляющую

значения искомой функции, причем аргументом данной функции должен быть вектор, элементы кото-

рого являются аргументами минимизируемой функции.

П р и м е р. Определить локальный минимум функции

yxyxf

sinsin),( .

Сначала исследуем поведение данной функции для определения хорошего начального приближе-

ния. Для этого построим линии равного уровня исследуемой функции (рис. 6.6).

Файл-функция для оптимизации:

function f = ftest(arg)

x = arg(1);

y = arg(2);

f = sin(pi*x).*sin(pi*y);

Зная начальное приближение (определяется из графика на рис. 6.6), можно вызвать функцию fmin-

search (указывая вектор начального приближения).

>> M = fminsearch('ftest', [1.4, 0.6])

M =

1.5000 0.5000