Дудаков С.М. Математическое введение в информатику
Подождите немного. Документ загружается.


6.3.
∗
Аппликативное и функциональное программирование 161
Sub S;
arg x, y;
S = S
1
(x, y, 0) ;
end;
Sub S
1
;
arg x, y, z;
if y < x then
S
1
= S
1
(x, succ (y) , succ (z)) ;
else
S
1
= z;
end;
end;
Рис. 6.5: Вычитание чисел.
6.3
∗
Аппликативное и функциональное программи-
рование
В этом параграфе мы докажем, что вызовы подпрограмм могут заменить
и оператор присваивания, и оператор цикла. Но прежде чем делать это
в общем случае рассмотрим пример.
Пример 6.17. Изменим подпрограмму, вычисляющую разность, и вве-
дем вспомогательную подпрограмму, см. рис. 6.5.
Как видим, ни одна из подпрограмм не содержит ни операторов
цикла, ни операторов присваивания, за исключением специального слу-
чая, который используется для изменения выходной переменной ре-
зультата вычисления подпрограммы. Докажем, что подпрограмма S
действительно вычисляет разность чисел.
Утверждение 6.1. для любого состояния σ выполнено
Π
S
1
(σ) (S
1
) = bσx − σyc + σz.
Доказательство. Докажем это индукцией по bσx − σyc.
Базис индукции.
bσx − σyc = 0. То есть σy ≥ σx. Тогда
Π
S
1
(σ) = (S
1
= z; ) (σ) = τ,
где τ отличается от σ только тем, что
τ (S
1
) = σz = bσx − σyc + σz.
Следовательно,
Π
S
1
(σ) (S
1
) = bσx − σyc + σz.

162 Глава 6. Подпрогра ммы, функциональное программирование
Шаг индукции.
Пусть для bσx −σyc < n утверждение доказано, n > 0 и bσx −σyc = n.
Тогда σx > σy, следовательно,
Π
S
1
(σ) = (S
1
= S
1
(x, succ (y) , succ (z)) ; ) (σ) .
Чтобы определить значение выражения S
1
(x, succ (y) , succ (z)) на состо-
янии σ, рассмотрим τ такое, что
τx = σx, τy = σ (succ (y)) = σy + 1,
τz = σ (succ (z)) = σz + 1.
Определим Π
S
1
(τ). Заметим, что
bτx − τyc = bσx − σy − 1c < bσx − σyc = n.
По индукционному предположению:
Π
S
1
(τ) (S
1
) = bτx − τ yc + τz =
= bσx − σy − 1c + σz + 1 = bσx − σyc + σz.
Следовательно, Π
S
1
(σ) (S
1
) = Π
S
1
(τ) (S
1
) = bσx − σyc + σz.
Следствие 6.3. Если σz = 0, то Π
S
1
(σ) (S
1
) = bσx − σyc.
Следствие 6.4. Π
S
(σ) (S) = bσx − σyc .
Итак, мы доказали, что рассмотренный пример корректен.
Теперь рассмотрим, как избавиться от присваиваний и циклов в об-
щем случае.
Определение 6.16. (Аппликативная программа) Программа
называется аппликативной, если она не содержит операторов при-
сваивания (кроме присваиваний выходной переменной).
Определение 6.17. (Функциональная программа)
Аппликативная программа называется функциональной, если она
не содержит циклов.
Соответственно, алгоритм мы будем называть аппликативным (функ-
циональным), если он состоит исключительно из аппликативных (функ-
циональных) программ.

6.3.
∗
Аппликативное и функциональное программирование 163
Обычный оператор присваивания часто называют также оператором
разрушающего присваивания, поскольку он уничтожает значение пере-
менной, которое было до его выполнения. Аппликативная программа
(apply — применять) называется так, потому что разрушения не про-
исходит, и все полученные результаты хранятся до конца.
Функциональная программа так называется, потому что единствен-
ный разрешенный оператор — ветвление. В конце параграфа мы пока-
жем, что если бы у нас была специальная операция IF (x, y, z), которая
бы вычисляла первый аргумент и в зависимости от того истинен он или
ложен возвращала значение второго или третьего аргумента, то можно
было бы обойтись и без этого оператора, то есть программы содержали
бы только вызовы подпрограмм. Более того, существует теория функци-
онального программирования, где доказывается, что можно обойтись и
без такой операции, если изменить обычные понятия истинности и лож-
ности.
Итак, перейдем к доказательству основных теорем.
Теорема 6.1. (О функциональных программах) Всякий алго-
ритм эквивалентен некоторому функциональному алгоритму.
Доказательство. Прежде всего, несколько замечаний. Будем считать,
что тело каждой подпрограммы является структурированной програм-
мой. Мы знаем, что этого можно добиться (теорема о структуризации).
Далее, основную программу с телом Π мы выделим в отдельную под-
программу, например, A
0
. То есть основную программу
Alg A;
arg x
1
, . . . , x
n
;
Π
end;
заменяем на
Sub A
0
;
arg x
1
, . . . , x
n
;
(Π)
A
A
0
end;
Alg A;
arg x
1
, . . . , x
n
;
A = A
0
(x
1
, . . . , x
n
) ;
end;

164 Глава 6. Подпрогра ммы, функциональное программирование
Ясно, что полученный алгоритм эквивалентен исходному.
Будем считать, что в теле любой подпрограммы f оператор f = e;
встречается один раз и идет последним. Если это не так, то этого можно
добиться, введя новую переменную u, заменив всюду оператор f = e; на
оператор u = e; и добавив в конце тела f оператор f = u;
Мы будем предполагать, что все переменные любой подпрограммы
(кроме, конечно, выходной переменной) являются ее аргументами. Этого
тоже нетрудно добиться, достаточно включить их в список после arg, а
в выражениях с использованием подпрограмм подставить для них нули.
Заметим, что при соблюдении этих условий выполняется такое утвер-
ждение. Если x — аргументы подпрограммы f, то для любого состояния
σ
σ (f (x)) = Π
f
(σ) (f) .
С каждой программой Π свяжем некоторое натуральное число
w (Π) — вес. Это будет мера «испорченности программы» по сравнению
с функциональной. Определим его индуктивно для тела подпрограммы
f:
1. Π ∼ x = e; w (Π) = 1, если x 6∼ f, и w (Π) = 0, если x ∼ f.
2. Π ∼ Π
1
Π
2
. Если Π
1
не является следованием, то w (Π) = w (Π
1
) +
2w (Π
2
) + 1.
3. Π ∼ if T then Π
1
end; w (Π) = 2w (Π
1
) + 1.
4. Π ∼ if T then Π
1
else Π
2
end; w (Π) = 2 (w (Π
1
) + w (Π
2
)).
5. Π ∼ while T do Π
1
end; w (Π) = 2w (Π
1
) + 2
w(Π
1
)+1
+ 2.
Если алгоритм A состоит из подпрограмм f
1
, . . . , f
n
и основной про-
граммы Π
A
, то w (A) = w (Π
A
) + w (Π
f
1
) + ··· + w (Π
f
n
).
Пусть тело некоторой подпрограммы f не удовлетворяет определению
функциональной программы. Возможны четыре варианта:
1. Π
f
∼ x
i
= e; Π
0
2. Π
f
∼ if T then Π
0
end; Π
00
3. Π
f
∼ if T then Π
0
else Π
00
end; Π
000
4. Π
f
∼ while T do Π
0
end; Π
00
f = u;

6.3.
∗
Аппликативное и функциональное программирование 165
В последнем случае мы без ограничения общности предполагаем, что
u является переменной. Выше мы сказали, что этого можно добиться.
Рассмотрим, как разобраться с каждым из этих случаев.
1. Создадим новую подпрограмму f
1
и заменим подпрограмму f всю-
ду подпрограммой
˜
f:
Sub
˜
f;
arg x
1
, . . . , x
n
;
˜
f = f
1
(x
1
, . . . , x
i−1
, e, x
i+1
, . . . , x
n
) ;
end;
Sub f
1
;
arg x
1
, . . . , x
n
;
(Π
0
)
f
f
1
end;
Рассмотрим σ
˜
f (e
1
, . . . , e
n
)
. По определению
σ
˜
f (e
1
, . . . , e
n
)
= Π
˜
f
(τ)
˜
f
,
где τ x
j
= σ (e
j
). Далее,
Π
˜
f
(τ)
˜
f
= τ (f
1
(x
1
, . . . , x
i−1
, e, x
i+1
, . . . , x
n
)) = Π
f
1
(ρ) (f
1
) ,
где ρx
j
= τ x
j
кроме того, что ρx
i
= τ (e) и ρf
1
= 0. Но тогда
Π
f
1
(ρ) (f
1
) = Π
f
1
((x
i
= e; ) (τ)) (f
1
) ,
по определению семантики присваивания и, потому что переменная f
1
встречается в Π
f
1
один раз в конце, а переменная
˜
f не встречается вовсе.
Используем лемму о замене переменной:
Π
˜
f
(τ)
˜
f
= Π
f
1
((x
i
= e; ) (τ)) (f
1
) =
= (Π
0
)
f
f
1
((x
i
= e; ) (τ)) (f
1
) = Π
0
((x
i
= e; ) (τ)) (f) = Π
f
(τ) (f) .
Из этого следует, что
σ
˜
f (e
1
, . . . , e
n
)
= σ (f (e
1
, . . . , e
n
)) .
Рассмотрим, как в ходе такого преобразования изменяется вес:
w (Π
f
) ≥ 2w (Π
0
) + 1,
w (Π
0
) + w
Π
˜
f
= w (Π
0
) < w (Π
f
) .
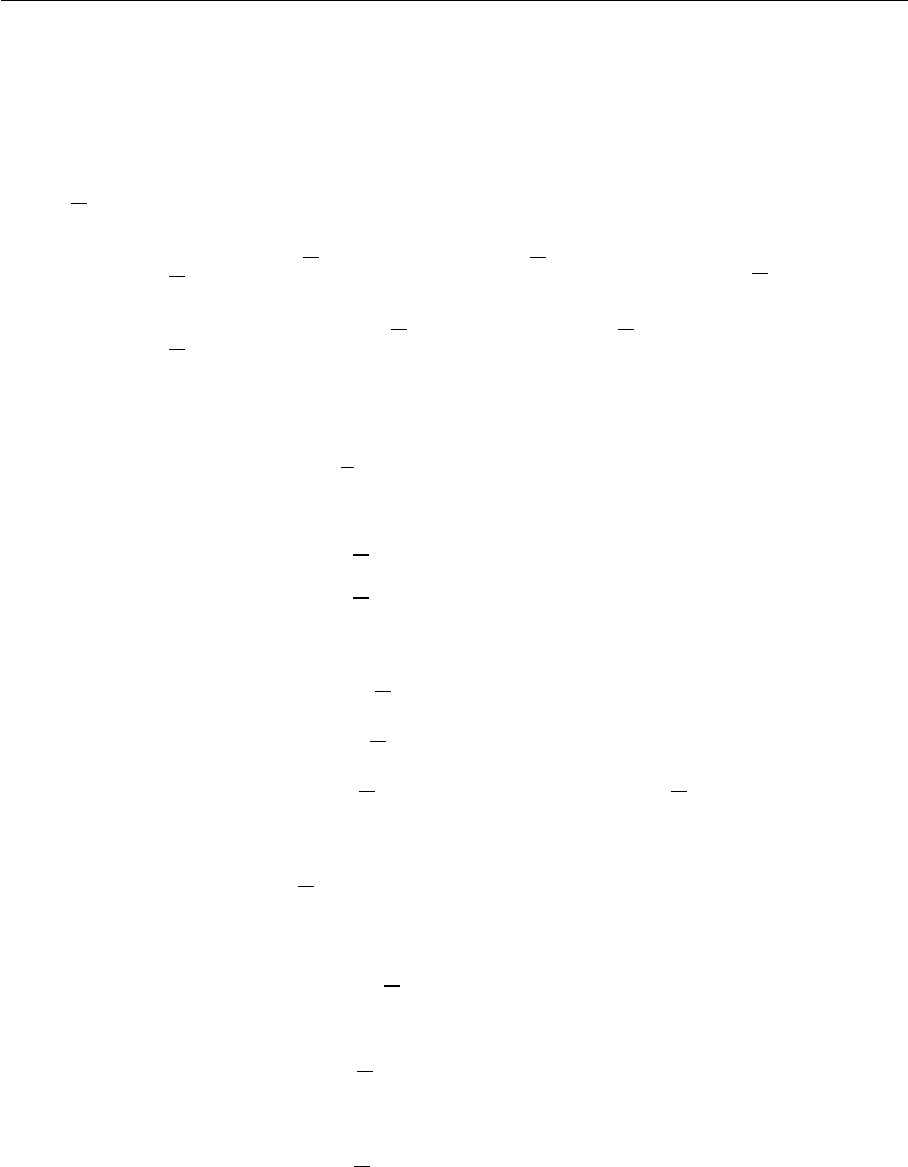
166 Глава 6. Подпрогра ммы, функциональное программирование
2. Аналогично следующему пункту.
3. Построим три новые подпрограммы f
1
, f
2
и f
3
, а f заменим всюду
на
˜
f:
Sub
˜
f;
arg x;
if T then
˜
f = f
1
(x) ;
else
˜
f = f
2
(x) ;
end;
end;
Sub f
1
;
arg x;
Π
0
f
1
= f
3
(x) ;
end;
Sub f
2
;
arg x;
Π
00
f
2
= f
3
(x) ;
end;
Sub f
3
;
arg x;
(Π
000
)
f
f
3
end;
Итак, рассмотрим σ
˜
f (e)
= Π
˜
f
(τ)
˜
f
, где τx
i
= σ (e
i
). По опреде-
лению,
Π
˜
f
(τ)
˜
f
=
τ (f
1
(x)) , если τ |= T ;
τ (f
2
(x)) , если τ 6|= T ;
не определено, если τ (T ) не определено.
Рассмотрим, например, τ (f
1
(x)).
τ (f
1
(x)) = Π
f
1
(τ) (f
1
) =
= (Π
0
f
1
= f
3
(x) ; ) (τ ) (f
1
) = Π
0
(τ) (f
3
(x)) .
Для всякого состояния ρ имеем
ρ (f
3
(x)) = Π
f
3
(ρ) (f
3
) = Π
000
(ρ) (f) .
Следовательно, для ρ = Π
0
(τ) получаем
Π
0
(τ) (f
3
(x)) = Π
000
(Π
0
(τ)) (f) .
Итак,
τ (f
1
(x)) = Π
000
(Π
0
(τ)) (f) .
Аналогичным образом можно доказать, что
τ (f
2
(x)) = Π
000
(Π
00
(τ)) (f) .
Поэтому,
Π
˜
f
(τ)
˜
f
=
Π
000
(Π
0
(τ)) (f) , если τ |= T ;
Π
000
(Π
00
(τ)) (f) , если τ 6|= T ;
не определено, если τ (T ) не определено.
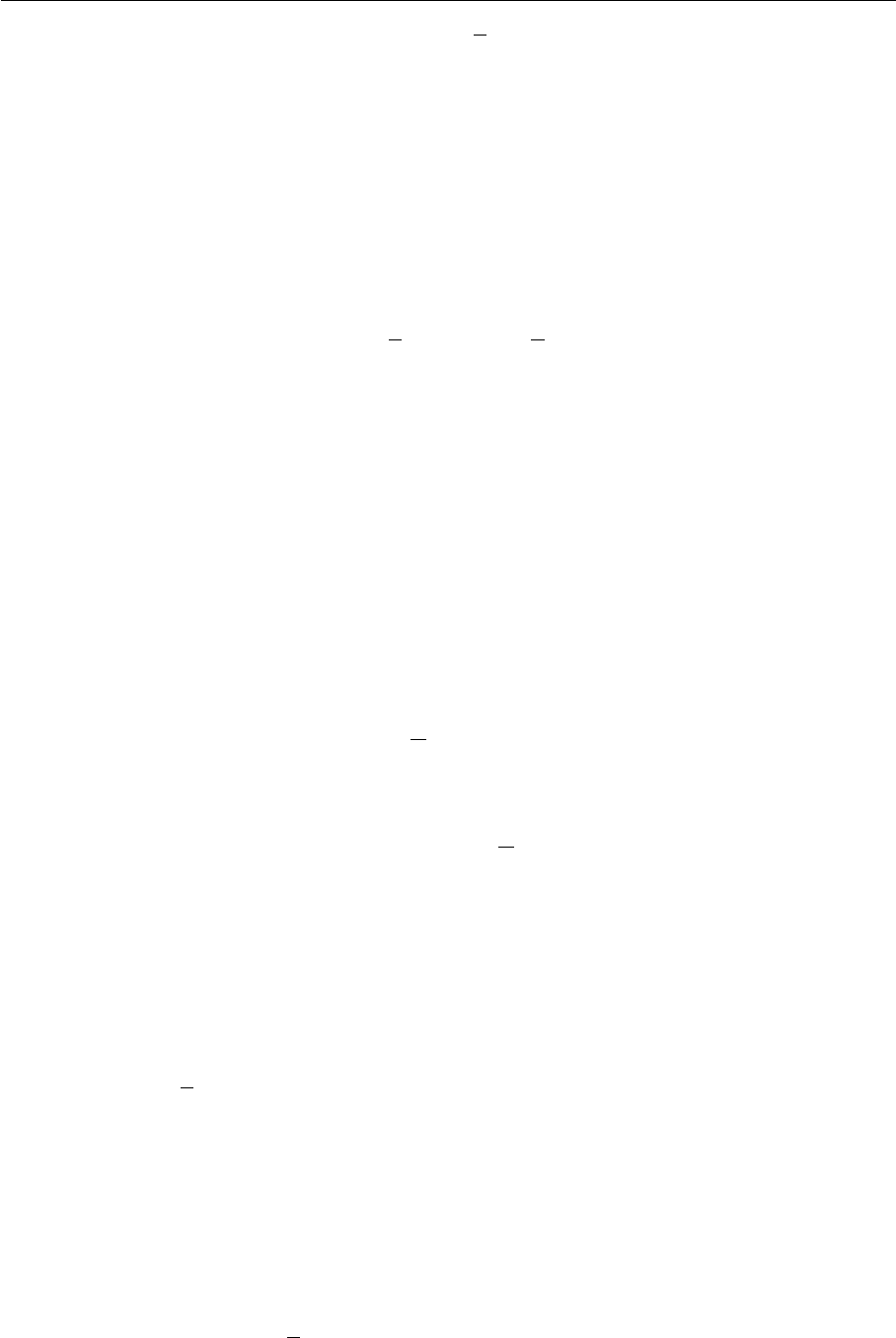
6.3.
∗
Аппликативное и функциональное программирование 167
Подойдем с другой стороны: σ (f (e)) = Π
f
(τ) (f). По определению
семантики для ветвления и для следования, получаем:
Π
f
(τ) (f) =
Π
000
(Π
0
(τ)) (f) , если τ |= T ;
Π
000
(Π
00
(τ)) (f) , если τ 6|= T ;
не определено, если τ (T ) не определено.
Как видим, получилось то же самое, то есть
σ (f (e)) = σ
˜
f (e)
для всякого состояния σ.
Вес был равен
w = 2 (w (Π
0
) + w (Π
00
)) + 2w (Π
000
) + 1,
стал равен:
w (Π
0
) + w (Π
00
) + w (Π
000
) .
4. Заменим всюду f на
˜
f:
Sub
˜
f;
arg x;
if T then
Π
0
u =
˜
f (x) ;
else
Π
00
end;
˜
f = u;
end;
Пусть τ (f (e)) определено. Пусть
δ = (f, τ (e
1
) , . . . , τ (e
n
)) .
Значит последовательность состояний цикла
σ
i
n
i=0
: σ
0
= σ
δ
, σ
i+1
=
Π
0
σ
i
является конечной, Π
0
σ
i
определено для всех i < n и σ
i
|= T
тогда и только тогда, когда i < n. Следовательно,
τ (f (e)) = Π
00
(σ
n
) (u) = Π
f
(σ
n
) (f) ,

168 Глава 6. Подпрогра ммы, функциональное программирование
так как σ
n
6|= T .
Индукцией по n − i докажем, что Π
˜
f
σ
i
определено и
Π
˜
f
σ
i
˜
f
= Π
f
(σ
n
) (f) .
Базис индукции.
Если n = i, то σ
i
6|= T и, следовательно,
Π
˜
f
σ
i
˜
f
= Π
00
σ
i
(u) = Π
f
σ
i
(u) = Π
f
(σ
n
) (f) .
Шаг индукции.
Пусть для i + 1 утверждение доказано и i < n. Тогда σ
i
|= T .
Π
˜
f
σ
i
= Π
0
σ
i
˜
f (x)
= σ
i+1
˜
f (x)
= Π
˜
f
σ
i+1
˜
f
.
По индукционному предположению порлучаем, что
Π
˜
f
σ
i+1
˜
f
= Π
f
(σ
n
) (f) .
Итак, мы доказали, что
Π
˜
f
σ
0
˜
f
= Π
f
(σ
n
) (f) .
Но σ
0
= σ
δ
, поэтому
τ
˜
f (e)
= Π
˜
f
(σ
δ
)
˜
f
= Π
f
(σ
n
) (f) = τ (f (e)) .
Пусть τ
˜
f (e)
определено. Пусть
δ = (f, τ (e
1
) , . . . , τ (e
n
)) .
Рассмотрим последовательность состояний цикла
σ
i
i
: σ
0
= σ
δ
, σ
i+1
=
Π
0
σ
i
.
Индукцией по i покажем, что если σ
j
|= T для j ≤ i, то Π
˜
f
σ
i
определено и
Π
˜
f
σ
i
˜
f
= Π
˜
f
(σ
δ
)
˜
f
.
Базис индукции.
Для i = 0 это следует из определенности τ
˜
f (e)
.
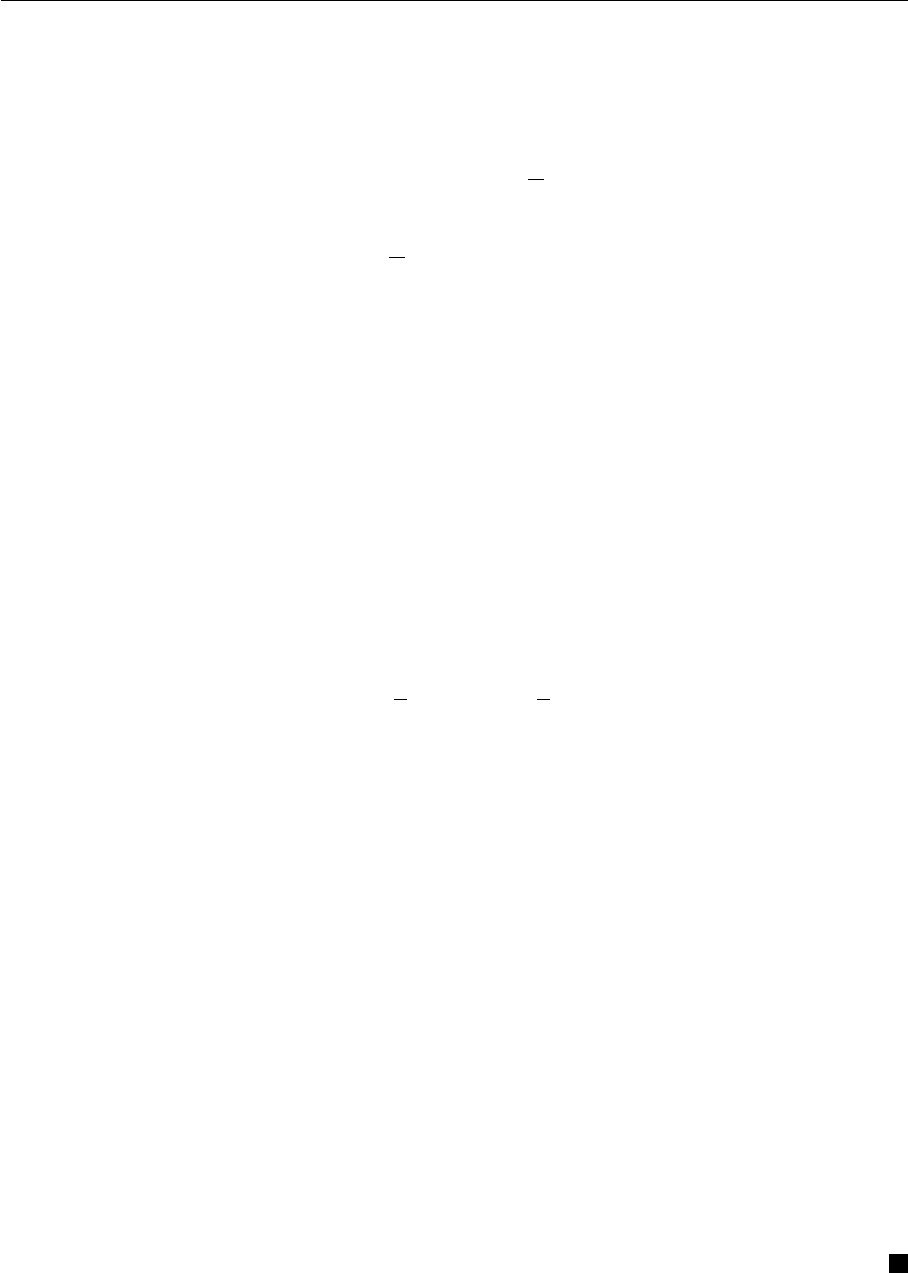
6.3.
∗
Аппликативное и функциональное программирование 169
Шаг индукции.
Пусть для i утверждение доказано. Пусть σ
j
|= T для j ≤ i + 1. Рас-
смотрим Π
˜
f
σ
i
. Так как σ
i
|= T , то
Π
˜
f
σ
i
˜
f
=
˜
f = u;
u =
˜
f (x) ;
Π
0
σ
i
˜
f
=
= σ
i+1
˜
f (x)
= Π
˜
f
σ
i+1
˜
f
,
что и требовалось. Более того, мы доказали, что если σ
i
|= T , то для
определения Π
˜
f
σ
i
необходимо определить Π
˜
f
σ
i+1
.
Так как Π
˜
f
σ
0
определено, то такая цепь не может быть бесконечной,
следовательно, σ
n
6|= T для некоторого n. Тогда
Π
f
(σ
δ
) (f) = Π
00
(σ
n
) (u) .
С другой стороны
Π
˜
f
(σ
δ
) (f) = Π
00
(σ
n
) (u) ,
то есть Π
f
(σ
δ
) должно быть определено. Из этого следует, что
τ
˜
f (e)
= τ (f (e)) .
Вес был:
w (Π
f
) = 2 + 2w (Π
0
) + 2
w(Π
0
)+1
+ 2w (Π
00
) + 1 + 1,
стал:
w
Π
˜
f
≤ 1 + 2
w (Π
0
) + 1 + 2
w(Π
0
)
+ 2w (Π
00
) < w (Π
f
) .
Будем производить преобразования 1–4, пока они приводят к умень-
шению w (A).
Если w (A) = 0, то тело каждой подпрограммы f либо является при-
сваиванием вида f = e; либо является полным ветвлением, частями
которого снова являются или присваивания такого вида, или операторы
полного ветвления. Следовательно, такой алгоритм является функцио-
нальным.
∗
Задача 6.16. Покажите, как убрать неполное ветвление и докажи-
те правильность предложенного построения.

170 Глава 6. Подпрогра ммы, функциональное программирование
Как мы видим, передача аргументов заменяет присваивание, а рекур-
сивный вызов — оператор цикла.
Задача 6.17. Пользуясь методом из теоремы, по алгоритмам из за-
дачи 6.2 на стр. 151 постройте эквивалентные им функциональные.
Лемма 6.7. Если у нас есть операция IF (x, y, z), аргументами кото-
рой являются x — тест, y, z — выражения, такая, что для всякого
состояния σ
σ (IF (x, y, z)) =
σ (y) , если σ |= x,
σ (z) , если σ 6|= x,
не определено, если σ (x) не определено,
то программа вида
if T then
f = e
1
;
else
f = e
2
;
end;
эквивалентна программе
f = IF (T, e
1
, e
2
) ;
Задача 6.18. Докажите лемму.
Теперь мы можем показать, что при наличии операции IF , функцио-
нальная программа оправдывает свое название:
Следствие 6.5. Если у нас есть операция IF (x, y, z) (см. предыдущую
лемму), то каждый алгоритм эквивалентен функциональному, в ко-
тором каждая подпрограмма и основная программа имеет тело вида:
f = e;
где f — имя подпрограммы или алгоритма соответственно.
Задача 6.19. Докажите следствие.
Замечание 6.3. Покажем, что изменив понятия истинности и лож-
ности можно избавиться и от IF . Будем считать, что исти-
на — это двухместная операция, возвращающая первый аргумент, а
