Дуброва Т.А. Статистические методы прогнозирования в экономике

Подождите немного. Документ загружается.

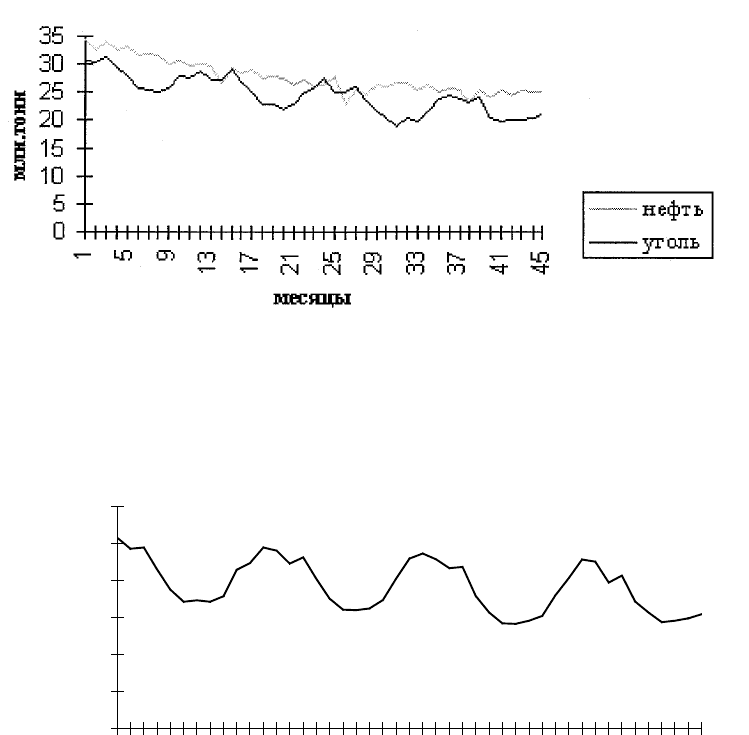
Рисунок 1.2. Месячная динамика производства

отдельных видов промышленной продукции

в натуральном выражении

Рисунок 1.3. Месячная динамика производства

электроэнергии

100

120

Месяцы

млрд.квт.ч.

На рисунках 1.2, 1.3 приведены примеры временных рядов, иллюстрирующие

присутствие в них указанных компонент. Графики месячных временных рядов

производства промышленной продукции наглядно демонстрируют устойчивые

сезонные колебания при снижающемся тренде, причем на последнем участке темпы

падения производства заметно снижаются.

Решение любой задачи по анализу и прогнозированию временных рядов

начинается с построения графика исследуемого показателя, тем более, что

современные программные средства предоставляют пользователю большие

возможности для этого. Не всегда при этом четко прослеживается присутствие

тренда во временном ряду. В этих случаях прежде, чем перейти к определению

тенденции и выделению тренда, нужно выяснить, существует ли вообще тенденция в

исследуемом процессе.

Основные подходы к решению этой задачи основаны на статистической

проверке гипотез. Критерии выявления компонент ряда основаны на проверке

гипотезы о случайности ряда.

Рассмотрим наиболее часто используемые на практике критерии проверки

"наличия-отсутствия" тренда: критерий серий, основанный на медиане выборки и

метод Фостера - Стюарта.

Критерий серий, основанный на медиане выборки,реализуется в виде

следующей последовательности шагов:

1) Из исходного ряда y

длиной n образуется ранжированный (вариационный)

ряд y

: y , y , ... , y

, где y

- наименьшее значение ряда y

2) Определяется медиана этого вариационного ряда Me. В случае нечетного

значения n (n=2m+1) Me=y

, в противном случае Me=

()

yy:2

3) Образуется последовательность d i из плюсов и минусов по следующему

правилу:

n , ... 2, 1,= tMe,y если ,

n, ... 2, 1,= tMe,y если ,

d (1.4.)

Если значение y

равно медиане, то это значение пропускается.

4) Подсчитывается

n(n) -число серий в совокупности d

, где под серией

понимается последовательность подряд идущих плюсов или минусов. Один плюс

или один минус тоже будет считаться серией.

Определяется

max

(n)- протяженность самой длинной серии.

5) Проверка гипотезы основывается на том, что при условии случайности ряда

(при отсутствии систематической составляющей) протяженность самой длинной

серии не должна быть слишком большой, а общее число серий - слишком маленьким.

Поэтому для того, чтобы не была отвергнута гипотеза о случайности исходного ряда

(об отсутствии систематической составляющей) должны выполняться следующие

неравенства (для 5% уровня значимости)

(

)

(

)

[]

()

max

n3,3lgn1

n 1 1,96 n 1

>+- -

(1.5.)

Если хотя бы одно из неравенств нарушается, то гипотеза об отсутствии

тренда отвергается.

Квадратные скобки в правой части неравенства означают целую часть числа.

Напомним, что целая часть числа A - [A] - это целое число, ближайшее к А и не

превосходящее его.

Другой способ проверки гипотезы о наличии тенденции процесса

основывается на методе Фостера-Стюарта. Этот метод может быть реализован в виде

следующей последовательности шагов:

1) Каждый уровень ряда сравнивается со всеми предшествующими, при этом

определяются значения вспомогательных характеристик m

и l

случае противном в 0,

y , ... ,y ,yy если 1,

12-t1tt

(1.6.)

Таким образом, m

=1, если y

больше всех предшествующих уровней, а1

=1,

если y

меньше всех предшествующих уровней.

2) Вычисляется d

-l

для всех t=2¸n.

Очевидно, что величина d

может принимать значения 0; 1; -1.

3) Находится характеристика

4) С помощью критерия Стьюдента проверяется гипотеза о том, что можно

считать случайной разность D-0 (т.е. ряд можно считать случайным, не содержащим

тренд).

Для этого определяется

наб л

где

- средняя квадратическая ошибка величины D:

2 ln n 0,8456=»-

Значения s

затабулированы.

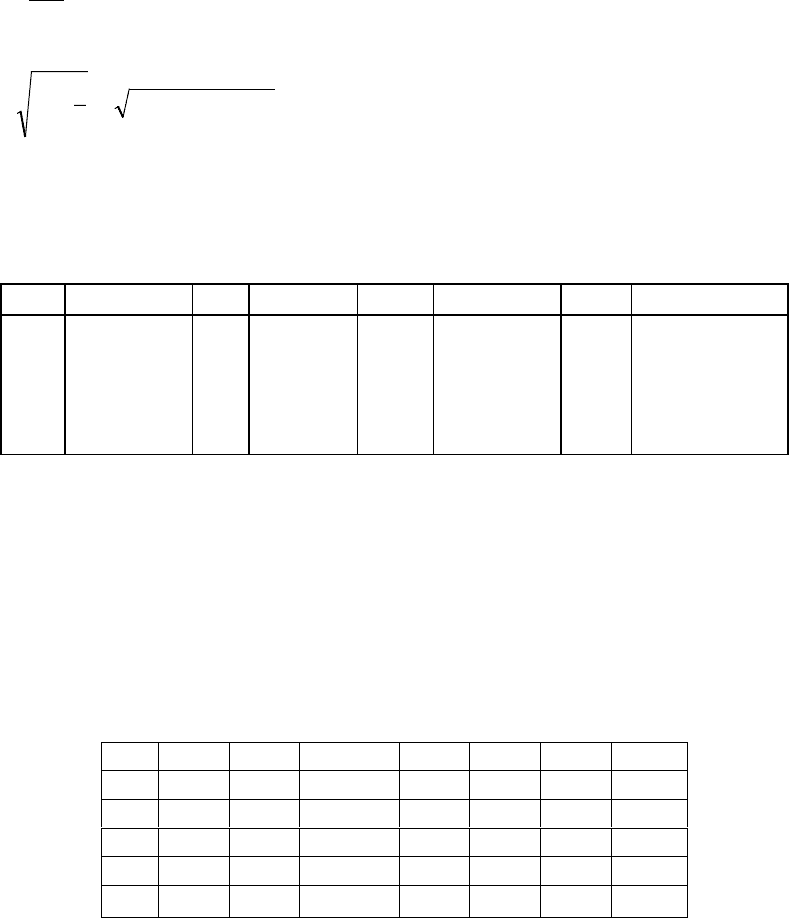
Таблица 1.2.

Значения стандартных ошибок для s

для n от 10 до 100

1,964

2,153

2,279

2,373

2,447

2,509

2,561

2,606

2,645

2,681

2,713

2,742

2,769

2,793

2,816

100

2,837

2,857

2,876

2,894

Расчетное значение t

набл

сравнивается с критическим значением t

кр

, взятым из

таблицы t-распределения Стьюдента для заданного уровня значимости

a и числа

степеней свободы k = n - 1. Если

êt

набл

ê > t

кр

, то гипотеза об отсутствии тренда

отвергается.

Пример 1.1.

Изменения курса акций промышленной компании в течение месяца

представлены в таблице:

Курс акций (дол.)

1 509 6 515 11 517 16 510

2 507 7 520 12 524 17 516

3 508 8 519 13 526 18 518

4 509 9 512 14 519 19 524

5 518 10 511 15 514 20 521

Проверить утверждение об отсутствии тенденции в изменении курса акций

двумя способами:

а) с помощью метода Фостера - Стюарта;

б) используя критерий серии, основанный на медиане выборки.

Доверительную вероятность принять равной 0,95.

Решение

а) Вспомогательные вычисления по методу Фостера- Стюарта представлены в

таблице 1.3.

Если уровень y

больше всех предшествующих уровней, то в графе m

ставим 1,

если y

меньше всех предшествующих уровней, то ставим 1 в графе l

;

Определяем d

-l

для t=2¸20;

Dd3

;

Значение s

для n=20 берем из таблицы 1.2.

=2,279.

Значение t

кр

берем из таблицы t- распределения Стьюдента:

кр

(a=0,05; К=19)=2,093;

1 316,

кр

Þ нет оснований отвергнуть гипотезу об отсутствии тренда.

С вероятностью 0,95 тренд во временном ряду отсутствует.

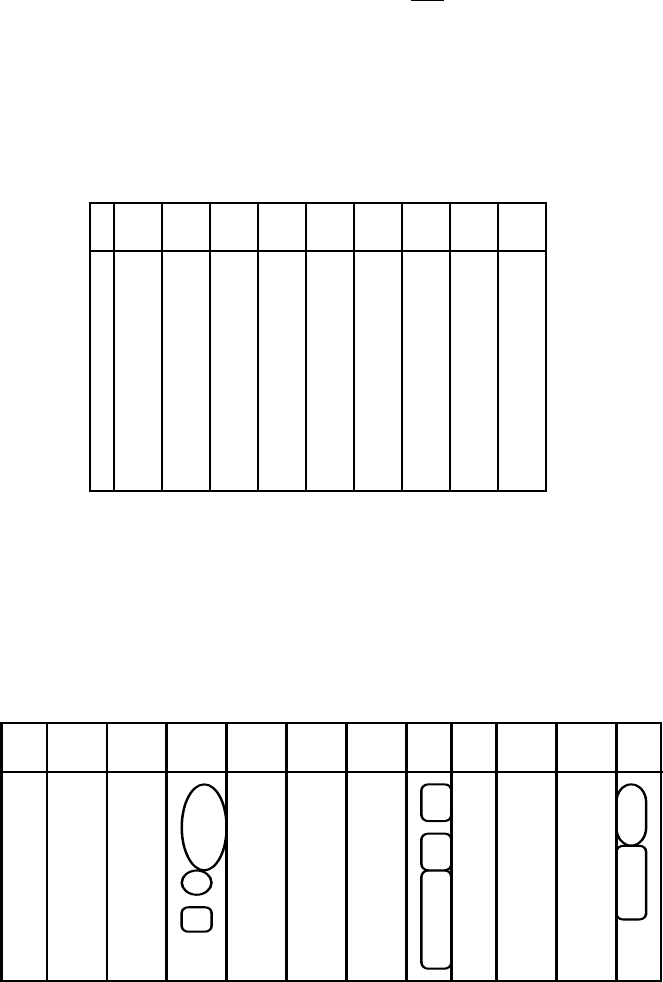
Таблица 1.3.

Вспомогательные вычисления по методу Фостера-Стюарта

t t

509

507

508

509

518

515

520

519

512

511

517

524

526

519

514

510

516

518

524

521

б) Проверим гипотезу об отсутствии тенденции в изменении курса акций с

помощью критерия серий, основанного на медиане выборки.

Вспомогательные вычисления представлены в таблице 1.4.

Таблица 1.4.

Вспомогательные вычисления для критерия серии

t y

509

507

508

509

518

515

507

508

509

510

511

520

519

512

511

517

524

526

519 +

512

514

515

516

517

518

519

514

510

516

518

524

521

519

520

521

524

526

1) От исходного ряда y

переходим к ранжированному y

, расположив значения

исходного ряда в порядке возрастания;

2) Т. к. n=20 (четное)

Þ медиана Me

516,5

= ;

3) Значение каждого уровня исходного ряда y

сравнивается со значением

медианы. Если y

>Me, то d

принимает значение «+», если меньше, то»-»;

n (20)=8- число серий;

t max

(20)=4- протяженность самой большой серии.

В соответствии с (1.7.) делаем проверку:

()

[]

()

max

(20) , lg

(20) ,

>+- -

33 20 1

20 1 196 20 1

4<7

8>6

Оба неравенства выполняются. С вероятностью 0,95 тренд во временном ряду

отсутствует, что согласуется с выводом, сделанным с помощью метода Фостера-

Стюарта.

Глава 2. Основные показатели динамики экономических явлений.

Использование скользящих средних для сглаживания временных рядов

§ 2.1. Основные показатели динамики экономических явлений

Для количественной оценки динамики явлений применяются статистические

показатели: абсолютные приросты, темпы роста, темпы прироста, причем они могут

разделяться на цепные, базисные и средние.

В основе расчета этих показателей динамики лежит сравнение уровней

временного ряда. Если сравнение осуществляется с одним и тем же уровнем,

принятым за базу сравнения, то эти показатели называются базисными. Если

сравнение осуществляется при переменной базе, и каждый последующий уровень

сравнивается с предыдущим, то вычисленные таким образом показатели называются

цепными.

Абсолютный прирост

Dу равен разности двух сравниваемых уровней.

Темп роста Т характеризует отношение двух сравниваемых уровней ряда,

выраженное в процентах.

Темп прироста К характеризует абсолютный прирост в относительных

величинах. Определенный в % темп прироста показывает, на сколько процентов

изменился сравниваемый уровень по отношению к уровню, принятому за базу

сравнения. В таблице 2.1. приведены выражения для вычисления базисных и цепных

приростов, темпов роста, темпов прироста. При этом использованы следующие

обозначения:

, ... ,y

- уровни временного ряда t=1, 2, ... , n;

n- длина временного ряда;

-уровень временного ряда, принятый за базу сравнения.

Таблица 2.1.

Основные показатели динамики

Прирост Темп роста Темп прироста

Цепной

Dу

-y

t-1

100%

=´

-100%

Базисный

-y

100%

=´

КТ100%

бб

Средний

Dy =

100%

=´

КТ100%=-

Для получения обобщающих показателей динамики развития определяются

средние величины: средний абсолютный прирост, средний темп роста и прироста.

Описание динамики ряда с помощью среднего прироста соответствует его

представлению в виде прямой, проведенной через две крайние точки. В этом случае,

чтобы получить прогноз на один шаг вперед, достаточно к последнему наблюдению

добавить значение среднего абсолютного прироста.

)

yD+=

+ n1n

y (2.1.),

где y

- фактическое значение в последней n- ой точке ряда;

)

1n+

-прогнозная оценка значения уровня в точке n+1;

Dy - значение среднего прироста, рассчитанное для временного ряда y

, ... ,y

Очевидно, что такой подход к получению прогнозного значения корректен,

если характер развития близок к линейному. На такой равномерный характер

развития могут указывать примерно одинаковые значения цепных абсолютных

приростов.

Применение среднего темпа роста ( и среднего темпа прироста) для описания

динамики ряда соответствует его представлению в виде показательной или

экспоненциальной кривой, проведенной через две крайние точки. Поэтому

использование этого показателя в качестве обобщающего целесообразно для тех

процессов, изменение динамики которых происходит примерно с постоянным

темпом роста. В этом случае прогнозное значение на i шагов вперед может быть

получено по формуле:

)

nin

Тy ´=

(2.2.),

где

)

in +

- прогнозная оценка значения уровня в точке n+i;

- фактическое значение в последней n-ой точке ряда;

Т - средний темп роста, рассчитанный для ряда y

, ... ,y

(не в % выражении).

К недостаткам среднего прироста и среднего темпа роста следует отнести то,

что они учитывают лишь конечный и начальный уровни ряда, исключают влияния

промежуточных уровней. Тем не менее, эти показатели имеют весьма широкую

область применения, что объясняется чрезвычайной простотой их вычисления. Они

могут быть использованы как приближенные, простейшие способы прогнозирования,

предшествующие более глубокому количественному и качественному анализу.

§ 2.2. Сглаживание временных рядов с помощью скользящей средней

Распространенным приемом при выявлении тенденции развития является

сглаживание временного ряда. Суть различных приемов сглаживания сводится к

замене фактических уровней временного ряда расчетными уровнями, которые

подвержены колебаниям в меньшей степени. Это способствует более четкому

проявлению тенденции развития. Иногда сглаживание применяют как

предварительный этап перед использованием других методов выделения тенденции

(например, рассматриваемых в третьей главе).

Скользящие средние позволяют сгладить как случайные, так и периодические

колебания, выявить имеющуюся тенденцию в развитии процесса, и поэтому,

являются важным инструментом при фильтрации компонент временного ряда.

Алгоритм сглаживания по простой скользящей средней может быть

представлен в виде следующей последовательности шагов:

1. Определяют длину интервала сглаживания g, включающего в себя g

последовательных уровней ряда (g<n). При этом надо иметь в виду, что чем шире

интервал сглаживания, тем в большей степени взаимопогашаются колебания, и

тенденция развития носит более плавный, сглаженный характер. Чем сильнее

колебания, тем шире должен быть интервал сглаживания.

2. Разбивают весь период наблюдений на участки, при этом интервал

сглаживания как бы скользит по ряду с шагом, равным 1.

3. Рассчитывают арифметические средние из уровней ряда, образующих

каждый участок.

4. Заменяют фактические значения ряда, стоящие в центре каждого участка, на

соответствующие средние значения.

При этом удобно брать длину интервала сглаживания g в виде нечетного

числа: g=2p+1, т.к. в этом случае полученные значения скользящей средней

приходятся на средний член интервала.

Наблюдения, которые берутся для расчета среднего значения, называются

активным участком сглаживания.

При нечетном значении g все уровни активного участка могут быть

представлены в виде:

t-p

, y

t-p+1

, ... , y

t-1

, y

t+1

, ... , y

t+p-1

, y

t+p

а скользящая средняя определена по формуле:

)

12p

yy...yy

12p

pt1pt1ptp-t

pti

++++

+-++-

(2.3.),

где y

- фактическое значение i-го уровня;

)

- значение скользящей средней в момент t;

2p+1- длина интервала сглаживания.

Процедура сглаживания приводит к полному устранению периодических

колебаний во временном ряду, если длина интервала сглаживания берется равной

или кратной циклу, периоду колебаний.

Для устранения сезонных колебаний желательно было бы использовать

четырех- и двенадцатичленную скользящие средние, но при этом не будет

выполняться условие нечетности длины интервала сглаживания. Поэтому при четном

числе уровней принято первое и последнее наблюдение на активном участке брать с

половинными весами:

)

y...yyy...yy

1pt

1pti

ipt

pt1pt1tt1t1ptpt

+-=

+-++-+--

++++++++

(2.4.)

Тогда для сглаживания сезонных колебаний при работе с временными рядами

квартальной или месячной динамики можно использовать следующие скользящие

средние:

)

yyyy

2t1tt1t2t

++--

++++

= (2.5.)

)

y...y...yy

6t5tt5t6t

++--

++++++

(2.6.)

При использовании скользящей средней с длиной активного участка g=2p+1

первые и последние p уровней ряда сгладить нельзя, их значения теряются.

Очевидно, что потеря значений последних точек является существенным

недостатком, т.к. для исследователя последние "свежие" данные обладают

наибольшей информационной ценностью. Рассмотрим один из приемов,

позволяющих восстановить потерянные значения временного ряда. Для этого

необходимо:

1) Вычислить средний прирост на последнем активном участке

t-p

, y

t-p+1

, ... , y

t+p-1

, y

t+p

Dy =

tp tp

где g- длина активного участка;

tp+

- значение последнего уровня на активном участке;

tp-

- значение первого уровня на активном участке;

Dy -средний абсолютный прирост.

2) Получить P сглаженных значений в конце временного ряда путем

последовательного прибавления среднего абсолютного прироста к последнему

сглаженному значению.

Аналогичную процедуру можно реализовать для оценивания первых уровней

временного ряда.

Метод простой скользящей средней применим, если графическое изображение

динамического ряда напоминает прямую. Когда тренд выравниваемого ряда имеет

изгибы, и для исследователя желательно сохранить мелкие волны, применение

простой скользящей средней нецелесообразно.

Если для процесса характерно нелинейное развитие, то простая скользящая

средняя может привести к существенным искажениям. В этих случаях более

надежным является использование взвешенной скользящей средней.

При сглаживании по взвешенной скользящей средней на каждом участке

выравнивание осуществляется по полиномам невысоких порядков. Чаще всего

используются полиномы 2-го и 3-его порядка. Так как при простой скользящей

средней выравнивание на каждом активном участке производится по прямой

(полиному первого порядка), то метод простой скользящей средней может

рассматриваться как частный случай метода взвешенной скользящей средней.

Простая скользящая средняя учитывает все уровни ряда, входящие в активный

участок сглаживания, с равными весами, а взвешенная средняя приписывает каждому

уровню вес, зависящий от удаления данного уровня до уровня, стоящего в середине

активного участка.

Выравнивание с помощью взвешенной скользящей средней осуществляется

следующим образом.

Для каждого активного участка подбирается полином вида

)

...tataa

210t

+++= ,

параметры которого оцениваются по методу наименьших квадратов. При этом

начало отсчета переносится в середину активного участка. Например, для длины

интервала сглаживания g=5, индексы уровней активного участка будут следующими

i: -2, -1, 0, 1, 2.

Тогда сглаженным значением для уровня, стоящего в середине активного

участка, будет значение параметра a

подобранного полинома.

Нет необходимости каждый раз заново вычислять весовые коэффициенты при

уровнях ряда, входящих в активный участок сглаживания, т.к. они будут

одинаковыми для каждого активного участка. Причем при сглаживании по полиному

к-ой нечетной степени весовые коэффициенты будут такими же, как при

сглаживании по полиному (к-1) степени. В таблице 2.2. представлены весовые

коэффициенты при сглаживании по полиному 2-го или 3-го порядка ( в зависимости

от длины интервала сглаживания).

Так как веса симметричны относительно центрального уровня, то в таблице

использована символическая запись: приведены веса для половины уровней

активного участка; выделен вес, относящийся к уровню, стоящему в центре участка

сглаживания. Для оставшихся уровней веса не приводятся, т. к. они могут быть

симметрично отражены.

Например, проиллюстрируем использование таблицы для сглаживания по

параболе 2-го порядка по 5-членной взвешенной скользящей средней. Тогда

центральное значение на каждом активном участке y

t-2

, y

t-1

, y

t+1

, y

t+2

, будет

оцениваться по формуле:

)

()

2t1tt1t2tt

3y12y17y12y3y

++--

-+++-=

Отметим важные свойства приведенных весов:

1) Они симметричны относительно центрального уровня.

2) Сумма весов с учетом общего множителя, вынесенного за скобки, равна

единице.

3) Наличие как положительных, так и отрицательных весов, позволяет

сглаженной кривой сохранять различные изгибы кривой тренда.

Существуют приемы, позволяющие с помощью дополнительных вычислений

получить сглаженные значения для Р начальных и конечных уровней ряда при длине

интервала сглаживания g=2p+1.

Таблица 2.2.

Весовые коэффициенты при сглаживании по полиномам второго и

третьего порядка

Длина интервала

Сглаживания

Весовые коэффициенты

- ,+12,+17

236

-+++,,,7

231

21 14 39 54

-+ ++ +,,,,59

429

36 9 44 69 84

-+++++,, , , ,89

143

11 0 9 16 21 24

-+++++,, , , , , 25