Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

SECTION 8.8 FURTHER READING 239

= −



i=1

∗



∗

) ∧ v

= 0.

This kind of pulling out a differentiation operator is a good trick to remember. The result-

ing equation expresses the fact that R

∗

f[x]



∗

is a symmetric function of x. The function

f itself is therefore the



∗

-rotated version of a symmet rical function.

We could proceed symbolically with geometric algebra to ﬁnd the sy mmetric par t of R

∗

[f]

(by adding the adjoint

f[R

∗

] and dividing by two), and its inverse (using (4.16)), and tak-

ing that out of the function; what remains is then the rotation by the desired rotor. How-

ever, [36] at this point switches over to using numerical linear algebra. In linear algebra,

any linear function f has a polar decomposition in a symmetric function followed by an

orthogonal transformation, and this can be computed using the singular value decom-

position (SVD) of its mat rix [[f]] as

≡ [[ U]] [[ S]] [[ V]]

= ([[U]] [[ V]]

)([[V]] [[ S]] [[ V]]

Using this result, the matrix of the optimal rotation

∗

is [[ V]] [[ U]]

,where[[ U]] and [[ V]]

are derived from the SVD of [[f]] ≡



i=1

[[ u

]] [[ v

]]

. This rotation matrix is easily con-

verted back into the optimal rotor R

∗

, see Section 7.10.4.

This simple matrix computation algorithm is indeed the standard solution to the Pro-

crustes problem. In the usual manner of its derivation, formulated in terms of involved

matrix manipulations, one may have some doubts as to whether the SVD (with its inher-

ent use of the Frobenius metric on matrices) is indeed the optimal solution to origi-

nal optimization problem (which involved the Euclidean distance). In the formulation

above, the intermediate result (8.17) shows that this is indeed correct, and that the

SVD is merely used to compute the decomposition rather than to perform the actual

optimization.

From a purist point of view, it is of course a pity that the last part of the solution had

to revert temporarily to a matrix formulation to compute a rotor. We expect that appro-

priate numerical techniques will be developed soon completely within the framework of

geometric algebra.

8.8 FURTHER READING

The main reference for further reading on geometric calculus is the classic book by

Hestenes [33], which introduced much of it. It contains a wealth of material, including

an indication of how geometric calculus could be used to rephrase differential geometry.

His web site contains more material, including some new introductions such as [26].

The approach in Doran and Lasenby’s book [15] is tailored towards physicists, and it has

good and practical introductions to the techniques of geometric calculus. Read them for

directed integration theory. They are practitioners who use it daily, and they give just the

right amount of math to get applicable results.

240 GEOMETRIC DIFFERENTIATION CHAPTER 8

8.9 EXERCISES

8.9.1 DRILLS

1. Compute the radius of the tangent circle for the circular motion

r(τ) = exp(−Iτ) e

in the plane I = e

∧ e

, at the general location r(τ).

2. Compute the following derivatives:

1. (a ∗

∂

) x

2. ∂

3. (a ∗ ∂

)(xb/x)

∂

(xb/x)

∂

x ∧

∂

x ·

∂

3. Show that the coordinate vectors are related to differentiation through e

∂

∂x

4. Show that the reciprocal frame vectors are the gradients of coordinate functions:

= ∂

8.9.2 STRUCTURAL EXERCISES

1. Prove the Jacobi identity (8.2) and relate it to nonassociativity of the bivector

algebra.

2. Derive the Taylor expansion of a rotor transformation:

−B/2

B/2

= X + X x B +

((X x B) x B) + ···.

Do this by assuming that the ﬁrst-order term is correct for small bivectors, it is eas-

ily derived by setting exp(−B/2) ≈ 1 − B/2. Now write a versor involving a ﬁnite

B as versors involving B/2, B/4, B/8, and so on and build up the total form through

repeated application of the smallest bivector forms. That should give the full

expansion.

3. The Baker-Campbell-Hausdorff formula writes the product of two exponentials as

a third, and gives a series expansion of its value:

= e

with

C = A + B + A

x B +

(A x (A x B) + B x (B x A)) + ···.

Show that these ﬁrst terms of the ser ies are correct. This formula again shows the

importance of the commutator A

x B in quantify ing the difference with fully com-

muting variables. We should warn you that the general terms of the series are more

complicated than the ﬁrst few suggest.

SECTION 8.9 EXERCISES 241

⎜⎜x⎜⎜

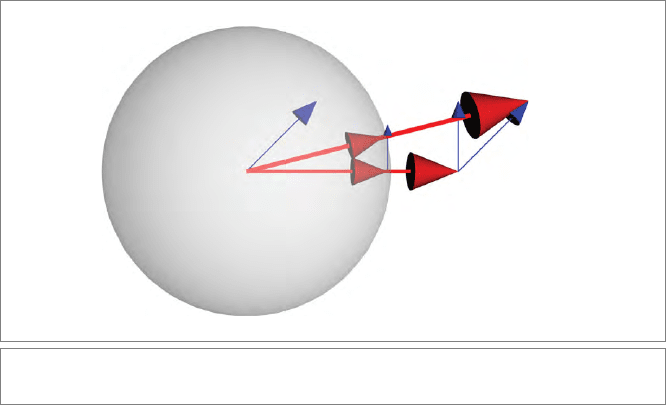
Figure 8.3: The directional derivative of the spherical projection.

4. Directional differentiation of spherical projection.

Suppose that we project a vector x on the unit sphere by the function x → P[x] =

x/||x||. Compute its directional derivative in the a direction, as a standard differ-

ential quotient using Taylor series expansion. Use geometric algebra to write the

result compactly, and give its geometric meaning. (Hint: See Figure 8.3.)

5. Justify the following form of Taylor’s expansion formula of a function F around the

location x:

F(x + a) = e

a∗∂

F(x),

where you can interpret the exponent in a natural manner as a symbolic expansion

instruction.

6. For variable I(τ), the resulting

∂

X(τ) of (8.8) can still be written as a commutator

x B with a bivector B. Derive the explicit expression for B:

B = I

∂

[␾] +

∂

[I](e

I␾

− 1)/I.

Hint: One way is to use the result B = −2

∂

[R]



R from [15].

MODELING GEOMETRIES

So far we have been treating only homogeneous subspaces of the vector spaces (i.e.,

subspaces containing the origin). We have spanned them, projected them, and rotated

them, but we have not moved them off the origin to make more interesting geometri-

cal structures such as lines ﬂoating in space. You might fear that we need to extend our

framework considerably to incorporate such new geometr ical elements and their algebra,

introducing offset blades as algebraic primitives.

However, signiﬁcant extensions turn out to be unnecessary, by using a simple trick that

is a lot more generic than it appears at ﬁrst: these offset elements of geometry in a vector

space

can also be represented by blades, but in a representational space R

n+1

with

one extra dimension. The geometric algebra of that space then gives us most of what

we need to compute in

. Since the blades of that higher-dimensional space R

n+1

are

its homogeneous subspaces, this is called the homogeneous model of geometry (though

“homogenized” might be more accurate, for we have made things homogeneous in

n+1

that were not in R

In this view, more complicated geometrical objects do not require new operations or tech-

niques in geometric algebra, merely the standard computations in a higher-dimensional

space, followed by an interpretation step. The geometric algebra approach considerably

extends the classical techniques of homogeneous coordinates, so it pays to redevelop this

fairly well-known material. The homogeneous model permits us to represent offset

subspaces as blades, and transformations on them as linear transformations and their

outermorphisms. As we develop the details in Chapter 11, we ﬁnd that the geometric

245

246 MODELING GEOMETRIES CHAPTER 9

algebra approach exposes some weaknesses in the homogeneous model. It turns out that

we cannot really deﬁne a useful inner product in the representation space

n+1

that

represents the metric aspects of the original space

well; we can only revert to the

inner product of

. As a consequence, we also have no compelling geometric product,

and our geometric algebra of

n+1

is impoverished, being reduced to outer product and

nonmetric uses of duality (such as

meet and join). This restr icts the natural use of the

homogeneous model to applications in which the metric is less important than the aspects

of spanning and intersection. The standard example is the projective geometry involved

in imaging by multiple cameras, and we treat that application in detail in Chapter 12. Still,

the quantitative capabilities of geometric algebra do help in assigning some useful relative

metrical meaning to ratios of computed elements.

The better model to treat the metric aspects of Euclidean geomet ry is a representation

that can make full use of the power of geometric algebra. That is the conformal model

of Chapter 13, which requires two extra dimensions. It provides an isometric model of

Euclidean geometry. In this representation, all Euclidean transformations become repre-

sentable as versors, and are therefore manifestly structure-preserving. This gives a satis-

fyingly transparent structure for dealing with objects and operators, far transcending the

classical homogeneous coordinate techniques. We initially show how this indeed extends

the homogeneous model with metric capabilities, such as the smooth interpolation of

rigid body motions in Chapter 13. Then in Chapter 14 we ﬁnd that there are other

elements of Euclidean geometry naturally represented as blades in this model: spheres,

circles, point pairs, and tangents. These begin to suggest applications and algorithms that

transcend the usual methods. To develop the tools for those, we look at the new construc-

tions in detail in Chapter 15. In the last chapter on the conformal model, we ﬁnd the

reason behind its name: all conformal (angle-preserving) transformations are versors,

and this now also gives us the possibility to smoothly interpolate rigid body motions with

scaling. In all of these chapters, the use of the interactive software is important to convey

how natural and intuitive these new tools can become.

But ﬁrst, we should make more explicit how the regular n-dimensional geometric alge-

bra, used as a vector space model, gives us tools to treat the directional aspects of an

n-dimensional space. This capability of computing with an algebra of directions will

transfer to the more powerful models as a directional submodel at every location in space.

THE VECTOR SPACE

MODEL: THE ALGEBRA

OF DIRECTIONS

When we developed geometric algebra in the ﬁrst part of this book, we illustrated the

principles with pictures in which vectors are represented as arrows at the origin, bivectors

as area elements at the origin, and so on. This is the purest way to show the geometric

properties corresponding to the algebra.

The examples showed that you can already use this algebra of the mathematical vector

space

to model useful aspects of Euclidean geometry, for it is the algebra of directions

of n-dimensional Euclidean space. We explore some more properties of this model in this

chapter, with special emphasis on computations with directions in 2-D and 3-D. Most

topics are illustrated with programming exercises at the end of the chapter.

First we show how the vector space model can be used to derive fundamental results in the

mathematics of angular relationships. We give the basic laws of trigonometry in the plane

and in space, and show how rotors can be used to label and classify the crystallographic

point groups.

Then we compute with 3-D rotations in their rotor representation, establishing some

straightforward techniques to construct a rotor from a given geometrical situation, either

deterministically or in an optimal estimation procedure. The logarithm of a 3-D rotor

enables us to interpolate rotations.

247

248 THE VECTOR SPACE MODEL: THE ALGEBRA OF DIRECTIONS CHAPTER 10

Finally, we give an application to external camera calibration, to show how the vector

space model can mix directional and locational aspects.

10.1 THE NATURAL MODEL FOR DIRECTIONS

There are n independent 1-D directions in an n-dimensional physical space, and they can

conveniently be drawn as vectors at the origin. Mathematically, they form a vector space

, for they can be added and scaled with real numbers to produce other legitimate 1-D

directions. The metric of the directions in the physical space (typically Euclidean) can be

used to induce a metric in this mathematical representation. That gives a model of the

directions in physical space in terms of the geometric algebra of a metric vector space

The vector space model thus constructed is indeed a good computational representation of

spatial directions at the origin. We have used it in all our illustrations of the geometrical

properties of geometric algebra in Part I. This already gave a list of powerful abilities,

directly applicable to computations with directions. We list the main results.

•

The k-dimensional directions in n-dimensional space can be composed as outer

products of k 1-D directions (represented as vectors). These k-blades can be decom-

posedonan





-dimensional basis. Only for grades 0, 1, (n−1), and n can k-blades

be constructed by arbitrary addition of basis elements.

•

Directions have an attitude, a weight, and an orientation.

•

Relative angles between k-dimensional directions can be computed using the con-

traction, even when they are of different grades. A k-direction can be represented

by its dual, the direction of its orthogonal complement.

•

Intersection and union of k-directions is deﬁned by meet and join,whicharea

speciﬁc combination of outer product and duality. The orthogonal projection of

k-directions is also well deﬁned by the contraction.

•

Directions can be used to reﬂect other directions using sandwiching products

(where some care is required to process their orientation properly).

•

Directions can be rotated using rotors and multiplied by the geometric product to

produce such rotors.

Beyond these structural properties, true for the abstract directions of a general vector

space

, we need speciﬁc techniques to use the blades of the vector space model to solve

particular geometrical problems, notably in the Euclidean spaces

and R

10.2 ANGULAR RELATIONSHIPS

The vector space model is the natural model to treat angular relationships at a single

location. To show this, we derive the elementary laws of sines and cosines in a

SECTION 10.2 ANGULAR RELATIONSHIPS 249

planar triangle; some similar relationships in a spherical triangle; and the point groups

of crystallography. The results are not new, but intended as examples of how you can

now think about such problems in a purely directional manner using geometric algebra.

Especially the ability to divide and multiply vectors will simplify both the computations

and the deﬁnition of the oriented angular parameters in the conﬁgurations.

10.2.1 THE GEOMETRY OF PLANAR TRIANGLES

The combination of rotors in the same plane is sufﬁcient to derive the various relation-

ships between sides and angles in triangles. We repeat the derivation of these laws as given

in [29], pp. 68–70, since this application shows the simplicity and power of geometric

algebra nicely. Quantities that are required to characterize the properties are completely

deﬁnable in terms of the original elements of the problem.

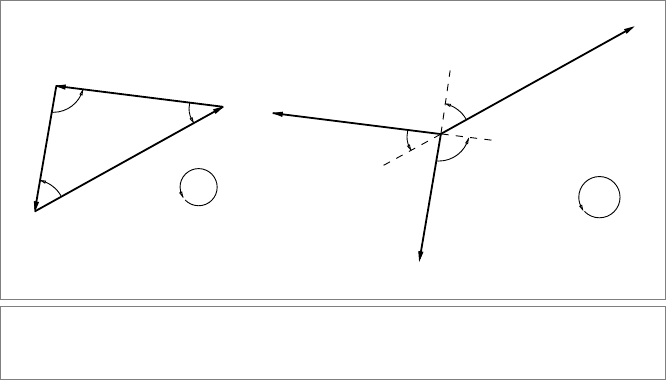
In Figure 10.1(a) we have indicated a triangle in the 2-D Euclidean I-plane, composed of

three vectors a, b, c that have the relationship

a + b + c = 0.

(10.1)

These vectors indicate weighted directions, and their weights can be drawn as their

lengths. Although they have been drawn offset from the origin, there are no actual posi-

tional aspects to this triangle and its relationships. This is shown by redrawing all vectors

involved as emanating from the origin, in a purist version of the triangle, as Figure 10.1(b).

The relevant geometric algebra of both ﬁgures is the same.

(a) (b)

Figure 10.1: A triangle a + b + c = 0 in a directed plane I, and an equivalent conﬁguration for

treatment with the vector space model.

250 THE VECTOR SPACE MODEL: THE ALGEBRA OF DIRECTIONS CHAPTER 10

Solving this equation a + b + c = 0 for c, and squaring, we get

= (a + b)

= a

+ b

+ ab + ba = a

+ b

+ 2a · b. (10.2)

We may introduce the angle α between c and −b (in that order), and similarly β and γ

(see Figure 10.1), and we can introduce the lengths of the sides a, b, and c.The

picture deﬁnes what is meant, but in geometric algebra we would rather deﬁne those

elements unambiguously as properties of the geometric ratios of the original vectors.

Section 6.1.6 gives the principle. Carefully observing the required angles and signs leads

to the exact deﬁnitions:

−b/a ≡b/ae

Iγ

, −c/b ≡c/be

Iα

, −a/c ≡a/ce

Iβ

(10.3)

Daring to make such deﬁnitions is a skill that you should master, for it is the transition

from the classical methods of thinking about angles (with the associated headaches on

the choice of signs) to the automated computations of geometric algebra. Make sure

you understand the precise relationship between these deﬁnitions and the ﬁgure they

represent!

When combined with the basic property (10.1), the angle deﬁnitions (10.3) fully deﬁne

all relationships in the triangle. It just takes geometrically inspired algebraic manipula-

tion to bring them out. For instance, we can multiply these equations. Remembering that

exponentials of commuting arguments are additive, we obtain by (10.3)

I(α+β+γ)

= e

Iα

Iγ

Iβ

= (−c/b)(−b/a)(−a/c) = −1 = e

Iπ

(10.4)

This implies that

α + β + γ = π mod (2π), (10.5)

which is a rather familiar result.

To obtain other classics, we split the geometric product in a contraction and an outer

product, thereby separating the equations into their scalar and bivector parts. This auto-

matically introduces the trigonometric functions as components of the rotors.

We multiply both sides of (10.3) by a

, and so on, and obtain six equations:

−b · a = ba cos γ, − b ∧ a = baI sin γ,

−c · b = cb cos α, − c ∧ b = cbI sin α,

−a · c = ac cos β, − a ∧ c = acI sin β.

Then the earlier results can be put into the classical form. Equation (10.2) is the law of

cosines:

c

= a

+ b

− 2ab cos γ.

(10.6)

SECTION 10.2 ANGULAR RELATIONSHIPS 251

Taking the outer product of (10.1) with a, b, and c, we obtain

a ∧ b = b ∧ c = c ∧ a, (10.7)

which leads to the law of sines in the I-plane:

sin α

a

sin β

b

sin γ

c

. (10.8)

We have divided out the plane I in which this holds to achieve this classical form. But in

fact, (10.7) is more speciﬁc and is valid in any plane I in n-dimensional space.

In the classical formulation, the area of the triangle is

absin γ (or a similar expres-

sion). We see that in the directed plane I, we can deﬁne the oriented area Δ of the triangle

naturally by the equivalent ratios

Δ=

a ∧ b

2 I

b ∧ c

2 I

c ∧ a

2 I

. (10.9)

This is a proper geometric quantity that relates the area to the orientation of the plane it

is measured in.

10.2.2 ANGULAR RELATIONSHIPS IN 3-D

In a 3-D Euclidean space, geometrical directions can be indicated by vectors or bivectors

(which are always 2-blades). The scalars and trivectors have trivial directional aspects and

are mostly used for their orientations and magnitudes.

Relative angles between the directional elements are fully represented by their geometric

ratios. Let us consider only unit elements, so that we can fully focus on the angles. Between

two unit directional elements, there are three possibilities:

•

Two Vec t o r s. The geometric ratio of two unit vectors u and v isarotorR = v/u.It

contains in its components both the rotation plane I and the relative angle ␾ of the

two vectors. These can be retrieved from the rotor as the bivector angle I␾, using

the logarithm function deﬁned below in Section 10.3.3. Note that only the product

of plane and angle is a well-deﬁned geometric quantity, since each separately has an

ambiguity of magnitude and orientation. In that sense, scalar angles are ungeomet-

rical and should be avoided in computations, since they necessitate the nongeomet-

rical choice of standard orientation for the I-plane. Since you probably only need

the angles to use them in a rotation operator anyway, you may as well keep their

bivector with their magnitude as a single bivector angle.

•

Two Bivectors (2-Blades). The geometric ratio of two unit 2-blades U and V also

deﬁnes a rotor R = V/U. This is most easily seen by introducing their normal

vectors u ≡ U

∗

= U/I

and v ≡ V

∗

= V/I

. Substituting gives R = V/U = v/u.

Therefore, this reduces to the previous case. The bivector angle between two