Doktorov E.V., Leble S.B. A Dressing Method in Mathematical Physics

Подождите немного. Документ загружается.

1.8 Matrix factorizations and integrable systems 19

it is realized as a transformation that could be interpreted as a shift along

an auxilia ry ax is, say t [419]. The next idea g oes back to the Moser theorem

[338] that states that a nondiagonal part of an initial matrix tends to zero

if this t-transition is considered. More exactly, if a ﬂow is generated by the

Hamiltonian

= −tr(M log M − M ) (1.70)

on (R

,ω), where ω =



i=1

∧dq

,then

(k)=M

,k=1, 2,... .

An important role in this theory is play ed by the Toda chain written in the

Flashka form

=[B(M),M], (1.71)

where M is a tridiagonal matrix

M =

⎛

⎜

⎝

0 .

n−1

⎞

⎟

⎠

(1.72)

and B(M) contains zeros at the diagonal:

B(M )=

⎛

⎜

⎝

0 −b

0 .

. −b

n−1

⎞

⎟

⎠

(1.73)

Let us rephrase the theorem given in the introduction of [111]:

Theorem 1.9. (The QR dressing chain integrability). The Hamiltonian (1.70)

generates an integr able ﬂow (1.71) that interpolates the QR dressing chain at

integer t.

The statement ab out asymptotic values of the oﬀ-diagonal part of the matrix

M reads

Theorem 1.10. (Moser Toda chain theorem). The matrix elements b

(t) go

to zero at both inﬁnities t →±∞.

This theorem could be applied directly to many problems of diﬀerence ap-

proximations of the Schr¨odinger equation [202].

The QR algorithm deals with invertible matrices only, but the question o f

integrability of the ﬂow (1.71) with

B(M )=(M

)

− M

where M

is strictly an upper part of M, is solved p ositively for the sym-

metric initial M

. Adler [16] and Kostant [250] proved that the Hamiltonian

20 1 Mathematical preliminaries

(M) = (trM

)/2 yields the equations of motion (1.71) on the symplectic

manifold and Deift et al. [110] found expressions for conservation laws as the

eigenvalues of the problems:



= λ

,k=0,...,[n/2],r=1,...,n− 2k,

where



is t he result of deleting the ﬁrst k rows and the last k columns of

Further generalization was achieved by Deift et al. [111] in the form of the

integrability theorem for a generic matrix M by means of the Lax represen-

tation with

B(M )=[(M

)

]

− (M

)

The additional (to the symmetric case) (n −1)

/4 integrals of motion J

are

extracted from the invariant spectral curve by means of the identity transfor-

mation

det[(1 − h)M + hM − z]=



r,k

[h(1 − h)]

M−r

The explicit expressions for the corresponding solutions of the ﬂow (1.71) are

given in terms of theta functions.

The paper [111] also contains proofs of the integrability theorems for the

other types of factorization using the Cholesky algorithm

=[((M

)

−

+(M

)

/2)

,M] (1.74)

and LU ﬂow (the LU factorization algorithm, where L is the lower triangular

matrix with unit diagonal entries and U is the upper triangular matrix)

=[((M

)

−

+(M

)

,M], (1.75)

where M

−

is the lower part of the matrix M and M

is the diagonal one, as

well as algorithms based on the factorization [189]. The possibility of blowing

up in ﬁnite time [447] should also be mentioned, as this is important for

applications.

Deift et al. [111], extending the results of the previous paper [110], used

the Lie group theory to construct orbits and symplectic structures on the basis

of the unique QL factorization

g = g

∈ O

(n, R),g

∈ L

(n, R).

1.9 Quasideterminants

This section contains a novel tool to manage block matrices (supermatrices)

which appears in the dressing theory. The history of the classical theory of

determinants and its extension related to the notion of quasideterminants

are reviewed in the excellent and profound paper [174]. Let us start with a

quotation from [174]:

1.9 Quasideterminants 21

Our experience shows that in dealing with nonco mmutative objects

one should not imitate the classical commutative mathematics, but

follow “the way it is” starting with basics.

The purpose of this section is to give a brief introduction to the theory of

quasideterminants based on the text of [174] (see also [191]).

1.9.1 Deﬁnition of quasideterminants

Let A be a matrix with numbers as entries. We write

|A|



... a

... ...

... a

... ...

... a

...a



. (1.76)

For a 2 ×2 block matrix A =(a

), i, j =1, 2, there are four quasideterminants:



= a

− a

· a

−1

· a



= a

− a

· a

−1

· a



= a

− a

· a

−1

· a



= a

− a

· a

−1

· a

We see that each of the quasideterminants |



, |



, |



,and|



is de-

ﬁned whenever the corresponding elements a

, a

,anda

are invertible.

For a generic n × n matrix (in the sense that all square submatrices of

A are invertible) there exist n

quasideterminants of A. A nongeneric matrix

may have k quasideterminants where 0 ≤ k ≤ n

Generally, the deﬁni ti on of quasideterminants is given over a ring R with

a unit element. Let A =(a

), i ∈ I, j ∈ J,beamatrixoverR.Denotebyr

the row submatrix of length n −1 obtained from the ith row of A by deleting

the element a

,andbyc

the column submatrix of height n − 1 obtained

from the jth column of A by deleting the element a

Denote by A

, i ∈ I, j ∈ J the submatrix of A obtained from A by

deleting its ith row and jth column. Then we can formulate the following.

Deﬁnition 1.11. Let I and J be ﬁnite sets with the same number of elements.

If I = {i}, J = {j},put|



= a

.If|I|, |J| > 1, the quasideterminant |A|

is deﬁned whenever the submatrix A

is invertible over R and in this case put



= a

− r

)

−1

The term “quasideterminant,” as it is used in, e.g., [191], denotes rather a

fraction of determinants.

In the context of our book, it is important to note that it is the iterated

non-Abelian DT that is written in terms of quasideterminants .

22 1 Mathematical preliminaries

1.9.2 Noncommutative Sylvester–Toda lattices

Let R be a division algebra with a derivation D : R → R.Letφ ∈ R and the

quasideterminants



(φ)=



φ Dφ ... D

n−1

Dφ D

φ ... D

... ... ... ...

n−1

φD

φ ... D

2n−2



are deﬁned and invertible. Set φ

= φ and φ

= T

(φ), n =2, 3,....

Theorem 1.12. Elements φ

, n =1, 2,... satisfy the following equations:

D[(Dφ

)φ

−1

]=φ

−1

,D[(Dφ

)φ

−1

]=φ

n+1

−1

− φ

−1

n−1

. (1.77)

If R is commutative, the determinants of the matrices used in



(φ)satisfy

a nonlinear system of diﬀerential equations. In the modern literature this

system is called the Toda latti ce [356] but in fact it was discovere d by Sylvester

[416] in 1862 and probably, should b e called the Sylvester–Toda lattice. Our

system can be viewed a s a noncommutative generalization of the Sylvester–

Toda lattice. Theorem 1.12 appeared in [177, 178] and was generalized in

[372]. The following theorem is a noncommutative analog of the famous Hirota

identities.

Theorem 1.13. For n ≥ 2

n+1

(φ)=T

φ) − T

(Dφ) · [(T

n−1

φ)

−1

− T

(φ)

−1

]

−1

· T

(Dφ).

The proof follows from the noncommutative Sylvester identity [174].

1.9.3 Noncommutative orthogonal polynomials

The results described in this subsection were obtained in [175]. Let S

,... be elements of a skew ﬁeld R and x be a commutative variable. Deﬁne

a sequence of elements P

(x) ∈ R[x], i =0, 1,... by setting P

= S

and

(x)=



... S

2n−1

n−1

... S

2n−2

n−1

... ... ... ...

... S

n−1



for n ≥ 1. The expansion of the right column implies that P

(x)isapoly-

nomial of degree n.IfR is commutative, then P

,n ≥ 0, are orthogonal

polynomials deﬁned by the moments S

, n ≥ 0. We are going to show that if

R is a free division algebra generated by S

, n ≥ 0, then polynomials P

are

indeed orthogonal with regard to a natural noncommutative R-valued product

on R[x].

1.10 The Riemann–Hilbert problem 23

Let R be a free skew ﬁeld generated by c

, n ≥ 0. Deﬁne on R a natural

anti-involution a → a

∗

by setting c

∗

= c

for all n andextendtheinvolution

to R[x] by setting (



)

∗



. Deﬁne the R-valued inner product on

R[x] by setting









i+j

∗

Theorem 1.14. For n = m we have

P

(x),P

(x) =0.

1.10 The Riemann–Hilbert problem

This section is devoted to a brief review of basic facts concerning the RH

boundary value problem which will be used in this book. More detailed expo-

sition of the RH problem can be found in [4, 167, 375, 464].

1.10.1 The Cauchy-type integral

Let us consider a class of complex functions f (ℓ)

1. Which are deﬁned for all ℓ belonging to a contour γ.Thecontourγ is

a smooth closed counterclockwise oriented curve dividing the extended

complex k-plane C (including the inﬁnite point ∞)intotwodomainsC

and C

−

2. Which obey the H¨older condition on γ:

|f(ℓ

) −f(ℓ

)|≤A|ℓ

− ℓ

,A=const, 0 <μ≤ 1. (1.78)

3. Where f (ℓ) → 0atℓ →∞.

Consider a point k in the k-plane and deﬁne a function (the Cauchy-type

integral)

φ(k)=

2πi



dℓ

f(ℓ)

ℓ − k

. (1.79)

The function φ(k)isanalyticinC, except for points on γ, and tends to zero

at k →∞. For simplicity we choose γ to be the real axis of the k-pla ne. Then

−

) corresponds to the up per (lower) half planes of C. It should be noted

that it is the H¨older condition that ensures the existence of the integral (1.79).

Indeed, we can write (1.79) as

2πi

∞



−∞

dℓ

f(ℓ)

ℓ − k

2πi

∞



−∞

dℓ

f(ℓ) − f (k)

ℓ − k

f(k)

2πi

∞



−∞

dℓ

ℓ − k

. (1.80)

The last integral on the right-hand side of (1.80) is well deﬁned, while the

ﬁrst integral exists owing to the H¨older condition.

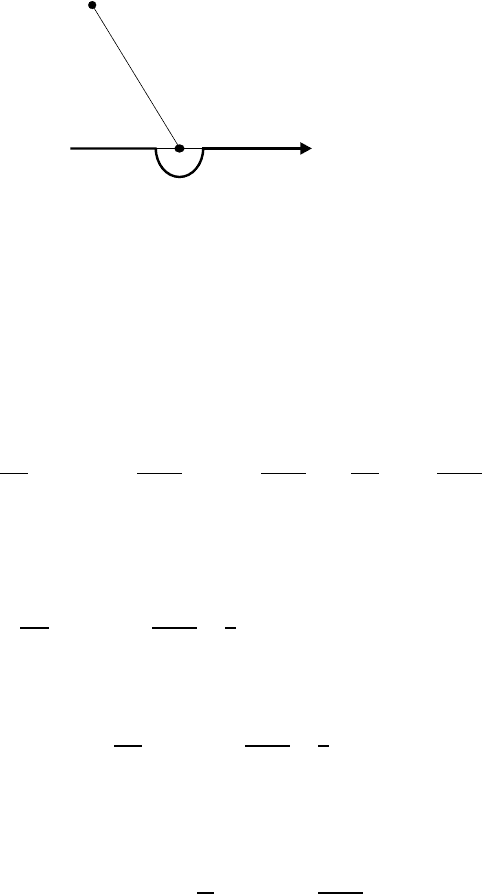
24 1 Mathematical preliminaries

Re k

Fig. 1.1. Contour of integration (bold line) when the p oint k reaches the real axis

An important question is how to deﬁne the function φ(k) for real k, i.e.,

when k belongs to the contour γ. Suppose k ∈ C

tends to the point λ on the

real axis Imk = 0, being still left in C

(Fig. 1.1). Then φ(k) tends to φ

(λ).

To evaluate φ

(λ), we deform the contour in such a way that it passes the

point λ from below. Then

(λ)=

2πi

lim

ǫ→0

⎛

⎝

λ−ǫ



−∞

dℓ

f(ℓ)

ℓ − k

∞



λ+ǫ

dℓ

f(ℓ)

ℓ − k

⎞

⎠

2πi

λ+ǫ



λ−ǫ

dℓ

f(ℓ)

ℓ −k

The ﬁrst term in the parentheses deﬁnes the principal value of the Cauchy

integral v.p.



∞

−∞

dℓf(ℓ)/(ℓ −λ) and the last integral is easily calculated after

a change ℓ − λ = ǫ exp(iθ) and integrating in θ from π to 2π. The result is

(λ)=

2πi

v.p.



∞

−∞

dℓ

f(ℓ)

ℓ − λ

f(λ), Imλ =+0. (1.81)

Similarly, we can calculate the function φ

−

(λ), which is the limit of φ(k)when

k located in C

−

tends to λ ∈ Imk = −0:

−

(λ)=

2πi

v.p.



∞

−∞

dℓ

f(ℓ)

ℓ − λ

−

f(λ). (1.82)

Hence, we derive the Sokhotsky–Plemelj formulas (1.81) and (1.82), which are

usually written as

(λ) − φ

−

(λ)=f(λ), Imλ =0, (1.83)

(λ)+φ

−

(λ)=

πi

v.p.



∞

−∞

dℓ

f(ℓ)

ℓ − λ

. (1.84)

Therefore, the Cauchy-type integral deﬁnes a sectionally continuous function

which is regular oﬀ the contour and continuous when tending to the contour

both from above and from below.

To recognize analytic properties o f φ(k), we allow the point k ∈ C

move to the point λ on the real axis, to cross the axis,and to move below the

1.10 The Riemann–Hilbert problem 25

Re k

λ-iε

Fig. 1.2. Contour of integration (bold line) when the p oint k crosses the real axis

axis to the point λ −iǫ, ǫ>0. To evaluate φ

(λ −iǫ), we deform the contour

γ as in Fig. 1.2. The calculation yields

(λ − iǫ)=

2πi



∞

−∞

dℓ

f(ℓ)

ℓ − λ +iǫ

+ f(λ − iǫ)=φ

−

(λ − iǫ)+f(λ − iǫ).z

Note that the last term does not contain the factor 1/2 b ecause the contour

encloses the point λ − iǫ almost entirely. We see that φ

(λ − iǫ)doesnot

coincide with φ

−

(λ − iǫ). Therefore, the Cauchy-type integral deﬁnes two

diﬀerent analytic functions: φ

(k), k ∈ C

and φ

−

(k), k ∈ C

−

. Accordingly,

we can write

(k)=

2πi



∞

−∞

dℓ

f(ℓ)

ℓ − k

,k∈ C

(k)=

2πi



∞

−∞

dℓ

f(ℓ)

ℓ − k

f(k), Imk =+0, (1.85)

(k)=

2πi



∞

−∞

dℓ

f(ℓ)

ℓ − k

+ f(k),k∈ C

−

Several conclusions follow from (1.85). First, φ

(k) can be analytically con-

tinued to C

−

if f(k) allows such a continuation. Second, the function φ

(k),

bein g regular in C

, acquires sin gularities in C

−

, otherwise it will be con-

stant in entire C as a regular analytic function everywhere, in accordance

with the Liouville theorem. Third, if we know a jump ∆(k)=φ

(k) −φ

−

(k)

of analytic functions φ

across the real axis Imk = 0, we can restore φ

(k)=(P

∆)(k), where projectors P

act as follows:

∆)(k)=

2πi

∞



−∞

dℓ

ℓ − (k ± i0)

∆(ℓ). (1.86)

26 1 Mathematical preliminaries

If φ

tend to some limits as |k|→∞, these limits should be added to the

integral (1.86).

1.10.2 Scalar RH problem

The scalar RH problem can be formulated as a problem of analytic factoriza-

tion of a scalar function g(k) given on a contour γ,

−

(k)φ

(k)=g(k),k∈ γ, (1.87)

in a product of functions φ

(k)analyticinC

. A solution of this problem

is not unique: functions

= φ

and

−

,whenr

(k) is a rational

function with all zeros being in C

and all poles being in C

−

,aresolutions

of (1.87) as well. To ﬁx the solution, we shall pose a normalization condition.

The condition φ

−

(∞) = 1 is called the canonical normalization.

Now we deﬁne the index of the RH problem:

ind

{g(k)} =

2πi



d{ln g(k)}.

The index measures a change of the phase of g(k)overthecontourγ.For

analytic functions the index gives the diﬀerence between the number of zeros

and poles of this function (accounting for their multiplicities) in the domain

bounded by the contour. If the index is zero, both functions φ

(k)havethe

same number of zeros in their domains of analyticity.

The scalar RH problem with zero index can be easily solved. Let k

and

, j =1,...,N be simple zeros of φ

(k)andφ

−

(k), respectively. First we

regularize these functions. This means that the functions

(0)

(k)=φ

(k)



j=1

k −

k − k

,φ

(0)

−

(k)=φ

−

(k)



j=1

k − k

k −

(1.88)

solve the same RH problem and obey the same normalization condition

as φ

(k) but have no zeros. The regularized RH problem subjected to a

given normalization condition has a unique solution. Indeed, for the functions

(k)=±ln φ

(0)

(k) equation (1.87) is written as

(k) − p

−

(k)=lng(k),k∈ γ.

Hence, we have two holomorphic functions in C

which are both zero at

inﬁnity and have the jump ln g(k) across the contour γ. Using the Sokho tsky–

Plemelj formula (1.83) and assuming the H¨older condition for ln g(k), we get

the solution

p(k)=

2πi



dℓ

ℓ − k

ln g(ℓ).

Accordingly,

(0)

(k)=exp



±1

2πi



dℓ

ℓ − k

ln g(ℓ)



,k∈ C

1.10 The Riemann–Hilbert problem 27

Therefore, the general solution to the scalar RH problem has the form

(k)=



j=1



k − k

k −



±1

exp



±1

2πi



dℓ

ℓ − k

ln g(ℓ)



,k∈ C

. (1.89)

1.10.3 Matrix RH problem

Consider the problem of analytic factorization of a matrix function G(k)

givenonacontourγ such that detG(k) =0,G(∞)=11if∞∈γ,and

ind

{detG(k)} = 0, in a product of two analytic functions Φ

(k)andΦ

−1

−

(k)

in C

and C

−

, respectively:

−1

−

(k)Φ

(k)=G(k),k∈ γ, (1.90)

with the normalization condition Φ(∞)=11 (i.e., one or both of Φ

obey this

condition). The zero index condit ion ensures that detΦ

(k) and detΦ

−1

−

(k)

have an equal number of zeros in C

and C

−

. A regularization of the matrix

RH problem is performed by some matrix functions rational in k.Theregu-

larized matrix RH problem has a unique solution similar to the scalar case.

The signiﬁcant diﬀerence, however, lies in the fact that the matrix case does

not allow an explicit general solution. The investigation of the solvability of

the regularized matrix RH problem can be reduced to that of some matrix

linear integral equation of the Fredholm type. Indeed, let Φ

(0)

(k)bematrix

functions analytic in C

that determine the regularized RH problem:

(0)−1

−

(0)

= G(k). (1.91)

Then the Sokhotsky–Plemelj formula (1.83) can be applied to Ψ

= Φ

(0)

−11,

giving

(k)=

±1

2πi



dℓ

ℓ − k

(ℓ). (1.92)

In terms of Ψ

the problem (1.91) is written as

(k)=Ψ

−

(k)G(k)+G(k) − 11,k∈ γ. (1.93)

Then we obtain from (1.92) and (1.93) the following equation for Ψ

−

(k)for

k ∈ γ:

−

(k)=

2πi



dℓΨ

−

(ℓ)K(ℓ, k)+H(k). (1.94)

The kernel K(ℓ, k) and inhomogeneous term H(k)havetheforms

K(ℓ, k)=

G(ℓ)G

−1

(k) − 11

ℓ − k

(1.95)

28 1 Mathematical preliminaries

and

H(k)=



−1

(k) − 11



2πi



dℓ

ℓ − k

[G(k) − 11] G

−1

(k).

Note the kernel K(ℓ, k) (1.95) is regular for ℓ = k; hence, the integral equation

(1.94) is of the Fredholm type. Gohberg and Krein [188] have formulated

the suﬃcient condition for the solvability of the matrix RH problem. Let us

introduce “real” and “imaginary” parts of the matrix G,

(k)=



G(k)+G

†

(k)



(k)=



G(k) − G

†

(k)



where G

†

stands for the Hermitian conjugation. Then the regularized matrix

RH problem has a solution if the real or the imaginary part of G(k) is positive

(or negative) deﬁnite. The deﬁniteness of G means that x

†

Gx is real and sign-

deﬁnite for all nonzero vectors x. Our choice of the normalization of the RH

problem is compatible with positive deﬁniteness. In applications to the soliton

theory we will encounter only the solvable matrix RH problems.

1.11

∂ Problem

The analytic function f(x, y)=u(x, y)+iv(x, y) deﬁned on the extended

complex plane (the Riemann sphere) C with the coordinates x and y obeys

the Cauchy–Riemann condition

= v

= −v

. (1.96)

In the complex coordinates z = x +iy and ¯z = x −iy equation (1.96) takes a

compact form

∂f(z, ¯z)=0,

where

∂ ≡ ∂

¯z

=(1/2)(∂

+i∂

). The Cauchy–Riemann operator

∂ measures

the “departure from analyticit y” for the function f (z, ¯z)andtheequation

∂f(z, ¯z)=g(z, ¯z) (1.97)

is referred to as the

∂ problem. The Cauchy formula (1.79) for analytic func-

tions is generalized to the case o f nonanalytic functions which satisfy (1.97)

f(z, ¯z)=

2πi



dζ

ζ − z

f(ζ,

ζ)+

2πi



dζ ∧ d

ζ − z

g(ζ,

ζ). (1.98)

Here f (z, ¯z) is any function which has smooth derivatives with respect to

both z and ¯z in some domain D in the complex plane and is continuous in

the closed domain D∪γ with a counterclockwise-oriented boundary γ.The

exterior product dz ∧ d¯z is skew-symmetric, dz ∧ d¯z = −d¯z ∧ dz,andcan

be written as dz ∧ d¯z = −2idxdy. If the domain D is the entire complex