Дипломный проект - Элективный курс. Симметрические многочлены в профильном обучении школьников
Подождите немного. Документ загружается.

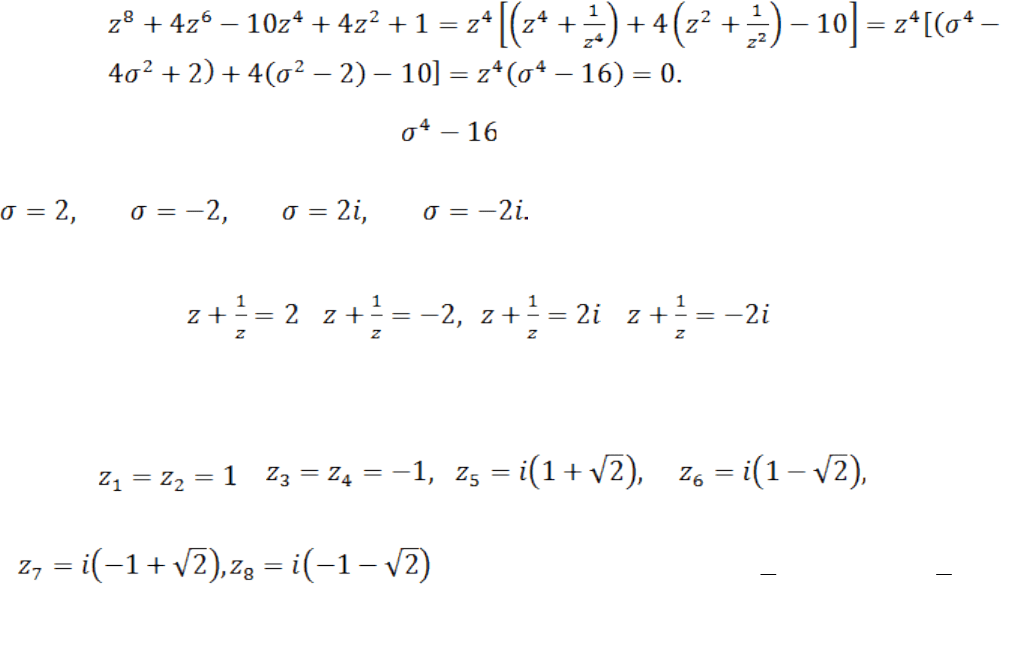
c) Решение. Имеем
Получаем двучленное уравнение =0. Его корни:
Для нахождения корней первоначального уравнения имеем четыре уравнения:
, , .
Решая их находим восемь корней первоначального уравнения:
,
,
iz
2
,
iz
3
,
2
4
z
,
2
1
5
z
,
2
6
z
,
2
1
7
z
,
1
98
zz
,
1
1110
zz
.
102
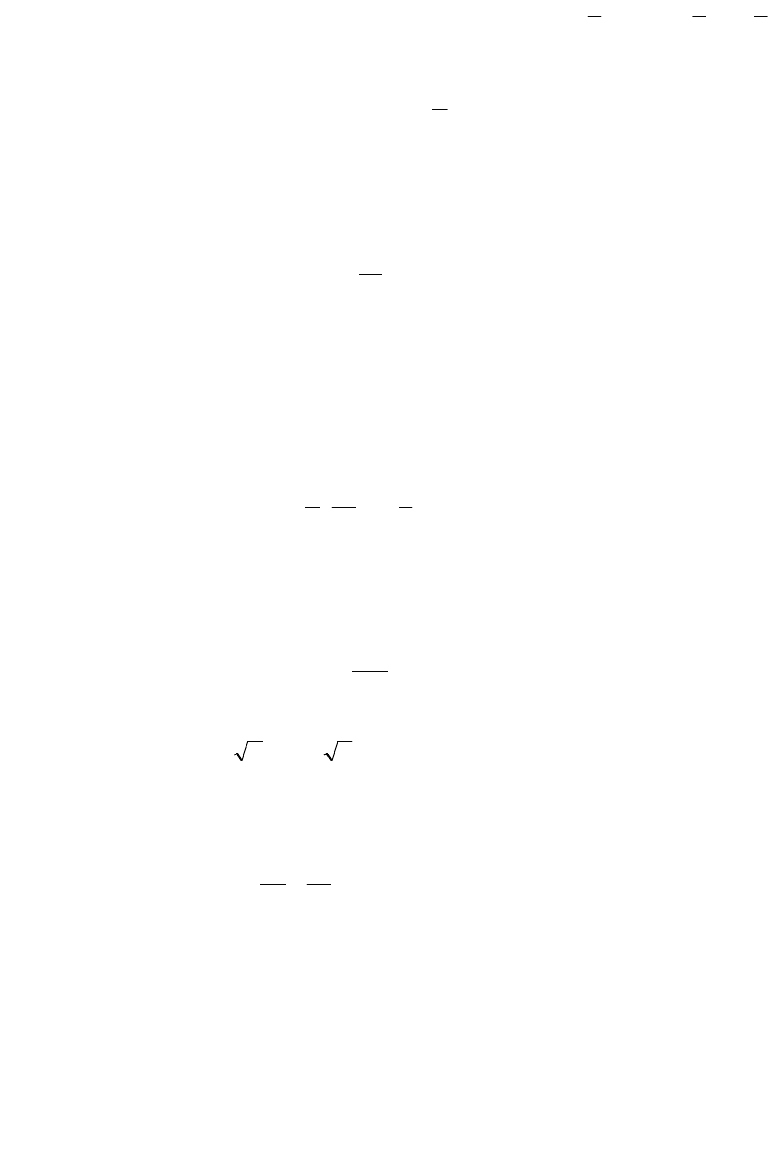
Приложение 10
Задание 6. Решение. Для доказательства введем элементарные симметрические
многочлены
ba
1
и
ab
2
, тогда
zzbas
2
1
2
1
4
1
22
2
1
2
1
2
12
2
1
22
2
.
Так как
0z
, а по условию задачи
c
1
, то
2
2
2
1
cs
, т.е.
2
2
22
c
ba
Применяя к полученному неравенству тоже рассуждения находим, что
42
2
44
8
1
)
2
(
2
1
с
c
ba
.
Аналогично находим, что
128
8
88
c
ba
.
Задание 7. Решение. Положим
ua
,
vb
. Тогда доказываемое неравенство
примет вид
vu
u
v
v
u
22
или
)(
33
vuuvvu
. Мы должны доказать справедливость этого справедливость
этого неравенства при
0,0 vu
. Имеем:
).4(43)(
2
2
1121
3
12121
3
1
33
vuuvvu
Последнее выражение в самом деле не отрицательно так как
0
1
,
04
2
2
1
(по теореме см. выше).
103
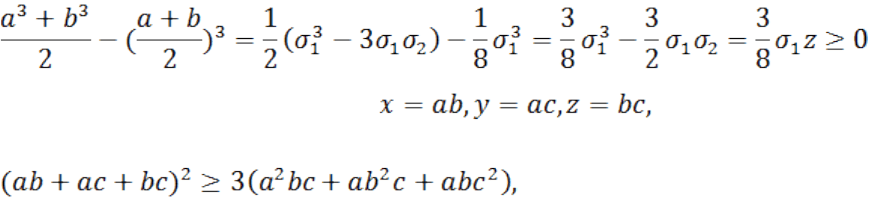
Задание 8. Решение. Мы имеем:
Задание 9. Решение. Полагая здесь получаем:
а это и есть доказываемое неравенство.
104
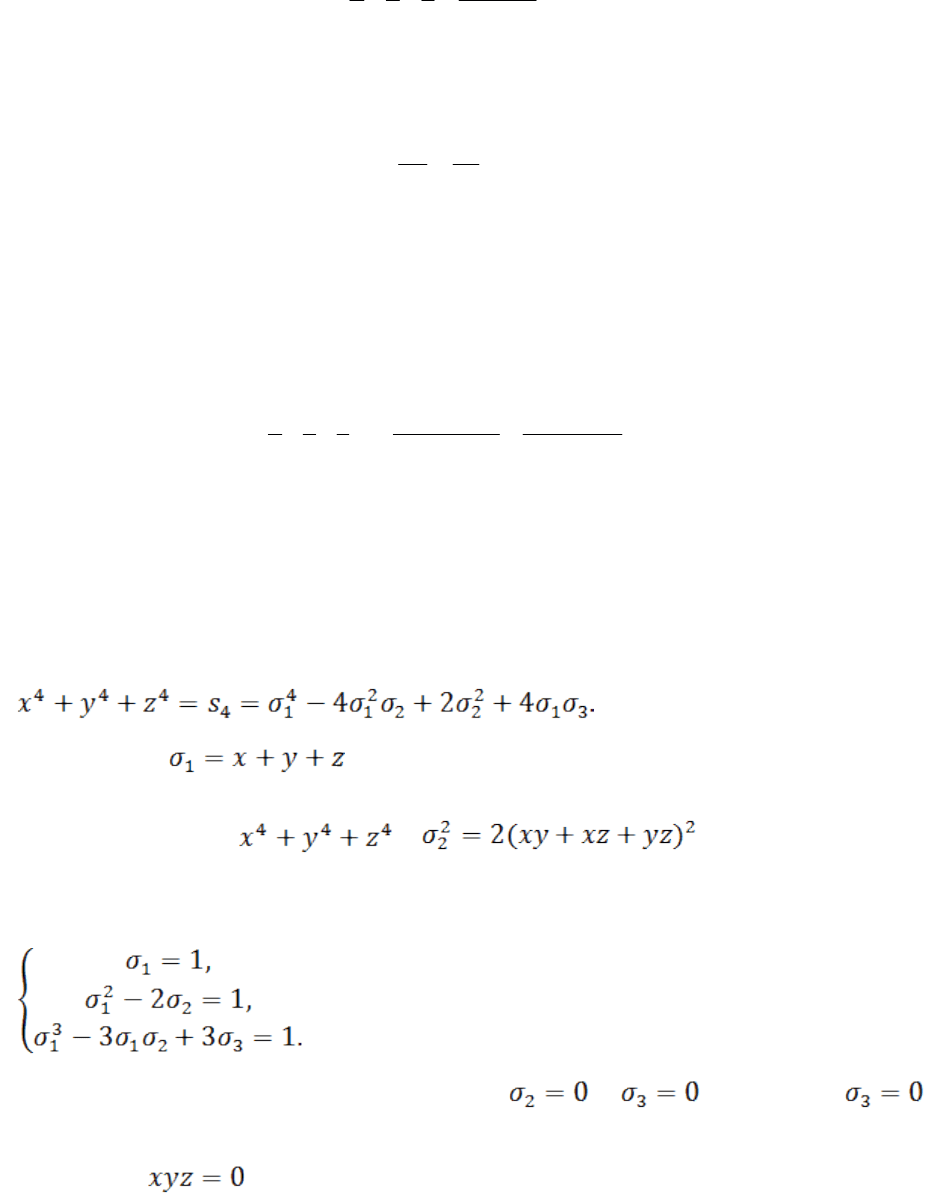
Приложение 11
Задание 10. Решение. Равенство
cbacba
1111
Можно записать в виде
,
1
13
2
т.е
0
321
, или
.0)( cbcaba
Таким образом хотя бы одно из
выражений
ba
,
ca
,
cb
равно нулю, т.е. имеет место хотя бы одно из
равенств
ba
,
ca
,
cb
. Но в таком случае равенства
.
)(
11111
nnnn
n
cbacba
cba
При нечетном n очевидны.
Задание 11.Решение. Выразим
По условию =0, и поэтому
=2 .
Задание 12. Решение. Условие задачи записывается в виде
Из этой системы равенств находим, что и . Равенство
и означает, что .
105

Приложение 12.
Теорема 3. Всякий возвратный многочлен
kk
kk
azazazazf
212
12
1
2
0
...)(
четной степени 2k представляется в виде f(z)=
)(
hz
k
, где
z
z
1
и
)(
h
-
некоторый многочлен степени k от
.
Всякий возвратный многочлен f(z) нечетной степени делится на z+1, причем
частное представляет собой возвратный многочлен четной степени.
Доказательство. 1) Рассмотрим сначала многочлен
)(zf
четной степени 2k.
Вынося в этом многочлене за скобки
k
z
, получим:
),
11
...()(
2
1
12
1
10
k
k
k
k
kkk
z
a
z
azazazzf
или принимая во внимание равенство
,
20 k
aa
,...,
121
k
aa
)....)
1
()
1
(()(
1
1
10 k
k
k
k
kk
a
z
za
z
zazzf
Докажем, что двучлены
,
1
k
k
z
z
,...
1
1
1
k
k
z
z
можно выразить через
z
z
1
.
Положим
,zx
z
y
1
, то степенная сумма
kk
k
yxs
превратится в выражение
,
1
k
k
z
z
элементарный симметрический многочлен
yx
1
- в
z
z
1
, а
элементарный симметрический многочлен
xy
2
примет значение 1. Поэтому,
подставляя в выражение степенной суммы
k
s
через
1
и
2
значения
,
1
1
z
z
1
2
, мы получим искомое выражение двучлена
k
k
z
z
1
через
.
Практически для этого удобно использовать формулы из таб. 1 Приложения 1.
Пологая в этих формулах
,
1
1
2
, получаем:
106

,2
1
2
2
2
z
z
,3
1
3
3
3
z
z
,24
1
24
4
4
z
z
………………………………………………………
2)Рассмотрим теперь случай возвратного многочлена нечетной степени 2k+1:
....)(
122
2
1
12
0
kk
kk
azazazazf
Так как этот многочлен является возвратным, т.е. выполнены равенства
,
120
k
aa
,
21 k
aa
,
122
k
aa
…,
то его можно записать в следующем виде:
)(...)()()1()(
1212
2
2
1
12
0
kk
k
kkk
zzazzazzazazf
).1(...)1()1()1(
322
2
12
1
12
0
zzazzazzaza
k
k
kkk
В каждом двучлене, стоящем в скобках, можно выделить множитель z+1,
воспользовавшись следующим хорошо известным равенством:
).1...)(1(1
22212212
zzzzzzz
mmmm
Мы получим:
),1...)(1()1(
222122
0
12
0
zzzzzzaza
kkkk
),...)(1()1...)(1()1(
22212
1
3222
1
12
1
zzzzzazzzzzazza
kkkkk
……………………………………………………………………………….
.)1()1(
k
k
k
k
zzazza
Складывая полученные выражения почленно и вынося в правой части
множитель z+1 мы получим:
),()1()( zgzzf
107

где
)(zg
- многочлен, являющийся суммой следующих многочленов:
),1...(
222122
0
zzzzza
kkk
),...(
22212
1
zzzza
kk
………………………….
.
k
k
za
Непосредственно видно, что во всех этих многочленах коэффициенты,
равноудаленные от концов, совпадают, и потому их сумма
)(zg
является
возвратным многочленом (четной степени 2k). Теорема доказана.
108
