Дехтярь М.И. Конечные автоматы (Лекции по дискретной математике)
Подождите немного. Документ загружается.


S
{0, 1}
3
S = {(x
1
(1), x
2
(1), y(1))(x
1
(2), x
2
(2), y(2)) . . . (x
1
(n), x
2
(n), y(n)) | y = y(n) . . . y(2)y(1)
n x
1
= x
1
(n) . . . x
1
(2)x
1
(1) x
2
=
x
2
(n) . . . x
2
(2)x
2
(1)}.
r
M
r L
M
= L
r
M r
r Σ ∅ ε
+, ◦,
∗
r
∅ ε a ∈ Σ
q
0
q
1
q
0
q
1
-
ε
q
0
q
1
-
a
∅ {ε} {a}
≤ k
r
k+1 (r
1
+
r
2
), (r
1
r
2
) (r
1
)
∗
M
1
=< Σ, Q
1
, q
1
0
, {q
1
f
}, Φ
1
> M
2
=< Σ, Q
2
, q
2
0
, {q
2
f
}, Φ
2
>
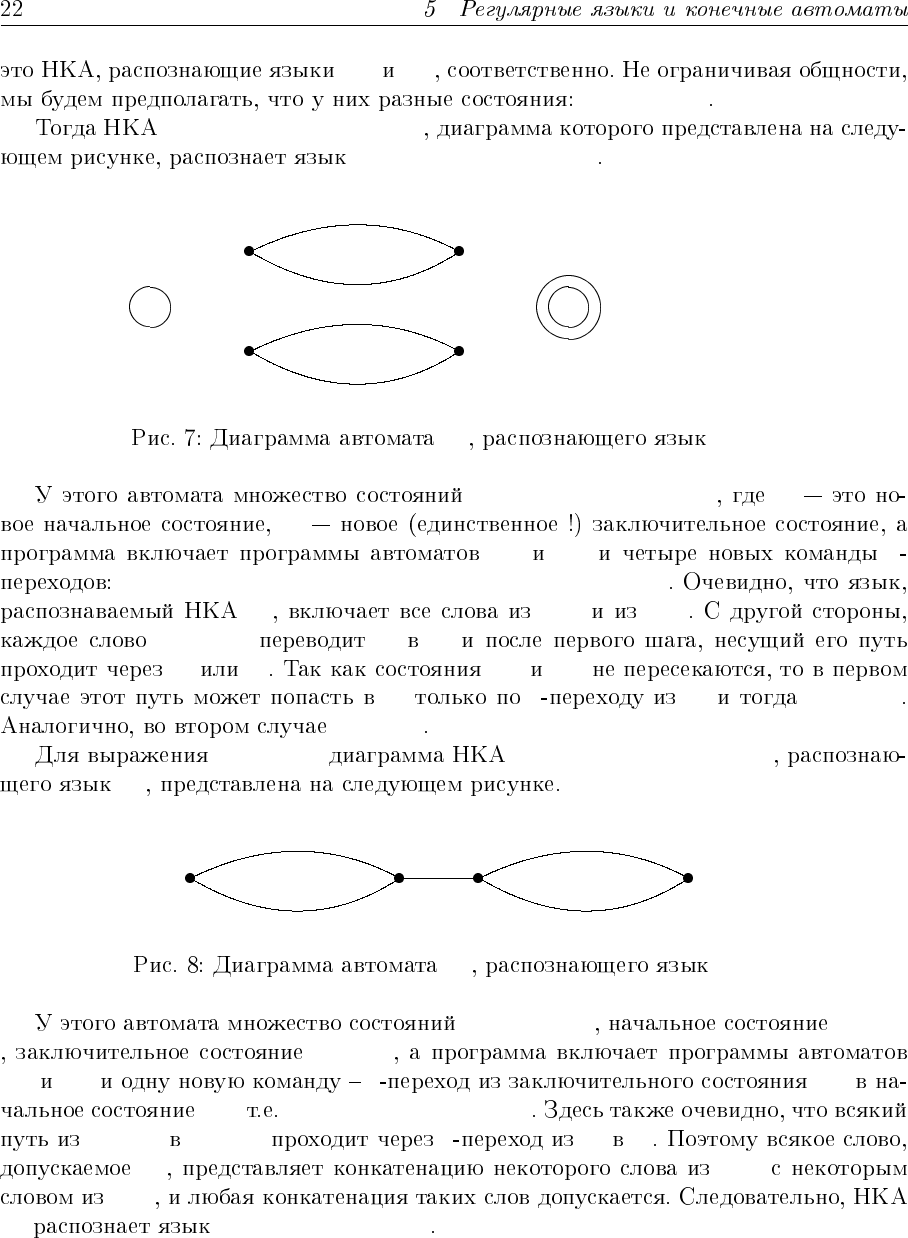
L
r
1
L
r
2
Q
1
∩ Q
2
= ∅
M =< Σ, Q, q
0
, {q
f
}, Φ >
L
r
= L
r
1
+r
2
= L
r
1
∪ L
r
2
q
1
0
q
2
0
q
1
f
q
2
f
ε
ε
ε
ε
q
0
q
f
3
Q
Q
Q
Qs
3
Q
Q
Q
Qs
M
1
M
2
M L
r
1
+r
2
Q = Q
1
∪ Q
2
∪ {q
0
, q
f
} q
0
q
f
M
1
M
2
ε
Φ = Φ
1
∪ Φ
2
∪ {q
0
→ q
1
0
, q
0
→ q
2
0
, q
1
f
→ q
f
, q
2
f
→ q
f
}
M L
M
1
L
M
2
w ∈ L
M
q
0
q
f
q
1
0
q
2
0
M
1
M
2
q
f
ε q
1
f
w ∈ L
M
1
w ∈ L
M
2
r = r
1
◦ r
2
M =< Σ, Q, q
0
, {q
f
}, Φ >
L
r
q
0
= q
1
0
q
1
f
q
2
0
q
2
f
= q
f
ε
-
M
1
M
2
M L
r
1
◦r
2
Q = Q
1
∪ Q
2
q
0
= q
1
0
q
f
= q
2
f
M
1
M
2
ε M
1
M
2
, Φ = Φ
1
∪Φ
2
∪{q
1
f
→ q
2
0
}
q
0
= q
1
0
q
f
= q
2
f
ε q
1
f
q
2
0
M L
M
1
L
M
2
M L
r
= L
r
1
◦r
2
= L
r
1
L
r
2

r = r
∗
1
M =< Σ, Q, q
0
, {q
f
}, Φ >
L
r
= L
r
∗
1
= L
∗
M
1
*
ε
ε
q
0
-
q
1
0
q
1
f
q
f
-
ε ε
M
1
M L
r
∗
1
Q = Q
1
∪ {q
0
, q
f
} q
0
q
f
M
1
ε
Φ = Φ
1
∪ {q
0
→ q
1
0
, q
0
→ q
f
, q
1
f
→ q
1
0
, q
1
f
→ q
f
} ε ∈ L
M
w w ∈ L
r
∗
1
⇔ k ≥ 1 w
k w = w
1
w
2
. . . w
k
w
i
∈ L
M
1
i = 1, . . . , k
w
i
q
1
0
q
1
f
w M q
0
ε
−→ q
1
0
w
1
−→ q
1
f
ε
−→ q
1
0
w
2
−→ q
1
f
. . . q
1
0
w
k
−→ q
1
f
ε
−→ q
f
w ∈ L
M
q
0
q
f
ε
q
0
q
1
0
q
1
0
q
1
f
q
1
f
q
1
0
ε q
1
f
ε q
f
.
w ∈ L
∗
M
1
.
2
M
r
r
a
1
a
2
. . . a
n
a
i
∈ Σ (i = 1, 2, . . . , n)
(n + 1) q
i
(i = 0, 1, 2, . . . , n)
q
i−1
a
i
→ q
i
ε
M
1
M
2
M
1
M
2
M
1
M
2
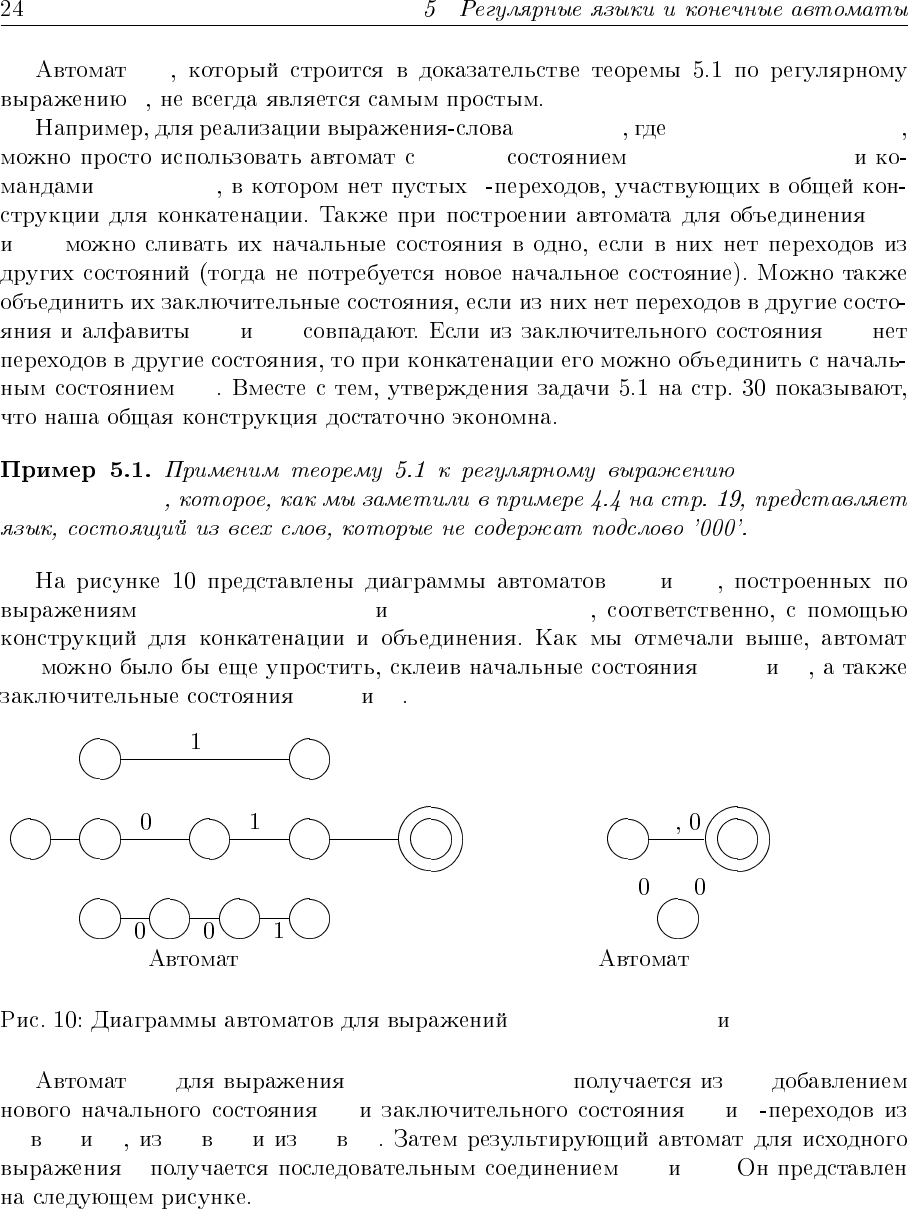
r = (1 + 01 +
001)
∗
(ε+0+00)
M
1
M
2
r
1
= (1 + 01 + 001) r
2
= (ε + 0 + 00)
M
1
q
2
, p
1
s
1
q
3
, p
3
s
4
⇒ q
1
ε
-
@
@
@R
ε
ε
q
2
-
p
1
-
s
1
-
p
2
-
s
2
-
s
3
-
q
3
@
@
@
@R
ε
p
3
-
ε
s
4
ε
q
4
⇒ q
6
-
ε
@
@
@R
q
7
q
8
M
1
M
2
r
1
= (1 + 01 + 001) r
2
= (ε + 0 + 00)
M
3
r
∗
1
= (1 + 01 + 001)
∗
M
1
q
0
q
5
ε
q
0
q
1
q
5
q
4
q
5
q
5
q
1
r M
3
M
2
.

⇒ q
0
-
ε
1
ε
q
1
ε
ε
-
@
@
@R
ε
ε
q
2
-
p
1
-
s
1
-
p
2
-
s
2
-
s
3
-
q
3
@
@
@
@R
ε
p
3
-
ε
s
4
ε
q
4
-
ε
q
5
-
ε
q
6
-
ε
@
@
@R
q
7
q
8
M L
r
L Σ
¯
L = {w | w ∈ Σ
∗
w /∈ L}
Σ
∗
Σ L = Σ
∗
\ L
Σ ∆ φ
: Σ
∗
→
∆
∗
φ(ε) = ε;
w
1
w
2
Σ φ(w
1
w
2
) =
φ(w
1
)φ(w
2
)
Σ w = w
1
w
2
. . . w
n
w
i
∈
Σ (1 ≤ i ≤ n) φ(w) = φ(w
1
)φ(w
2
) . . . φ(w
n
)
Σ = {a, b, c} ∆ = {0, 1} φ
Σ φ(a) = 00, φ(b) = ε, φ(c) = 101

φ(aca) = 0010100, φ(abcb) = 00101, φ(bbb) = ε
φ : Σ
∗
→ ∆
∗
L
Σ φ(L) L φ
φ(L) = {φ(w) | w ∈ L} L
L ∆ φ
φ
−1
(L) = {w ∈ Σ
∗
| φ(w) ∈ L}
Σ φ L
φ : Σ
∗
→ ∆
∗
L
Σ φ(L)
A =< Σ, Q, q
0
, F, Φ > L
M =< ∆, Q
M
, q
M
0
, F
M
, Φ
M
> φ(L)
q q
0
a ∈ Σ
A q q
0
φ(a) M
Σ = {a
1
, . . . , a
m
} Q = {q
0
, q
1
, . . . , q
n
} φ(a
i
) = d
i
1
d
i
2
. . . d
i
k
i
, d
i
l
∈ ∆ (1 ≤ l ≤
k
i
) φ(a
i
) 6= ε a
i
M
i
{d
i
1
d
i
2
. . . d
i
k
i
} (k
i
+ 1) p
i
0
, p
i
1
, . . . , p
i
k
i
p
l−1
d
i
l
→
p
l
(1 ≤ l ≤ k
i
) φ(a
i
) = ε M
i
ε
q
j
a
i
→ q
r
M q
j
q
r
M
i
p
i
0
, p
i
1
, . . . , p
i
k
i
j q
j
M
i
Q
M
= Q ∪ {p
ji
l
| 0 ≤ j ≤ n, 1 ≤ i ≤
m, 0 ≤ l ≤ k
i
} p
ji
l
l q
j
a
i
Φ
M
M A
q
j
a
i
→ q
r
Φ Φ
M
q
j
→ p
ji
0
,
p
ji
0
d
i
1
→ p
ji
1
,
• • •
p
ji
k
i
−1
d
i
k
i
→ p
ji
k
i
,
p
ji
k
i
→ q
r
q
j
M
p
ji
0
j M
i
φ(a
i
)
q
r
M q
M
0
= q
0
F
M
= F
φ(L) = φ(L
A
) = L
M
φ(L) ⊆ L
M
. ε ∈ L q
0
∈ F
q
0
∈ F
M
φ(ε) = ε ∈ L
M
.

w = w
1
w
2
. . . w
k
∈ L, w
s
∈ Σ A q
0
q
0
∈ F w
q
0
= q
j
0
, q
j
1
, . . . q
j
k
= q
0
1 ≤ x ≤ k Φ
q
j
x−1
w
x
→ q
j
x
Φ
M
M
q
j
x−1
q
j
x
φ(w
x
)
q
0
q
0
∈ F
M
φ(w) φ(w) ∈ L
M
L
M
⊆ φ(L). u ∈ ∆
∗
L
M
w ∈ L u = φ(w) M q
0
q
0
∈ F
M
u Q
q
0
= q
j
0
, q
j
1
, . . . q
j
k
= q
0
u k
u = u
1
u
2
. . . u
k
u
x
M q
j
x−1
q
j
x
1 ≤ x ≤ k
u
x
w
x
∈ Σ u
x
= φ(w
x
) Φ
q
j
x−1
w
x
→ q
j
x
q
j
x−1
M
ε p
j
x−1
i
0
u
x
q
j
x
p
j
x−1
i
l
(l = 1, . . . , k
i
) ε p
j
x
i
k
i
q
j
x
M u
x
= φ(a
i
) Φ q
j
x−1
w
x
→ q
j
x
w
x
= a
i
u
x
= φ(w
x
) u = φ(w
1
)φ(w
2
) . . . φ(w
k
) = φ(w),
w = w
1
w
2
. . . w
k
∈ Σ
∗
w
x
A q
j
x−1
q
j
x
A q
0
q
0
∈ F
w w ∈ L
2
Σ ∆ φ
L = {w | w }
A L
M
a
φ(a) = 00 M
b
φ(b) = ε M
c
φ(c) = 101
⇒ q
0
a
-
b, c
?
a
q
1
?
b, c
M
a
:
0 0
p
1
0
-
p
1
1
-
p
1
2
M
b
:
p
1
0
p
1
1
-
ε
M
c
:
1 0
p
3
0
-
p
3
1
-
p
3
2
-
1
p
3
3
A L M
a
, M
b
M
c
A a M
a
b M
b
c M
c
M φ(L)
ε q
0
q
1
ε M
b

1 0
p
03
0
-
p
03
1
-
p
03
2
-
1
p
03
3
1 0
p
13
0
-
p
13
1
-
p
13
2
-
1
p
13
3
0 0
p
01
0
-
p
01
1
-
p
01
2
0 0
p
11
2
p
11
1
p
11
0
q
0
⇒
εε ε
ε
ε
?
@
@
@
@
@
@I
+
1 P
P
P
P
Pq
ε
ε
εεε
?
q
1
P
P
P
P
P
P
P
P
P
P
P
Pi
M φ(L)
M
ε
M
i
A
p
0
0
p
01
0
q
0
p
01
2
p
13
3
q
1
∆ ⊂ Σ L Σ
∆
P ROJ
∆
(L) = {w | w v ∈ L
∆}.
π : Σ
∗
→ ∆
∗
π(a) = a a ∈ ∆
π(a) = ε a /∈ ∆ L Σ
P ROJ
∆
(L) = π(L)
∆ Σ ∆ ⊂ Σ
L Σ P ROJ
∆
(L)
M PROJ
∆
(L) A
L A
σ \ ∆ ε
φ : Σ
∗
→ ∆
∗
L
∆ φ
−1
(L)

A =< ∆, Q, q
0
, F, Φ > L
Σ = {a
1
, . . . , a
m
} Q = {q
0
, q
1
, . . . , q
n
} φ(a
i
) = d
i
1
d
i
2
. . . d
i
k
i
, d
i
l
∈ ∆ (1 ≤ l ≤ k
i
)
φ(a
i
) 6= ε
M =< Σ, Q, q
0
, F, Φ
M
>
φ
−1
(L)
q q
0
a ∈ Σ M A φ(a) 6= ε q q
0
a ∈ Σ φ(a) = ε M a
a φ
−1
(L)
q
j
∈ Q a
i
∈ Σ Φ
M
(q
j
, a
i
) = q
r
,
φ(a
i
) 6= ε A (q, φ(a)) `
∗
A
q
r
φ(a) = ε Φ
M
(q
j
, a
i
) = q
j
.
A Φ
M
q
j
∈ Q a
i
∈ Σ M
L
M
= φ
−1
(L) w = a
i
1
a
i
2
. . . a
i
k
∈
L
M
M q
0
, q
i
1
q
i
2
. . . q
i
k
q
i
k
∈ F Φ
M
A
q
0
q
i
k
∈ F φ(a
i
1
)φ(a
i
2
) . . . φ(a
i
k
) = φ(w)
w ∈ φ
−1
(L)
w = a
i
1
a
i
2
. . . a
i
k
∈ φ
−1
(L) u = φ(w) = φ(a
i
1
)φ(a
i
2
) . . . φ(a
i
k
) ∈
L A u, q
0
q
0
∈ F q
i
j
φ(a
i
1
)φ(a
i
2
) . . . φ(a
i
j
) u (j = 1, 2, . . . , k).
q
i
k
= q
0
j = 1, 2, . . . , k (q
i
j−1
, φ(a
i
j
) `
∗
A
q
i
j
.
Φ
M
M j = 1, 2, . . . , k
(q
i
j−1
, a
i
j
) `
M
q
i
j
. M q
0
, q
i
1
q
i
2
. . . q
i
k
w
q
i
k
= q
0
w ∈ L
M
2
Σ ∆ φ
φ(a) = 00, φ(b) = ε, φ(c) = 101 L = {w | w
}
A L
a b
c
M
q
2
q
3
q
0
M L
M
= φ
−1
(L) = {u | u c}.

⇒ q
0
q
1
q
2
q
3
-
-
0
0
0
0
? ?
6 6
1 1 1 1
A L(A) = L
⇒
-
a, b
q
0
-
a, b
q
1
a, b
q
2
a, b
q
3
-
-
c
c
c
c
M φ
−1
(L)
M
r
r
M
r
q
f
M
r
M
r
r
|Q| ≤ 2|r|
M
M
∆ Σ ∆ ⊂ Σ L ∆
CY L
Σ
(L) = {w ∈ Σ
∗
| ∆
u ∈ L)
L CY L
Σ
(L)
L CY L
Σ
(L)
