Деева Е.М. Методические указания по решению типовых задач по дисциплине Линейная алгебра и линейное программирование
Подождите немного. Документ загружается.

11
,
...
21
....
2
...
2221
1
...
1211
=
nn
a
n
a
n
a
n
aaa
n
aaa
A
.
2
1
,
2
1
=
=
n
x
x
x
X
n
b
b
b
B
MM
Если
А
– невырожденная матрица, т. е. ее определитель
|А| ≠ 0
, то можно
определить
А
-1
.
С учетом этого имеют место матричные соотношения:
А
-1
· А· Х = А
-1
· В, Е · Х = А
-1
· В, Х = А
-1
· В
. (1.2)
Обратная матрица может быть определена на базе следующей теоремы.
Теорема о существовании обратной матрицы. Если определитель матрицы
А не равен нулю, то матрица А имеет обратную матрицу А
---1
, которая
находится по формуле
ΑΑ
∆
=
−
Α
где,
1
1
– матрица, присоединенная к матрице А.
Матрица
Α составляется из алгебраических дополнений к элементам
транспонированной матрицы:
.
...
21
....
2
...
2212
1
...
2111
=
nn
A
n
A
n
A
n
AAA
n
AAA
A
Таким образом, соотношение (1.2) лежит в основе решения системы
уравнений (1.1) методом обратной матрицы.
Рассмотрим систему m линейных уравнений с n неизвестными (при m < n
такие системы называются неопределенными):
,11
...
212111
b
n
x
n
axaxa =+++
,22
...
222121
b
n
x
n
axaxa =+++ (1.3)
…………………………………
m
b
n
x
mn
ax
m
ax
m
a =+++ ...
2211
,
или в векторной записи:
А
1
х
1
+ А
2
х
2
+ …+ А
n
х
n
= В,

12
где А
1
=
=
2
22
12
2
,
1
21
11
m
a
a
a
A
m
a
a
a
M
M
,…, А
n
=
=
m
b
b
b
B
mn
a
n
a
n
a
M
M
2
1
,
2
1
–
соответствующие вектор-столбцы.
Запишем расширенную матрицу этой системы в виде
А
1
А
2
… А
n
B
Элементарными
преобразованиями
системы (1.3) (или
матрицы
∧
A
) называются следующие преобразования:
• перестан овка любых двух уравнений;
• умножение обеих частей одного из уравнений на любое отличное от
нуля число;
• прибавление к обеим частям одного уравнения соответствующих
частей другого, умноженных на любое число, отличное от нуля;
• вычеркивание нулевой строки (уравнения с нулевыми
коэффициентами и свободным членом, равным 0).
Можно показать, что элементарные преобразования переводят данную
систему уравнений в эквивалентную систему. Две системы линейных
уравнений называются эквивалентными, или равносильными, если каждое
решение первой системы (если они существуют) является решением второй, и
наоборот. Соответствующие расширенные матрицы также называются
эквивалентными.
При практическом решении системы линейных уравнений методом
Жордана-Гаусса последовательно над строками матрицы
∧
A выполняются
элементарные преобразования так, что некоторое неизвестное исключается из
всех уравнений, кроме одного, т. е. в составе расширенной матрицы
формируется единичная матрица.
В процессе решени я могут встретиться следующие случаи.
1. Будет получена матрица
∧
A
'
, эквивалентная матрице
∧
A
, в левой части
.
.
2
1
...
21
....
2
...
2221
1
...
1211
=
∧
m
b
b
b
mn
a
m
a
m
a
n
aaa
n
aaa
A

13
некоторой ее строки стоят нули, а в правой – число, отличное от нуля, что
соответствует уравнению
0х
1
+ 0х
2
+ … + 0х
n
=
/
i
b
,
/
i
b
≠ 0.
Это признак несовместности системы (1.3), т. е. система не имеет решени й.
2. В результате преобразований получена матрица
∧
A
'
вида:
∧
A
'
= .
1...00
.....
2
0...10
1
0...01
′
′
′
n
b
b
b
В этом случае система (1.3) совместна, определенная и имеет единственное
решение:
х
1
=
....,,
22
,
1 n
b
n
xbxb
′
=
′
=
′
3. На некотором этапе получена расширенная матрица вида
∧
A
'
= .
.
2
1
...
1
1...00
.......
2
...
12
0...10
1
...
11
0...01
′
′
′
′
+
′
′
+
′
′
+
′
r
b
b
b
rn
a
rr
a
n
a
r
a
n
a
r
a
Система совместна и имеет бесчисленное множество решений. Общее
решение системы можно записать в виде:
x
1
=
n
x
n
a
r
x
r
ab
1
...
1111
′
−−
++
′
−
′
,
x
2
=
n
x
n
a
r
x
r
ab
2
...
1122
′
−−
++
′
−
′
,
……………………………….
x
r
=
....
11
n
x
rn
a
r
x
rr
a
r
b
′
−−
++
′
−
′
Придавая каждой из стоящих в правых частях равенств переменных х
r+1
,
х
r+2
, …, х
n
произвольные значения, будем полу чать частные решения системы.
Неизвестные х
1
, х
2
,…, х
r
называются базисными, или основными, они
соответствуют линейно -независимым векторам А
1
,…, А
r
.
Таким образом, любые r переменных называются базисными (основными),
если определитель матрицы коэффициентов при них отличен от нуля, а
остальны е (n – r) переменных называются свободными, или неосновными.
Базисным решением системы уравнений называется частное решение, в
котором неосновные переменные имеют нулевые значения. Каждому
разбиению на основные и неосновные переменные соответствует одно базисное
решение, а количество способов разбиения не превышает величины

14
.
)!(!
!
mnm
n
m
n
C
−
=
Если все компоненты базисного решения неотрицательны, то такое решение
называется опорным.
Пример 3. Исследовать систему уравнений методом Жордана-Гаусса
х
1
– 2х
2
+ 3х
3
– 4х
4
+ 2х
5
= 4
х
2
- х
3
+ х
4
+ 4х
5
= -3
х
1
+ 3х
2
– 3х
4
= 1
х
1
+ х
2
+ х
3
– 3х
4
+ 3х
5
= 1
Решение. Запишем расширенную матрицу системы уравнений и
последовательно преобразуем ее элементарными преобразованиями
→
−
−
−
−
−−
−
−−
→
−
−
−
−
−−
3
3
3
4
11230
21350
41110
24321
1
1
3
4
33111
03031
41110
24321
→
−
−
−
−
−
→
−
−
−−
−−
−
−
→
6
0
3
2
112100
00000
41110
102101
6
12
3
2
112100
224200
41110
102101
−
−−
−−→
6
3
8
112100
71010
210001
6
5
11
4
2
3
3
5
7
42
8
5
21
=−−
=−−
−=+
xxx
xxx
xx
.
Таким образом, система совместна, имеет бесчисленное множество
решений. Общее решение записывается в виде
х
1
= – 8 – 21х
5
,
х
2
= 3 + х
4
+ 7х
5
,
х
3
= 6 + 2х
4
+ 11х
5
.
Любое частное решение получается из общего путем придания конкретных
значений свободным переменным х
4
и х
5
. Например, (– 8; 4; 8; 1; 0) –
частное решение. Одно из базисных решений получаем при х
4
= х
5
= 0, т. е.
(– 8 ; 3; 6; 0; 0). Число базисных решений не превосходит .10
3
5
=C Перейдем
к другому базисному решению, взяв в расширенной матрице в качестве
базисных векторы А
1
, А
2
, А
4
; при этом переменные х
1
, х
2
,
х
4
будут базисными, а

15
х
3
,
х
5
– свободны ми. Переход от одного базиса к другому осуществим методом
Жордана-Гаусса, т. е. используя элементарные преобразования:
.
3
0
8
5,515,000
5,105,010
210001
3
3
8
5,515,000
71010
210001
6
3
8
112100
71010
10001
−
−
−
−−→
−
−
−−
−−→
−
−−
−−
Таким образом, полученное еще одно базисное решение: (– 8; 0; 0; – 3; 0)
и т. д. Заметим, что оба полученных базисных решения не являются опорными
решениями.
Тема 3. Линейные векторные пространства
Определение. Упорядоченная система из n действительных чисел
n
aaa ,...,
2
,
1
называется n-мерным вектором и обозначается
).,...,
2
,
1
(
n
aaaAa ==
Числа
j
a
(j = 1, 2,…, n) называются компонентами
вектора
.
Aa =
Определение. Совокупность всевозможных n-мерных векторов с
введенными в нее операциями сложения и умножения на число называется n-
мерным векторным пространством.
В матрице из m строк и n столбцов строки являются n-мерными векторами,
столбцы – m-мерными векторами и т. д.
Вектор
),...,
2
,
1
(
n
aaaa =
и вектор
),...,
2
,
1
(
n
bbbb =
равны, если совпадают
их компоненты, стоящие на одинаковых местах, т. е. если
j
b
j
a =
при j = 1,2,…,n.
Суммой векторов
ba
и
называется вектор
).,...,
22,11
(
n
b
n
abababa +++=+ Роль нуля играет нулевой вектор
).0,...,0,0(0 =
Противоположным вектору a называется вектор
);,...,
2
,
1
(
n
aaaa −−−=−
очевидно, что
.0)( =−+ aa
Разность векторов ).( baba −+=−
Произведением вектора a на число
λ
называется вектор
).,...,
2,1
(
n
aaaa
λλλλ
= Из этого определения вытекают следующие важные
свойства:

16
,)( baba
λλλ
±=±
,)( aakak
λλ
+=±
.)()(
akak
λλ
=
Следствиями этих свойств являются следующие свойства:
.00,,)1(,00 =⋅−=−=⋅
λ
aaa
Скалярным произведением двух векторов
ba и (А и В) называется действительное число, равное сумме
произведений соответствующих компонент этих векторов:
АВ =
....
2211
n
b
n
ababa +++
Например , левая часть линейного уравнения
b
n
x
n
axaxa =+++ ...
2211
может быть представлена в виде скалярного произведения векторов А · Х, где
А =
,,...,
2
,
1 n
aaa
Х =
.,...,
2
,
1 n
xxx
Вектор В называется линейной комбинацией векторов
А
1
, А
2
,…, А
n
,
если
существуют такие числа
,,...,
2
,
1
n
λλλ
при которых выполняется соотношение
В
....
2211 n
A
n
AA
λλλ
+++=
Система векторов
r
AAA ,...,
2
,
1
(r ≥ 2) называется
линейно-зависимой, если хотя бы один из векторов системы является линейной
комбинацией остальных, и линейно-независимой – в противном случае. Можно
сформулировать следующие равносильные сказанному определения.
Система векторов
r
AAA ,...,
2
,
1
– линейно-зависимая, если существуют
такие числа
r
λλλ
,...,
2
,
1
, не все равные нулю, при которых имеет место
равенство
.0...
2211
=+++
r
A
r
AA
λλλ
Если последнее соотношение возможно лишь в случае, когда все
),1(0 rj
j
==
λ
, то система векторов называется линейно-независимой.
Например , система векторов А
1
=(2, 4, 3), А
2
= (2, 3, 1), А
3
= (5, 3, 2),
А
4
= (1, 7, 3) линейно-зависима: А
1
+ 2А
2
– А
3
– А
4
= 0.
Рангом системы векторов
),
1
,...,
12
,
11
(
1
n
aaaA =
),
2
,...,
22
,
21
(
2
n
aaaA =
………………………..
mn
a
m
a
m
a
m
A
,...,
2
,
1
(=
)
называется максимальное число линейно-независимых векторов этой системы.
Ранг системы векторов равен рангу матрицы А, составленной из компонент

17
векторов этой системы, т. е. наивысшему порядку минора матрицы А,
отличного от нуля.
Пимер 4. Определить, является ли система векторов А
1
= (5, 4, 3, 2),
А
2
= (3, 3, 2, 2), А
3
= (8, 1, 3, – 4) линейно-зависимой; если она линейно-
зависима, то найти ее максимальную линейно-независимую подсистему.
Решение. Составим матрицу из компонент векторов и найдем ее ранг. Имеем
.
4318
2233
2345
−
=A
Минор второго порядка .03
33
45
≠=
Рассмотрим два минора третьего порядка, которые его окаймляют:
.0)5959(2
418
233
245
,0118118
318
233
345
=−=
−
=−=
Ранг матрицы А равен 2, поэтому система векторов является зависимой. В
матрицах, составленных из компонент любых двух векторов данной системы,
содержатся миноры второго порядка, отличные от нуля, например:
.027
18
45
,021
18
33
,03
33
45
≠−=≠−=≠=
Поэтому максимальная линейно-независимая подсистема состоит из двух
любых векторов, а третий вектор является их линейной комбинацией.
Базисом n-мерного пространства называется любая совокупность n линейно-
независимых векторов этого же пространства.
Теорема о единственном представлении вектора. Любой вектор n-
мерного пространства можно представить как линейную комбинацию векторов
базиса, притом единственным образом.
Один из базисов n–мерного векторного пространства образует система
единичных векторов
Е
1
= (1,0,…,0)
Е
2
= (0,1,…,0)
……………..
Е
n
= (0,0,…,1).

18
Компоненты любого n –мерного вектора можно считать координатами этого
вектора в единичном базисе.
Пусть заданно n-мерное линейное пространство Е
n
.
Определение. Множество Х называется выпуклым, если вместе с любыми
точками х
1
и х
2
множеству принадлежат точки (отрезок)
.10всехпри
1
)1(
2
≤≤−+
λλλ
xx
Множество на рис. 1.1, а – выпуклое, на рис. 1.1, б – невыпуклое.
Рис. 1.1
Определение. Функция
f (
X
)
, заданная на выпуклом множестве
n
EX ⊂ ,
называется выпуклой, если для любых двух точек х
1
и х
2
из Х и любого числа
10 ≤≤
λ
выполняется соотношение
[]
).
1
()1()
2
(
1
)1(
2
xfxfxxf
λλλλ
−+≤−+
Определение. Функция f (
X
), заданная на выпуклом множества
X
,
называется вогнутой, если для любых двух точек х
1
и х
2
из Х и любого числа
10 ≤≤
λ
выполняется соотношение
[]
).
1
()1()
2
(
1
)1(
2
xfxfxxf
λλλλ
−+≥−+
Если приведенные неравенства считать строгими и они выполняются при
10 <<
λ
, то функция f (
X
) – строго выпуклая (вогнутая).
Можно показать, что если
f (
X
)
– выпуклая функция, то функция
f (
X
)
–
вогнутая, и наоборот.
На рис. 1.2, а функция f (
X
) – выпуклая, на рис.1.2, б – вогнутая.
Рис. 1.2
19
Справедливы следующие утверждения относительно выпуклых множеств и
функций.
1. Пересечение выпуклых множеств есть выпуклое множество.
2. Сумма вогнутых (выпуклых) функций есть вогнутая (выпуклая) функция.
3. Если f ( X ) выпуклая функция при
0≥X
, то множество всех точек,
удовлетворяющих условиям
bXf ≤)(
,
0≥X
, выпукло (если оно не
пустое; b - постоянная).
4. Пусть f ( X ) – выпуклая (вогнутая) функция, заданная на замкнутом
выпуклом множестве
n
EX ⊂ , тогда любой локальный минимум
(максимум) f ( X ) на Х является и глобальным.
Приведем необходимое и достаточное условие выпуклости функции многих
переменных. Пусть функция f (
),...,,(
21 n
xxxX =
) имеет все частные
производные второго порядка, образующие матрицу
.
2
2
...
2
2
1
2
......
2
2
...
2
2
2
21
2
1
2
...
21
2
2
1
2
)(
∂
∂
∂∂
∂
∂∂
∂
∂∂
∂
∂
∂
∂∂
∂
∂∂
∂
∂∂
∂
∂
∂
=
n
x
f
x
n
x
f
x
n
x
f
n
xx
f
x
f
xx
f
n
xx
f
xx
f
x
f
XQ
Эта функция является выпуклой в области Х тогда и только тогда, когда
матрица Q для любой точки из этой области является неотрицательно
(положительно) определенной. Напомним, что квадратная матрица
nnji
qQ
×
= )
,
(
называется неотрицательно (положительно) определенной,
если все определители
,
21
22221
11211
,,
2221
1211
2
,
111
nn
q
n
q
n
q
n
qqq
n
qqq
n
qq
qq
q
L
L
L
K
⋅⋅⋅⋅
=∆=∆=∆
т. е. все главные миноры матрицы Q неотрицательны
(положительны).
Пример 5. Показать, что функция
()
6
2
3
1
2 −+= xxXf является выпуклой
20
при
x
1
≥ 0.
Составим матрицу из частных производных второго порядка для
() ()
.
00
0
1
12
:
=
x
XQXf
Найдем определители
∆
1
= 12х
1
, ∆
2
= 0.
Так как при
∆
1
≥ 0, ∆
2
= 0
при
x
1
≥ 0,
то функция является выпуклой.
Дадим определение глобального и локального максимумов. Функция
(
)
xf
достигает на замкнутом (т. е. включающем свою границу) множестве X
глобальный максимум в точке
*
x
, если для любой точки, принадлежащей
Х(
Xx ∈
), выполняется условие
()
≤
*
xfxf .
Функция
(
)
xf
достигает на замкнутом множестве
X
локального максимума
в точке
х
0
, если существует некоторая окрестность этой точки, для каждой
точки которой выполняется условие
()
.
0
≤ xfxf
Определения локального и глобального минимума формулируются
аналогично.
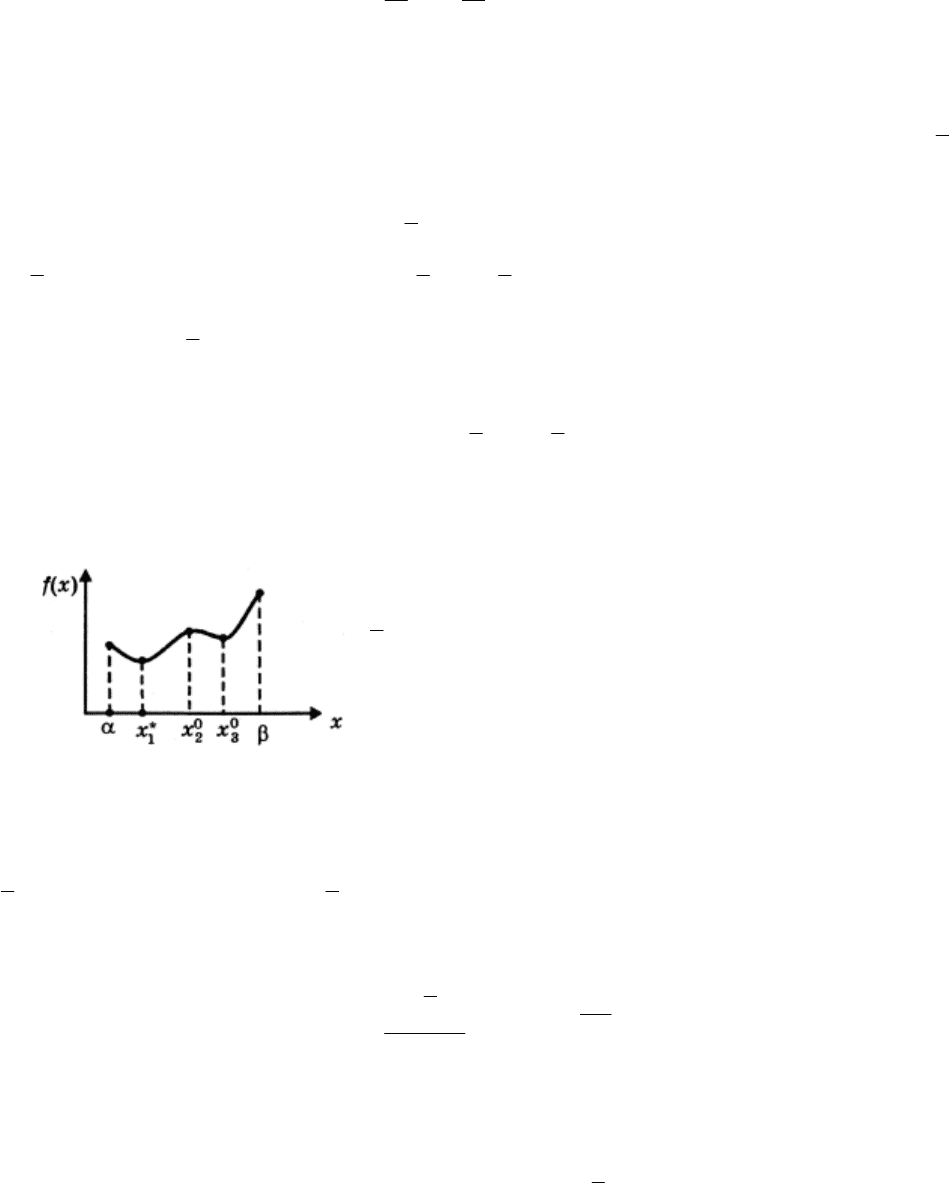
На рис. 1.3
0
3
x - точка локального минимума;
∗
1
x - глобального минимума;
0
2
, x
α
- точки
локального максимума;
β
- точка глобального
максимума.
Рис.1.3
Необходимые условия экстремума (максимума, минимума). Если в точке
Xx ∈
0
функция
),...,
2
,
1
()(
n
xxxfxf =
имеет экстремум, то частные
производные первого порядка равны нулю в этой точке:
.,1,0
)
0
(
nj
j
x
xf
==
∂
∂
Достаточные условия существования экстремума здесь не
формулируются. О самом существовании точек глобального минимума и
максимума говорит следующая теорема.
Теорема Вейерштрасса. Если функция
(
)
xf
определена и непрерывна в
ограниченной замкнутой области X, то она достигает в ней своих точных
