Данченко С.А. Решение задач по курсу Математические методы в психологии
Подождите немного. Документ загружается.

12
Задача 9. Определялось значение IQ по Векслеру, у родителей и их детей.
Результаты приведены в таблице (0 – IQ ниже среднего, 1 – IQ выше
среднего). Определить коэффициент корреляции между уровнем интеллекта
у родителей и их детей.
Дети Родители
ad
2012
=240
bc
3659
=2124
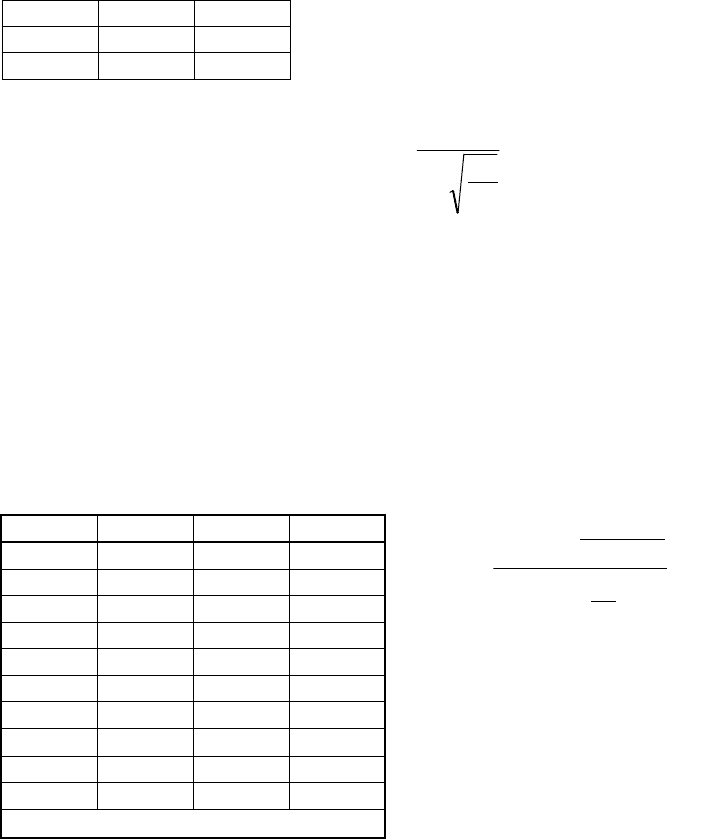
rtet=
ad
bc
1
180cos
0
=0,969447
a – 00
b – 01
c – 10
d – 11
Задание 10. На основании данных IQ родителей и их детей построить
уравнение регрессии и определить значение входящих в него параметров.
0 1
0 12 36
1 59 20
X Y XY
X
2
113 109 12317 12769
94 130 12220 8836
115 131 15065 13225
118 112 13216 13924
127 106 13462 16129
128 118 15104 16384
119 87 10353 14161
92 111 10212 8464
132 95 12540 17424
91 129 11739 8281
1129 1128 126228 129597
n
x
x
n
yx
XY
b
2
2
=-0,00963
y=bx+α
α=y-bx
α= 112.8-0.009∙112.9=113,8872
уравнение регрессии имеет вид
y=-0,00963x+113,88
13
Раздел 3. Проверка статистических гипотез.
Проверка статистической гипотезы состоит в том, чтобы определить
вероятность случайности или не случайности различий (или сходства). При
этом гипотеза о случайности называется «нуль» гипотезой, а гипотеза о
неслучайности называется альтернативной.
Задание 11. Две группы испытуемых оценивались по 100-балльной шкале.
Определить значимо ли отличаются средние показатели первой группы от
аналогичных показателей второй.
Решение.
H
0
: M (X) = M(Y)
H
1
: M(X) ≠ M(Y)
x y Xср. Yср. X- x
ср
. Y-yср. (X-x
ср
.)
2
(Y-yср.)
2
52 76 55,2 64,94 -3,2 11 10,24 121
42 85 -13,2 20 174,24 400
43 77 -12,2 12 148,84 144
58 74 2,8 9 7,84 81
46 83 -9,2 18 84,64 324
54 73 -1,2 8 1,44 64
54 77 -1,2 12 1,44 144
82 76 26,8 13 718,24 169
61 67 5,8 2 83,64 4
43 49 -12,2 -16 148,84 256
40 42 -15,2 -23 231,03 529
53 48 -2,2 -17 4,84 289
38 86 -17,2 21 295,84 441
50 48 -5,2 -17 27,04 219
66 29 10,8 -36 116,64 1296
92 38 36,8 -27 1354,24 729
64 74 8,8 9 77,44 81
Σ=3436,44 Σ=5361
δx
2
= (Σ (x-x
ср
.)
2
)/ (n-1)
δx
2
= 3436,44 / (17-1) =214,8
δy
2
=(Σ(y-y
cp
.)2)/ (n-1)
δy
2
=5361/16=335.06
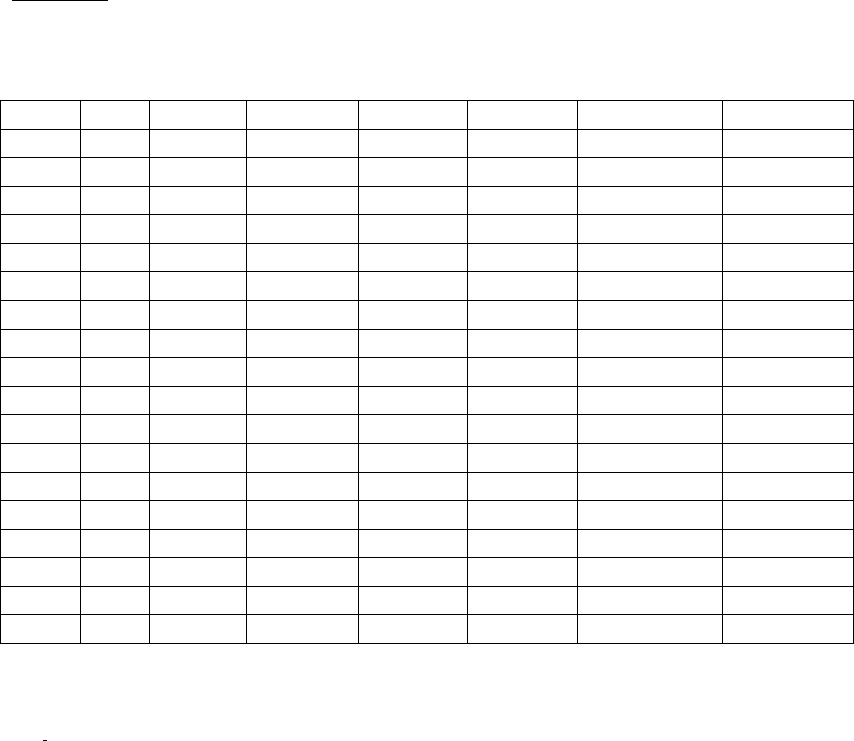
T
набл
. = ((x
ср
.-y)/ ((n-1) *δx
2
+(m-1)* δy
2
))*√(n*m (n+m-2)/(n+m)
T
набл
.= ((55,2-64,94)/(3436,8+5360,96))*√(16*16(16+16-2))/(16+16)= -0,015
Т
Крит.
= (0,05;30) → Т
крит
.= 2,04
T
набл
.< Т
Крит
→ нет значимых различий.
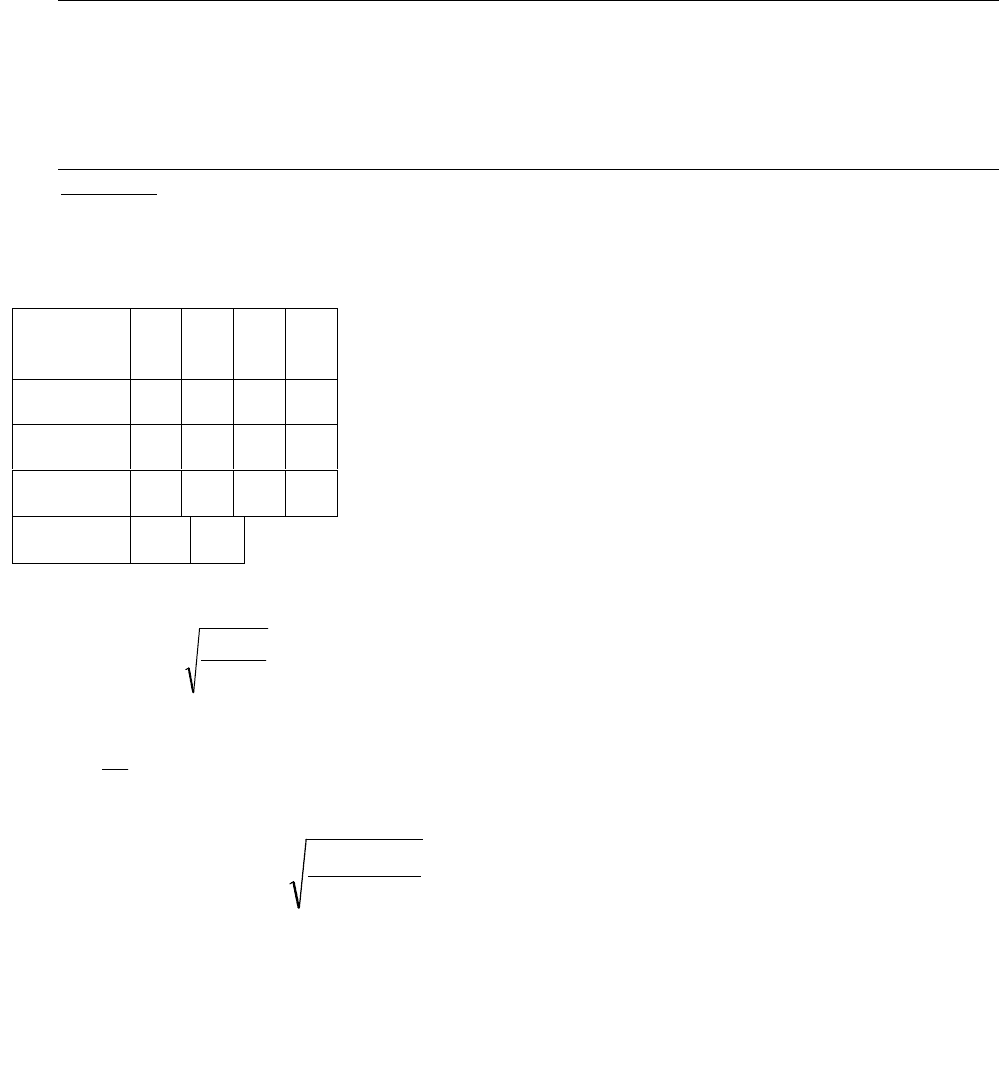
14
Задание 12. В таблице приведены результаты анонимного опроса,
выявляющего отношение опрашиваемых к супружеской измене. Можно ли
утверждать, что женщины более лояльны, чем мужчины? Принять =0,05
Отношение к супругу после измены
Простил Не простил Затрудняюсь с ответом
Отношение мужчины 72 158 93
Отношение женщины 97 168 120
Решение:
H
0
: P
1
=P
2
H
1
: P
1
≠P
2
Pm
Pf
m
f
простил
72 97
0,222
0,212
не простил
158 168
0,489
0,368
затрудняюсь
с ответом
93 120
0,287
0,263
сумма
323
456
21
21
21
*
nn
nn
i
n
Pi
i
456323
456323
368,0489,0*
=1,663797
Для уровня α 05,0
при критическом φ
1,64
Гипотеза Н
1
принимается
15
Задание 13. Группа мужчин и группа женщин были протестированы по
методике WAIS. Можно ли утверждать, что интеллект женщин распределён в
популяции более однородным образом?
М. 129 101 137 112 115 111 123 110 118 103 94 96 116 97 112 100
Ж. 105 98 140 112 130 138 119 120 114 124 112 105 97 117 100 90
Решение:
H
0
: D (X) = D(Y)
H
1
: D(X) ≠ D(Y)
X Y
2
XX
2
YY
129 105 328,6969 77,6161
101 98 97,4169 249,9561
137 140 682,7769 685,9161
112 112 1,2769 3,2761
115 130 17,0569 262,1161
111 138 0,0169 585,1561
123 119 147,1369 26,9361
110 120 0,7569 38,3161
118 114 50,8369 0,0361
103 124 61,9369 103,8361
94 112 284,5969 3,2761
96 105 221,1169 77,6161
116 97 26,3169 282,5761
97 117 192,3769 10,1761
112 100 1,2769 190,7161
100 90 118,1569 566,9161
1774 1821 2231,75 3164,438
110,875 113,8125
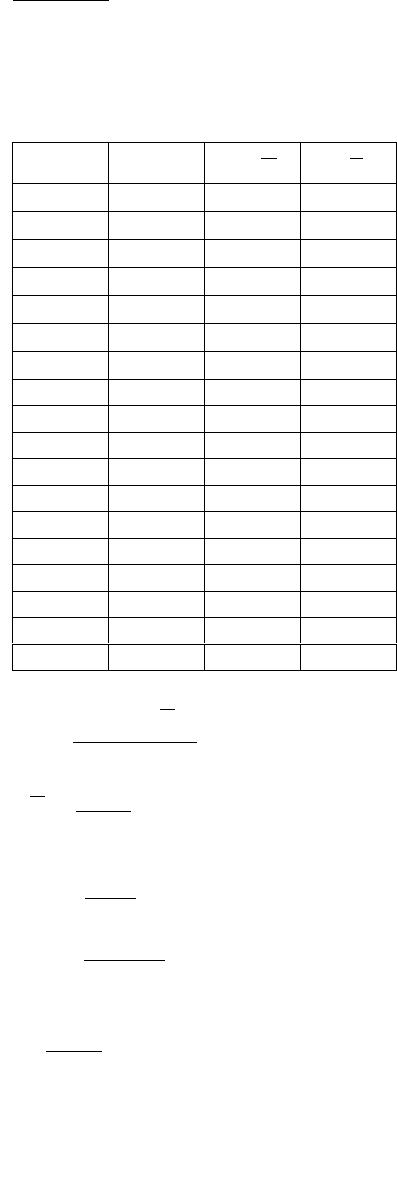
1
2
2
n
iXXi
n
Xi
iX
9.210
15
3164
2
y
78.148
15
75.2231
2
x
F=
9,148
9,210
=1.41
Fkp=2.38
Значимых различий нет
16
Задание 14. Группа испытуемых выполнила два задания на оценку
невербального интеллекта: «Сборка куба» и «Ханойская башня». Результаты
работы над заданием представлены в таблице. Используя критерии
Макнамара проверить на уровне =0,05 гипотезу о том, что не существует
различий в выполнении группой обоих заданий.
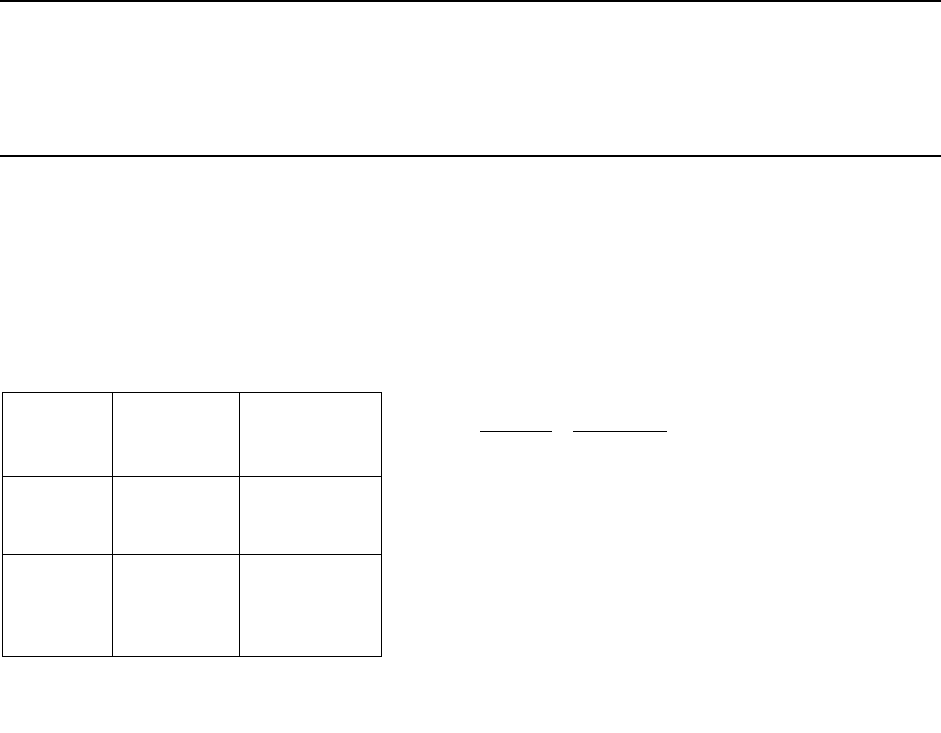
Сборка куба
Верно Неверно
Верно 5a 3b
Ханойская башня
___________________________________________________________________
Неверно 1c 2d
Где a - первая цифра собственного возраста; b - вторая цифра собственного
возраста; c - вторая цифра собственного роста; d - третья цифра собственного
роста.
верно
неверно
верно
52 30
неверно
18 23
Т=
c
b
cb
2
=
48
1830
2
=3
Применимо т.к. в+с>20
Ткр = 1,36
Существуют значимые
различия

3
Позиция № 85
в плане издания
учебной литературы
МГУ на 2004 год
Рецензент В. В. Калита
Составила Светлана Анатольевна Данченко
Решение задач по курсу
«Математические методы в психологии»
Методические указания
Печатается в авторской редакции
1,0 уч. изд. л. Формат 60 84
1
/
16
Тираж 200 экз. Заказ №
Отпечатано в издательско полиграфическом комплексе
МГУ им. адм. Г. И. Невельского
690059, Владивосток, ул. Верхнепортовая, 50а
