Curry G.L., Feldman R.M. Manufacturing Systems Modeling and Analysis

Подождите немного. Документ загружается.

Problems 273

tribution Analysis Algorithm (Property 8.4) is more complicated and is best handled

in Excel with VBA as is the algorithm of Property 8.7. I n this appendix, we give the

Excel formula needed for the Mean Value Analysis Algorithm and leave the exten-

sions to the reader. The material in the Appendix of Chap. 3 can be used to ﬁnd the

relative arrival rates (Property 8.1) of a network. Given the vector r, the following

can be used to obtain the cycle times for the network of Example 8.2.

The initial data of the problem is established by the following.

AB C DE

1 E[Ts-1] E[Ts-2] E[Ts-3]

2 0.2 0.5 0.5

3 r-1 r-2 r-3

4 110.9

We skip a row and then setup for the algorithm.

AB C D E

6 w CT-1 CT-2 CT-3 Sum

7 1 =B2 =C2 =D2

In Cell A8, type =A7+1 and then copy Cell A8 down through Cell A20. In Cell E7,

type

=SUMPRODUCT(B7:D7,$B$4:$D$4)

and copy Cell E7 down through Cell E20. Finally, the main iterative step is typed

into Cell B8 as

=B$2+B$2

$A7

B$4

B7/$E7

and then Cell B8 is copied to the right through Cell D8 and then B8 is copied down

through Cell D20. It is important when typing the various formulas that care is taken

to type the dollar signs ($) exactly as shown since at times the row indicator must

be an absolute address and sometimes the column indicator must be an absolute

address. The resulting spreadsheet should give the Mean Value Algorithm through

a CONWIP level of 14.

Problems

8.1. Find the relative ﬂow rates for the network displayed in Fig. 8.4.

8.2. Find the relative ﬂow rates for the network displayed in Fig. 8.6.

8.3. Re-consider the Example 8.2 and ﬁnd the workstation and system performance

measures for a CONWIP level of

(a) 7 jobs, and

(b) 10 jobs.

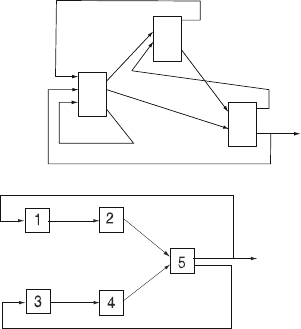
274 8 WIP Limiting Control Strategies

Fig. 8.4 Network ﬂows for

Problem 8.1

4/6

1/6

1/2

1/4

3/4

Fig. 8.5 Network ﬂows for

Problem 8.5

thru

good

bad

8.4. For the network of Problem 8.1, consider a CONWIP level of 5 jobs and as-

sume that each workstation has only one processor. The means of the exponentially

distributed service times at the three workstations are 15 minutes, 30 minutes, and

1 hour, respectively. Using the Mean Value Analysis Algorithm, ﬁnd the expected

cycle time in each workstation, the expected work-in-process in each workstation,

the ﬂow rate for each workstation, the total system throughput, and the system cycle

time.

8.5. Consider the following closed queueing network made up of single server work-

stations with routing structure displayed in Fig. 8.5. Consider that each workstation

has one machine with exponentially distributed processing times. Use the Mean

Value Analysis Algorithm with w

max

= 10 to ﬁnd the expected cycle time in each

workstation, the expected work-in-process i n each workstation, the mean through-

put rate for each workstation, the total system throughput, and the system cycle time.

(a) Use the following data (based on an example in [4]):

E[T

]=(1/2,1/2,1,1,1)

Pr{good} = 1/2,

Pr{bad} = 1/2.

(b) Use the following data:

E[ T

]=(1/3, 1,3/2,1/2,2)

Pr{good} = 1/2,

Pr{bad} = 1/2.

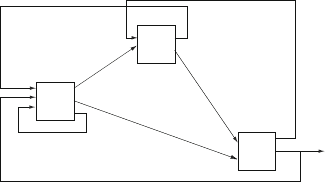
Problems 275

Fig. 8.6 Network ﬂows for

Problems 8.2 and 8.6

6/8

1/8

1/4

3/4

4/5

1/5

E[ T

]=(1/3, 1,3/2,1/2,2)

Pr{good} = 3/4,

Pr{bad} = 1/4.

8.6. Consider the single product network model depicted in Fig. 8.6.

(a) Compute the relative ﬂow rates (r

= 1, r

(b) Let the mean processing times be given by (4 hr, 2 hr, 3 hr) for the three work-

stations and assume that there is only one processor at each workstation. The total

number of jobs kept in the system at all times is 10. Assuming that the cycle time

estimates for the three workstations converge to 32.769 hr, 3.335 hr, and 6.421 hr,

respectively, ﬁll in the following information:

WIP

=?, WIP

= 1.267

=?,

= 0.222,

= 0.197

WIP

=?, th

=?, CT

timates for the three workstations as well as the mean throughput for the factory.

8.7. Consider the single product network model depicted in Fig. 8.7.

(a) Compute the relative ﬂow rates (r

= 1, r

(b) Let the mean processing times be given by (2.5 hr, 3 hr, 5 hr) for the three

workstations and assume that there is only one processor at each workstation. The

total number of jobs kept in the system at all times is 8. Assuming that the cycle time

estimates converge to (8.357 hr, 5.001 hr, 24.951 hr) for the three workstations, ﬁll

in the following information:

WIP

=?, WIP

= 4.563

=?,

= 0.152,

= 0.183

WIP

=?, th

=?, CT

time estimates for the three workstations as well as the mean throughput for the

factory.

276 8 WIP Limiting Control Strategies

Fig. 8.7 Network ﬂows for

Problem 8.7

1/3

1/2

3/4

1/4

8.8. Resolve Problem 8.4, with an additional processor at Workstation 2.

8.9. Resolve Problem 8.5 (a) with 1, 2, 1, 1, 2 servers in the respective workstations.

8.10. Resolve Problem 8.3 except assume that the SCV for all service times is 0.25

with a CONWIP limit of 5 jobs.

8.11. Solve Problem 8.4 except assume that the processing times at the workstations

have the following characteristics:

E[ T

]=(0.25,0.50,1.0) hr

=(0.75,1.25,2.0) .

8.12. Consider a two product production facility with three, single-server worksta-

tions. The WIP limits for the products are 2 and 3 jobs. Assume that the processing

times by product are exponentially distributed with mean times of

Product E[T

(i,1)] E[T

(i,2)] E[T

(i,3)]

i = 1 1.00 hr 2.00 hr 3.00 hr

i = 2 1.75 hr 2.50 hr 1.50 hr

The workstation transition probability matrices for the two products are:

⎡

⎣

1/53/51/5

1/51/53/5

2/52/51/5

⎤

⎦

and p

⎡

⎣

2/63/61/6

3/61/62/6

2/63/61/6

⎤

⎦

(a) Determine the cycle times and WIP’s by product and workstation using the al-

gorithm of Property 8.7.

(b) Compute the product and system performance measures given that the ﬂow out

of Workstation 3 back to Workstation 1 is considered good production for both prod-

ucts.

8.13. Consider Example 8.5 with two products containing routes according to

Figs. 8.2a and 8.2b. Add a third product with its CONWIP level set at 7 jobs in

this facility. The mean processing times (in hours) for the third product in the three

workstations are E[T

(3,k)] = (0.6,0.4,0.5). The workstation transition probability

matrix for this product is

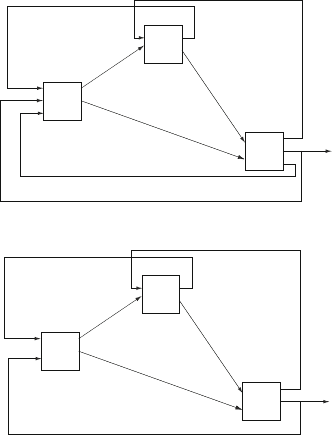
Problems 277

Fig. 8.8a Network ﬂows for

Product 1 of Problem 8.15

2/3

1/3

1/2

8/10

1/10

rework

1/10

output

Fig. 8.8b Network ﬂows for

Product 2 of Problem 8.15

1/2

1/3

2/3

3/4

1/4

output

⎡

⎣

02/31/3

4/501/5

3/41/40

⎤

⎦

Using the approximation algorithm of Property 8.8, determine the cycle times and

WIP levels for each workstation by job type. Assume that the ﬂow from Worksta-

tion 3 to Workstation 1 is good production and determine factory mean throughput

and cycle time.

8.14. Reconsider the facility described in Problem 8.12 except let the WIP limits

for the products be 8 and 10 jobs, respectively. (a) Determine the cycle times and

WIP’s by product and workstation using the algorithm of Property 8.8.

(b) Compute the product and system performance measures given that the ﬂow out

of Workstation 3 back to Workstation 1 is considered good production for both

products.

8.15. A two-product factory is operated by releasing units only when a job is com-

pleted. The company policy is to maintain exactly 8 units of Product 1 and 5 units

of Product 2 in the system at all times. So if a job of type i completes, another job

of that type is immediately released into the factory. The two products have quite

different processing sequences and times with routing structures as displayed in

Figs. 8.8a and 8.8b . All processing times are exponentially distributed. The mean

processing times by workstation and product are

278 8 WIP Limiting Control Strategies

Fig. 8.9a Network ﬂows for

Product 1 of Problem 8.16

2/3

1/3

1/2

8/10

1/10

rework

1/10

output

Product E[T

(i,1)] E[T

(i,2)] E[T

(i,3)]

i = 1 2.0 hr 3.0 hr 1.0 hr

i = 2 1.5 hr 2.0 hr 3.50 hr

Using the provided data, obtain the following answers using the algorithm of Prop-

erty 8.8.

(a) Find the relative arrival rates to the workstations.

(b) Write the equations for the workstation cycle times.

WS 1 WS 2 WS 3

8.543 hr 16.855 hr 8.086 hr

8.275 hr 16.439 hr 9.681 hr

and complete the following tables.

WS 1 WS 2 WS 3

Product 1 WIP

2.566 3.730 1.704

? 0.221/hr 0.211/hr

Product 2 WIP

? 2.036 1.598

0.165/hr 0.124/hr 0.165/hr

(d) Give the workstation utilization factors.

(e) Give the system cycle times and throughputs f or the two products.

8.16. A two-product factory is operated by releasing units only when a job is com-

pleted. The company policy is to maintain exactly 6 units of each product type in the

system at all times. So if a job of type i completes, another job of that type is imme-

diately released into the factory. The two products have quite different processing

sequences and times with routing structures as displayed in Figs. 8.9a and 8.9b .

All processing times are exponentially distributed. The mean processing times by

workstation and product are

Product E[T

(i,1)] E[T

(i,2)] E[T

(i,3)]

i = 1 15min 30min 45min

i = 2 60min 42min 24min

References 279

Fig. 8.9b Network ﬂows for

Product 2 of Problem 8.16

1/2

1/3

2/3

3/4

1/4

output

Using the provided data, obtain the following answers.

(a) Verify the following relative arrival rates.

Product r

i,1

i,2

i,3

i = 1 1 0.737 0.702

i = 2 1 0.5 1.1111

(b) Using the algorithm of Property 8.7, determine the workstation cycle times if the

CONWIP levels were set to w

max

=(1,1).

workstation WIP levels by product for the CONWIP levels of w

max

=(6,6).

(d) Determine the workstation utilization factors.

(e) Determine the system performance measures.

8.17. Resolve Example 8.6 except assume that the service time distribution has a

Gamma distribution with shape parameter

= 2 (i.e., an Erlang-2 distribution) and

with mean values as speciﬁed by Table 8.9.

References

1. Askin, R.G., and Standridge, C.R. (1993). Modeling and Analysis of Manufacturing Systems.

John Wiley & Sons, New York.

2. Buzacott, J.A., and Shanthikumar, G.J. (1993). Stochastic Models of Manufacturing Systems.

Prentice Hall, Englewood Cliffs, N. Y.

3. Curry, G.L., Deuermeyer, B.L., and Feldman, R.M. (1989). Discrete Simulation: Fundamen-

tals and Microcomputer Support. Holden-Day, Inc., Oakland, CA.

4. Diagle, J.N. (1992). Queueing Theory for Telecommunications. Addison-Wesley Publishing

Co., Reading, Mass.

5. Duenyas, I. (1994). A Simple Release Policy for Networks of Queues with Controllable In-

puts, Operations Research, 42:1162–1171.

6. Gross, D., and Harris, C.M. (1998). Fundamentals of Queueing Theory, Third Edition, John

Wiley & Sons, New York.

7. Harrison, J.M., and Wein, L.M. (1990). Scheduling Networks of Queues: Heavy Trafﬁc Anal-

ysis of a Two-Station Closed Network, Operations Research, 38:1052–1064.

8. Hopp, W.J., and Spearman M.L. (1996). Factory Physics: Foundations of Manufacturing

Management. Irwin, Chicago.

280 8 WIP Limiting Control Strategies

9. Marie, R.A. (1979). An Approximate Analytical Method for General Queueing Networks.

IEEE Transactions on Software Engineering, 5:530–538.

10. Marie, R.A. (1980). Calculating Equilibrium Probabilities for

(n)/C

/1/N Queues. Perfor-

mance Evaluation Review, 9:117–125.

11. Reiser, M., and Lavenberg, S.S. (1980). Mean-Value Analysis of Closed Multichain Queuing

Networks. J. Association for Computing Machinery, 27:313–322.

12. Spearman, M.L., Woodruff, D.L., and Hopp, W.J. (1990). CONWIP: A Pull Alternative to

Kanban, International Journal of Production Research, 28:879–894.

13. Wein, L.M. (1990). Scheduling Networks of Queues: Heavy Trafﬁc Analysis of a Two-Station

Closed Network with Controllable Inputs, Operations Research, 38:1065–1078.

14. Wein, L.M. (1992). Scheduling Networks of Queues: Heavy Trafﬁc Analysis of a Multistation

Network with Controllable Inputs, Operations Research, 40:S312–S344.

Chapter 9

Serial Limited Buffer Models

Limited buffer capacity models can be used for the mathematical representations of

a form of kanban control. There are two aspects of limited buffer systems studied

in this chapter. First an approach for developing an analytical approximation model

for serial ﬂow systems is developed. Then the issue of how these buffer values can

be set to yield an optimal system conﬁguration is addressed.

The systems considered here consist of a set of workstations that have limits on

the number of work-in-process units allowed to wait at each of the single-server

processing stations. For serial systems, these workstations are connected in a serial

conﬁguration so that jobs ﬂow from the ﬁrst to the second workstation only, and

then from the second to the third workstation, etc., until they exit the facility. Thus,

all jobs have the same routing sequence. The workstations have a set number of

jobs that are allowed into the workstation simultaneously and these limits need not

be identical. Let w

represent the work-in-process capacity limitation for Worksta-

tion k. This is the total number of jobs allowed in the workstation including the job

being processed. Only single-server machines in each workstation are considered;

the complexities of multiple servers in a limited-buffer capacity model is beyond the

scope of this analysis. (Thus, Workstation k will process jobs on Machine k so the

terms Workstation k and Machine k will be used interchangeably.)

There are several methods of operating a WIP-limiting control strategy. The ma-

jor policy is that a job may not proceed to the next workstation until a space becomes

available in that workstation. However, there are several ways the workstation can

operate. The concept of process blocking after job completion is generally used in

analytical models. That is, when a job is ﬁnished, it may not be removed from the

machine until space is available in the next workstation for this job. This effectively

blocks the machine from processing other jobs in its queue and is called blocking

after service. Another variation is blocking before service, that is the machine can-

not process the job until it has the authorization to move to the next workstation. A

control procedure frequently used in practice processes queued jobs in the worksta-

tion until they all have been processed and the machine is forced to be idle due to

the lack of unﬁnished inventory. In this chapter, only the blocking after processing

strategy is implemented for modeling purposes. This s trategy allows for the imme-

G.L. Curry, R.M. Feldman, Manufacturing Systems Modeling and Analysis, 2nd ed., 281

DOI 10.1007/978-3-642-16618-1

 Springer-Verlag Berlin Heidelberg 2011

282 9 Serial Limited Buffer Models

Fig. 9.1 Network structure

for the kanban analysis

diate response of the system to congestion and does not delay the response until

several more jobs have been processed.

This chapter deals with a ﬁnite WIP control approach where the limits are placed

on the number of jobs allowed in each workstation rather than in the factory as

a whole as was done with the CONWI P approach of Chap. 8. The general ap-

proach is to develop approximate probability distributions for the number of jobs

in each workstation (somewhat) independently and then connect these to estimate

factory performance. To facilitate the individual workstation models, general pro-

cessing time distributions are approximated by easy to model exponential phases

while maintaining the ﬁrst two moments of the general service distributions. By as-

suming that all distributions to be modeled have SCV’s greater than or equal to 1/2,

Coxian (GE

) process sub-models can be used and tractable steady-state queueing

models result. An approximation methodology is developed for serially connected

systems with ﬁnite buffers at each workstation. The methods of this chapter utilize a

decomposition approach that make the resulting models computationally tractable.

9.1 The Decomposition Approach Used for Kanban Systems

The system being modeled is a series of workstations, or machines, connected by

buffer spaces of varying capacities. Job releases into the facility are controlled by

an initial machine with an unlimited backlog that continuously processes jobs and

sends them into the ﬁrst workstation as long as there is space for that job. When the

job cannot proceed into the ﬁrst workstation, the capacity there being full, then this

“job release” machine is blocked using the same “blocked after processing rule” as

all “real” workstation machines. The pre-release jobs are not considered as actual

jobs and do not count as facility WIP. This initial process can be thought of as the

preparation time necessary for a job release. Figure 9.1 illustrates the serial network

structure being studied, where Machine 0 is a machine representing job releases

to the system and there is a buffer of ﬁnite capacity between each machine. It is

possible that job releases are simply due to an individual processing the order so

“machine” may be a misnomer, but it is used simply for ease of reference.

The system can be modeled by developing the steady-state equations deﬁning

the proportion of the time that the system is in every possible state. This direct full

scale modeling approach gets into computational difﬁculty very quickly because the

number of states that have to be considered grows exponentially with the number

of serial workstations. For example, if there can be 5 jobs in each workstation and

there are 4 workstations in series, then each workstation would have states 0, ··· ,5,

and the total number of states necessary to model the network is 6

=1296; whereas