Creagh D., Bradley D. (Eds.) Physical Techniques in the Study of Art, Archaeology and Cultural Heritage. Volume 2

Подождите немного. Документ загружается.

12 D. Creagh

(a)

(b)

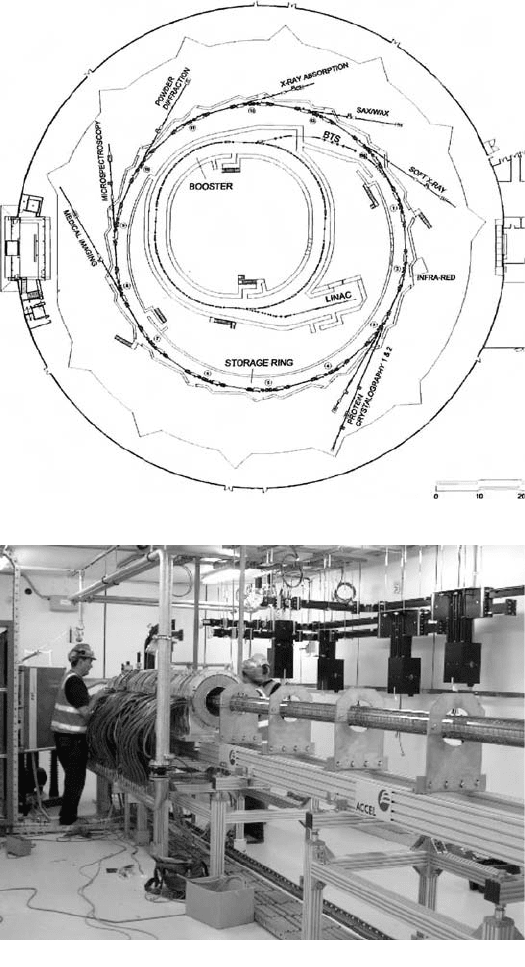
Fig. 4. (a) Floor plan of the Australian Synchrotron. The LINAC accelerates electrons

from a thermionic source to 100 MeV. These electrons then pass into a booster synchro-

tron that accelerates the electron bunches to 3 GeV. These are then diverted into the stor-

age ring where the electron bunches circulate, producing radiation whenever the bunches

are accelerated. (b) Assembling the LINAC at the Australian Synchrotron. Electron bunches

are generated thermionically and accelerated by the linear accelerator to 100 MeV.

Synchrotron Radiation and its Use in Cultural Heritage Studies 13

(c)

(d)

Fig. 4. (c) Dipole magnets surrounding the vacuum chambers in the booster synchrotron

for the Australian Synchrotron. The electrons are accelerated by an applied radiofrequency

field. As they gain energy, the field strength in the dipole magnets is increased to maintain

the electrons in their orbit. (d) A view of a dipole magnet before it is rolled into position

over the vacuum chamber (the curved section on the right of the picture).

dipole magnets, and is the major source of energy loss from the accelerator. When the elec-

tron bunch energy has reached 3 GeV, a “kicker magnet” diverts the electrons in the

booster synchrotron into the synchrotron storage ring. This ring is not circular, but consists

of straight sections connected to curved sections at which the bending magnets are situ-

ated. Additional magnets, a magnetic quadrupole and a magnetic sextupole, are mounted

at the entrance and exit ports of each dipole magnet to steer and focus the electron bunches.

Figure 4(d) shows the positioning of a dipole magnet in the storage ring. Two dipole

magnets exist between neighbouring straight sections; in this case, there are 14 pairs of

dipole magnets. At the right of the picture, the vacuum chamber can be seen. The dipole

magnet is about to be rolled into position around the vacuum chamber. A closer view of

the dipole magnet and its associated sextupole magnet is shown in Fig. 4(e). A magnetic

quadrupole is situated at the far end of the dipole magnet.

2.2.2. Second- and third-generation synchrotrons

Second-generation synchrotrons such as the Photon Factory, Tsukuba, Japan, were built

for dedicated use by scientists, and consist of straight vacuum sections, at the ends of

which are placed bending magnets. In the straight sections, insertion devices, i.e. devices

in which the electron beam is perturbed from the normal orbit, can be placed. These inser-

tion devices comprise a set of magnets of alternating polarity that have the effect of

decreasing the radius of curvature of the electron beam, thereby changing the emission

14 D. Creagh

(e)

Fig. 4. (e) A closer view of the dipole magnet and its associated sextupole magnet (on the

left of the dipole magnet), and the quadrupole magnet (on the right of the dipole magnet),

which are integral components of the storage ring lattice.

characteristics of the source. These periodic magnetic arrays are referred to as undulators

if the radiation emitted by successive bends adds coherently, or as wigglers if the radiation

emitted by successive bends adds incoherently. Wigglers, undulators, and their properties

will be discussed in detail later.

Third-generation synchrotrons are the adaptation of second-generation synchrotrons to

produce small electron beam size and divergence, and the straight sections are optimized

for the inclusion of insertion devices. Figure 5(a) shows schematically the organization of

a modern synchrotron radiation facility, showing how the electron beam may be modified

to produce radiation of different characteristics. Third-generation synchrotrons have their

optics arranged so as to produce electron beams of small size, and the dimensions of the

electron beam source are referred to as s

and s

for the beam sizes in the horizontal and

the vertical directions, respectively. The amount of radiation collected in the horizontal

plane by an experiment depends on the size of the exit apertures in the horizontal plane.

The effective emission angle in the vertical plane is limited to ±1/g of the horizontal plane,

and is approximately

The machine characteristics of the Australian Synchrotron are given in Table 2. The

emittance is a measure of the intrinsic source size of the synchrotron radiation storage ring.

In insertion devices, the electrons travel through a periodic linear magnetic structure. In

such a structure, the magnetic induction may be devised to be sinusoidal and be oriented

normal to the plane of the electron orbit, such that

where l

is the wavelength of the magnetic array. This imposes a sinusoidal motion on the

electron, and this is constrained to the horizontal plane. This is illustrated schematically in

Fig. 5(b). An important parameter describing the motion of the electron is the deflection

parameter K (= eB

/2pmc = 0.934 l

). In terms of K, the maximum angular deflection

from the orbit is d = K/g.

For K£1, radiation from the bends can interfere with one another because the excursion

of the electrons lies within the 1/g limit for the radiation cone. This particular structure

gives rise to undulator radiation.

For K>>1, interference effects are not of importance, and the radiation that emanates

from this structure is referred to as wiggler radiation.

2.2.2.1. Wiggler radiation. K is usually a large number (>10) for periodic magnetic arrays

designed to emit wiggler radiation. In this case, the radiation from different parts of the

electron trajectory add incoherently, and the total flux from the array is 2N times the appro-

priate formula for a bending magnet, with the values of B and R taken at the point of the

Bz B

() cos

⎛

⎝

⎜

⎞

⎠

⎟

⎛

⎝

⎜

⎞

⎠

⎟

⎛

⎝

⎜

⎞

⎠

⎟

570

0.43

Synchrotron Radiation and its Use in Cultural Heritage Studies 15

(a)

(b)

Fig. 5. (a) Schematic representation of the organization of a modern synchrotron radiation

facility, showing how the electron beam may be modified to produce radiation of different

characteristics by the use of insertion devices in the straight sections to modify the trajec-

tory of the electron bunches and the use of bending magnets to divert them in their path.

(b) Electron motion within a periodic magnetic field. The schematic diagram is for an

undulator. These are linear periodic magnetic arrays (situated either inside or outside the

storage ring vacuum vessel) in which the radiation from the bends add together construc-

tively to produce a coherent radiation pattern.

Synchrotron Radiation and its Use in Cultural Heritage Studies 17

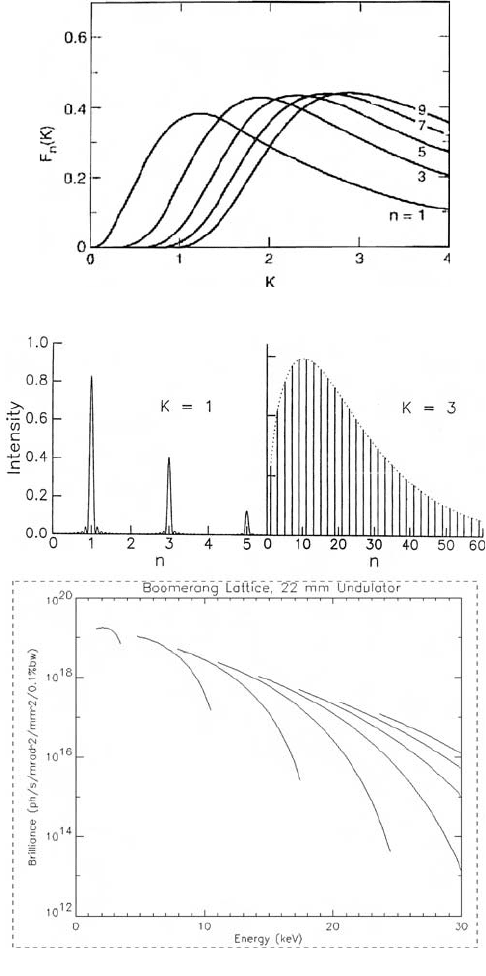
Fig. 5. (c) Plot of F

(K) as a function of K. (d) Relative intensity plots showing the effects

of K on a harmonic number. Shown, as well, are the characteristics of an undulator chosen

for use in the spectromicroscopy beamline at the Australian Synchrotron.

(c)

(d)

18 D. Creagh

e(i)

Fig. 5. (e) (i) Comparative spectral brightness for a number of synchrotron radiation

sources. At the bottom are spectral brightness curves for bending-magnet sources with two

different values of E

, one a soft X-ray source and the other a hard X-ray source. Above

them are plots of the spectral brightness for wigglers mounted in straight sections of the

two storage rings. Note that the radiation from the wigglers is similar in shape to the bending-

magnet sources, but 2N times more intense, and shifted to higher energies. At the top are

curves relating to the spectral brightness of undulators in the straight sections of a low-

energy and a high-energy ring. The dot indicates the peak intensity of radiation from and

undulator at the Australian Synchrotron.

Table 2. Machine and electron beam parameters for the

Australian Synchrotron (0.1 m dispersion optics)

Parameter Value

Energy 3.0 GeV

Circumference 216 m

Current 200 mA

Horizontal size 181 mm (1 sigma)

Vertical size (1% coupling) 45 mm (1 sigma)

Horizontal divergence 197 mrad

Vertical divergence 23 mrad

Bending-magnet field 1.3 T

Emittance 7.33 nm rad

electron trajectory, tangential to the direction of observation. Here, N is the number of

magnetic periods. For a horizontal angle q,

where E

cmax

= 0.665 E

is expressed in GeV and B

in Tesla).

In the horizontal plane (y = 0), the radiation is linearly polarized in the horizontal direc-

tion. As in the case of simple bending-magnet radiation, the direction of polarization

changes as the y changes, but because the elliptical polarization from one half period

combines with the elliptical polarization with the next half period (which has the opposite

sense), the resultant polarization remains linear.

2.2.2.2. Undulator radiation. Figure 5(b) is a schematic representation of an undulator inser-

tion device. Note that a diagram for a wiggler would look the same: the periodic magnetic

array would look similar, but the deflection parameter K (= eB

/2pmc = 0.934 l

)is

ccmax

0.5

() 1

=−

⎛

⎝

⎜

⎞

⎠

⎟

⎛

⎝

⎜

⎞

⎠

⎟

Synchrotron Radiation and its Use in Cultural Heritage Studies 19

Fig. 5. (e) (ii) Streak photograph showing the time structure of the synchrotron radiation

beam.

e(ii)

20 D. Creagh

(f)

(g)

Fig. 5. (f) Normalized intensities of both horizontal and vertical polarization components,

calculated as functions of the product of the vertical angle of observation y and

g (=E/m

). E is the energy of the electron. E

is the critical energy, defined as 0.665 E

where E is expressed in GeV and B is given in Tesla. (g) Schematic representation of a

helical undulator (after Chavanne, 2002). There are four blocks of magnets in the arrays

(A1, A2, A3, and A4) for every undulator period. The directions of the magnetization

within the structures are shown. By moving two opposing magnet arrays with respect to

the other two, the field strengths of the components of the vertical and horizontal magnetic

fields can be varied. This changes the phase relations between the two impressed oscilla-

tions, thereby changing the polarization of the electron beam.

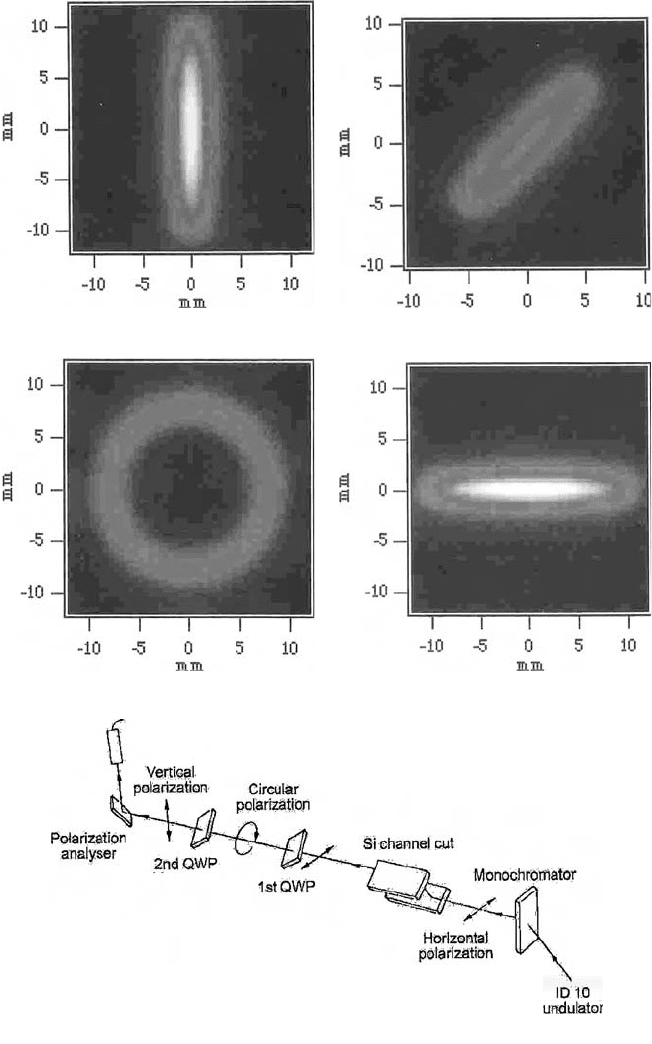
Synchrotron Radiation and its Use in Cultural Heritage Studies 21

(i)

h(i) h(ii)

h(iii) h(iv)

Fig. 5. (h) (i) Linear polarization, vertical orientation. (ii) Linear polarization from a

helical undulator inclined at 45∞ to vertical. (iii) Circular polarization.