Cottingham W.N., Greenwood D.A. An Introduction to the Standard Model of Particle Physics
Подождите немного. Документ загружается.


Hints to selected problems 259
11.5 Consider
U = cos αI + i sin ατ · ˆα (see B.9).
Then
U
∗
= cos αI − i sin α(τ
1
ˆα
1
− τ
2
ˆα
2
+ τ
3
ˆα
3
)
and
τ
2
U
∗
= [cos αI + i sin α(τ
1
ˆα
1
+ τ
2
ˆα
2
+ τ
3
ˆα
3
)]τ
2
using
τ
2
τ
1
=−τ
1
τ
2
,τ
2
τ
3
=−τ
3
τ
2
.
Hence
iτ
2
U
∗
= U(iτ
2
) and iτ
2
=
01
−10
.
The result follows.
11.6 Using (B.9).
U = cos αI + sin α(sin φτ
1
+ cos φτ
2
)
=
cos α i sin α(sin φ − i cos φ)
i sin α(sin φ +i cos φ) cos α
.
Chapter 12
12.2 Take the two fields to be
L =
L
1
L
2
.
To maintain local gauge invariance, the dynamical term in the Lagrangian density
must be L
†
˜σ
µ
i(∂
µ
+ i(g
2
/2)W
µ
)L.
There are terms which mix L
1
and L
2
, for example,
−(g
2
/2)L
1
†
˜σ
µ
(W
µ
1
− iW
µ
2
)L
2
=−(g
2
/2)L
1
†
˜σ
µ
L
2
W
µ
†
.
The operator W
µ
†
destroys electric charge e,sothat to conserve charge L
1
†
˜σ
µ
L
2
,
must create charge e.
12.3 The Higgs particle at rest has zero momentum and zero angular momentum. Hence
the e
+
and e
−
have opposite momentum. If they had opposite helicities, they would
have to carry orbital angular momentum with a component +1or−1 along their
direction of motion, to conserve angular momentum. This is not possible since
p · (r × p) = 0.
The final density of momentum states is
ρ(E) =
V
(2π)
3
4π p
e
2
d p
e
dE
.

260 Hints to selected problems
The final energy E = 2E
e
,where E
e
2
= m
e
2
p
e
2
. Hence
d p
e
dE
=
1
2
d p
e
dE
e
=
E
e
2 p
e
, and p(E) =
V
(2π)
2
p
e
E
e
.
The interaction term in (12.9)is−(c
e
√
2)h
¯
ψψ. From (6.24) and (3.21), this gives
f |V |i=
1
√
V
1
√
2m
H
m
e
E
e
[¯µ
+
(p)v
+
(−p)]
or
[¯µ
−
(p)v
−
(−p)].
Now ¯µ
±
(p)v
±
(−p) = sinh θ , and E
e
/m
e
= cosh θ . Hence the decay rate to positive
helicities is
2π| f |V |i|
2
ρ(E) = 2π
c
e
2
2
1
2m
H
tanh
2
θ
1
(2π)
2
p
e
E
e
.
Also tan θ = v
e
/c = p
e
/E
e
and E
e
= m
H
/2. The decay rate to negative helicities is
the same, and the result follows.
12.4 Since c
τ
> c
µ
> c
e
(see (12.13)) the decay to τ
+
τ
−
dominates in the leptonic partial
width. Also, since the Higgs mass is much greater than the τ mass, v
τ
≈ c. Hence
m
H
≈
c
2
τ
16π
=
1
16π
m
τ
φ
0
2
.
Chapter 13
13.1 In the rest frame of the W, and neglecting the lepton mass, p
1
=−p
v
, E
l
= p
l
=
M
w
/2, and p
i
2
= M
w
2
/4 = p
x
2
+ p
y
2
+ p
z
2
.Taking the x-axis to be the beam direc-
tion, the mean square transverse momentum is
p
x
2
+ p
y
2
= (2/3) p
l
2
= M
w
2
/6.
13.2 From (12.23), the Z
µ
is produced by right-handed electron fields with a cou-
pling e tan θ
w
= 2 e sin
2
θ
w
/ sin(2θ
w
) and by left-handed fields with a coupling
−e cos(2θ
w
)/ sin(2θ
w
). In head-on collisions at high energies the right-handed com-
ponent of the electron (positron) has positive (negative) helicity. Hence the total spin
is +1 along the electron beam direction. The spin of the left-handed components is
opposite. For unpolarised beams the left-handed and right-handed components are
equally populated, and the result follows.
13.3 Consider the decay W
−
→ e
−
+ ¯ν
e
in the W
−
rest frame. With no loss of general-
ity we may take the W
−
to have J = 1, J
z
= 0 (see Section 4.9). The interaction
Lagrangian density responsible for the decay is (from (12.15) and (12.16))
L =−(g
2
/
√
2) j
3
W
−
3
.

Hints to selected problems 261
If the electron has momentum p, the neutrino has momentum −p.Neglecting the
electron mass (see Problem 6.5) the matrix element for the decay is
f
|
V
|
i
=
g
2
√
2
1
√
2M
w
V
−
|
σ
3
|
+
.
(Recall σ·p
|
−
=−
|
−
,σ· (−p)
|
+
=−
|
+
.) Also, from Problem 6.6,
−
|
σ
3
|
+
=−sin θe
iφ
. The decay rate is
= 2π
|
f
|
V
|
i
|
2
d
V
(2π)
3
p
e
2
d p
e
dE
where d p
e
/dE = 1/2, p
e
= M
w
/2, giving
=
g
2
2
48π
M
w
=
G
F
M
w
3
6π
√
2
, by (12.22).
The decay rate for Z → ν ¯ν requires a similar calculation, with M
w
replaced
by M
z
and the coupling constant g
2
/
√
2 replaced by e/ sin 2θ
w
= g
2
/2 cos θ
w
=
g
2
M
z
/2M
w
.(We have used (12.23), (11.38) and (11.37a).) Then
(Z → ν
¯
ν) =
G
F
M
3
z
12π
√
2
.
There are two terms in (12.23) contributing to (Z → e
+
e
−
), yielding
(Z → e
+
e
−
) = (Z → ν ¯ν)[(2 sin
2
θ
w
)
2
+ (cos 2θ
w
)
2
].
13.4 83.86 MeV.
Chapter 14
14.3 Under an SU(2) transformation, and from Appendix A.2
(
T
εL) → (
T
U
T
εUL)
U
T
εU =
U
AA
U
BA
U
AB
U
BB
01
−10
U
AA
U
AB
U
BA
U
BB
=
0 Det(U)
−Det(U)0
= (Det(U))ε
= ε, since Det(U) = 1. Hence (Φ
T
U
T
εUL) = (Φ
T
εL)
14.4 From (11.23),
Φ =
0
φ
0
+h/
√
2
.
Inserting this in (14.6)gives the coupling terms
−(1/
√
2)
[G
d
ij
d
†
Li
d
R j
h + Hermitian conjugate.
Similar terms arise from (14.9) and (14.10). Using the true quark masses these
become
−(1/
√
2φ
0
)
[m
d
i
(d
†
Li
d
Ri
+ d
†
Ri
d
Li
) + m
u
i
(u
†
Li
u
Ri
+ u
†
Ri
u
Li
)]h.
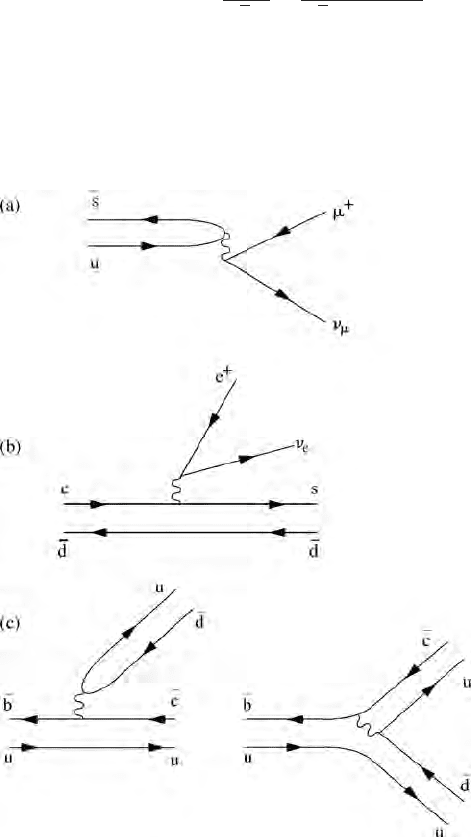
262 Hints to selected problems
The coupling to the top quark is
c
t
=
m
t
√
2φ
0
≈
180 GeV
√
2 × 180 GeV
≈ 0.7.
14.5 For K
+
→ µ
+
+ ν
µ
, the terms
s
L
†
˜σ
µ
u
L
V
∗
us
from j
µ
,ν
µL
†
˜σ
µ
µ
L
from j
µ†
contribute in the second order of perturbation theory. (See (a).)
For D
+
→ K
0
+ e
+
+ ν
e
,
s
†
L
˜σ
µ
c
L
V
∗
cs
from j
µ
,ν
†
eL
˜σ
µ
e
L
from j
µ†
. (See (b).)
For B
†
→
¯
D
0
+ π
†
,
b
†
L
˜σ
µ
c
L
V
∗
cb
from j
µ
, u
†
L
˜σ
µ
d
L
V
ud
from j
µ†
. (See (c).)
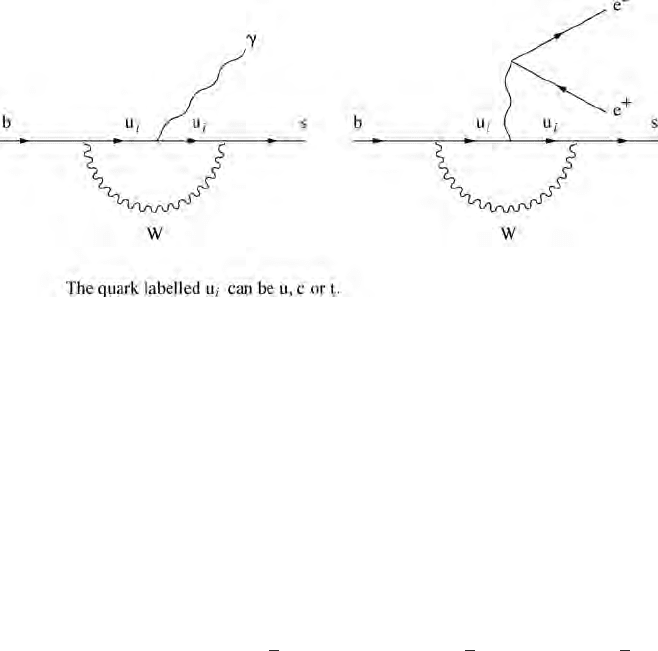
Hints to selected problems 263
14.6
Chapter 15
15.1 The decay rate for Z → d
¯
dof(15.3) can be compared with the decay rate for
Z → e
+
e
−
of (13.3), calculated in the answer to Problem 13.3. Comparing the inter-
action Lagrangian densities (12.23) and (14.14), the term in the left-handed coupling
cos 2θ
w
= 1 −2 sin
2
θ
w
is replaced by (1 − (2/3) sin
2
θ
w
), and in the right-handed
coupling 2 sin
2
θ
w
is replaced by (2/3) sin
2
θ
w
. Including a colour factor of 3 and
replacing sin
2
θ
w
by (1/3) sin
2
θ
w
in the rate (13.3)gives the rate (15.3).
Similarly for Z → u¯u. Comparing (12.23) with (14.14), sin
2
θ
w
is replaced by
(2/3) sin
2
θ
w
.
The decay rate W
+
→ u
i
¯
d
j
of (15.6) can be compared with the rate W
+
→ e
+
ν
e
of (13.2) calculated in the answer to Problem 13.3. Comparing the interactions
(12.18) and (14.20), g
2
/
√
2isreplaced by eV
ij
/
√
2 sin θ
w
= g
2
V
ij
/
√
2. Including
the colour factor of 3, the rate (15.6) follows from the rate (13.2).
Chapter 16
16.1
G
µν
= ∂
µ
G
ν
− ∂
ν
G
µ
+ ig(G
µ
G
ν
− G
ν
G
µ
)
= (∂
µ
G
a
ν
− ∂
ν
G
a
µ
)(λ
a
/2)
+i(g/4)
#
G
b
µ
G
c
ν
λ
b
λ
c
− G
c
ν
G
b
µ
λ
c
λ
b
$
,
and
(λ
b
λ
c
− λ
c
λ
b
) = 2i f
bca
λ
a
(see (B.27)).
Hence
G
µν
= [(∂
µ
G
a
ν
− ∂
ν
G
a
µ
) − gf
abc
G
b
µ
G
c
ν
](λ
a
/2).
16.2 These are the terms in (16.9) cubic and quadratic in the G fields.

264 Hints to selected problems
16.3 Variation of G
a
ν
gives
δS =
− (1/2)G
aµν
δG
a
µν
− g
f
¯q
f
γ
ν
δG
a
ν
(λ
a
/2)q
f
d
4
x,
and
−(1/2)G
aµν
δG
a
µν
=−G
aµν
∂
µ
(δG
a
ν
) + gG
cµν
G
b
µ
δG
a
ν
f
cba
.
(There are two equal contributions to the right-hand side.) Integrating by parts gives
δS =
∂
µ
G
aµν
− gG
cµν
G
b
µ
f
abc
− g
f
¯
q
f
γ
ν
(λ
a
/2)q
f
δG
a
ν
d
4
x
( f
cba
=−f
abc
).
Since the δG
a
ν
are arbitrary (16.14)isobtained.
16.4
Q
2
/4m
2
= e
12x
2
/e
2
= e
3π/α
= 10
560
.
2m ∼ 1 MeV, Q
2
∼ 10
560
(MeV)
2
.
16.5 Take Q·r = Qr cos θ and d
3
Q = Q
2
dQd(cos θ )dφ where (Q,θ,φ) are the polar
coordinates of Q, with r taken to be (0, 0, r).
Chapter 18
18.1
From (14.15), the interaction terms in ¯udW
+
and ¯usW
+
contain factors V
ud
and
V
us
, respectively. Problem (9.10) shows α
K
/α
π
≈ 0.28. Setting this equal to V
us
/V
ud
gives sin θ
12
≈ 0.27.

Hints to selected problems 265
18.2 The internal wave function of two pions at r
1
and r
2
in an S state is a function of
only |r
1
−r
2
| and |r
1
−r
2
| is invariant under both C and P. Hence
CP
)
)
π
0
π
0
(
=
)
)
π
0
π
0
(
and CP
)
)
π
+
π
−
(
=
)
)
π
+
π
−
(
.
18.3 The internal wave function of three pions at r
1
, r
2
, r
3
, depends only on two relative
coordinates, say r
12
= r
2
− r
1
and r
23
= r
3
− r
2
.Tobeinvariant under rotations (J =
0) the internal wave function can be a function of only three scalars: r
12
· r
12
, r
12
· r
23
,
and r
23
· r
23
. These are invariant under C and P. Since the intrinsic parity of the π
0
is negative,
CP
)
)
π
0
π
0
π
0
(
=−
)
)
π
0
π
0
π
0
(
.
18.4 The area of the triangle formed by the origin and the points r
1
= (x
1
, y
1
, 0) and
r
2
= (x
2
, y
2
, 0) is
(1/2)|r
1
× r
2
|=(1/2)|x
1
y
2
−x
2
y
2
)|
= (1/2)|Im(z
∗
1
z
2
)|,
where z
1
= x
1
+ iy
1
, z
2
= x
2
+ iy
2
. Hence the area of the unitary triangle is
(1/2)|Im(V
∗
ud
V
ub
V
cd
V
∗
cb
)|=J/2.
18.5 All the complex numbers z
i
are transformed to z
1
i
= e
i(θ
d
−θ
b
)
z
i
and the triangle is
rotated through an angle (θ
d
− θ
b
).
Chapter 19
19.2 (a) (U
∗
β j
U
αj
U
βi
U
∗
αi
) = (U
∗
βi
U
αi
U
β j
U
∗
αj
)
∗
hence
Im(U
∗
β j
U
αj
U
βi
U
∗
αi
) =−Im(U
∗
βi
U
αi
U
β j
U
∗
αj
).
(b) Since U is unitary,
i
F
βαij
= Im(∂
αβ
U
β j
U
∗
αj
) = Im(|U
αj
|
2
) = 0.
As two examples F
βα12
+ F
βα32
= 0 and F
βα13
+ F
βα23
= 0.
Hence F
βα12
+ F
βα23
= F
βα31
.
(c)
i> j
F
µei j
sin(
m
2
ij
L
2E
) =−J
sin(
m
2
21
L
2E
) + sin(
m
2
32
L
2E
)
−sin(
(m
2
21
+ m
2
32
)L
2E
)
and the result follows.
Chapter 21
21.1 Let
iσ
2
ν
∗
†
σ
µ
∂
µ
iσ
2
ν
∗
= E
Inserting explicit spinor indices
E =ν
i
σ
2
ij
σ
µ
jk
σ
2
kl
∂
µ
ν
∗
l
, (repeated indices summed).
266 Hints to selected problems
But from the algebra of Pauli matrices σ
2
ij
σ
µ
jk
σ
2
kl
= ˜σ
µ
li
.Taking account of the
anticommuting spinor fields E =−∂
µ
ν
∗
l
˜σ
µ
li
ν
i
. and discarding a total derivative that
makes no contribution to the action
E = ν
∗
l
˜σ
µ
li
∂
µ
ν
i
= ν
†
˜σ
µ
∂
µ
ν.
21.2 Inserting explicit spinor indices
ν
T
α
σ
2
ν
β
= ν
αi
σ
2
ij
ν
β j
=−ν
αi
σ
2
ji
ν
β j
= ν
β j
σ
2
ji
ν
αi
= ν
T
β
σ
2
ν
α
.
21.3 From (21.15)
U
M
β j
U
M∗
αj
= U
D
β j
e
ij
U
D∗
αj
e
−ij
= U
D
β j
U
D∗
αj
.
Appendix A
A.1 The equation holds for αβ . ..ν = 1, 2,...,n. Interchanging, say, α and β is equiv-
alent to interchanging column i with column j, and gives the same sign change.
A.3 M = (M + M
†
)/2 + i(M − M
†
)/2i. (M + M
†
)/2isHermitian, as is (M − M
†
)/2i.
A and B, and hence M, can be diagonalised by the same transformation if and only if
AB − BA = 0, i.e. (M + M
†
)(M − M
†
) − (M − M
†
)(M + M
†
) = 0
or
M
†
M − MM
†
= 0.
(This condition is satisfied if M is unitary.)
A.4 Since (MM
†
)
†
= MM
†
,wecan find U
1
such that U
1
(MM
†
)U
†
1
= M
D
2
. M
D
2
has
diagonal elements ≥ 0, since M
D
2
= U
1
M(U
1
M)
†
. Thus we can choose M
D
with
real diagonal elements ≥ 0. If none are zero, M
D
can be inverted. We may then define
H = U
1
†
M
D
U
1
= H
†
, and V = H
−1
M.
Hence
VV
†
= H
−1
MM
†
H
−1
since (H
−1
)
†
= H
−1
= H
−1
U
1
†
M
D
2
U
1
H
−1
= U
1
†
M
D
−1
U
1
U
1
†
M
D
2
U
1
U
1
†
M
D
−1
U
1
= I, since U
1
U
1
†
= I.
Thus V is unitary, as is U
1
V = U
2
.
Finally, M = HV = U
1
†
M
D
U
1
V = U
†
1
M
D
U
2
.
Appendix B
B.1 A unitary transformation, H → H
= VHV
†
= H
D
, say, also diagonalises each term
of U and hence
U → U
= VUV
†
= U
D
= exp(iH
D
).
Hints to selected problems 267
det U = det U
D
=
8
n
exp i(H
D
)
nn
= exp
i
n
(H
D
)
nn
= exp[iTr H
D
].
But TrH
D
= TrH. Hence if Tr H = 0, det U = 1.
B.2 The SU(2) matrices corresponding to R
01
(θ) and R
02
(θ) are respectively
cos(θ/2) i sin(θ/2)
i sin(θ/2) cos(θ/2)
and
cos(θ/2) sin(θ/2)
−sin(θ/2) cos(θ/2)
and the correspondence can be checked directly.
B.3 From equation (B.5), using (B.12) and Problem B.2, R(ψ,θ,φ) corresponds to the
product
e
iψ/2
0
0e
−iψ/2
cos(θ/2) sin(θ/2)
−sin(θ/2) cos(θ/2)
e
iφ/2
0
0e
−iφ/2
.
B.4 Under a Lorentz transformation, l → l
= Ml, r → r
= Nr.
Hence
l
†
˜σ
µ
σ
ν
r → l
†
M
†
˜σ
µ
σ
ν
Nr
= l
†
M
†
˜σ
µ
MN
†
σ
ν
Nr since MN
†
= I
= l
†
L
µ
λ
˜σ
λ
L
ν
ρ
σ
ρ
r from (B.17) and (B.18)
= L
µ
λ
L
ν
ρ
(l
†
˜σ
λ
σ
ρ
r).
It is easy to verify that
˜σ
µ
σ
ν
+ ˜σ
ν
σ
µ
=
0ifµ = ν,
2ifµ = ν = 0,
−2ifµν = i; i = 1, 2, 3.
B.5 Equation (B.10) gives
X(x) = x
i
σ
i
X
(x
) = x
i
σ
i
= R
i
j
x
j
σ
i
.
Also X
= UXU
†
= Ux
j
σ
j
U
†
. The x
j
are arbitrary. Hence Uσ
j
U
†
= R
i
j
σ
i
. Multi-
plying on the left by σ
k
and taking the trace,
Tr(σ
k
Uσ
j
U
†
) = R
i
j
Tr(σ
k
σ
i
).
Now
Tr(σ
k
σ
i
) =
2ifk = i,
0ifk = i.
Hence the result.

268 Hints to selected problems
B.6 From (B.17), M
†
˜σ
µ
M = L
µ
λ
˜σ
λ
. Multiplying on the left by ˜σ
ν
and taking the trace,
the result follows, since
Tr( ˜σ
ν
˜σ
λ
) =
2ifλ = ν,
0ifλ = ν.
Appendix C
C.2 The ground state is given by a|0=0, or (X + iP)|0=0. In the Schr¨odinger rep-
resentation. P =−id/dX,sothat (X + d/dX )ψ
0
= 0, giving ψ
0
= Ae
−X
2
/2, where
the constant A is determined by normalisation.
C.3
N
i
b
i
†
|0=b
i
†
b
i
b
i
†
|0
= b
i
†
(1 − b
i
†
b
i
)|0=b
i
†
|0.
Appendix D
D.1 Q
2
= (p − p
)
2
− (E − E
)
2
= (p
2
− E
2
) + ( p
2
− E
2
) − 2p·p
+ 2EE
.
But E
2
= p
2
+ m
2
, E
2
= p
2
+ m
2
,sothat, neglecting electron masses,
Q
2
=−2 pp
cos θ + 2EE
= 2EE
(1 − cos θ ) = 4EE
sin
2
(θ/2).
The energy and momentum of the recoil proton are given by E
p
= M +
E − E
, P = p − p
; also E
p
2
= M
2
+ P
2
. Hence
Q
2
= p
2
− (E − E
)
2
= (M + E − E
)
2
− M
2
− (E − E
)
2
= 2M(E − E
)
so that (D.3) follows.
D.3 Q
2
= 2EE
(1 − cos θ )
ν = E − E
dQ
2
dν =
∂(Q
2
,ν)
∂(cos θ, E
)
d(cos θ)dE
where the Jacobian of the transformation is
)
)
)
)
−2EE
2E(1 − cos θ)
0 −1
)
)
)
)
= 2EE
.
Hence the result.
