Coondoo I. (ed.) Ferroelectrics
Подождите немного. Документ загружается.


Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations 5
In (2) we proved that the source distance, D, is a metric on the set of all trapezoidal fuzzy
numbers.
Definition 3.3 For a nonnegative integer j, we define j
th
-source number by
I
j
:=
1
0
r
j
s(r)dr.(3.3)
Lemma 3.1 Let I
j
be the j
th
-source number, then {I
j
} is a positive decreasing sequence, where I
0
=
1
2
.
i.e. 0
≤ ...< I
2
< I
1
< I
0
=
1
2
.
Proof: By using the definition of j
th
-source number and regular reducing function we have
I
0
=
1
2
. By Mean Value Theorem for integrals for any integer j ≥ 1, there exists a ψ ∈ (0,1),
such that
I
j
= ψ
1
0
r
j−1
s(r)dr < I
j−1
.
Definition 3.4 For
˜
u,
˜
v ∈F(R),wedefinem-source distance of
˜
uand
˜
vby
D
m
(
˜
u,
˜
v
) :=
1
2
d
H
([
˜
u
]
1
,[
˜
v
]
1
)+
m−1
∑
k=0
d
k
(
˜
u,
˜
v
).
where
m−1
∑
k=0
is defined by
m−1
∑
i=0
a
i
=
1
2
a
0
+
m−1
∑
i=1
a
i
.
Theorem 3.2 For
˜
u,
˜
v,
˜
w,
˜
z
∈F(R), the distance, D
m
, satisfies the following properties:
1. D
m
(
˜
u,
˜
u
)=0,
2. D
m
(
˜
u,
˜
v
)=D
m
(
˜
v,
˜
u
),
3. D
m
(
˜
u,
˜
v
) ≤ D
m
(
˜
u,
˜
w
)+D
m
(
˜
w,
˜
v
),
4. D
m
(k
˜
u, k
˜
v)=|k|D
m
(
˜
u,
˜
v
) for k ∈ R,
5. D
m
(
˜
u
+
˜
w,
˜
v
+
˜
z
) ≤ D
m
(
˜
u,
˜
v
)+D
m
(
˜
w,
˜
z
).
Example 3.1 For two crisp real numbers a and b we have
D
m
(a, b)=|a − b|.
Proposition 3.3 The fuzzy number
˜
v
∗
is a nearest approximation of
˜
uoutofPF
m
(R) if and only if
D
m
(
˜
u,
˜
v
∗
)= min
˜
v
∈PF
m
(R)
D
m
(
˜
u,
˜
v
).(3.4)
We denote the set of all the nearest approximations of a fuzzy number
˜
u,outof
PF
m
(R),by
N
∗
PF
m
(R)
m
(
˜
u
).
437
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations
437
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations

6 Ferroelectrics
Theorem 3.4 Let
˜
ubeafuzzynumber.Ifforpositiveintegermwehaveu, u ∈ C
m−1
[0, 1],then
˜
vis
the nearest approximation of
˜
uoutof
PF
m
(R) if and only if D
m
(
˜
u,
˜
v
)=0.
Proof: See (2).
Theorem 3.5 Let m be a positive integer and suppose that
˜
u ∈F(R) be an arbitrary fuzzy number.
˜
v
∈PF
m
(R) is the nearest approximation of
˜
uoutofPF
m
(R), if and only if for k = 0,...,m −1;
˜
v
and
˜
u have the same k-validity and k-unworthiness and furthermore
[
˜
u
]
1
=[
˜
v
]
1
.
Proof: See (2).
Corollary 3.6 Let
˜
u be a generalized LR fuzzy number. If for positive integer m we have u, u ∈
C
m−1
[0, 1], then the nearest approximation of
˜
uoutofPF
m
(R) exists.
Theorem 3.7 (10) The nearest approximation of a m-degree polynomial-form fuzzy number, out of
PF
m
(R), is itself.
Proof: Let
˜
v ∈PF
m
(R) be the nearest approximation of
˜
u ∈PF
m
(R).Alsolet
v
(r)=d
m
r
m
+ ...+ d
1
r + d
0
,
and
u
(r)=c
m
r
m
+ ...+ c
1
r + c
0
,
By defining w
(r)=v(r) −u(r)=
∑
m
j
=0
a
j
r
j
,wherea
j
= c
j
−d
j
for j = 0,1, . .. , m;wehavew(1)=
0and
1
0
w
(k)
(r)s(r)dr = 0, k = 0,1, . .. , m − 1.
Therefore we have a homogenous system of linear equations with the following nonsingular
coefficients matrix
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
11 1 1
··· 1
I
0
I
1
I
2
I
3
··· I
m
0 I
0
2I
1
3I
2
··· mI
m−1
002I
0
3!I
1
··· m(m − 1)I
m−2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
00 0 0
··· m!I
1
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
Therefore w
≡ 0. i.e. u
≡ v. In a similar way u ≡ v.Thus
˜
u =
˜
v.
Corollary 3.8 D
m
(.,.) is a meter on PF
m
(R).
Lemma 3.9 (10) Let
˜
u be a fuzzy number. For all m
≥ 1 if N
∗
PF
m
(
˜
u
) is not empty, then we have
|N
∗
PF
m
(R)
m
(
˜
u
)| = 1.
Proof: Let
˜
u
∗
1
and
˜
u
∗
2
be two nearest approximations of a fuzzy number
˜
u out of PF
m
(R).
Thus D
m
(
˜
u
∗
1
,
˜
u)=D
m
(
˜
u
∗
1
,
˜
u)=0, and we have
D
m
(
˜
u
∗
1
,
˜
u
∗
2
) ≤ D
m
(
˜
u
∗
1
,
˜
u)+D
m
(
˜
u,
˜
u
∗
2
)=0.
From lemma 3.7 we have
˜
u
∗
1
=
˜
u
∗
2
.
438
Ferroelectrics
438
Ferroelectrics

Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations 7
Corollary 3.10 Let
˜
u be a l-degree polynomial-form fuzzy number where l ≤ m. If
˜
v
∗
be the nearest
approximations of
˜
uoutof
PF
m
(R),then
˜
v
∗
=
˜
u.
Lemma 3.11 (10) Let
˜
u
∗
and
˜
v
∗
be the nearest approximations of two fuzzy numbers
˜
uand
˜
v,
respectively. Then we have
D
m
(
˜
u
∗
,
˜
v
∗
)=D
m
(
˜
u,
˜
v
)
Proof: We have
D
m
(
˜
u
∗
,
˜
v
∗
) ≤ D
m
(
˜
u
∗
,
˜
u)+D
m
(
˜
u,
˜
v
)+D
m
(
˜
v,
˜
v
∗
)=D
m
(
˜
u,
˜
v
).
In a similar way D
m
(
˜
u,
˜
v
) ≤ D
m
(
˜
u
∗
,
˜
v
∗
).
Lemma 3.12 (10) Let
˜
vand
˜
u be t wo fuzzy numbers where u, v, u, v ∈ C
m−1
[0, 1].IfD
m
(
˜
u,
˜
v
)=0,
then there are two sequences of points
{δ
i,k
}
m−1
k
=0
,i= 1, 2 such that for k = 0, 1, ···,m −1,
u
(k)
(δ
1,k
)=v
(k)
(δ
1,k
),
and
u
(k)
(δ
2,k
)=v
(k)
(δ
2,k
).
Proof: Let for two fuzzy numbers
˜
v and
˜
u we have D
m
(
˜
u,
˜
v
)=0. Thus for k = 0, 1, . . . , m − 1,
we have
[
˜
u
]
1
=[
˜
v
]
1
,
val
k
(
˜
v
)=val
k
(
˜
u
), k = 0,...,m −1,
amb
k
(
˜
v
)=amb
k
(
˜
u
), k = 0,...,m −1,
Therefore
1
0
s(r)[u
(k)
(r) − v
(k)
(r)] dr = ±
1
0
s(r)[u
(k)
(r) − v
(k)
(r)] dr, k = 0,...,m −1,
Thus
1
0
s(r)[u
(k)
(r) −v
(k)
(r)]dr = 0, k = 0,...,m − 1,
1
0
s(r)[u
(k)
(r) −v
(k)
(r)]dr = 0, k = 0,...,m − 1.
Thus by Mean Value Theorem for integrals, for any k
= 0, 1, . . . , m − 1, there are two numbers
δ
1,k
and δ
2,k
such that
u
(k)
(δ
1,k
)=v
(k)
(δ
1,k
),
u
(k)
(δ
2,k
)=v
(k)
(δ
2,k
).
4. Properties of m−source distance
Some properties of the approximation operators are presented by Grzegorzewski and
Mr
´
owka (28). In this section we consider some properties of the approximation operator
suggested in Section 3.
Let T
m
: F(R) −→ P F
m
(R) be the approximation operator which produces the nearest
approximation fuzzy number out of
PF
m
(R) to a given original fuzzy number using
Theorem 3.5. Almost all of the theorems of this section are taken out from (10).
439
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations
439
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations

8 Ferroelectrics
Theorem 4.1 The nearest approximation operator is 1-cut invariance.
Proof: It is a necessary condition for this approximation that
[T
m
(
˜
u
)]
1
=[
˜
u
]
1
.
Theorem 4.2 The nearest approximation operator is invariant to translations. i.e. for each
˜
u ∈F(R)
and a ∈ R,wehaveT
m
(
˜
u
+ a )=T
m
(
˜
u
)+a.
Proof: Let a be a real number. Then u
+ a = u + a and u + a = u + a. Therefore
val
(T
m
(
˜
u
+ a)) = val(
˜
u
+ a)=val(
˜
u
)+a = val(T
m
(
˜
u
)) + a,
amb
(T
m
(
˜
u
+ a)) = amb(
˜
u
+ a )=amb(
˜
u
)=amb(T
m
(
˜
u
)) = amb(T
m
(
˜
u
)+a),
Also for k
= 1,2,...,m −1, we have
val
k
((T
m
(
˜
u
)+a)) = val
k
((
˜
u
+ a )) = val
k
(
˜
u
)=val
k
(T
m
(
˜
u
)),
and
amb
k
((T
m
(
˜
u
)+a)) = amb
k
((
˜
u
+ a )) = amb
k
(
˜
u
)=amb
k
(T
m
(
˜
u
)).
Thus
D
m
(T
m
(
˜
u
+ a), T
m
(
˜
u
)+a)=0.
Since both T
m
(
˜
u
+ a) and T
m
(
˜
u
)+a have m-degree polynomial-form, then from Lemma 3.9
we have
T
m
(
˜
u
+ a )=T
m
(
˜
u
)+a.
Theorem 4.3 The nearest approximation operator is scale invariant. i.e. for each
˜
u ∈F(R) and
λ
∈ R,wehaveT
m
(λ
˜
u)=λT
m
(
˜
u
).
Proof: Let λ
= 0 be a real number. Thus for k = 0, 1, .. . ,m −1, we have
val
k
(λ
˜
u)=λval
k
(
˜
u
) , amb
k
(λ
˜
u)=λ amb
k
(
˜
u
).
and
D
m
(T
m
(λ
˜
u),λT
m
(
˜
u
)) = 0.
Therefore from Lemma 3.9 we have
T
m
(λ
˜
u)=λT
m
(
˜
u
).
Theorem 4.4 The nearest approximation operator fulfills the nearness criterion with respect to
m
−source metric D
m
defined in Definition 3.4, on the set of all m −degree polynomial-form fuzzy
numbers.
440
Ferroelectrics
440
Ferroelectrics

Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations 9
Proof: By Lemma 3.3, we have
D
m
(
˜
u, T
m
(
˜
u
)) = min
˜
v
∈PF
m
(R)
D
m
(
˜
u,
˜
v
),
therefore
D
m
(
˜
u, T
m
(
˜
u
)) ≤ D
m
(
˜
u,
˜
v
), ∀
˜
v
∈PF
m
(R).
Theorem 4.5 The nearest approximation operator is continuous.
Proof: An approximation operator T is continuous if for any
˜
u,
˜
v
∈F(R) we have
∀ > 0, ∃δ > 0, D
m
(
˜
u,
˜
v
) < δ =⇒ D
m
(T(
˜
u
), T(
˜
v
)) < .
Let D
m
(
˜
u,
˜
v
) < δ.ByTheorem3.2wehave
D
m
(T
m
(
˜
u
), T
m
(
˜
v
)) ≤ D
m
(T
m
(
˜
u
),
˜
u)+D
m
(
˜
u,
˜
v
)+D
m
(
˜
v, T
m
(
˜
v
))
and by Theorem 3.4 we have D
m
(T
m
(
˜
u
),
˜
u)=D
m
(
˜
v, T
m
(
˜
v
)) = 0. Thus
D
m
(T
m
(
˜
u
), T
m
(
˜
v
)) ≤ D
m
(
˜
u,
˜
v
) < δ.
Therefore its suffices to take δ
≤ .
Theorem 4.6 The nearest trapezoidal approximation operator (case m=1) is monotonic on any set of
fuzzy numbers with equal cores.
Proof: See (2).
Theorem 4.7 The nearest approximation operator is order invariant with respect to value function.
Proof: The proof is trivial, because val
(T
m
(
˜
u
)) = val(
˜
u
) and val(T
m
(
˜
v
)) = val(
˜
v
).
Theorem 4.8 The nearest approximation operator does not change the distance of fuzzy numbers by
m-source distance. i.e.
D
m
(T
m
(
˜
u
), T
m
(
˜
v
)) = T
m
(D
m
(
˜
u,
˜
v
)) = D
m
(
˜
u,
˜
v
).
Proof: The proof is trivial by Lemma 3.11.
By the following Theorem we show that the nearest approximation operator is a linear
operator:
Theorem 4.9 The nearest approximation operator is a linear operator on the set of all fuzzy numbers.
i.e. for a real number λ and two fuzzy numbers
˜
uand
˜
vwehave
T
m
(λ
˜
u +
˜
v
)=λT
m
(
˜
u
)+T
m
(
˜
v
).
441
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations
441
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations

10 Ferroelectrics
Proof: From Lemma 3.2 we have
D
m
(λ
˜
u +
˜
v, λT
m
(
˜
u
)+T
m
(
˜
v
)) ≤ D
m
(λ
˜
u, λT
m
(
˜
u
)) + D
m
(
˜
v, T
m
(
˜
v
))
=
D
m
(λ
˜
u, λT
m
(
˜
u
))
= |
λ|D
m
(
˜
u, T
m
(
˜
u
)) = 0.
Also we have
D
m
(λ
˜
u +
˜
v, T
m
(λ
˜
u +
˜
v
)) = 0,
therefore
D
m
(T
m
(λ
˜
u +
˜
v
), λT
m
(
˜
u
)+T
m
(
˜
v
)) = 0.
Since both fuzzy numbers T
m
(λ
˜
u +
˜
v
) and λT
m
(
˜
u
)+T
m
(
˜
v
) belong to PF
m
(R),wehave
T
m
(λ
˜
u +
˜
v
)=λT
m
(
˜
u
)+T
m
(
˜
v
).
5. Linear system of fuzzy equations
In this section we introduce a method for solving fuzzy linear system of equations, and this
method is taken from (9).
Let
˜
A and
˜
b be a matrix and a vector with fuzzy number arrays, respectively. A system of
fuzzy linear equations with crisp variables is a system with the following form:
˜
Ax
=
˜
b.(5.1)
Equivalently we have
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
˜
a
11
x
1
+
˜
a
12
x
2
+ ...+
˜
a
1n
x
n
=
˜
b
1
˜
a
21
x
1
+
˜
a
22
x
2
+ ...+
˜
a
2n
x
n
=
˜
b
2
.
.
.
˜
a
n1
x
1
+
˜
a
n2
x
2
+ ...+
˜
a
nn
x
n
=
˜
b
n
(5.2)
where fori, j
= 1, ···,n;
˜
a
ij
’s and
˜
b
i
’s are fuzzy numbers.
Lemma 5.1
Consider two systems of linear equations as follows
˜
Ax
=
˜
b.(5.3)
and
[
˜
A
]
1
x =[
˜
b
]
1
.(5.4)
If system (5.3) has a solution then the system (5.4) has a solution. Furthermore if x
∗
be the
solution of (5.3) then x
∗
is the solution of (5.4) too.
Proof: It is straightforward.
Corollary 5.2 If system (5.4) hasn’t any solution then the system (5.3) hasn’t any solution too.
442
Ferroelectrics
442
Ferroelectrics
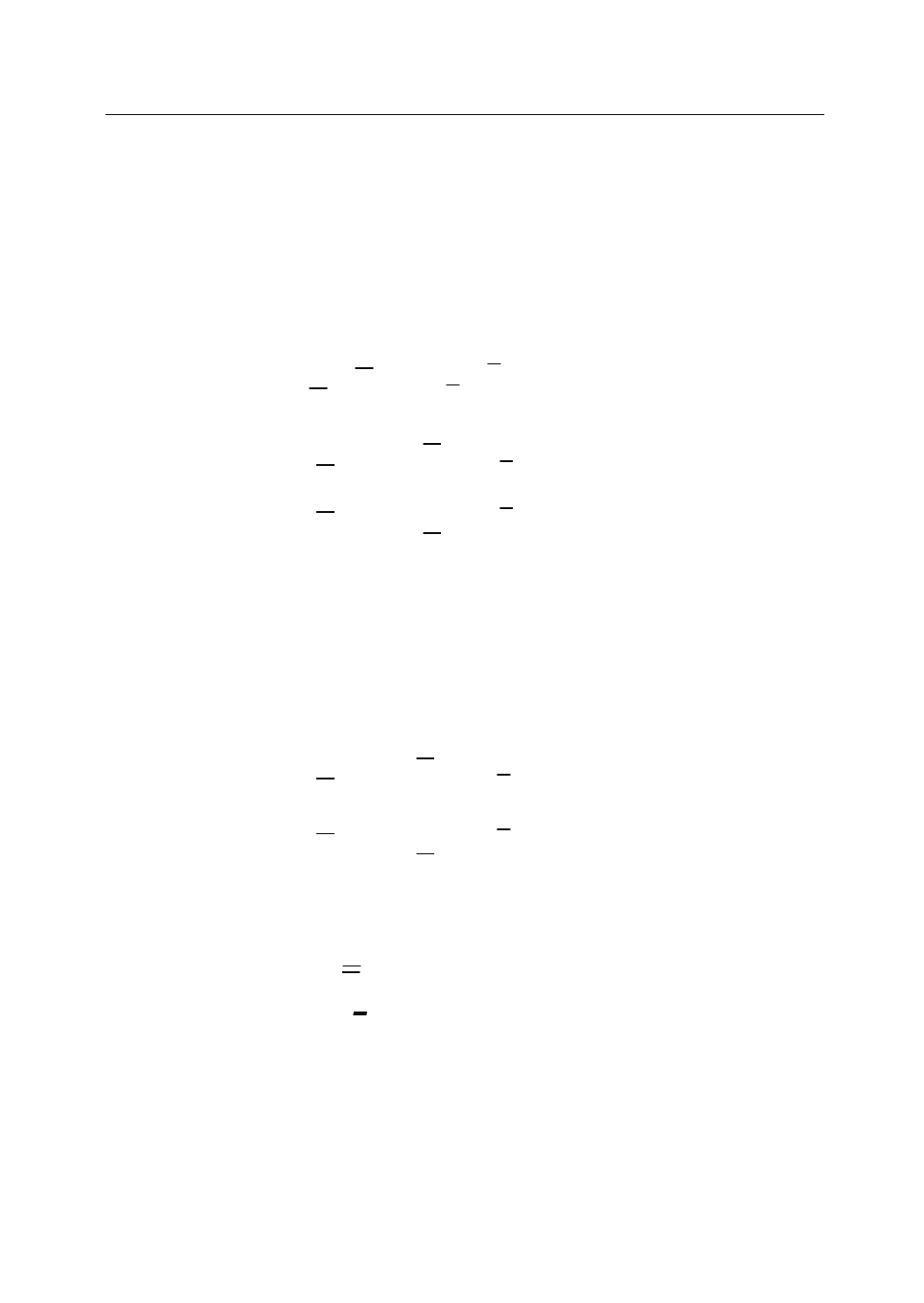
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations 11
6. Solution of fuzzy linear equations
In this Section we try to solve a system of fuzzy linear equations with m−degree
polynomial-form fuzzy number coefficients. Let for positive integer m,all
˜
a
ij
’s and
˜
b
i
’s are
fuzzy numbers with m
−degree polynomial-form, for i, j = 1, ···,n. Our equations now are as
follows:
n
∑
j=1
˜
a
ij
x
j
=
˜
b
i
, i = 1,...,n.(6.1)
where for i, j
= 1,...,n;
˜
a
ij
,
˜
b
i
∈PF
m
(R) ,andx
j
∈ R.Wecanconsider(6.1)as
n
∑
j=1
(a
ij
(r), a
ij
(r)) x
j
=(b
i
(r),b
i
(r)) , i = 1,...,n.
It means that
∑
x
j
≥0
a
ij
(r)x
j
+
∑
x
j
<0
a
ij
(r)x
j
= b
i
(r), i = 1,...,n,(6.2)
and
∑
x
j
≥0
a
ij
(r)x
j
+
∑
x
j
<0
a
ij
(r)x
j
= b
i
(r), i = 1,...,n.(6.3)
Let x
j
= x
j
− x
j
,where
x
j
=
x
j
, x
j
≥ 0,
0, x
j
< 0,
and
x
j
=
0, x
j
≥ 0,
−x
j
, x
j
< 0,
thus x
j
, x
j
≥ 0, and we have
n
∑
j=1
a
ij
(r)x
j
−
n
∑
j=1
a
ij
(r)x
j
= b
i
(r), i = 1,...,n,(6.4)
and
n
∑
j=1
a
ij
(r)x
j
−
n
∑
j=1
a
ij
(r)x
j
= b
i
(r), i = 1,...,n.(6.5)
Since
˜
a
ij
’s and
˜
b
i
’s are fuzzy numbers with m−degree polynomial-form, there exist coefficients
c
ijk
, d
ijk
, e
ik
and f
ik
such that
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
a
ij
(r)=
∑
m
k
=0
c
ijk
r
k
, i, j = 1,...,n,
a
ij
(r)=
∑
m
k
=0
d
ijk
r
k
, i, j = 1,...,n,
b
i
(r)=
∑
m
k
=0
e
ik
r
k
, i = 1,...,n,
b
i
(r)=
∑
m
k
=0
f
ik
r
k
, i = 1,...,n.
(6.6)
By substituting (6.6) into the equations (6.4) and (6.5), we have
n
∑
j=1
m
∑
k=0
c
ijk
r
k
x
j
−
n
∑
j=1
m
∑
k=0
d
ijk
r
k
x
j
=
m
∑
k=0
e
ik
r
k
, i = 1,...,n,
443
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations
443
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations

12 Ferroelectrics
and
n
∑
j=1
m
∑
k=0
d
ijk
r
k
x
j
−
n
∑
j=1
m
∑
k=0
c
ijk
r
k
x
j
=
m
∑
k=0
f
ik
r
k
, i = 1,...,n.
Consequently for all i
= 1,2,...,n,andk = 0,1,...,m,wehave
n
∑
j=1
c
ijk
x
j
−
n
∑
j=1
d
ijk
x
j
= e
ik
,(6.7)
and
n
∑
j=1
d
ijk
x
j
−
n
∑
j=1
c
ijk
x
j
= f
ik
.(6.8)
Considering
C
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
c
110
... c
1n0
.
.
.
.
.
.
c
11m
... c
1nm
.
.
.
.
.
.
c
n10
... c
nn0
.
.
.
.
.
.
c
n1m
... c
nnm
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
, D
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
d
110
... d
1n0
.
.
.
.
.
.
d
11m
... d
1nm
.
.
.
.
.
.
d
n10
... d
nn0
.
.
.
.
.
.
d
n1m
... d
nnm
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
and
e
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
e
10
.
.
.
e
1m
.
.
.
e
n0
.
.
.
e
nm
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
, f
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
f
10
.
.
.
f
1m
.
.
.
f
n0
.
.
.
f
nm
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
, x
=
⎛
⎜
⎝
x
1
.
.
.
x
n
⎞
⎟
⎠
, x
=
⎛
⎜
⎝
x
1
.
.
.
x
n
⎞
⎟
⎠
, y
=
x
x
one should solve the following system of linear equations,
Sy
= d,(6.9)
where
S
=
C
−D
D
−C
, x
=
x
x
, d
=
e
f
and we have x
= x
−x
.
S is a 2n
(m + 1) × 2n matrix, and since m > 0, we try to solve the following least squares
problem:
min
y∈R
2n
Sy −d
2
. (6.10)
444
Ferroelectrics
444
Ferroelectrics

Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations 13
It is well known that the solution of (6.10) is equal to the solution of its corresponding normal
system of equations as follows:
S
T
Sy = S
T
d. (6.11)
Lemma 6.1
The system (6.11) always has a solution even when S
T
S is singular.
Proof: See (23).
Let x
∗
and x be the solution of systems (5.3) and (5.4), respectively and let ˜x and x be the
obtained solutions corresponding to the systems (6.9) and (6.11), respectively. From the last
lemma it is known that x always exists.
Lemma 6.2
Let all
˜
a
ij
’s and
˜
b
i
’s have m−degree polynomial-form. If x
∗
exists then x and ˜x exist and
x
∗
= x = ˜x = x.
Proof: It is straightforward.
x is the least squares solution of the system
˜
Ax =
˜
b, also if it’s corresponding vector y satisfies
in the system Sy
= d then x is the exact solution of the system
˜
Ax =
˜
b.
If S
T
S is nonsingular then the solutions of two systems (6.9) and (6.11) are the same and y
∗
=
(
S
T
S)
−1
S
T
d.
By a simple computations it can be shown that
S
T
S =
L
−M
−ML
,
where
L
= C
T
C + D
T
D , M = C
T
D + D
T
C.
Thus
S
T
S −→
L
− M L −M
−ML
−→
L
−M 0
−ML+ M
,
therefore
|S
T
S| = |L −M|·|L + M|.
Also we have
L
−M =(C −D)
T
(C −D) , L + M =(C + D)
T
(C + D).
If C
−D be a full rank matrix then L − M is nonsingular and if C + D be a full rank matrix
then L
+ M is nonsingular. i.e. if rank(C ±D)=n then S
T
S is nonsingular.
7. Numerical solution of fuzzy linear equations
In this section we consider a system of fuzzy linear equations as
˜
Ax
=
˜
b,(7.1)
where for i, j
= 1, ···,n;
˜
a
ij
’s and
˜
b
i
’s, are from LR type fuzzy numbers.
445
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations
445
Numerical Solution of a System of Polynomial Parametric form Fuzzy Linear Equations

14 Ferroelectrics
For the purpose of solving (7.1), we consider the following system of equations
˜
A
(m)
x =
˜
b
(m)
,(7.2)
where for i, j
= 1, ···,n; the quantities
˜
a
(m)
ij
’s and
˜
b
(m)
i
’s are the nearest approximations of
the given numbers
˜
a
ij
’s and
˜
b
i
’s out of PF
m
(R), respectively. Existence of the nearest
approximations of the given fuzzy numbers is known from Lemma 3.6.
From Lemma 6.1 we know that this system has a least squares solution. Using the process in
the Section 6 we obtain a least squares solution x
(m)
for this system. We name this solution,
the m
-degree nearest least squares
(m−DNLS) solution of the system (5.3). Thus we have
˜
A
(m)
x
(m)
=
˜
b
(m)
,(7.3)
Choosing m depends on the shape of left and right spread functions L and R,andthe
derivation order of them.
8. Numerical examples
In this Section we present some numerical examples which have been solved on both
m
−degree polynomial-form fuzzy number coefficients and general LR fuzzy number
coefficients.
Example 8.1 Consider the following 2 by 2 system of equations with m
= 1:
(−1 + 2r,4−2r)x
1
+(−2 + 3r,3−2r)x
2
=(−8 + 13r,17−10r),
(1 + r,4−r)x
1
+(2r,5−2r)x
2
=(2 + 8r,23−8r),
For this system of equations by solving the least squares system we have x
1
= 2andx
2
= 3.
Example 8.2 Consider the following 2 by 2 system of equations with m
= 1:
(−1 + r,3−r)x
1
+(1 + 2r,4−r)x
2
=(−12 + 11r,17−8r),
(−1 + 2r,3−2r)x
1
+(3r,6−2r)x
2
=(−15 + 19r,23 −16r),
For this system of equations by solving the least squares system we have x
1
= −5andx
2
= 3.
Example 8.3 Consider the following 2 b y 2 system of equations with m
= 2:
˜
a
11
x
1
+
˜
a
12
x
2
=
˜
b
1
,
˜
a
21
x
1
+
˜
a
22
x
2
=
˜
b
2
,
where
˜
a
11
=(3r + r
2
,7−3r + 2r
2
)
˜
a
12
=(2r + r
2
,4−2r + 2r
2
)
˜
a
21
=(1 + 2r + r
2
,8−3r + r
2
)
˜
a
22
=(1 + 2r + r
2
,6−3r + 2r
2
)
˜
b
1
=(48.45r + 17.1r
2
,111.15 −48.45r + 34.2r
2
)
˜
b
2
=(17.1 + 34.2r + 17.1r
2
,131.1 −51.3r + 19.95r
2
),
For this system of equations by solving the least squares system we have x
1
= 14.85 and x
2
=
2.25.
446
Ferroelectrics
446
Ferroelectrics
