Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


We ®rst write
rV
^
e
1
^
e
2
^
e
3
@
@x
1
@
@x
2
@
@x
3
V
1
V
2
V
3
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
;
then notice that
@
@x
1
V
2
@V
2
@x
1
@
@x
1
V
2
;
so we can expand the determinant in the above equation as a sum of two deter-
minants:
rV
^
e
1
^
e
2
^
e
3
@
@x
1
@
@x
2
@
@x
3
V
1
V
2
V
3
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
^
e
1
^
e
2
^
e
3
@
@x
1
@
@x
2
@
@x
3
V
1
V
2
V
3
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
r VrV:
Alternatively, we can simplify the proof with the help of the permutation symbols
"
ijk
:
rV
X
i; j;k
"
ijk
^
e
i
@
@x
j
V
k
X
i; j;k
"
ijk
^
e
i
@V
k
@x
j
X
i; j;k
"
ijk
^
e
i
@
@x
j
V
k
r VrV:
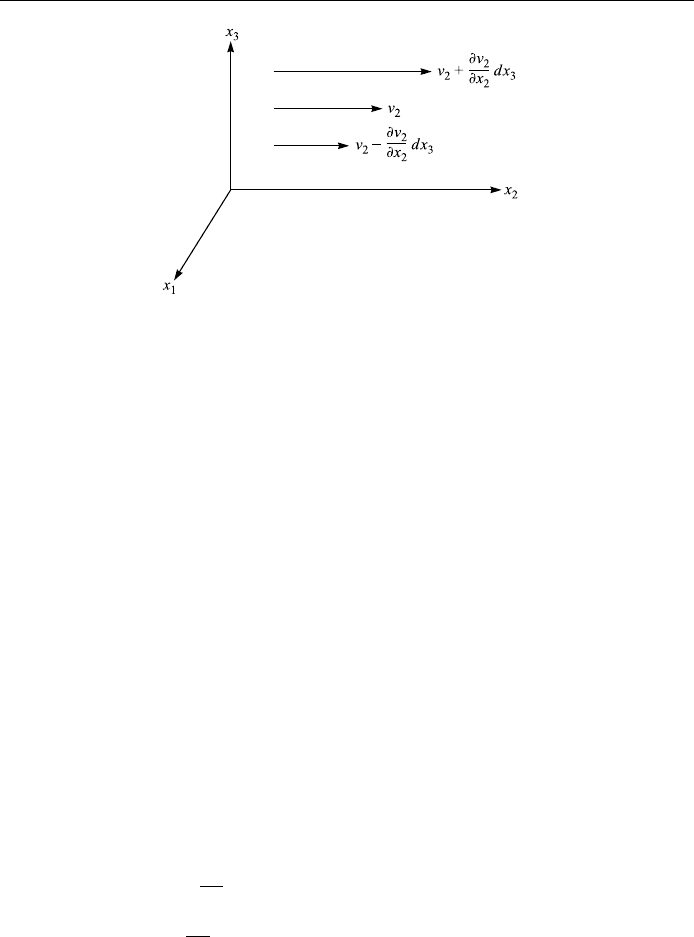
A vector ®eld that has non-vanishing curl is called a vortex ®eld, and the curl of
the ®eld vector is a measure of the vorticity of the vector ®eld.
The physical signi®cance of the curl of a vector is not quite as transparent as
that of the divergence. The following examp le from ¯uid ¯ow will help us to
develop a better feeling. Fig. 1.15 shows that as the component v
2
of the velocity
v of the ¯uid increases with x
3
, the ¯uid curls about the x
1
-axis in a negative sense
(rule of the right-hand screw), where @v
2
=@x
3
is considered positive. Similarly, a
positive curling about the x
1
-axis would result from v
3
if @v
3
=@x
2
were positive.
Therefore, the total x
1
component of the curl of v is
curl v
1
@v
3
=@x
2
ÿ @v
2
=@x
3
;
which is the same as the x
1
component of Eq. (1.50).
26
VECTOR AND TENSOR ANALYSIS
Formulas involving r
We now list some important formulas involving the vector diÿerential operator r,
some of which are recapitulation. In these formulas, A and B are diÿerentiable
vector ®eld functio ns, and f and g are diÿerentiable scalar ®eld functions of
position x
1
; x
2
; x
3
:
(1) rfgf rg grf ;
(2) rf Af rA rf A;
(3) rf Af rA rf A;
(4) rrf 0;
(5) rrA0;
(6) rA B r AB ÿrBA;
(7) rA BB rA ÿ Br AAr BÿA rB;
(8) r r A rr Aÿr
2
A;
(9) rA BA rBB rAA rB B rA;
(10) A rr A;
(11) rr 3;
(12) rr 0;
(13) rr
ÿ3
r0;
(14) dF dr rF
@F
@t
dt F a diÿerentiable vector ®eld quantity);
(15) d' dr r'
@'
@t
dt (' a diÿ erentiable scalar ®eld quantity).
Orthogonal cu rvilinear coordinates
Up to this point all calculations have been performed in rectangular Cartesian
coordinates. Many calculations in physics can be greatly simpli®ed by using,
instead of the familiar rectangular Cartesian coordinate system, another kind of
27
FORMULAS INVOLVING r
Figure 1.15. Curl of a ¯uid ¯ow.
system which takes advantage of the relations of symm etry involved in the parti-
cular problem under consideration. For example, if we are dealing with sphere, we
will ®nd it expedient to describe the position of a point in sphere by the spherical
coordinates (r;;. Spherical coordinates are a special case of the orthogonal
curvilinear coordinate system. Let us now proceed to discuss these more general
coordinate systems in order to obtain expressions for the gradient, divergence,
curl, and Laplacian. Let the new coordinates u
1
; u
2
; u
3
be de®ned by specifying the
Cartesian coordinates (x
1
; x
2
; x
3
) as functions of (u
1
; u
2
; u
3
:
x
1
f u
1
; u
2
; u
3
; x
2
gu
1
; u
2
; u
3
; x
3
hu
1
; u
2
; u
3
; 1:54
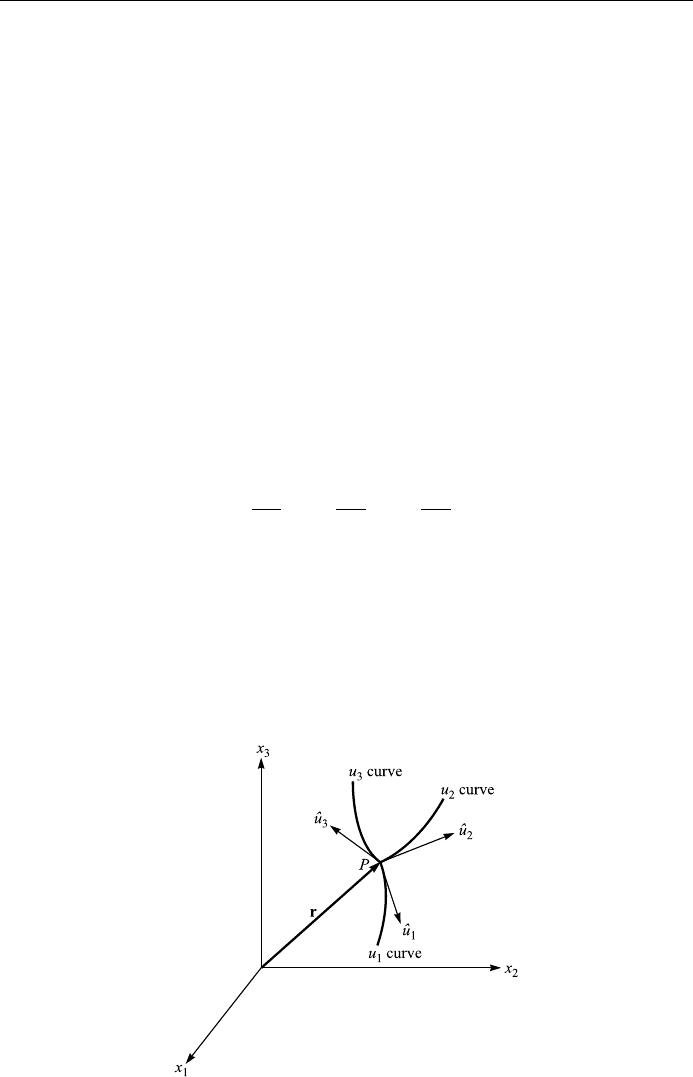
where f, g, h are assumed to be continuou s, diÿerentiable. A point P (Fig. 1.16) in
space can then be de®ned not only by the rectangular coordinates (x
1
; x
2
; x
3
) but
also by curvilinear coordinates (u
1
; u
2
; u
3
).
If u
2
and u
3
are constant as u
1
varies, P (or its position vector r) describes a curve
which we call the u
1
coordinate c urve. Similarly, we can de®ne the u
2
and u
3
coordi-
nate curves through P. W e adopt the convention that the new coordinate system is a
right handed system, like the old one. In the new system dr takes the form:
dr
@r
@u
1
du
1
@r
@u
2
du
2
@r
@u
3
du
3
:
The vector @r=@u
1
is tangent to the u
1
coordinate curve at P.If
^
u
1
is a unit vector
at P in this direction, then
^
u
1
@r=@u
1
=j@r=@u
1
j, so we can write @r=@u
1
h
1
^
u
1
,
where h
1
j@r=@u
1
j. Similarly we can write @r=@u
2
h
2
^
u
2
and @r=@u
3
h
3
^
u
3
,
where h
2
j@r=@u
2
j and h
3
j@r=@u
3
j, respectively. Then dr can be written
dr h
1
du
1
^
u
1
h
2
du
2
^
u
2
h
3
du
3
^
u
3
: 1:55
28
VECTOR AND TENSOR ANALYSIS
Figure 1.16. Curvilinear coordinates.

The quantities h
1
; h
2
; h
3
are sometimes called scale factors. The unit vectors
^
u
1
,
^
u
2
,
^
u
3
are in the direction of increasing u
1
; u
2
; u
3
, respectively.
If
^
u
1
,
^
u
2
,
^
u
3
are mutually perpendicular at any point P, the curvilinear coordi-
nates are called orthogonal. In such a case the element of arc length ds is given by
ds
2
dr dr h
2
1
du
2
1
h
2
2
du
2
2
h
2
3
du
2
3
: 1:56
Along a u
1
curve, u
2
and u
3
are constants so that dr h
1
du
1
^
u
1
. Then the
diÿerential of arc length ds
1
along u
1
at P is h
1
du
1
. Similarly the diÿerential arc
lengths along u
2
and u
3
at P are ds
2
h
2
du
2
, ds
3
h
3
du
3
respectively.
The volume of the parallelepiped is given by
dV jh
1
du
1
^
u
1
h
2
du
2
^
u
2
h
3
du
3
^
u
3
j h
1
h
2
h
3
du
1
du
2
du
3
since j
^
u
1
^
u
2
^
u
3
j1. Alternativel y dV can be writt en as
dV
@r
@u
1
@r
@u
2
@r
@u
3
þ
þ
þ
þ
þ
þ
þ
þ
du
1
du
2
du
3
@x
1
; x
2
; x
3
@u
1
; u
2
; u
3
þ
þ
þ
þ
þ
þ
þ
þ
du
1
du
2
du
3
; 1:57
where
J
@x
1
; x
2
; x
3
@u
1
; u
2
; u
3
@x
1
@u
1
@x
1
@u
2
@x
1
@u
3
@x
2
@u
1
@x
2
@u
2
@x
2
@u
3
@x
3
@u
1
@x
3
@u
2
@x
3
@u
3
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
is called the Jacob ian of the transformation.
We assume that the Jacobian J 6 0 so that the transformation (1.54) is one to
one in the neighborhood of a point.
We are now ready to express the gradient, divergence, and curl in terms of
u
1
; u
2
,andu
3
.If is a scalar function of u
1
; u
2
,andu
3
, then the gradient takes the
form
r grad
1
h
1
@
@u
1
^
u
1
1
h
2
@
@u
2
^
u
2
1
h
3
@
@u
3
^
u
3
: 1:58
To derive this, let
r f
1
^
u
1
f
2
^
u
2
f
3
^
u
3
; 1:59
where f
1
; f
2
; f
3
are to be determined. Since
dr
@r
@u
1
du
1
@r
@u
2
du
2
@r
@u
3
du
3
h
1
du
1
^
u
1
h
2
du
2
^
u
2
h
3
du
3
^
u
3
;
29
ORTHOGONAL CURVILINEAR COORDINATES

we have
d r dr h
1
f
1
du
1
h
2
f
2
du
2
h
3
f
3
du
3
:
But
d
@
@u
1
du
1
@
@u
2
du
2
@
@u
3
du
3
;
and on equating the two equations, we ®nd
f
i
1
h
i
@
@u
i
; i 1; 2; 3:
Substituting these into Eq. (1.57), we obtain the result Eq. (1.58).
From Eq. (1.58) we see that the operator r takes the form
r
^
u
1
h
1
@
@u
1
^
u
2
h
2
@
@u
2
^
u
3
h
3
@
@u
3
: 1:60
Because we will need them later, we now proceed to prove the following two
relations:
(a) jru
i
jh
ÿ1
i
; i 1, 2, 3.
(b)
^
u
1
h
2
h
3
ru
2
ru
3
with similar equations for
^
u
2
and
^
u
3
. (1.61)
Proof: (a) Let u
1
in Eq. (1.51), we then obtain ru
1
^
u
1
=h
1
and so
jru
1
jj
^
u
1
jh
ÿ1
1
h
ÿ1
1
; since j
^
u
1
j1:
Similarly by letting u
2
and u
3
, we obtain the relations for i 2 and 3.
(b) From (a) we have
ru
1
^
u
1
=h
1
; ru
2
^
u
2
=h
2
; and ru
3
^
u
3
=h
3
:
Then
ru
2
ru
3
^
u
2
^
u
3
h
2
h
3
^
u
1
h
2
h
3
and
^
u
1
h
2
h
3
ru
2
ru
3
:
Similarly
^
u
2
h
3
h
1
ru
3
ru
1
and
^
u
3
h
1
h
2
ru
1
ru
2
:
We are now ready to express the divergence in terms of curvilinear coordinates.
If A A
1
^
u
1
A
2
^
u
2
A
3
^
u
3
is a vector function of orthogonal curvilinear coordi-
nates u
1
, u
2
, and u
3
, the divergence will take the form
rA div A
1
h
1
h
2
h
3
@
@u
1
h
2
h
3
A
1
@
@u
2
h
3
h
1
A
2
@
@u
3
h
1
h
2
A
3
: 1:62
To derive (1.62), we ®rst write rA as
rA rA
1
^
u
1
rA
2
^
u
2
rA
3
^
u
3
; 1:63
30
VECTOR AND TENSOR ANALYSIS

then, because
^
u
1
h
1
h
2
ru
2
ru
3
, we express rA
1
^
u
1
)as
rA
1
^
u
1
rA
1
h
2
h
3
ru
2
ru
3
^
u
1
h
2
h
3
ru
2
ru
3
rA
1
h
2
h
3
ru
2
ru
3
A
1
h
2
h
3
rru
2
ru
3
;
where in the last step we have used the vector identity: rA
rA r A .Nowru
i
^
u
i
=h
i
; i 1, 2, 3, so rA
1
^
u
1
) can be rewritten
as
rA
1
^
u
1
rA
1
h
2
h
3
^
u
2
h
2
^
u
3
h
3
0 rA
1
h
2
h
3
^
u
1
h
2
h
3
:
The gradient rA
1
h
2
h
3
is given by Eq. (1.58), and we have
rA
1
^
u
1
^
u
1
h
1
@
@u
1
A
1
h
2
h
3
^
u
2
h
2
@
@u
2
A
1
h
2
h
3
^
u
3
h
3
@
@u
3
A
1
h
2
h
3
^
u
1
h
2
h
3
1
h
1
h
2
h
3
@
@u
1
A
1
h
2
h
3
:
Similarly, we have
rA
2
^
u
2
1
h
1
h
2
h
3
@
@u
2
A
2
h
3
h
1
; and rA
3
^
u
3
1
h
1
h
2
h
3
@
@u
3
A
3
h
2
h
1
:
Substituting these into Eq. (1.63), we obtain the result, Eq. (1.62).
In the same manner we can derive a formula for curl A . We ®rst write it as
rA rA
1
^
u
1
A
2
^
u
2
A
3
^
u
3
and then evaluate rA
i
^
u
i
.
Now
^
u
i
h
i
ru
i
; i 1, 2, 3, and we express rA
1
^
u
1
as
rA
1
^
u
1
rA
1
h
1
ru
1
rA
1
h
1
ru
1
A
1
h
1
rru
1
rA
1
h
1
^
u
1
h
1
0
^
u
1
h
1
@
@u
1
A
1
h
1
^
u
2
h
2
@
@u
2
A
2
h
2
^
u
3
h
3
@
@u
3
A
3
h
3
^
u
1
h
1
^
u
2
h
3
h
1
@
@u
3
A
1
h
1
ÿ
^
u
3
h
1
h
2
@
@u
2
A
1
h
1
;
31
ORTHOGONAL CURVILINEAR COORDINATES

with similar expressions for rA
2
^
u
2
and rA
3
^
u
3
. Adding these together,
we get rA in orthogonal curvilinear coordinates:
rA
^
u
1
h
2
h
3
@
@u
2
A
3
h
3
ÿ
@
@u
3
A
2
h
2
^
u
2
h
3
h
1
@
@u
3
A
1
h
1
ÿ
@
@u
1
A
3
h
3
^
u
3
h
1
h
2
@
@u
1
A
2
h
2
ÿ
@
@u
2
A
1
h
1
: 1:64
This can be written in determinant form:
rA
1
h
1
h
2
h
3
h
1
^
u
1
h
2
^
u
2
h
3
^
u
3
@
@u
1
@
@u
2
@
@u
3
A
1
h
1
A
2
h
2
A
3
h
3
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
: 1:65
We now express the Laplacian in orthogonal curvilinear coordinates. From
Eqs. (1.58) and (1.62) we have
r grad
1
h
1
@
@u
1
^
u
1
1
h
2
@
@u
2
^
u
1
h
3
@
@u
3
^
u
3
;
rA div A
1
h
1
h
2
h
3
@
@u
1
h
2
h
3
A
1
@
@u
2
h
3
h
1
A
2
@
@u
3
h
1
h
2
A
3
:
If A r, then A
i
1=h
i
@=@u
i
, i 1, 2, 3; and
rA rr r
2
1
h
1
h
2
h
3
@
@u
1
h
2
h
3
h
1
@
@u
1
@
@u
2
h
3
h
1
h
2
@
@u
2
@
@u
3
h
1
h
2
h
3
@
@u
3
: 1:66
Special orthogonal coordinate systems
There are at least nine special orthogonal coordinates systems, the most common
and useful ones are the cylindrical and spherical coordinates; we introduce these
two coordinat es in this section.
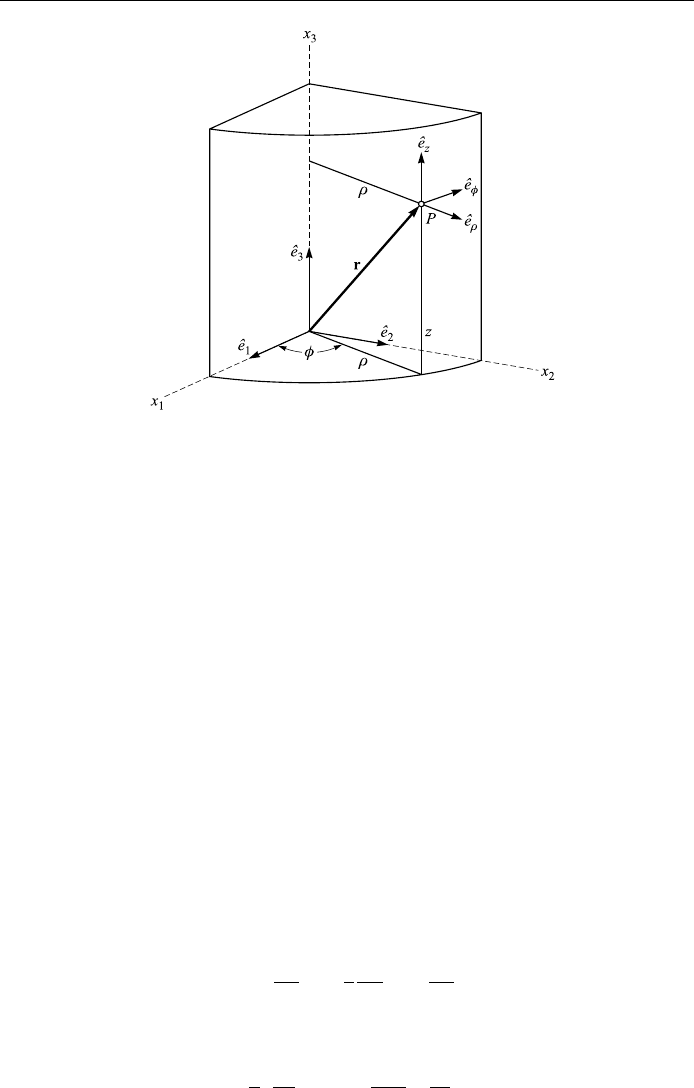
Cylindrical coordinates ; ; z
u
1
; u
2
; u
3
z; and
^
u
1
e
;
^
u
2
e
^
u
3
e
z
:
From Fig. 1.17 we see that
x
1
cos ; x
2
sin ; x
3
z
32
VECTOR AND TENSOR ANALYSIS
where
0; 0 2; ÿ1 < z < 1:
The square of the element of arc length is given by
ds
2
h
2
1
d
2
h
2
2
d
2
h
2
3
dz
2
:
To ®nd the scale factors h
i
, we notice that ds
2
dr dr where
r cos e
1
sin e
2
ze
3
:
Thus
ds
2
dr dr d
2
2
d
2
dz
2
:
Equating the two ds
2
, we ®nd the scale factors:
h
1
h
1; h
2
h
; h
3
h
z
1: 1:67
From Eqs. (1.58), (1.62), (1.64), and (1.66) we ®nd the gradient, divergence, curl,
and Laplacian in cylindrical coordinates:
r
@
@
e
1
@
@
e
@
@z
e
z
; 1:68
where ; ; z is a scalar function;
rA
1
@
@
A
@A
@
@
@z
A
z
; 1:69
33
SPECIAL ORTHOGONAL COORDINATE SYSTEMS
Figure 1.17. Cylindrical coordinates.
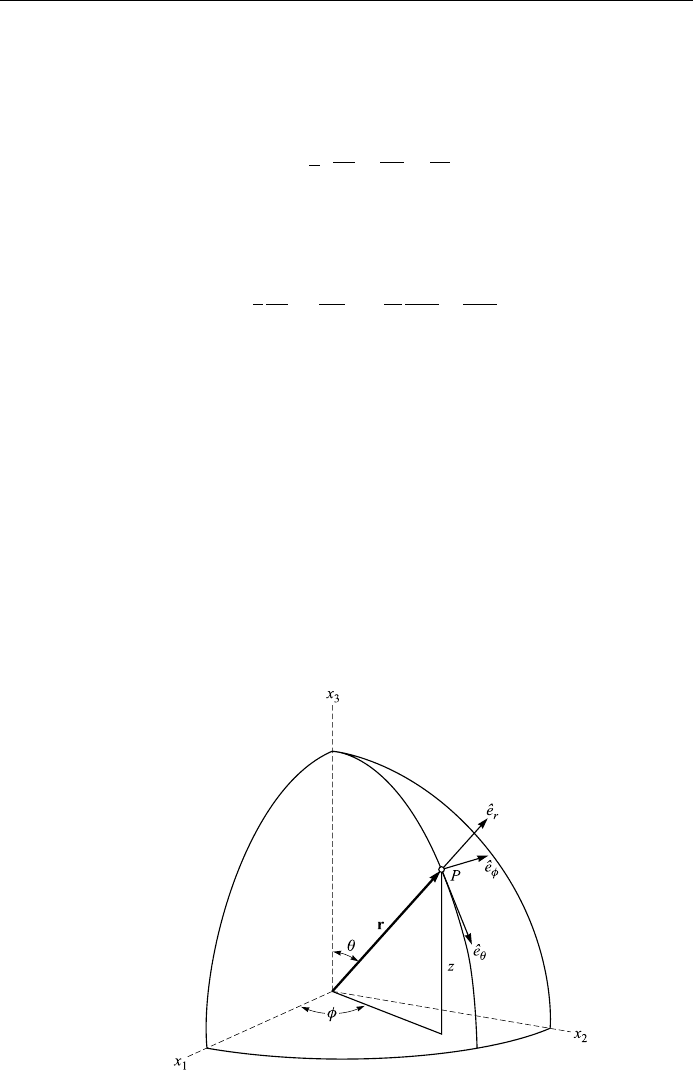
where
A A
e
A
e
A
z
e
z
;
rA
1
e
e
e
z
@
@
@
@
@
@z
A
A
A
z
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
; 1:70
and
r
2
1
@
@
@
@
1
2
@
2
@
2
@
2
@z
2
: 1:71
Spherical coordinates r;;
u
1
r; u
2
; u
3
;
^
u
1
e
r
;
^
u
2
e
;
^
u
3
e
From Fig. 1.18 we see that
x
1
r sin cos ; x
2
r sin sin ; x
3
r cos :
Now
ds
2
h
2
1
dr
2
h
2
2
d
2
h
2
3
d
2
but
r r sin cos
^
e
1
r sin sin
^
e
2
r cos
^
e
3
;
34
VECTOR AND TENSOR ANALYSIS
Figure 1.18. Spherical coordinates.

so
ds
2
dr dr dr
2
r
2
d
2
r
2
sin
2
d
2
:
Equating the two ds
2
, we ®nd the scale factors: h
1
h
r
1, h
2
h
r,
h
3
h
r sin . We then ®nd, from Eqs. (1.58), (1.62), (1.64), and (1.66), the
gradient, divergence, curl, and the Laplacian in spherical coordinates:
r
^
e
r
@
@r
^
e
1
r
@
@
^
e
1
r sin
@
@
; 1:72
rA
1
r
2
sin
sin
@
@r
r
2
A
r
r
@
@
sin A
r
@A
@
; 1:73
rA
1
r
2
sin
^
e
r
r
^
e
r sin
^
e
@
@r
@
@
@
@
A
r
rA
r
r sin A
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
; 1:74
r
2
1
r
2
sin
sin
@
@r
r
2
@
@r
@
@
sin
@
@
1
sin
@
2
@
2
"#
: 1:75
Vector integration and integral theorems
Having discussed vector diÿerentiation, we now turn to a discussion of vector
integration. After de®ning the concepts of line, surface, and volume integrals of
vector ®elds, we then proceed to the important integral theorems of Gauss,
Stokes, and Green.
The integration of a vector, which is a function of a single scalar u, can proceed
as ordinary scalar integration. Given a vector
AuA
1
u
^
e
1
A
2
u
^
e
2
A
3
u
^
e
3
;
then
Z
Audu
^
e
1
Z
A
1
udu
^
e
2
Z
A
2
udu
^
e
3
Z
A
3
udu B;
where B is a constant of integration, a constant vector. Now consider the integral
of the scalar product of a vector Ax
1
; x
2
; x
3
) and dr between the limit
P
1
x
1
; x
2
; x
3
) and P
2
x
1
; x
2
; x
3
:
35
VECTOR INTEGRATION AND INTEGRAL THEOREMS
