Чорней Р.К. Теорія автоматів
Подождите немного. Документ загружается.

Дискретна математика
Руслан Чорней

Роздiл 1
Теорiя автоматiв
1.1. Поняття скiнченного автомата. Методи задання
автоматiв
Скiнченним автоматом (у подальшому просто автоматом або СА) називає-
ться система A = (X, Y, U, δ, λ), в якiй X = {x
1
, x
2
, ..., x
m
} i Y = {y
1
, y
2
, ..., y
n
} —
скiнченнi множини (алфавiти) вiдповiдно вхiдних i вихiдних сигналiв,
U = {a
1
, a
2
, ..., a
s
} — множина внутрiшнiх станiв автомата. Функцiї δ i λ опи-
сують алгоритм функцiонування (поведiнку) автомата A. Функцiя δ : U × X → U
називається функцiєю переходiв, а функцiя λ : U × X → Y — функцiєю виходiв
автомата A.
Пiдкреслимо одну особливу властивiсть моделi СА, яка випливає з подальшої фi-
зичної iнтерпретацiї цiєї моделi. Вважатимемо, що автомат A функцiонує в дискре-
тному часi, тобто час функцiонування автомата розбивається на вiдрiзки однакової
довжини — такти. Межi тактiв t називають моментами абстрактного дискретного
автоматного часу i нумерують цiлими числами, починаючи з нуля. Вважатиме-
мо, що значення вхiдних i вихiдних сигналiв та значення станiв автомата можуть
змiнюватися тiльки в моменти автоматного часу t = 0, 1, 2, ...
Якщо позначимо як x(t) ∈ X, y(t) ∈ Y , a(t) ∈ U значення вiдповiдно вхiдно-
го i вихiдного сигналiв та стану автомата в момент автоматного часу t, то робота
автомата A описується такими спiввiдношеннями:
a(t + 1) = δ
¡
a(t), x(t)
¢
, y(t + 1) = λ
¡
a(t), x(t)
¢
. (1.1)
Цi спiввiдношення називаються канонiчними рiвняннями автомата A.
Перше з канонiчних рiвнянь можна прочитати так: стан автомата A у будь-який
момент автоматного часу t + 1 однозначно визначається сигналом, що подається на
вхiд автомата, i станом автомата A в попереднiй момент автоматного часу. При цьому
кажуть, що автомат A переходить зi стану a(t) у стан a(t + 1).
Крiм змiни станiв результатом роботи автомата є також видача вихiдних сигналiв
за законом, який визначається другим канонiчним рiвнянням автомата.
2

1.1. Поняття скiнченного автомата. Методи задання автоматiв
Якщо в автоматi A видiлено стан, у якому автомат A перебуває в момент авто-
матного часу t = 0, то цей стан називають початковим (як правило, початковим
станом вважають a
0
), а автомат A називають iнiцiальним i позначають A/a
0
. В
усiх наступних спiввiдношеннях не вказуватимемо явно залежнiсть змiнних та ре-
зультатiв функцiй переходiв i виходiв вiд автоматного часу t, крiм випадкiв, коли це
необхiдно.
Для розв’язання рiзних задач теорiї автоматiв зручно використовувати рiзнi
способи (методи) задання автоматiв. Опишемо три найпоширенiшi з них. Усi
три методи iстотно використовують той факт, що функцiї δ i λ автомата A мають
скiнченнi областi визначення.
Табличний спосiб. Функцiї δ i λ можна задати за допомогою двох таблиць,
якi називають вiдповiдно таблицею переходiв i таблицею виходiв автомата A.
Загальна структура обох таблиць однакова: рядки таблиць позначають вхiдними си-
гналами x
1
, x
2
, ..., x
m
, а стовпчики — станами a
1
, a
2
, ..., a
s
. На перетинi i-го рядка та
j-го стовпчика в таблицi переходiв записують стан δ(a
j
, x
i
), а в таблицi виходiв —
вихiдний сигнал λ(a
j
, x
i
). Iнодi для задання автомата використовують одну сумiще-
ну таблицю (переходiв/виходiв), в якiй на перетинi i-го рядка та j-го стовпчика
записують вiдповiдну пару a
ij
/y
ij
, де a
ij
= λ(a
j
, x
i
) i y
ij
= λ(a
j
, x
i
).
Графiчний спосiб. Це спосiб задання автомата за допомогою орiєнтованого
мультиграфа, який називають графом, або дiаграмою автомата (автоматним
графом або автоматною дiаграмою). Вершини графа позначають символами ста-
нiв автомата A. Якщо δ(a
i
, x
k
) = a
j
i λ(a
i
, x
k
) = y
l
, то у графi автомата проводять
орiєнтовану дугу (або стрiлку) з вершини a
i
у вершину a
j
i позначають цю дугу
символами x
k
/y
l
.
Матричний спосiб. Функцiю переходiв автомата A можна задати за допомо-
гою системи m s × s-матриць переходiв M(x
1
), M(x
2
), ..., M(x
m
). Якщо позначити
m
ij
(x
k
) елемент i-го рядка та j-го стовпчика матрицi M(x
k
), то
m
ij
(x
k
) =
(
1, якщо a
j
= δ(a
i
, x
k
);
0, якщо a
j
6= δ(a
i
, x
k
).
Аналогiчно означають m s × n-матриць виходiв W (x
1
), W (x
2
), ..., W (x
m
) для
функцiї виходiв λ. Якщо позначити w
ij
(x
k
) елемент i-го рядка та j-го стовпчика
матрицi W (x
k
), то
w
ij
(x
k
) =
(
1, якщо y
j
= λ(a
i
, x
k
);
0, якщо y
j
6= λ(a
i
, x
k
).
Приклад 1.1.1. Розглянемо автомат D, який регулює дорожнiй рух на перехре-
стi вулиць В та П.
В автомат дорожнього руху D з перiодом, шо дорiвнює однiй хвилинi, надходить
тактовий сигнал генератора синхроiмпульсiв Г, що послiдовно перемикає сигнали
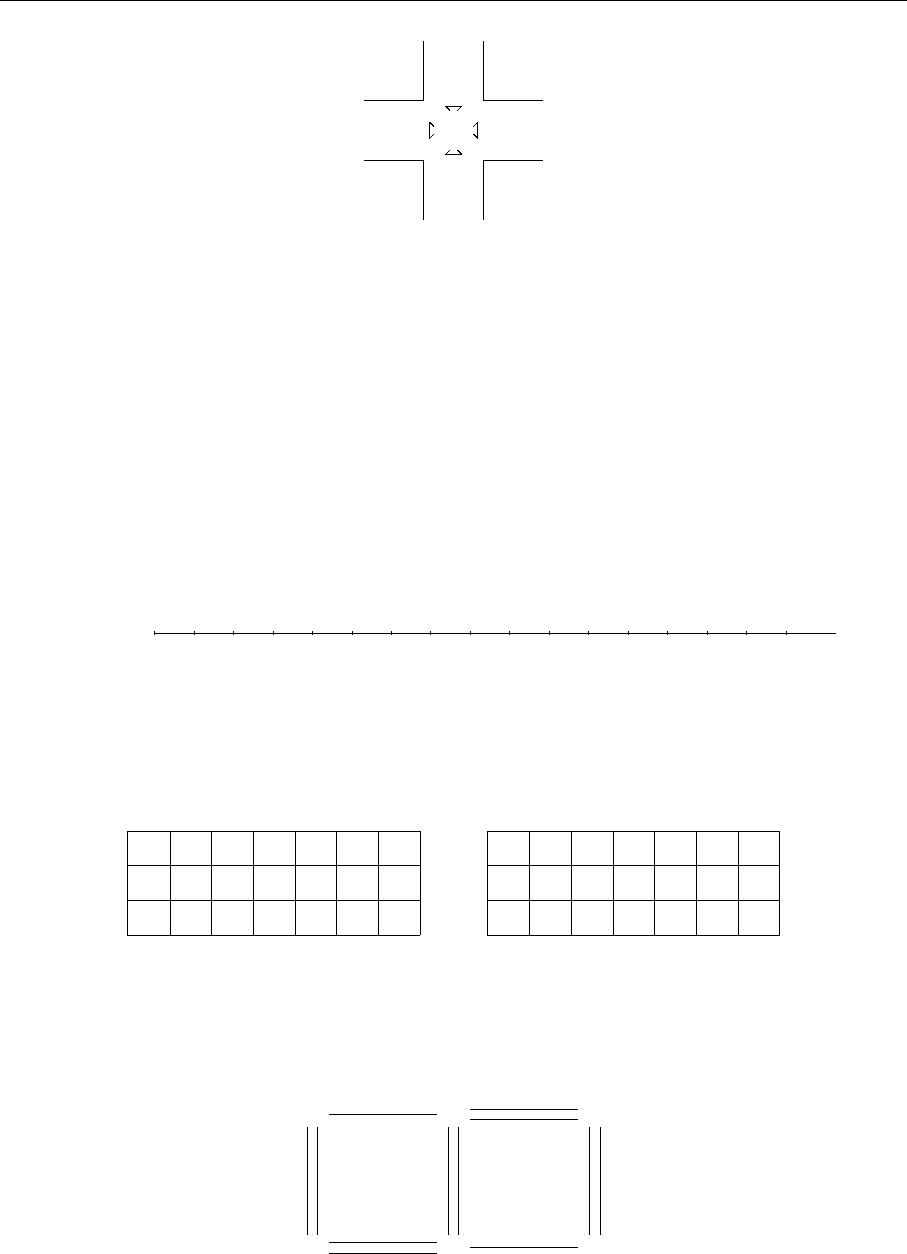
свiтлофора С, дозволяючи транспорту рух вулицями вiдповiдно В i П (рис. 1.1).
Крiм свiтлофора є кнопка виклику К, за допомогою якої пiшохiд може надiслати
автомату запит З на призупинення руху на перехрестi. При надходженнi запиту З
3
Роздiл 1. Теорiя автоматiв
К К
К К
П
В
С
µ´
¶³
d
d
d
d
q
q
q
q
Рис. 1.1. Схематичне зображення регулювання дорожнього руху на
перехрестi
i пiсля завершення поточного iнтервалу часу, що дорiвнює однiй хвилинi, автомат
перериває генерування послiдовностi сигналiв В та П на двi хвилини, сигналом Д
вмикає транспарант, що дозволяє перехiд пiшоходам, а пiсля двох хвилин формує
сигнал скидання СС, повертаючи автомат до вiдновлення формування послiдовностi
сигналiв В та П. Таким чином, автомат D виробляє вихiднi сигнали В, П, Д i СС
дозволу руху транспорту вулицями В i П, дозвiл переходу пiшоходам та скидання
кнопки виклику вiдповiдно. Роботу автомата D iлюструє часова дiаграма на рис. 1.2.
Вхiд Г Г Г Г Г ЗГ Г Г Г Г ЗГ Г Г Г Г Г Г
Час 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
-
Стан a
1
a
2
a
1
a
2
a
1
a
3
a
4
a
2
a
1
a
2
a
5
a
6
a
1
a
2
a
1
a
2
a
1
t
Вихiд В П В П В Д СС П В П Д СС В П В П В
Рис. 1.2. Часова дiаграма роботи автомата дорожнього руху
Таблицi переходiв i виходiв автомата дорожнього руху такi:
δ a
1
a
2
a
3
a
4
a
5
a
6
λ a
1
a
2
a
3
a
4
a
5
a
6
x
1
a
2
a
1
a
4
a
2
a
6
a
1
x
1
y
2
y
1
y
4
y
2
y
4
y
1
x
2
a
3
a
5
a
4
a
2
a
6
a
1
x
2
y
3
y
3
y
4
y
2
y
4
y
1
При цьому використано такi позначення: x
1
= Г, x
2
= З&Г , y
1
= В, y
2
= П ,
y
3
= Д , y
4
= Д &СС .
Задання автомата D за допомогою графа наведено на рис. 1.3.
a
3
x
1
/y
4
²²
x
2
/y
4
²²
a
1
x
2
/y
3
oo
x
1
/y
2
²²
a
6
x
2
/y
1
oo
x
1
/y
1
oo
a
4
x
2
/y
2
//
x
1
/y
2
//
a
2
x
1
/y
1
OO
x
2
/y
3
//
a
5
x
2
/y
4
OO
x
1
/y
4
OO
Рис. 1.3. Граф автомата дорожнього руху
I нарештi, розглянемо метричний спосiб задання функцiй переходiв i виходiв ав-
томата дорожнього руху D. Його матрицi переходiв i матрицi виходiв мають такий
4

1.2. Автоматне вiдображення
вигляд:
M(x
1
) =
0 1 0 0 0 0
1 0 0 0 0 0
0 0 0 1 0 0
0 1 0 0 0 0
0 0 0 0 0 1
1 0 0 0 0 0
, M(x
2
) =
0 0 1 0 0 0
0 0 0 0 1 0
0 0 0 1 0 0
0 1 0 0 0 0
0 0 0 0 0 1
1 0 0 0 0 0
;
W (x
1
) =
0 1 0 0
1 0 0 0
0 0 0 1
0 1 0 0
0 0 0 1
1 0 0 0
, W (x
2
) =
0 0 1 0
0 0 1 0
0 0 0 1
0 1 0 0
0 0 0 1
1 0 0 0
.
Приклад 1.1.2. Побудуємо автомат S, який описує алгоритм функцiонування
послiдовного двiйкового суматора. На вхiд автомата надходять пари розрядiв двiй-
кових чисел, що додаються, починаючи з молодших розрядiв. На виходi автомата
повинен з’являтися розряд результату додавання. Необхiдно також фiксувати i вра-
ховувати ситуацiю наявностi або вiдсутностi перенесення в наступний розряд. Цi двi
ситуацiї вiдображатимуть два стани автомата S: початковому становi a
1
вiдповiдає
ситуацiя «немає перенесення», а стану a
2
— ситуацiя «є перенесення». Вхiднi сигнали
x
0
= (0, 0), x
1
= (0, 1), x
2
= (1, 0) i x
3
= (1, 1) задають чотири можливi комбiнацiї
розрядiв, що додаються.
Граф автомата S подано на рис. 1.4.
a
1
x
4
/0
//
x
1
/0
§§
x
2
/1
((
x
3
/1
EE
a
2
x
1
/1
oo
x
2
/0
§§
x
3
/0
hh
x
4
/1
EE
Рис. 1.4. Граф автомата двiйкового суматора
1.2. Автоматне вiдображення
Нехай у процесi функцiонування заданого автомата A вхiдний сигнал у момент
автоматного часу t = 1 дорiвнює x
i
1
∈ X, у наступний момент t = 2 — x
i
2
∈ X i так
далi, а в момент t = k на вхiд автомата A подається сигнал x
i
k
∈ X, тобто x(1) = x
i
1
,
x(2) = x
i
2
, ..., x(k) = x
i
k
. При цьому кажуть, що на вхiд автомата A подано вхiдне
слово x
i
1
x
i
2
...x
i
k
∈ X
?
.
Для заданого автомата A його функцiї переходiв δ i виходiв λ можна природним
чином поширити з множини U × X на множину U × X
?
, даючи змогу визначати стан
i вихiдний сигнал в автоматi A пiсля подання на його вхiд довiльного вхiдного слова
5

Роздiл 1. Теорiя автоматiв
p = x
i
1
x
i
2
...x
i
k
∈ X
?
. Вважатимемо, що
δ
?
(a
l
, p) = δ(δ(...(δ(δ(a
l
, x
i
1
), x
i
2
), ...), x
i
k−1
), x
i
k
)
i
λ
?
(a
l
, p) = λ(δ(...(δ(δ(a
l
, x
i
1
), x
i
2
), ...), x
i
k−1
), x
i
k
).
Розширену функцiю переходiв δ можна також означити iндуктивно:
1) δ
?
(a
l
, x) для всiх x ∈ X визначається за таблицею переходiв автомата A;
2) для довiльного слова p ∈ X
?
i довiльного вхiдного сигналу x ∈ X
δ
?
(a
l
, px) = δ
?
¡
δ
?
(a
l
, p), x
¢
.
Спираючись на останнє означення, розширену функцiю виходiв λ можна
означити спiввiдношенням
λ
?
(a
l
, px) = λ
¡
δ
?
(a
l
, p), x
¢
, p ∈ X
?
, x ∈ X. (1.2)
Для порожнього слова e ∈ X
?
вважатимемо, що δ
?
(a
l
, e) = a
l
i λ
?
(a
l
, e) = e.
Нехай A/a
1
— iнiцiальний автомат. Для довiльного вхiдного слова p = x
i
1
x
i
2
...x
i
k
вiдповiдне вихiдне слово q ∈ Y
?
означимо так:
q = λ
?
(a
1
, x
i
1
)λ
?
(a
1
, x
i
1
x
i
2
)...λ
?
(a
1
, x
i
1
x
i
2
...x
i
k
).
Означена в такий спосiб вiдповiднiсть мiж вхiдними словами p i вихiдними
словами q називається автоматним вiдображенням, що iндукується автома-
том A/a
1
, i позначається ϕ
A
. Еквiвалентним означенням автоматного вiдображення
ϕ
A
: X
?
→ Y
?
є такi рекурентнi спiввiдношення:
ϕ
A
(e) = e, ϕ
A
(px) = ϕ
A
(p)λ
?
(a
1
, px), p ∈ X
?
, x ∈ X. (1.3)
Автоматне вiдображення часто називають також поведiнкою, або зовнiшньою
поведiнкою, автомата.
Автоматне вiдображення має такi двi важливi властивостi, що випливають без-
посередньо з його означення:
1) |p| =
¯
¯
ϕ
A
(p)
¯
¯
для будь-якого слова p ∈ X
?
, де | · | — довжина слова;
2) якщо p = p
1
p
2
i ϕ
A
(p) = q
1
q
2
, де |p
1
| = |q
1
|, то q
1
= ϕ
A
(p
1
).
Сформульованi властивостi називають умовами автоматностi вiдображення
ϕ
A
.
Поняття автоматного вiдображення можна узагальнити, означаючи аналогiчно
вiдповiднiсть мiж вхiдними i вихiдними словами, яку iндукує автомат A/a
i
, тобто
автомат A, що починає свою роботу зi стану a
i
. Позначатимемо таке автоматне вiд-
ображення ϕ
i
A
.
Усi наведенi означення можна наочно проiлюструвати за допомогою графа ав-
томата. Якщо зафiксувати деякий стан a
i
∈ U в автоматi A, то будь-яке слово
p = x
i
1
x
i
2
...x
i
k
∈ X
?
однозначно визначає шлях довжини k, який веде з вершини
a
i
i складається з k дуг, позначених послiдовно вхiдними сигналами x
i
1
, x
i
2
, ..., x
i
k
.
Тодi δ
?
(a
i
, p) — це остання вершина цього шляху, λ
?
(a
i
, p) — вихiдний сигнал, яким
позначена остання його дуга, а ϕ
i
A
(p) — слово, що утворюється з послiдовностi k
вихiдних сигналiв, написаних на k дугах цього шляху.
6

1.3. Гомоморфiзм, iзоморфiзм i невiдрiзнюванiсть (еквiвалентнiсть) автоматiв
Приклад 1.2.1. Для автомата дорожнього руху D з попереднього роздiлу i
вхiдних слiв p
1
= x
1
x
1
x
2
i p
2
= x
2
x
2
x
1
x
2
маємо: δ
?
(a
1
, p
1
) = a
3
, δ
?
(a
3
, p
1
) = a
5
,
δ
?
(a
4
, p
2
) = a
1
, λ
?
(a
1
, p
1
) = y
3
, λ
?
(a
4
, p
2
) = y
1
, λ
?
(a
2
, p
2
) = y
3
. Крiм того,
ϕ
D
(p
1
) = y
2
y
1
y
3
, ϕ
D
(p
2
) = y
3
y
4
y
2
y
3
, ϕ
2
D
(p
1
) = y
1
y
2
y
3
, ϕ
4
D
(p
2
) = y
2
y
3
y
4
y
1
.
Вiдповiднiстю мiж X
?
i Y
?
, яка задається автоматом A = (X, Y, U, δ, λ),
називається множина T (A) =
©
(v, w) | v ∈ X
?
∧ w ∈ Y
?
∧ ∃ a
i
∈ U : ϕ
i
A
(v) = w
ª
. Вiдпо-
вiднiсть T мiж множинами X
?
i Y
?
називається автоматною, якщо iснує скiнченний
автомат A, для якого T = T (A).
Стан a
j
називається досяжним зi стану a
i
в автоматi A = (X , Y, U, δ, λ ), якщо
iснує таке вхiдне слово v, що a
j
= δ
?
(a
i
, v). Множину всiх станiв автомата A, дося-
жних зi стану a
i
(або зi станiв множини G, G ⊆ U) позначатимемо як D(a
i
) (або
D(G)), а як D
k
(a
i
) (або D
k
(G) для G ⊆ U) — множину станiв, досяжних з a
i
(вiдпо-
вiдно з G) за допомогою вхiдних слiв довжини, що не перевищує k.
Стан a
j
автомата A називається недосяжним зi стану a
i
, якщо не iснує жодного
вхiдного слова, яке переводить автомат A з a
i
в a
j
(тобто a
j
/∈ D(a
i
)).
1.3. Гомоморфiзм, iзоморфiзм i невiдрiзнюванiсть
(еквiвалентнiсть) автоматiв
Нехай A
1
= (X, Y, U
1
, δ
1
, λ
1
) i A
2
= (X, Y, U
2
, δ
2
, λ
2
) — скiнченнi автомати. Вiдобра-
ження γ : U
1
→ U
2
називається гомоморфiзмом автомата A
1
в автомат A
2
, якщо
для будь-яких x ∈ X i a ∈ U
1
виконуються умови
(
γ
¡
δ
1
(a, x)
¢
= δ
2
¡
γ(a), x
¢
,
λ
1
(a, x) = λ
2
¡
γ(a), x
¢
.
(1.4)
Якщо, крiм того, вiдображення γ сюр’єктивне, то воно задає гомоморфiзм авто-
мата A
1
на автомат A
2
. Автомат A
2
називається гомоморфним образом автомата
A
1
.
Якщо вiдображення γ взаємно однозначне i виконуються умови (1.4), то γ на-
зивається iзоморфiзмом автомата A
1
на автомат A
2
. Автомати, для яких iснує
iзоморфiзм, називаються iзоморфними.
Розглянемо пару автоматiв A = (X, Y, U
1
, δ
1
, λ
1
) i B = (X, Y, U
2
, δ
2
, λ
2
). Стан
a
i
∈ U
1
автомата A i стан b
j
∈ U
2
називаються невiдрiзнюваними, якщо для до-
вiльного слова p ∈ X
?
виконується ϕ
i
A
(p) = ϕ
j
B
(p). Iнакше, стани a
i
i стан b
j
вiдрi-
знюванi.
Наведене означення можна використовувати й тодi, коли A = B. У цьому разi
вводять вiдношення невiдрiзнюваностi для рiзних станiв того самого автомата A:
стани a
i
, a
j
∈ U
1
автомата A називаються невiдрiзнюваними, якщо ϕ
i
A
(p) = ϕ
j
A
(p)
для всiх p ∈ X
?
.
Автомати A i B називаються невiдрiзнюваними, якщо для будь-якого стану a ∈ U
1
автомата A iснує невiдрiзнюваний стан b ∈ U
2
автомата B i, навпаки, для для будь-
якого стану d ∈ U
2
автомата B iснує невiдрiзнюваний стан c ∈ U
1
автомата A. Iнiцi-
альнi автомати називають невiдрiзнюваними, якщо їх початковi стани невiдрiзнюва-
нi.
7

Роздiл 1. Теорiя автоматiв
Невiдрiзнюванiсть автоматiв означає, що будь-яке автоматне вiдображення (по-
ведiнка), яке реалiзує один з автоматiв, може бути реалiзоване iншим автоматом.
Iншими словами, невiдрiзнюванi автомати за своєю зовнiшньою поведiнкою подiбнi.
Неважко переконатися, що вiдношення невiдрiзнюваностi H рефлексивне, симетри-
чне i транзитивне i, отже, є вiдношенням еквiвалентностi (вiдповiдно на множинi
станiв або на множинi автоматiв). У зв’язку з цим у лiтературi з теорiї автоматiв
невiдрiзнюванiсть часто називають еквiвалентнiстю. Таким чином, використовують
поняття «еквiвалентнi стани», «еквiвалентнi автомати».
1.4. Мiнiмальний автомат. Алгоритм мiнiмiзацiї
скiнченного автомата
Для множини (класу) K усiх невiдрiзнюваних скiнченних автоматiв мiнiмаль-
ним, або зведеним, називається автомат, який належить цiй множинi й усi рiзнi
стани якого попарно вiдрiзнюванi.
Називатимемо стани a
i
, a
j
∈ U автомата A k-невiдрiзнюваними, якщо
ϕ
i
A
(p) = ϕ
j
A
(p) для всiх вхiдних слiв p довжини k, тобто для всiх p ∈ X
k
. Вiдно-
шення k-невiдрiзнюваностi позначатимемо H
k
, k = 1, 2, ...
Вiдношення H
k
є еквiвалентнiстю на множинi станiв U автомата A.
Фактор-множину U/H
k
позначимо через Q
k
, а класи еквiвалентностi (класи k-
невiдрiзнюваностi) множини Q
k
— C
(k)
i
. Для iндексу класу вибираємо iндекс будь-
якого стану a
i
∈ U, який мiститься в класi C
(k)
i
. Для однозначностi можна брати
найменший з усiх таких iндексiв.
Алгоритм визначення класiв еквiвалентностi на множинi U
1. Стани a
i
, a
j
∈ U належать одному класу 1-невiдрiзнюваностi C
(1)
i
тодi й тiльки
тодi, коли λ(a
i
, x) = λ(a
j
, x) для будь-якого x ∈ X.
2. Стани a
i
i a
j
з одного класу l-невiдрiзнюваностi C
(l)
i
(l > 1) належать одному
класу (l + 1)-невiдрiзнюваностi C
(l+1)
i
тодi й тiльки тодi, коли для будь-якого x ∈ X
стани a
i
1
= δ(a
i
, x) i a
j
1
= δ(a
j
, x) належать тому самому класу l-невiдрiзнюваностi
C
(l)
i
1
.
В iншому випадку, тобто коли iснує такий сигнал x
0
∈ X, що стани δ(a
i
, x
0
) i
δ(a
j
, x
0
) належать рiзним класам l-невiдрiзнюваностi, стани a
i
i a
j
належать до рi-
зних класiв l + 1 -невiдрiзнюваностi C
(l+1)
i
i C
(l+1)
j
. При цьому класи C
(l+1)
i
i C
(l+1)
j
є
пiдкласами (пiдмножинами) класу C
(l)
i
. Казатимемо, що за допомогою вхiдного си-
гналу x
0
здiйснюється розщеплення класу l-невiдрiзнюваностi C
(l)
i
на класи C
(l+1)
i
i
C
(l+1)
j
.
3. Якщо для деякого k жодний з класiв k-невiдрiзнюваностi не розщеплюється на
пiдкласи, тобто для всiх i C
(k)
i
= C
(k+1)
i
, або Q
k
= Q
k+1
, то алгоритм завершує роботу
i одержане розбиття Q
k
є шуканим розбиттям Q множини U на класи еквiвалентних
(невiдрiзнюваних) станiв.
8
1.4. Мiнiмальний автомат. Алгоритм мiнiмiзацiї скiнченного автомата
В iншому випадку (Q
k
6= Q
k+1
) повторюємо крок 2 для розбиття Q
k+1
. Одержав-
ши множину Q класiв еквiвалентностi станiв автомата A, будуємо функцiю переходiв
δ
0
i функцiю виходiв λ
0
мiнiмального автомата Z = (X, Y, Q, δ
0
, λ
0
) за формулами
(
δ
0
¡
[a]
H
, x
¢
=
£
δ(a, x)
¤
H
,
λ
0
¡
[a]
H
, x
¢
= λ(a, x).
(1.5)
Таким чином, задачу мiнiмiзацiї автомата A розв’язано.
Приклад 1.4.1. Розглянемо процедуру мiнiмiзацiї автомата A, таблицi переходiв
i виходiв якого подано на рис. 1.5.
δ a
1
a
2
a
3
a
4
a
5
a
6
a
7
x
1
a
2
a
3
a
6
a
3
a
3
a
4
a
3
x
2
a
1
a
5
a
3
a
7
a
4
a
6
a
2
x
3
a
7
a
4
a
3
a
2
a
5
a
5
a
4
λ a
1
a
2
a
3
a
4
a
5
a
6
a
7
x
1
y
1
y
1
y
1
y
1
y
1
y
1
y
1
x
2
y
2
y
2
y
2
y
2
y
2
y
2
y
2
x
3
y
2
y
1
y
1
y
1
y
1
y
2
y
1
Рис. 1.5. Таблицi переходiв i виходiв автомата A
За таблицею функцiї виходiв λ одержимо розбиття Q
1
на класи 1-
невiдрiзнюваностi, об’єднуючи в класи еквiвалентностi стани, стовпчики значень
для яких у цiй таблицi збiгаються: Q
1
=
©
C
(1)
1
, C
(1)
2
ª
, де C
(1)
1
= {a
1
, a
6
},
C
(1)
2
= {a
2
, a
3
, a
4
, a
5
, a
7
}. Вiдтак будуємо допомiжну таблицю для розбиття Q
1
, замi-
нюючи в таблицi переходiв автомата A стани на вiдповiднi класи 1-невiдрiзнюваностi
(рис. 1.6).
δ
(1)
C
(1)
1
C
(1)
2
a
1
a
6
a
2
a
3
a
4
a
5
a
7
x
1
C
(1)
2
C
(1)
2
C
(1)
2
C
(1)
1
C
(1)
2
C
(1)
2
C
(1)
2
x
2
C
(1)
1
C
(1)
1
C
(1)
2
C
(1)
2
C
(1)
2
C
(1)
2
C
(1)
2
x
3
C
(1)
2
C
(1)
2
C
(1)
2
C
(1)
2
C
(1)
2
C
(1)
2
C
(1)
2
Рис. 1.6. Таблиця переходiв автомата A пiсля розбиття на класи
1-невiдрiзнюваностi
За допомогою одержаної таблицi знаходимо класи 2-невiдрiзнюваностi множини
U. Сигнал x
1
здiйснює розщеплення класу 1-невiдрiзнюваностi C
(1)
2
на два класи 2-
невiдрiзнюваностi C
(2)
2
= {a
2
, a
4
, a
5
, a
7
} i C
(2)
3
= {a
3
}. Клас C
(2)
1
не розщеплюється,
оскiльки обидва стовпчики для станiв a
1
i a
6
збiгаються, тобто C
(2)
1
= C
(1)
1
. От-
же, Q
2
=
©
C
(2)
1
, C
(2)
2
, C
(2)
3
ª
. У той самий спосiб будуємо таблицю для розбиття Q
2
(рис. 1.7).
9

Роздiл 1. Теорiя автоматiв
δ
(2)
C
(2)
1
C
(2)
2
C
(2)
3
a
1
a
6
a
2
a
4
a
5
a
7
a
3
x
1
C
(2)
2
C
(2)
2
C
(2)
3
C
(2)
3
C
(2)
3
C
(2)
3
C
(2)
1
x
2
C
(2)
1
C
(2)
1
C
(2)
2
C
(2)
2
C
(2)
2
C
(2)
2
C
(2)
3
x
3
C
(2)
2
C
(2)
2
C
(2)
2
C
(2)
2
C
(2)
2
C
(2)
2
C
(2)
3
Рис. 1.7. Таблиця переходiв автомата A пiсля розбиття на класи
2-невiдрiзнюваностi
Нарештi, при побудовi розбиття Q
3
за допомогою таблицi на рис. 1.7 виникає
ситуацiя, коли жодний з класiв 2-невiдрiзнюваностi не розщеплюється на пiдкласи
(для всiх станiв з одного класу C
(2)
j
, j = 1, 2, 3, усi стовпчики в таблицi збiгаються).
Таким чином, Q
3
= Q
2
i, отже, шукане розбиття Q множини станiв U на класи
невiдрiзнюваностi має такий вигляд: Q =
©
{a
1
, a
6
}, {a
2
, a
4
, a
5
, a
7
}, {a
3
}
ª
. Одержанi
класи невiдрiзнюваностi позначимо b
1
= {a
1
, a
6
}, b
2
= {a
2
, a
4
, a
5
, a
7
}, b
3
= {a
3
} i
побудуємо таблицi переходiв δ
0
i функцiї виходiв λ
0
шуканого мiнiмального автомата
Z = (X, Y, Q, δ
0
, λ
0
) за допомогою таблиць автомата A i формул (1.5) (рис. 1.8).
δ
0
b
1
b
2
b
3
λ
0
b
1
b
2
b
3
x
1
b
2
b
3
b
1
x
1
y
1
y
1
y
1
x
2
b
1
b
2
b
3
x
2
y
2
y
2
y
2
x
3
b
2
b
2
b
3
x
3
y
2
y
1
y
1
Рис. 1.8. Таблицi переходiв i виходiв мiнiмального автомата Z
Множину станiв U заданого автомата A можна розбити на класи невiдрiзнювано-
стi також за допомогою спецiальної таблицi. Пропонований метод є iншою формою
запису основного алгоритму. Опишемо цей метод, iлюструючи його застосування для
автомата A з останнього прикладу.
Побудуємо трикутну таблицю, рядки якої вiдповiдають станам a
2
, a
3
, ..., a
s
, а стов-
пчики — станам a
1
, a
2
, ..., a
s−1
. Клiтинкам таблицi вiдповiдають невпорядкованi пари
станiв {a
i
, a
j
}, i > j (рис. 1.9).
Заповнимо цi клiтинки за таким правилом. Якщо для станiв a
i
i a
j
iснує такий
вхiдний сигнал x ∈ X, що λ(a
i
, x) 6= λ(a
j
, x), то вiдповiдну клiтинку перекреслю-
ємо хрестиком. Таким чином, очевидно, вiдзначатимуться пари станiв, якi не є 1-
невiдрiзнюваними i потрапляють у рiзнi класи 1-невiдрiзнюваностi.
Для автомата A необхiдно, наприклад, перекреслити клiтинки {a
2
, a
1
}, {a
3
, a
1
},
{a
4
, a
1
} тощо. Для пар станiв {a
i
, a
j
}, якi не є 1-невiдрiзнюваними, у вiдповiдну клi-
тинку таблицi запишемо всi пари станiв {a
i
1
, a
j
1
}, в якi переходить автомат A зi
станiв a
i
i a
j
пiд дiєю кожного x ∈ X: a
i
1
= δ(a
i
, x) i a
j
1
= δ(a
j
, x) i такi, що i
1
6= j
1
,
{a
i
, a
j
} 6= {a
i
1
, a
j
1
}.
Одержимо таблицю, яка вiдповiдає етапу побудови розбиття Q
1
i частково мiстить
iнформацiю, яку ранiше можна було одержати з таблицi розбиття Q
1
(див. рис. 1.6).
Таким чином, в одержанiй таблицi необхiдно закреслити клiтинки, якi мiстять
пари, що вiдповiдають закресленим ранiше клiтинкам.
10
