Черняк Ж.А. (сост.) Методические указания и контрольные работы по высшей математике
Подождите немного. Документ загружается.


Будем искать частное решение системы в виде
,,
21
t
eyex
t
λ
λ
γγ
==
где
λ
γ
γ
,21
,
- константы. Подставляя это решение в систему (6), получим систему уравне-
ний для определения
1
γ
и
2
γ
:
⎩
⎨
⎧
=−+
=+−
.0)(
,0)(
222121
212111
γλγ
γγλ
aa
aa
Таким образом, задача нахождения чисел
1
γ
и
2
γ
сводится к задаче нахож-
дения координат собственных векторов матрицы A. Пусть
),(
21111
γγ
p и
),(
22122
γγ
p
- собственные векторы матрицы A. Тогда общее решение системы
(4) имеет вид
12
12
111 2 12
121 2 22
,
,
tt
tt
x
Ce C e
yC e C e
λ
λ
λ
λ
γγ
γγ
⎧
=+
⎪
⎨
=+
⎪
⎩
где
21
,
λ
λ
- корни характеристического уравнения.
.00)det(
2221
1211
=
−
−
⇔=−
λ
λ
λ
aa
aa
EA
В матричном виде
tt
eCeCX
2
22
12
2
1
21
11
1
λλ
γ
γ
γ
γ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
= .
5. Приступая к решению задачи с физическим содержанием, нужно опре-
делить, какую переменную удобнее взять в качестве искомой функции. Далее,
используя физические законы, составить для ее нахождения дифференциальное
уравнение и решить его.
Контрольная работа №7
Ряды
Литература: [2, гл.16,17]; [3, гл.14]; [5, ч.3, гл.9-10]; [12, ч.3].
Основные теоретические сведения
1. Числовой ряд
∑
∞
=
=++++
1
21
......
n
nn
aaaa (7)
называется сходящимся, если существует предел его частичных сумм
∑
=
=
n
k
kn
aS
1
.
Число
n
n
SS
∞→
= lim называется суммой ряда. Если же предел частичных сумм не
существует или равен бесконечности, то ряд называется расходящимся.
Необходимый признак сходимости: если ряд (7) сходится, то
0lim
=
∞→
n
a
n
.
Достаточные признаки сходимости рядов с положительными членами
)0( >
n
a содержатся в следующих теоремах.
Признаки сравнения
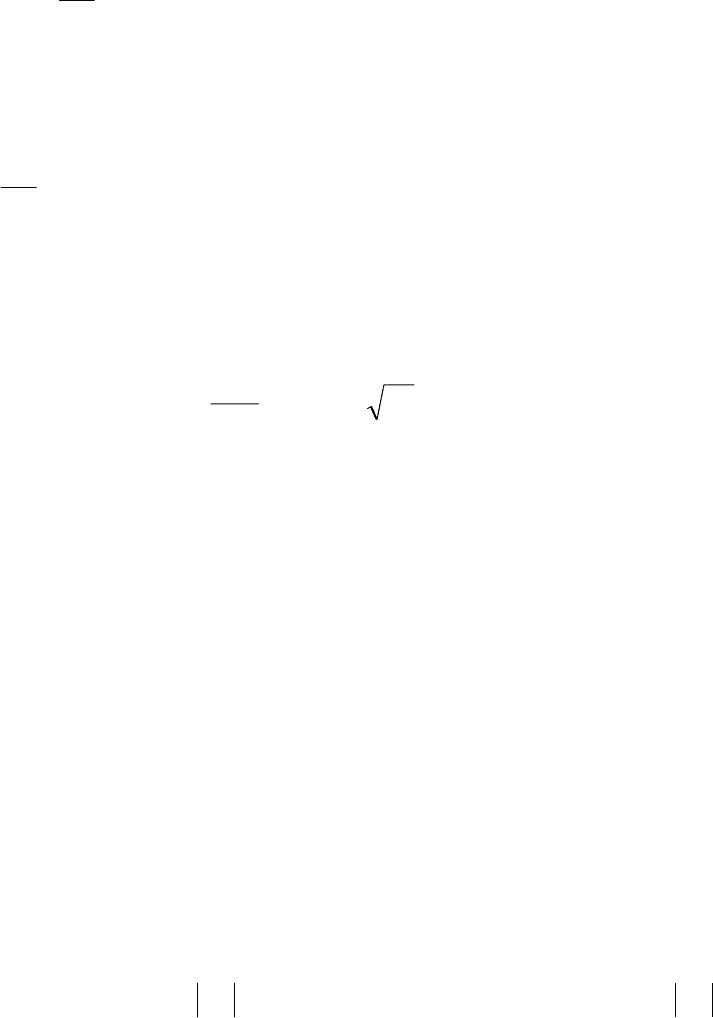
I. Если для любого натурального n выполняются неравенства
n
ba
n
≤
≤
0
,
то из сходимости ряда
n
a
n
∑
∞
=
1
следует сходимость ряда
n
b
n
∑
∞
=
1
, а из расходимо-
сти ряда
n
a
n
∑
∞
=
1
следует расходимость ряда
n
b
n
∑
∞
=
1
.
II. Если
0lim >=
∞→
l
b
a
n
n
n
(здесь 0,0 >>
n
ba
n
), то ряды
n
a
n
∑
∞
=
1
и
n
b
n
∑
∞
=
1
сходятся или расходятся одновременно.
В качестве эталонных рядов для сравнения обычно используют две серии
рядов:
ряды
∑
∞
=
1
1
n
n
α
, сходящиеся при
α
>1 и расходящиеся при 1≤
α
;
ряды
∑
∞
=
−
1
1
n
n
q , сходящиеся при 10
<
≤
q и расходящиеся при .1≥q
Признаки сходимости Даламбера и Коши: если существует предел
)lim(,lim
1
qaq
a
a
n
n
n
n
n
n
==
∞→
+
∞→
,
то ряд
∑
∞
=
1n
n
a сходится при q<1 и расходится при q>1. При q=1 вопрос о сходи-
мости ряда требует дополнительного исследования.
Интегральный признак сходимости: для исследования сходимости ряда
0,
1
>
∑
∞
=
n
n
n
aa рассмотрим интеграл
∫
∞
1
)( dxxf , где )(
x
f
неотрицательна, не-
прерывна и монотонно убывает для ),,1[
+
∞
∈
x
f(n)=a
n
,
N
n ∈ . Тогда ряд
∑
∞
=
1n
n
a и
интеграл
∫
∞
1
)( dxxf одновременно сходятся или расходятся.
Ряд
∑
∞
=
1n
n
a с членами, имеющими разные знаки, называется абсолютно сходя-
щимся, если сходится ряд
∑
∞
=
1n
n
a . Если же ряд
∑
∞
=
1n
n
a сходится, а
∑
∞
=
1n
n
a расхо-
дится, то ряд
∑
∞
=
1n
n
a называется условно сходящимся. Для исследования сходи-
мости знакочередующихся рядов применяется признак Лейбница.
2. Ряд вида

n
n
n
n
n
xxc...)(x-xcxxcc )(...)(
0
0
0010
−=+++−+
∑
∞
=
(8)
называется степенным рядом. Число R называется радиусом сходимости ряда
(2), если при
Rxx <−
0
ряд (8) сходится, а при Rxx >
−
0
расходится. При
Rxx =−
0
ряд (8) может как сходиться, так и расходиться. Радиус сходимости
может быть найден по формулам
1
lim
+
∞→
=
n
n
n
c
c
R или
.
lim
1
n
n
n
c
R
∞→
=
3. Используя известные разложения основных элементарных функций в ряд
Тейлора, можно разложить подынтегральную функцию в ряд и почленно про-
интегрировать (внутри интервала сходимости). Для приближенного вычисления
интеграла с точностью
ε
берется сумма n первых членов про-интегрированного
ряда, где число n определяется исходя из оценки остатка ряда. Если получен-
ный ряд является знакочередующимся, то по теореме Лейбница остаток ряда не
превосходит первого отброшенного члена ряда, взятого по абсолютной величи-
не.
4. Пусть требуется представить в виде ряда решение дифференциального
уравнения
),,( yxy
ϕ
=
′
удовлетворяющее начальному условию y(0)=y
0
. Пред-
положим, что решение y=f(x) уравнения существует и представимо в виде ряда
Тейлора:
...
!2
)0(
!1
)0(
)0()(
2
'''
+++== x
f
x
f
fxfy .
Входящие в этот ряд значения ),...0(),...,0(),0(),0(
)(''' n
ffff можно найти из
исходного уравнения и начального условия. Так, f(0)=y
0
, ).,0()0(
0
'
yf
ϕ
= Далее,
дифференцируя уравнение по x, получаем ),(),(),( xyyxyxy
yx
′
⋅
′
+
′
=
′
′
ϕ
ϕ
откуда
находим ).0()0(
''
fy =
′′
Дифференцируя соотношение для y
′′
еще раз, найдем
)0()0(
'''
fy =
′′′
и т.д.
5. Рядом Фурье периодической функции f(x), lxl
≤
≤
−
называется ряд вида
,sincos
2
)(
1
0
l
nx
b
l
nx
a
a
xf
n
n
n
ππ
++=
∑
∞
=
где
∫
−
=
l
l
n
dx
l
nx
xf
l
a ,cos)(
1
π
n=0,1,2,… ;
∫
−
=
l
l
n
dx
l
nx
xf
l
b ,sin)(
1
π
n=1,2,… .
Для разложения в ряд Фурье четных, нечетных функций, а также непериоди-
ческих функций см. [2, гл.XVII, §3-4].
Контрольная работа №8
Задачи с экономическим содержанием
Литература:[3,гл 3, §3,10; гл.4, §4.4; гл.10, §10.4-10.5; гл.11, §11.3; гл.12, §12.8].
Основные теоретические сведения
1. В математической экономике большую роль играют так называемые про-
дуктивные матрицы. Доказано, что неотрицательная квадратичная матрица яв-
ляется продуктивной тогда и только тогда, когда все её собственные значения
по модулю меньше 1 (первый критерий продуктивности). Неотрицательная
квадратичная матрица А является продуктивной тогда и только тогда, когда для
матрицы Е–А существует
обратная неотрицательная матрица (второй критерий
продуктивности).
2. Чтобы интерпретировать математически закономерности реальных явле-
ний (в том числе и в экономике), формируют соответствующие им математиче-
ские модели. Широкое распространение в экономических исследованиях полу-
чили линейные модели. Они во многих случаях с достаточно высокой точно-
стью соответствуют описываемым явлениям. Почти все линейные модели сво-
дятся к системам алгебраических уравнений
или неравенств. Приведем пример
составления линейной математической модели для конкретной экономической
задачи.
Задача. Три судна доставили в порт 6000 т чугуна, 4000 т железной руды и
3000 т апатитов. Установлены следующие условия разгрузки. Разгрузку можно
осуществлять либо сразу в железнодорожные вагоны (общая вместимость ко-
торых 8000 т), либо в портовые склады. Вагоны должны быть загружены пол-
ностью. Известно также, что поданные в порт вагоны не приспособлены для
перевозки апатитов. Стоимость выгрузки в вагоны 1 т груза каждого вида со-
ставляет соответственно 4,3; 5,25 и 2,2 ден.ед., стоимость отправки 1 т груза на
склад составляет соответственно 7,8; 6,4 и 3,75 ден.ед. Составить математиче-
скую модель условий полной разгрузки судов, при затратах на разгрузки 58850
ден.ед.
Решение. В соответствии с условиями задачи прибывший груз можно либо
отправить в портовые склады, либо загрузить в железнодорожные вагоны.
Обозначим:
x
1
и x
2
(y
1
и y
2
/ z
1
и z
2
) ― количество чугуна (руды / апатитов), разгружаемых
соответственно на склады и в вагоны.
Запишем условия полной разгрузки каждого вида груза:
x
1
+ x
2
= 6000; (9)
y
1
+ y
2
= 4000; (10)
z
1
+ 0 = 3000; (11)

где z
2
= 0, так как по условию задачи апатиты нельзя разгружать в вагоны.
Условие полной загрузки всех поданных вагонов:
x
2
+ y
2
= 8000. (12)
И, наконец, условие, определяющее установленные затраты на разгрузку судов:
4,3x
2
+ 5,25y
2
+ 7,8x
1
+ 6,4y
1
+ 3,25z
1
= 58850. (13)
Итак, условия полной разгрузки судов выражаются системой линейных
уравнений (9-13).
Система (9-13) решается методом Гаусса.
3. Пусть y = f(x) ― дифференцируемая в точке x функция. Эластичностью
функции y = f(x) относительно переменной x называется
)(
/
/
lim
'
0
xf
y
x
xx
yy
x
=
∆
∆
→∆
.
Обозначение эластичности функции y относительно переменной x – E
x
(y).
Величина
E
x
(y) выражает приближенное процентное изменение функции y, со-
ответствующее приращению независимой переменной x на 1%.
Аналогично для функции z = f(x,y), имеющей частные производные
x
z
∂
∂
и
y
z
∂
∂
, вводятся понятия эластичности относительно независимых переменных
x и y. Так, эластичностью E
x
(z) по переменной x называется
E
x
(z) =
x
z
z
x
∂
∂
⋅ ,
а эластичностью E
y
(z) по переменной y
E
у
(z) =
у
z
z
у
∂
∂
⋅ .
4. Издержки производства K однородной продукции есть функция количе-
ства продукции, т. е. K = K(x). Пусть объём продукции меняется от a до b еди-
ниц. Тогда, если функция K(x) непрерывна на [a,b], то среднее значение издер-
жек можно вычислить по теореме о среднем значении интеграла
()
:dxxK
b
a
∫
() ()
dxxK
ab
cK
b
a
∫
−
=
1
.
Решая затем уравнение K(x) = K(c), можно
указать объём продукции x>0, для которого
издержки принимают среднее значение.
Если непрерывная функция f(t) характеризует зависи-
мость производительности труда от времени t, то объём

продукции, произведённой за промежуток времени [t
1
, t
2
],
будет выражаться формулой
∫
=
2
1
)(
t
t
dttfV
.
Условия контрольных работ
Контрольная работа №1
Элементы векторной алгебры, аналитической геометрии
и линейной алгебры
Задачи 1-10. Даны векторы a,b,c,d. Требуется:
– вычислить скалярное произведение векторов из п. 1;
– найти модуль векторного произведения векторов из п. 2;
– проверить коллинеарность и ортогональность векторов из п. 3;
– убедиться, что векторы a,b,c образуют базис;
– найти координаты вектора d в этом базисе.
1. a=i-2j+3k, b=4i+7j+2k, c=6i+4j+2k, d=14i+18j+6k;
1) 3a, 2c; 2) b, -4c; 3) a, c.
2. a=2i-j+11k, b=i+j, c= j+2k, d=2i+5j+3k;
1) 4b, 2c; 2) a, c; 3) b, -c.
3. a=2i+7j+5k, b=i+k, c=i-2j, d=3j+k;
1) 3a, -7b; 2) c, -2a; 3) 3b, c.
4. a=8i+2j+3k, b=4i+6j+10k, c=3i-2j+k, d=7i+4j+11k;
1) 3a, 5c; 2) 2b, 4c; 3) b, -2a.
5. a=3i+j+3k, b=2i+j, c=i+k, d=4i+2j+k;
1) -2b, c; 2) 3a, -5c; 3) b, c.
6. a=10i+3j+k, b=i+4j+2k, c=3i+9j+2k, d=19i+30j+7k;
1) -7a, 4c; 2) 3a, 7b; 3) a, c.
7. a=2i+4j+k, b=i+3j+6k, c=5i+3j+k, d=24i+20j+6k;
1) 3a, -8c; 2) 3b, c; 3) b, c.
8. a=-i+7j-4k, b=-i+2j+k, c=-3j+2k, d=2i+j-k;
1) 5b, 3c; 2) 7a, -4b; 3) c, a.
9. a=3i+j+8k, b=j+3k, c=i+2j-k, d=2i-k;
1) 3a, -2c; 2) 3b, c; 3) a, b.
10. a=4i+7j+8k, b=9i+j+3k, c=2i-4j+k, d=i-13j-13k;
1) -5a, 4b; 2) 8c, -3a; 3) c, b.
Задачи 11-20
. Даны вершины A(x
1
, y
1
), B(x
2
, y
2
), C(x
3
, y
3
) треугольника ABC.
Требуется найти:
1) уравнение стороны AB;

2) уравнение высоты CH и длину этой высоты;
3) уравнение медианы AM;
4) точку N пересечения медианы AM и CH;
5) уравнение прямой, параллельной стороне AB и проходящей через верши-
ну C;
6) внутренний угол при вершине A и внешний угол при вершине C.
11. A(-2,4), B(3,1), C(10,7). 12. A(-3,-2), B(14,4), C(6,8).
13. A(1,7), B(-3,-1), C(11,-3). 14. A(1,0), B(-1,4), C(9,5).
15. A(1,-2), B(7,1), C(3,7). 16. A(-2,-3), B(1,6), C(6,1).
17. A(-4,2), B(-6,6), C(6,2). 18. A(4,-3), B(7,3), C(1,10).
19. A(4,-4), B(8,2), C(3,8). 20. A(-3,-3), B(5,-7), C(7,7).
Задачи 21-30
. Даны четыре точки A
1
(x
1
,y
1
,z
1
), A
2
(x
2
,y
2
,z
2
), A
3
(x
3
,y
3
,z
3
),
A
4
(x
4
,y
4
,z
4
). Требуется найти:
1) уравнение плоскости A
1
A
2
A
3
;
2) уравнение прямой, проходящей через точку A
4
, перпендикулярно плоско-
сти A
1
A
2
A
3
;
3) расстояние от точки A
4
до плоскости A
1
A
2
A
3
;
4) синус угла между прямой A
1
A
4
и плоскостью A
1
A
2
A
3
;
5) косинус угла между координатной плоскостью Oxy и плоскостью A
1
A
2
A
3.
21. A
1
(3,-1,2), A
2
(-1,0,1), A
3
(1,7,3), A
4
(8,5,8).
22. A
1
(3,5,4), A
2
(5,8,3), A
3
(1,2,-2), A
4
(-1,0,2).
23. A
1
(2,4,3), A
2
(1,1,5), A
3
(4,9,3), A
4
(3,6,7).
24. A
1
(0,7,1), A
2
(2,-1,5), A
3
(1,6,3), A
4
(3,-9,8).
25. A
1
(6,1,1), A
2
(4,6,6), A
3
(4,2,0), A
4
(1,2,6).
26. A
1
(7,5,3), A
2
(9,4,4), A
3
(4,5,7), A
4
(7,9,6).
27. A
1
(4,2,5), A
2
(0,7,1), A
3
(0,2,7), A
4
(1,5,0).
28. A
1
(1,-1,3), A
2
(6,5,8), A
3
(3,5,8), A
4
(8,4,1).
29. A
1
(1,-2,7), A
2
(4,2,10), A
3
(2,3,5), A
4
(5,3,7).
30. A
1
(2,3,5), A
2
(5,3,-7), A
3
(1,2,7), A
4
(4,2,0).
Задачи 31-40
. Даны две матрицы A и B. Требуется найти: 1)
T
B
A
+
2
; 2)
A
–1
; 3) EA 32
1
−
−
, где E - единичная матрица третьего порядка.

31.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−−
−−
=
243
678
312
A ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
121
453
212
B .
32.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
100
210
321
A ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−
−
=
354
013
582
B .
33.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
=
101
112
112
A ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−=
321
642
063
B .
34.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−=
121
011
322
A ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
231
720
103
B .
35.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
121
201
213
A ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
173
112
210
B .
36.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−
−
=
111
123
112
A ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
035
213
123
B .
37.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−−
−
=
221
413
432
A ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
291
260
133
B .
38.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
230
494
371
A ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
254
291
256
B .
39.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
110
231
162
A ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
323
504
234
B .
40.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
812
713
301
A ,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−=
465
103
453
B .
Задачи 41-50
. Проверить, совместна ли система уравнений, и в случае со-
вместности решить ее: 1) по формулам Крамера; 2) методом Гаусса; 3) с по-
мощью обратной матрицы (матричным методом).

41.
⎪
⎩
⎪
⎨
⎧
=++
=++
=++
.623
,132
,732
321
321
321
xxx
xxx
xxx
42.
⎪
⎩
⎪
⎨
⎧
−=++
−=++
=
+
−
.344
,42
,322
321
321
321
xxx
xxx
xxx
43.
⎪
⎩
⎪
⎨
⎧
=++
=++
=+−
.325
,642
,123
321
321
321
xxx
xxx
xxx
44.
⎪
⎩
⎪
⎨
⎧
−=+−
=−+
−
=
+
−
.722
,113
,432
321
321
321
xxx
xxx
xxx
45.
⎪
⎩
⎪
⎨
⎧
−=−−
=−+
=+−
.92
,6243
,12423
321
321
321
xxx
xxx
xxx
46.
⎪
⎩
⎪
⎨
⎧
−=−+
=−+
−=
−
+
.534
,2
,4638
321
321
321
xxx
xxx
xxx
47.
⎪
⎩
⎪
⎨
⎧
=−+
−=−+
=−+
.12638
,2
,934
321
321
321
xxx
xxx
xxx
48.
⎪
⎩
⎪
⎨
⎧
−=+
−=+−
=
+
+
.74
,3357
,12432
31
321
321
xx
xxx
xxx
49.
⎪
⎩
⎪
⎨
⎧
−=++
=++
=−−
.35
,1243
,032
321
321
321
xxx
xxx
xxx
50.
⎪
⎩
⎪
⎨
⎧
=++
=++
=
+
+
.123
,032
,432
321
321
321
xxx
xxx
xxx
Задачи 51-60
. Найти собственные значения и собственные векторы мат-
рицы A.
51. .
201
335
212
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−
−
−
=A 52. .
212
044
010
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−=A 53. .
496
375
254
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=A
54. .
776
874
431
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=A 55. .
133
153
131
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−−
−
−
=A 56. .
200
423
334
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−
−
−
=A
57. .
001
010
100
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=A
58. .
520
242
023
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−=A
59. .
284
014
013
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−
−−=A
60. .
250
430
362
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=A
Контрольная работа №2
Введение в математический анализ
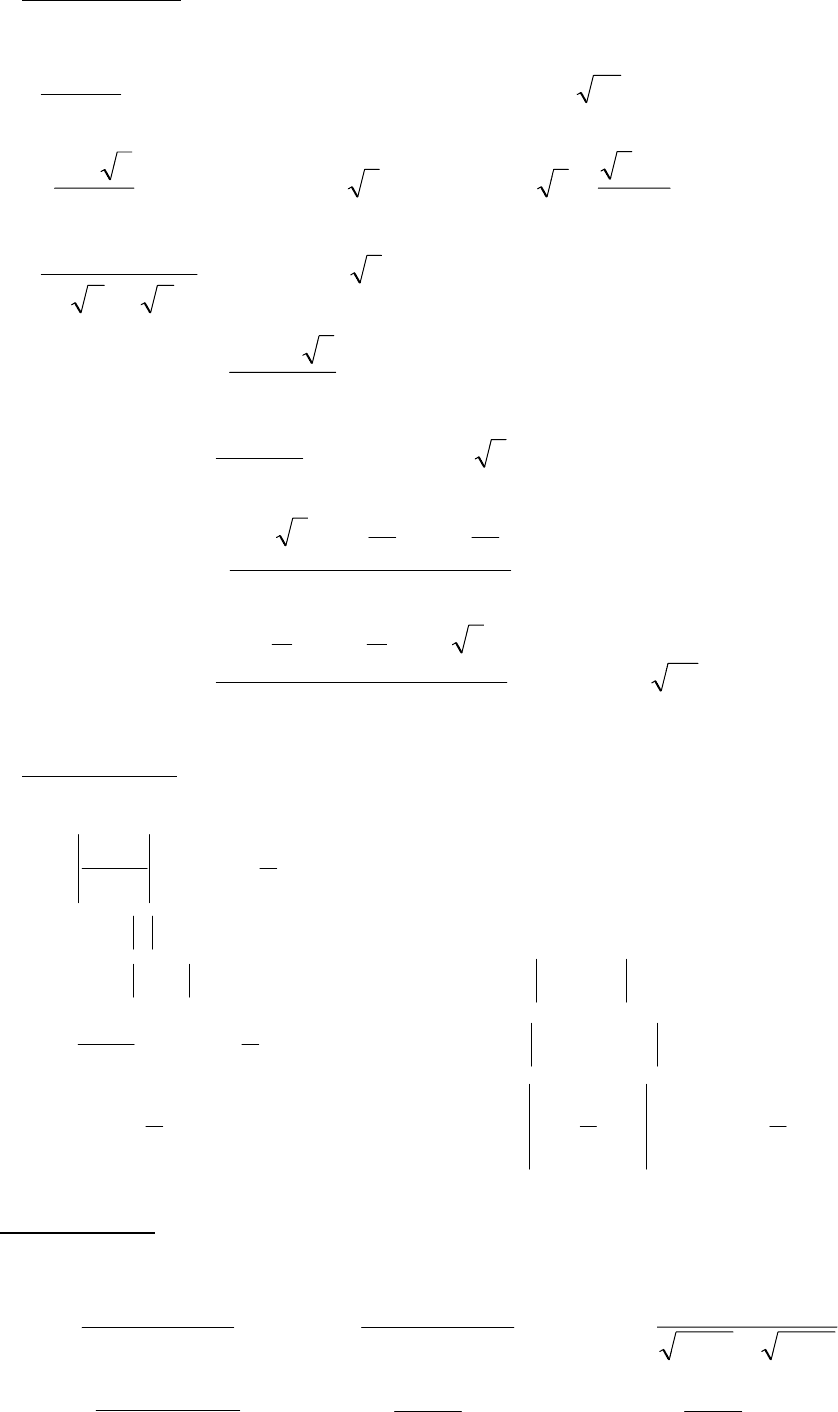
Задачи 61-70. Требуется: 1) выполнить действия над комплексными чис-
лами, записав результат в показательной форме; 2) найти все корни уравнения.
61. 1)
7
9
)1(
)1(
i
i
−
+
; 2) 08
3
=−z . 62. 1)
(
)
5
122 i+ ; 2) 04
4
=
+z .
63. 1)
20
1
31
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
i
i
; 2)
31
5
iz =− . 64. 1)
24
2
3
3
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
i
; 2) 01
6
=
+
z .
65. 1)
(
)
6
7
22
)2(
i
i
+−
; 2) z
4
+8=8 3 i. 66. 1)
(
)
(
)
55
2121 ii −−+ ; 2) z
4
-3z
2
+4=0.
67. 1)
5
58
4
3
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+ ii
; 2) z
4
-30z
2
+289=0.
68. 1)
7
13
)1(
)1(
i
i
−
+
; 2) .031
3
=+− iz
69. 1)
i
ii
−
−−
1
)
12
sin
12
)(cos3(
π
π
; 2) 096
3
=−
−
zz .
70. 1)
(
)
5
7
31
3
sin
3
cos
i
ii +
⎟
⎠
⎞
⎜
⎝
⎛
−
ππ
; 2) .448
3
=+ iz
Задачи 71-80
. Построить график функции y=F(x), используя преобразова-
ния графика известной функции f(x).
71. F(x)=
x
x 12 −
, f(x)=
x
1
.
72. F(x)= )32sin(3
+
x
, f(x)=
x
sin .
73. F(x)= 2
2
−− xx , f(x)=x
2
. 74. F(x)),13cos(2 +
−
=
x
f(x)
x
cos= .
75. F(x) x
−
= 3log
2
, f(x) x
2
log= . 76. F(x)= 65
1
−
−x
, f(x)
x
5= .
77. F(x)=
2
3
−x
x
, f(x)=
x
1
.
78. F(x)= 56
2
−− xx , f(x)=x
2
.
79. F(x)=
⎟
⎠
⎞
⎜
⎝
⎛
−− 1
2
sin
x
, f(x)=
x
sin . 80. F(x)=
1
2
1
1
+
⎟
⎠
⎞
⎜
⎝
⎛
−
x
, f(x)=
x
⎟
⎠
⎞
⎜
⎝
⎛
2
1
.
Задачи 81-90
. Вычислить пределы функций, не пользуясь правилом Лопита-
ля.
81. 1)
1
1052
lim
3
2
1
−
−+
→
x
xx
x
; 2)
3
23
22
375
lim
xx
xx
x
−+
+−
∞→
; 3)
xx
xx
x
−−−
−+
→
42
12
lim
2
3
;
4)
x
xx
x
5
sin3sin
lim
0
−
→
; 5)
13
14
12
lim
−
−∞→
⎟
⎠
⎞
⎜
⎝
⎛
+
−
x
x
x
x
; 6)
24
1
7
lim
−
∞→
⎟
⎠
⎞
⎜
⎝
⎛
+
−
x
x
x
x
.
