Chemin J.-Y., Desjardins B., Gallagher I., Grenier E. Mathematical geophysics
Подождите немного. Документ загружается.

A brief overview of dispersive phenomena 89
Then, functional analysis arguments based upon interpolation results (the
so-called TT
∗
result) imply that
u
L
p
(R;L
q
(R
d
))
≤ C(γ
+
L
1
(R
d
)
+ γ
−
L
1
(R
d
)
) (5.1.9)
for suitable p and q, which is clearly a decay property. Using scaling arguments
and Sobolev embeddings, it can be proved that
∇u
L
2
([0,T ];L
∞
(R
d
))
≤ C
T
γ
+
H
s
(R
d
)
+ γ
−
H
s
(R
d
)
for some s<d/2 depending on the dimension of the space. This kind of
smoothing estimate is used to solve non-linear wave equations locally in time.
The aim of this section is to emphasize basic properties which allow us to
derive dispersion estimates in a much more general framework, as long as waves
propagate in a physical medium. Indeed, the main tool for proving time decay for
solutions of wave equations is multiple integration by parts like in the stationary
phase theorem.
In the next subsection, we shall explain the general way to derive Strichartz
estimates and shall illustrate how this method works on the wave equation in
Subsection 5.1.2.
In Section 5.2, we apply these ideas to the rotating incompressible Navier–
Stokes equations. Dispersion takes place in the direction transverse to the
rotation vector, which influences the time decay of the associated waves in the L
∞
norm. Finally, the application to the non-linear case of the rotating Navier–Stokes
equations is given in Section 5.3.
5.1.1 Strichartz-type estimates
We now intend to describe mathematically dispersion phenomena in terms of
the time decay in the L
∞
norm in the case of frequency localized functions. It
turns out that dispersion is obtained by integration by parts just like in the
proof of the stationary phase theorem. Let d ≥1 and m ≥1 be two integers,
B a bounded open subset of R
d
, and Ω an open subset of R
m
.LetΨ∈D
∞
(B; C)
and a ∈ C
∞
(R
d
×Ω; R). We define K : R ×Ω → C by
K(τ,z)=
R
d
Ψ(ξ) exp(iτ a(ξ, z)) dξ. (5.1.10)
We also introduce the stationary set
X = {(ξ, z) ∈ B × Ω / ∇
ξ
a(ξ,z)=0}.
We assume that the phase a satisfies the bounds
∇a ∈ L
∞
(B ×Ω) and ∇
2
a ∈ L
∞
(B ×Ω). (5.1.11)
We intend to prove the following two theorems.

90 Dispersive cases
Theorem 5.1 Let us consider the non-stationary case X = ∅. Assuming that
inf
B×Ω
|∇
ξ
a|≥β>0, (5.1.12)
then K decays in τ at any order: for any k ∈ N, there exists C
k
> 0 such that
for any τ in R
+
,
K(τ,·)
L
∞
(Ω)
≤ C
k
(1 + τ )
−k
. (5.1.13)
In the stationary case, we shall prove the following result.
Theorem 5.2 Assume that a function ξ
0
exists in C
∞
(Ω; B) such that
X = {(ξ
0
(z),z) ,z∈ Ω} and inf
|x|=1,z∈Ω
|D
2
a(ξ
0
(z),z) · x|≥δ>0. (5.1.14)
Then, there exists C>0 such that for all τ ∈ R
∗
,
K(τ,·)
L
∞
(Ω)
≤ C|τ|
−d/2
. (5.1.15)
Proof of Theorems 5.1 and 5.2 The main idea in proving the above two
theorems is to perform multiple integrations by parts. As a matter of fact, we
introduce the following operator
L =
1 − iα∂
ξ
1+τ|α|
2
,
where α(ξ, z)
def
= ∂
ξ
a(ξ,z). (5.1.16)
It can be easily checked that Lexp(iτa)=exp(iτ a). On the other hand, the
transposed operator
t
L is defined by
R
d
t
Lf · gdx=
R
d
f ·Lgdx for any (f,g) ∈D(R
d
; C)
2
.
Straightforward computations now yield
t
L =
1
1+τα
2
+ i
∂
ξ
α − τα
2
∂
ξ
α
(1 + τα
2
)
2
+
iα
1+τα
2
∂
ξ
. (5.1.17)
It follows from the assumptions of Theorem 5.1 that for all Ψ ∈D(B),
t
LΨ(τ,·)
L
∞
(B×Ω)
≤
C
1+β
2
τ
Ψ
L
∞
(B)
∂
ξ
α
L
∞
(Ω)
+∇Ψ
L
∞
(B)
α
L
∞
(Ω)
.
As a result, it can be deduced by induction that for all k ∈ N
∗
, there exists a
positive C
k
such that for all τ ≥ 0, we have
(
t
L)
k
(τ,·, ·)Ψ
L
∞
(B×Ω)
≤
C
k
(1 + τ )
k
Ψ
W
k,∞
(B)
. (5.1.18)
Writing
K(τ,z)=
R
d
Ψ(ξ) exp(iτ a(ξ, z)) dξ =
R
d
t
L
k
Ψ exp(iτa(ξ, z)) dξ,

A brief overview of dispersive phenomena 91
we deduce from (5.1.18) that
K(τ,·)
L
∞
(Ω)
≤ Vol(B)
C
k
(1 + τ )
k
Ψ
W
k,∞
(Ω)
,
which completes the proof of Theorem 5.1. In order to prove Theorem 5.2, it only
remains to deal with the case when (ξ,z) is localized in a neighborhood B
′
×Ωof
the stationary set X, otherwise Theorem 5.1 would apply and yield the claimed
time decay. For (ξ,z)inB
′
×Ω, we may use the non-degeneracy assumption on
the phase along the stationary set to prove that
|α(ξ,z)|≥|ξ − ξ
0
(z)|
δ
2
·
As a result, we deduce similarly by induction that for k ∈ N and (ξ,z)inB
′
×Ω,
we have
(
t
L)
k
Ψ(τ,ξ,z)
≤
C
k
(1 + τ |ξ − ξ
0
(z)|
2
)
k
ψ
W
k,∞
(B)
. (5.1.19)
For a given integer k greater than d/2, we conclude by making the change of
variables ζ =
|τ|(ξ−ξ
0
(z)) and using the fact that ζ →1/(1+|ζ|
2
)
k
is integrable
over R
d
.
5.1.2 Illustration of the wave equation
Let us consider again the wave equation (5.1.6). Solutions can be expressed in
terms of
u
±
(t, x)=
R
d
γ
±
(ξ) exp(iξ · x ± it|ξ|) dξ. (5.1.20)
The above integral can be rewritten as a function of z = x/t in order to match
the assumptions of Theorem 5.2. It corresponds to the case when
a(ξ,z)=±|ξ| + z · ξ
and to amplitude functions localized in R
d
ξ
\{0}. Observing that
∇
ξ
a(ξ,z)=z ±
ξ
|ξ|
,
we deduce that the phase is likely to be stationary when ξ is directed along z. The
idea is then to write the integration over R
d
as an integration over R ×R
d − 1
for suitable one and d −1 dimensional spaces. Let us assume that the direction
of z is the first vector basis e
1
. Then the phase can be written
a(ξ,z)=ξ
1
z
1
± (|ξ
′
|
2
+ |ξ
1
|
2
)
1/2
with ξ =(ξ
1
,ξ
′
) ∈ R ×R
d−1
and its d − 1 dimensional gradient as
∇
ξ
′
a(z,ξ)=±
ξ
′
|ξ|
,

92 Dispersive cases
so that the stationary set over R
d−1
ξ
′
is given by X = {(ξ
′
=0,z
1
e
1
)}. The second
derivative in ξ
′
of the phase is expressed as
∇
2
ξ
′
a(ξ
1
,ξ
′
,z
1
, 0) =
I
ξ
′
−
ξ
′
|ξ|
⊗
ξ
′
|ξ|
1
|ξ|
,
and hence reduces to I
ξ
′
/|ξ
1
| along the stationary set (we recall that ξ
1
=0is
forbidden since the amplitude function is supported outside {0}). As a result,
Theorem 5.2 applies and yields the claimed time decay (5.1.8) in t
−(d−1)/2
. The
classical estimate (5.1.9) follows from the so–called TT
∗
argument (see [80]).
There are many applications of the above estimates to fluid mechanics prob-
lems such as the low Mach number limit of compressible flows (otherwise known
as the incompressible limit). In the inviscid case, the Euler equations can be
considered in the isentropic case to simplify to
(ALE
comp
)
∂
t
ρ + div (ρu)=0
∂
t
(ρu)+
∇ρ
γ
γε
2
=0,
where γ>1 denotes the exponent of the pressure law and ε the Mach number of
the flow. As the Mach number vanishes, the density tends to a constant, say 1,
and we find div u = 0. Since general initial data do not necessarily have constant
density and incompressible velocity, waves propagate at the very high speed 1/ε.
Introducing the density fluctuation
ψ =
ρ − 1
ε
,
we get the acoustic wave equations
(WE
ε
)
∂
t
u +
∇ψ
ε
=0
∂
t
ψ +
div u
ε
=0
and hence ∂
2
t
ψ − ∆ψ/ε
2
= 0. From the time decay (5.1.8) in L
∞
(R
d
) deduced
from Theorem 5.2, classical duality arguments allow us to derive bounds such
as (5.1.9) for suitable p and q such that q>2. As a result, rescaling the time
according to the speed of sound 1/ε gives convergence to zero at a rate ε. In the
case of the Euler equations for finite time or in the viscous case globally in time,
convergence to the incompressible limit system can be proved for general initial
data, namely the local energy of the potential part of the flow, which is carried
out by the acoustic waves, vanishes as the Mach number tends to zero.
Let us emphasize that a number of physically relevant systems can be studied
similarly, as long as waves propagate in an infinite medium. Indeed, a linear-
ization procedure followed by a travelling wave analysis allows us to derive
dispersion relations expressing the pulsation ω as a function of the wavenumber
ξ. Then, the superposition of such waves can be analyzed like the above simple
example.

The particular case of the Rossby operator in R
3
93
The next section will illustrate once again dispersion effects in a non-linear
system such as the rotating Navier–Stokes equations, which is the main purpose
of this book.
5.2 The particular case of the Rossby operator in R
3
In this section, we give another illustration of the preceding dispersion estimates
on a linearized version of the rotating Navier–Stokes equations. In the sequel,
we shall denote e
3
=(0, 0, 1) the unit vector directed along the x
3
-coordinate,
ε>0 the Rossby number and ν ≥0 the viscosity of the fluid. The inviscid case
ν = 0 can be treated by using Theorem 5.2 and yields a τ
−1/2
time decay in the
L
∞
norm. In the Navier–Stokes-like case ν>0, the viscosity provides additional
regularity which can be used for nonlinear applications, so that the proof is
detailed in the sequel. The model equations read as
(VC
ε
)
∂
t
v − ν∆v +
e
3
∧ v
ε
+ ∇p = f
div v =0
v
|t=0
= v
0
,
which yields in Fourier variables ξ ∈ R
3
(FVC
ε
)
∂
t
v + ν|ξ|
2
v +
ξ
3
ξ ∧ v
ε|ξ|
2
=
f
v
|t=0
= v
0
.
The matrix Mv
def
=
ξ
3
ξ ∧v
|ξ|
2
has three eigenvalues, 0 and ±i
ξ
3
|ξ|
· The associated
eigenvectors are
e
0
(ξ)=
t
(0, 0, 1)
and
e
±
(ξ)=
1
√
2|ξ||ξ
h
|
t
ξ
1
ξ
3
∓ iξ
2
|ξ|,ξ
2
ξ
3
± iξ
1
|ξ|, −|ξ
h
|
2
.
The precise value of these vectors is not needed for our study; all we need to
know is that the last two are divergence-free, in the sense that ξ · e
±
(ξ)=0.
Furthermore they are orthogonal, and we leave the proof of the following easy
property to the reader.
Lemma 5.1 Let v ∈H(R
3
) be given, and define
v
±
def
= F
−1
(v
±
(ξ) · e
±
(ξ))e
±
(ξ)
. (5.2.1)
Then
v
2
L
2
= v
+
2
L
2
+ v
−
2
L
2
.

94 Dispersive cases
We are now led to study
G
ε,±
ν
(τ): g →
R
3
ξ
g(ξ)e
±iτ
ξ
3
|ξ|
−ντε|ξ|
2
+ix·ξ
dξ
=
R
3
ξ
×R
3
y
g(y)e
±iτ
ξ
3
|ξ|
−ντε|ξ|
2
+i(x−y)·ξ
dξdy,
first considering the case when g is supported in C
r,R
for some r<R, defined by
C
r,R
= {ξ ∈ R
3
/ |ξ
3
|≥r and |ξ|≤R}. (5.2.2)
Let us introduce
K
±
(t, τ, z)
def
=
R
3
ξ
ψ(ξ)e
±iτa(ξ,z)+iz·ξ−νt|ξ|
2
dξ, (5.2.3)
where
a(ξ,z)
def
=
ξ
3
|ξ|
,
and ψ is a function of D(R
3
\{0}), such that ψ ≡ 1 in a neighborhood of C
r,R
,
which in addition is radial with respect to the horizontal variable ξ
h
=(ξ
1
,ξ
2
).
As we shall need anisotropic-type estimates in the next section (when we
apply those estimates to the full non-linear rotating fluid equations), it is
convenient to introduce also
I
±
(t, τ, z
h
,ξ
3
)
def
=
R
2
ξ
h
ψ(ξ)e
±iτa(ξ,z
h
)+iz
h
·ξ
h
−νt|ξ|
2
dξ
h
. (5.2.4)
Note that
K
±
(t, τ, z)=
R
e
iz
3
ξ
3
I
±
(t, τ, z
h
,ξ
3
) dξ
3
. (5.2.5)
Lemma 5.2 For any (r, R) such that 0 <r<R, a constant C
r,R
exists such
that ∀z ∈ R
3
, ∀ξ
3
∈ R,
|K
±
(t, τ, z)| + |I
±
(t, τ, z
h
,ξ
3
)|≤C
r,R
min{1,τ
−
1
2
}e
−
ν
2
r
2
t
. (5.2.6)
Proof Due to (5.2.5) and to the fact that ξ
3
is restricted to r ≤|ξ
3
|≤R,itis
enough to prove the result on I
±
and the estimate on K
±
will follow.
The proof of the estimate on I
±
follows the lines of Theorem 5.2 in the
previous section, in a very simple way; the only difference is that we have to take
care of the dependence upon the viscosity. Moreover for the sake of simplicity
we will only consider I
+
, the term I
−
being dealt with exactly in the same way.
First using the rotation invariance in (ξ
1
,ξ
2
), we restrict ourselves to the
case when z
2
= 0. Next, denoting α(ξ)
def
= − ∂
ξ
2
a(ξ)=ξ
2
ξ
3
/|ξ|
3
, we introduce
the following differential operator:
L
def
=
1
1+τα
2
(ξ)
(1 + iα(ξ)∂
ξ
2
) ,
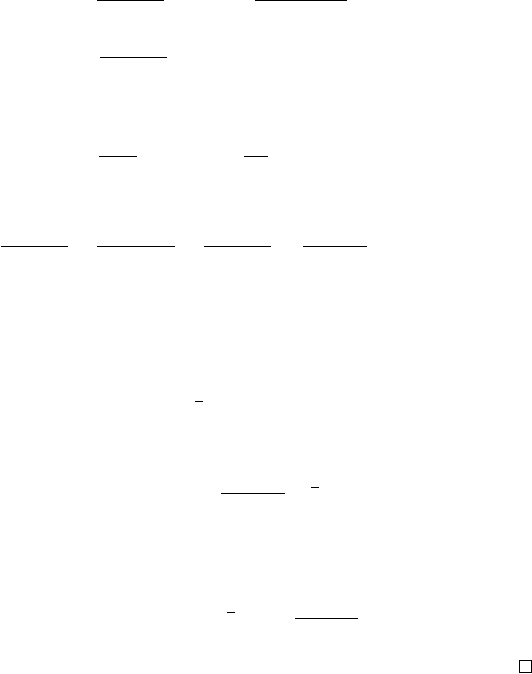
The particular case of the Rossby operator in R
3
95
which acts on the ξ
2
variable, and satisfies L(e
iτa
)=e
iτa
. Integrating by parts,
we obtain
I
+
(t, τ, z
h
,ξ
3
)=
R
2
e
iτa(ξ,z
h
)+iz
1
ξ
1
t
L(ψ(ξ)e
−νt|ξ|
2
)
dξ
h
.
Easy computations yield
t
L
ψ(ξ)e
−νt|ξ|
2
=
1
1+τα
2
− i(∂
ξ
2
α)
1 − τα
2
(1 + τα
2
)
2
ψ(ξ)e
−νt|ξ|
2
−
iα
1+τα
2
∂
ξ
2
e
−νt|ξ|
2
ψ(ξ)
.
As ξ belongs to the set C
r,R
defined by (5.2.2), we have clearly
|ξ
2
|r
R
3
≤|α(ξ)|≤
R
2
r
3
,
hence
1
1+τα
2
+
|1 − τα
2
|
1+τα
2
+
|α|
1+τα
2
≤
C
r,R
1+τξ
2
2
·
An easy computation also shows that |∂
ξ
2
α(ξ)|≤C
r,R
. Finally, since ψ ∈D(R
3
),
we have
∂
ξ
2
e
−νt|ξ|
2
ψ(ξ)
≤|∂
ξ
2
ψ(ξ)|e
−νtr
2
+ νt|ξ
2
||ψ(ξ)|e
−νtr
2
≤ C
r,R
e
−
ν
2
tr
2
.
Putting all those estimates together we infer that
t
L
ψ(ξ)e
−νt|ξ|
2
≤
C
r,R
1+τξ
2
2
e
−
ν
2
tr
2
so since r ≤|ξ
1
|≤R and |e
iτa(ξ,z
h
)+iz
1
ξ
1
| = 1, we obtain, for all z
h
∈ R
2
and
all ξ
3
∈ R,
|I
+
(t, τ, z
h
,ξ
3
)|≤C
r,R
e
−
ν
2
tr
2
R
dξ
2
1+τξ
2
2
,
which proves Lemma 5.2.
Lemma 5.2 yields the following theorem.
Theorem 5.3 For any positive constants r and R such that r<R, let C
r,R
be
the frequency domain defined in (5.2.2). Then a constant C
r,R
exists such that
if v
0
∈ L
2
(R
3
) and f ∈ L
1
(R
+
; L
2
(R
3
)) are two vector fields such that
Supp v
0
∪
t≥0
Supp
f(t, ·) ⊂C
r,R
,
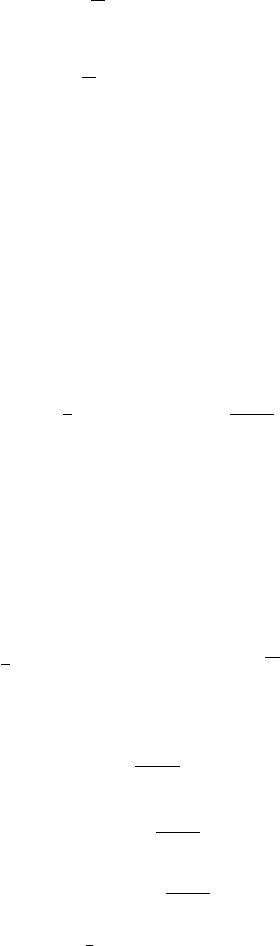
96 Dispersive cases
and if v is the solution of the linear equation (VC
ε
) with forcing term f and
initial data v
0
, then for all p in [1, +∞],
v
L
p
(R
+
;L
∞
(R
3
))
≤ C
r,R
ε
1
4p
v
0
L
2
(R
3
)
+ f
L
1
(R
+
;L
2
(R
3
))
(5.2.7)
and
v
L
p
(R
+
;L
∞,2
x
h
,x
3
)
≤ C
r,R
ε
1
4p
v
0
L
2
(R
3
)
+ f
L
1
(R
+
;L
2
(R
3
))
, (5.2.8)
where we have noted, for (α, β) ∈ [1, +∞]
2
,
f
L
α,β
x
h
,x
3
def
=
f(x
h
, ·)
L
β
(R
x
3
)
L
α
(R
2
x
h
)
.
Proof Let us start by proving estimate (5.2.7). Its anisotropic counterpart
(estimate (5.2.8)) will be obtained in a similar though slightly more complicated
way.
Before proving the result (5.2.7), we note that Duhamel’s formula enables
us to restrict our attention to the case f = 0. Indeed if f is non-zero then we
write v = v
+
+ v
−
with
v
±
(t)
def
= G
ε,±
ν
t
ε
v
±
0
+
t
0
G
ε,±
ν
t − t
′
ε
f
±
(t
′
) dt
′
,
where we have used notation (5.2.1) above. Then by Lemma 5.1 it is enough to
prove the result for v
+
remembering that
v
±
L
2
(R
3
)
≤v
L
2
(R
3
)
and f
±
L
1
(R
+
,L
2
(R
2
))
≤f
L
1
(R
+
,L
2
(R
2
))
.
Note that the eigenvalue 0 does not appear in this formula since the correspond-
ing eigenvector is not divergence-free.
If the result (5.2.7) holds when f
+
= 0, then of course
G
ε,+
ν
t
ε
v
+
0
L
p
(R
+
;L
∞
(R
3
))
≤ C
r,R
ε
1
4p
v
0
L
2
(R
3
)
.
Then we write, if p =1,
G
ε,+
1
(f)
def
=
t
0
G
ε,+
ν
t − t
′
ε
f
+
(t
′
) dt
′
L
1
(R
+
;L
∞
)
≤
t
0
G
ε,+
ν
t − t
′
ε
f
+
(t
′
)
L
∞
dt
′
dt
≤
∞
t
′
G
ε,+
ν
t − t
′
ε
f
+
(t
′
)
L
∞
dtdt
′
≤ C
r,R
ε
1
4
f(t
′
)
L
2
dt
′
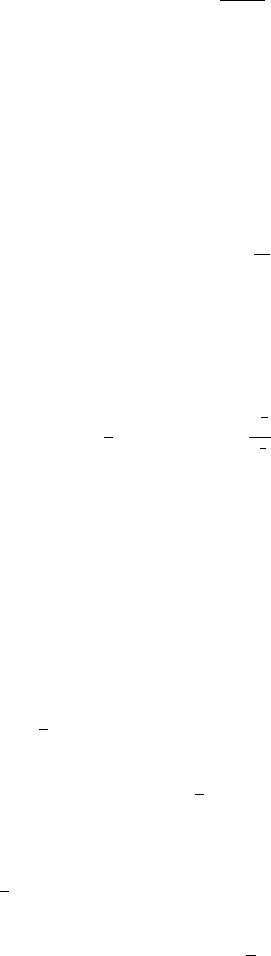
The particular case of the Rossby operator in R
3
97
which yields the result if p = 1. Similarly if p =+∞,
G
ε,+
1
(f) ≤ sup
t≥0
t
0
G
ε,+
ν
t − t
′
ε
f
+
(t
′
)
L
∞
dt
′
≤ C
r,R
sup
t≥0
t
0
f(t
′
)
L
2
dt
′
and estimate (5.2.7), for all p ∈ [1, ∞], follows by interpolation. So from now on
we shall suppose that f =0.
As a consequence of Lemma 5.2, considering g such that g is supported in C
r,R
and ψ ∈D(R
3
\{0}) radial with respect to ξ
h
, such that ψ ≡ 1 in a neighborhood
of C
r,R
, one has
G
ε,+
ν
(τ)g(x)=
R
3
ξ
×R
3
y
ψ(ξ)g(y)e
iτ
ξ
3
|ξ|
−ντε|ξ|
2
+i(x−y)·ξ
dξdy
=
R
3
y
K
+
(ετ,τ,x− y) g(y) dy,
where K
+
is defined by formula (5.2.3). Moreover, the following estimate holds:
G
ε,+
ν
t
ε
g
L
∞
≤ C
r,R
ε
1
2
t
1
2
e
−ct
g
L
1
.
Now we shall use a duality argument, otherwise known as the TT
∗
argument.
Once we have observed that
b
L
1
(R
+
;L
∞
(R
3
))
= sup
ϕ∈B
R
+
×R
3
b(t, x)ϕ(t, x) dxdt,
with
B =
'
ϕ ∈D(R
+
×R
3
), ϕ
L
∞
(R
+
;L
1
(R
3
))
≤ 1
(
,
we can write
G
ε,+
ν
t
ε
g
L
1
(R
+
;L
∞
)
= sup
ϕ∈B
R
+
×R
6
K
+
t,
t
ε
,x− y
g(y)ϕ(t, x) dtdxdy
which can be written
G
ε,+
ν
t
ε
g
L
1
(R
+
;L
∞
)
= sup
ϕ∈B
R
+
×R
3
g(y)
R
3
K
+
t,
t
ε
,x− y
ϕ(t, x)dx
dtdy.

98 Dispersive cases
A Cauchy–Schwarz inequality then yields, denoting
ˇ
b(x)=b(−x),
G
ε,+
ν
t
ε
g
L
1
(R
+
;L
∞
)
≤g
L
2
Φ
with
Φ
def
= sup
ϕ∈B
R
+
ˇ
K
+
t,
t
ε
, ·
∗ ϕ(t, ·) dt
L
2
.
By the Fourier–Plancherel theorem, we have
Φ
2
=
1
(2π)
3
R
+
F
ˇ
K
+
t,
t
ε
, ·
ϕ(t, ·) dt
2
L
2
≤ C
R
+
×R
+
×R
3
K
+
t,
t
ε
, −ξ
ϕ(t, ξ)
K
+
s,
s
ε
, −ξ
ϕ(s, ξ) dξdtds.
By definition (5.2.3) of K,wehave
K
+
(t, τ, −ξ)=ψ(−ξ)e
iτa(−ξ,z)
e
−τt|ξ|
2
.
Thus the following identity holds
K
+
t,
t
ε
, −ξ
K
+
s,
s
ε
, −ξ
=
K
+
t + s,
t − s
ε
, −ξ
ψ(−ξ).
It follows that
Φ
2
≤ C
(R
+
)
2
×R
3
ψ(ξ)F
ˇ
K
+
t + s,
t − s
ε
, ·
∗ ϕ(t, ·)
ϕ(s, ξ) dξdtds.
We now use the Fourier–Plancherel theorem again to get
Φ
2
≤ C
(R
+
)
2
×R
3
ψ(ξ)
ˇ
K
+
t + s,
t − s
ε
, ·
∗ ϕ(t, ·)
(x)ϕ(s, −x) dxdtds,
≤ C
(R
+
)
2
ˇ
K
+
t + s,
t − s
ε
, ·
∗ ϕ(t, ·)
L
∞
ϕ(s, ·)
L
1
dtds,
≤ C
(R
+
)
2
ˇ
K
+
t + s,
t − s
ε
, ·
L
∞
(R
3
)
ϕ(t, ·)
L
1
ϕ(s, ·)
L
1
(R
3
)
dtds.
The dispersion estimate (5.2.6) on K
+
yields
Φ
2
≤ C
r,R
(R
+
)
2
ε
1
2
(t − s)
1
2
e
−νr
2
(t+s)
ϕ(t, ·)
L
1
(R
3
)
ϕ(s, ·)
L
1
(R
3
)
dtds.
Now we conclude simply by writing
Φ
2
≤ C
r,R
ε
1
2
ϕ
2
L
∞
(R
+
;L
1
(R
3
))
(R
+
)
2
1
(t − s)
1
2
dsdt.
