Бухенский К.В. Опорные конспекты по высшей математике. Часть 1

41

Продолжение табл. 3

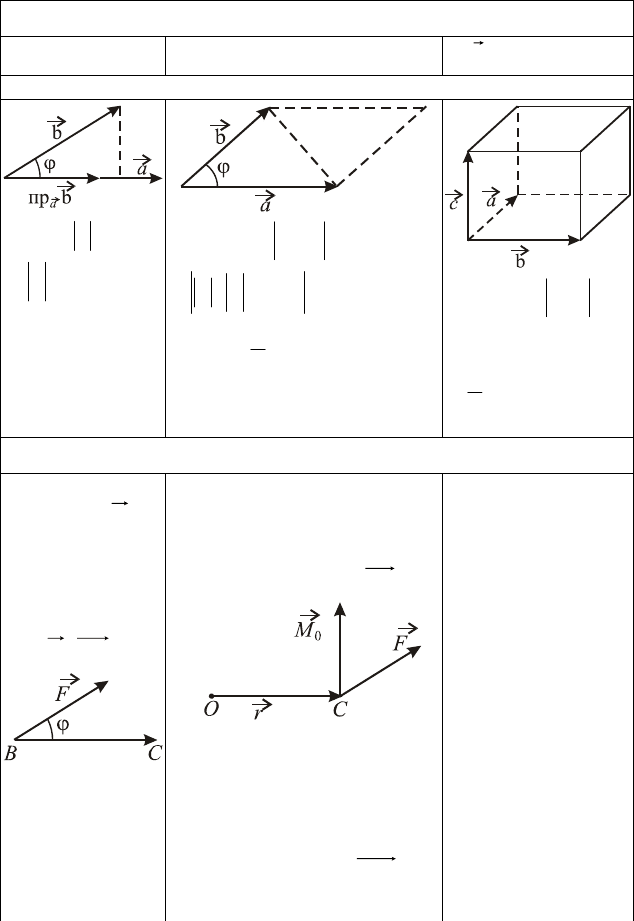
ОБОЗНАЧЕНИЕ

ba

r

⋅

или

(

)

ba

r

,

ba

r

×

или

[

]

ba

r

,

cba

r

или

[

]

cba

r

⋅,

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ

aпрb

bпрaba

b

a

r

=

==⋅

ϕ⋅⋅=

=×=

−

sinba

baS

мапарал

r

мапаралтреуг

SS

−

=

2

1

.

(параллелограмм построен на

векторах

a

r

и

b

r

)

cbaV

дапарал

r

=

−

дапарал

пирамиды

V

−

=

6

1

ФИЗИЧЕСКИЙ СМЫСЛ

Вычисление рабо-

ты

A

силы F

при перемещении

материальной

точки из точки

B

в точку .

C

BCFA ⋅=

1. Вычисление момента

M

v

силы F

v

, приложенной к точке

, относительно точки .

A O

FrM

r

×=

0

, где

OAr =

r

2. Вычисление скорости

v

r

точки

M

твердого тела, вра-

щающегося вокруг неподвиж-

ной оси с угловым уско-

рением

OZ

ω

r

.

rv

r

×

ω

=

, где OMr =

r

,

ω

r

направлен вдоль оси .

OZ

42

Продолжение табл. 3

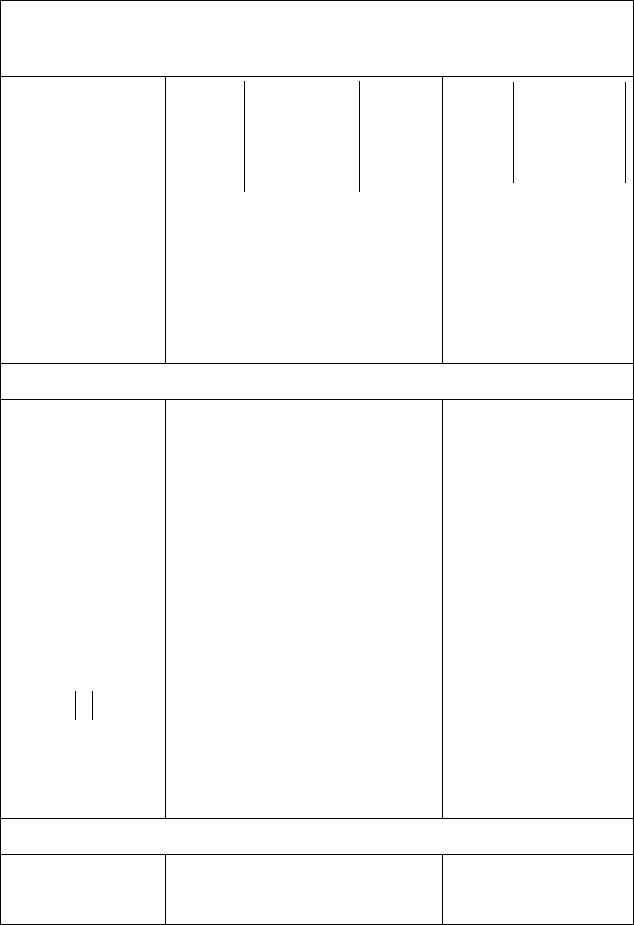
РАСЧЕТ В КООРДИНАТНОЙ ФОРМЕ (ПДСК)

(

)

(

)

(

)

333222111

,,,,,,,, zyxczyxbzyxa ===

r

2121

21

zzyy

xxba

⋅+⋅+

+⋅=⋅

r

()

kyxyx

jzxzx

izyzy

zyx

kji

ba

r

⋅−+

+⋅−−

−⋅−=

==×

1221

222

111

(определитель разложен по

элементам первой строки)

333

222

111

zyx

cba =

r

СВОЙСТВА

1. Переместитель–

ный закон

abba

r

rr

r

⋅=⋅

2. Сочетательный

закон

()

(

)

baba

r

⋅λ=⋅λ

3. Распредели–

тельный закон

(

)

caba

cba

rr

r

⋅+⋅=

=+⋅

4.

2

aa

r

=

(скалярный квад-

р

ат вектора равен

квадрату его дли-

ны)

1. Антипереместительный за-

кон

[

]

[

]

abba

r

,, −=

2. Сочетательны закон й

[

]

[

]

[

]

bababa

r

,,, λ=λ=λ

3. Распределительный закон

[

]

[

]

[

]

cabacba

r

,,, +=+

4.

[

]

0,

r

=aa

1.

[

]

[

]

cbacba

r

,, ⋅=⋅

2. При перестановке

в смешанном произ-

ведении двух векто-

ров его знак меняет-

ся на противополож-

ный:

abcbca

cabcba

r

rr

r

−=−=

=−=

3. Смешанное произ-

ведение не меняется

при круговой пере-

становке векторов:

bacacbcba

r

==

ФАКТЫ, ПОЛЕЗНЫЕ ПРИ РЕШЕНИИ ЗАДАЧ

1. Вычисление

угла между век-

торами:

1. Н. и д. условием коллинеар-

ности ненулевых векторов

a

r

и

1. Н. и д. условием

компланарности трех

ненулевых векторов

43

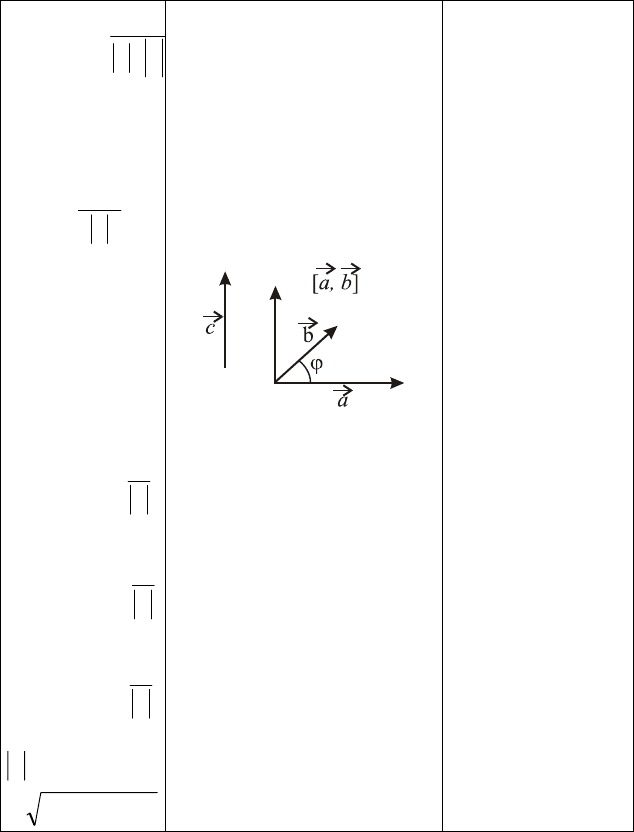
Окончание табл. 3

()

ba

r

⋅

=,cos

2. Вычисление

проекции одного

вектора на дру-

гой:

a

ba

bпр

a

r

⋅

=

3.

⇔⊥ ba

r

0=⋅⇔ ba

r

4. Направляющие

косинусы вектора

(в

ПДСК):

()

zyxa ,,=

r

()

,,cos

cos

a

x

ia

r

==

=α

()

,,cos

cos

a

y

ja

r

==

=β

()

,,cos

cos

a

z

ka

r

==

=

γ

где

222

zyx

a

++=

=

r

b

r

является равенство нулево-

му вектору их в кторного про-

изведения:

е

[

]

0,

r

=ba .

2. Если c

r

ортогонален двум

векторам

a

r

и

b

r

(

)

bcac

r

⊥⊥ ,

, то этот вектор

коллинеарен их векторному

произведению, т.е.

[

]

bac

r

,|| .

cba

r

,, является ра-

венство нулю их

смешанного произ-

ведения:

0=cba

r

.

2. Если

0>cba

r

, то

тройка векторов

cba

r

,, – правая,

если

0<cba

r

, то –

левая



44

ГЛАВА 3. ЛИНЕЙНАЯ АЛГЕБРА

§ 1. Линейное пространство. Преобразование координат

вектора при переходе к новому базису

Опр. 1. Упорядоченная система действительных чисел

n

),...,,(

21 n

α

называется -мерным вектором n a

r

, а числа

n

α

,...,,

21

– его координатами.

Обозначение

),...,,(

21 n

a

α

=

r

.

Опр. 2. Суммой векторов

),...,,(

21 n

a

α

=

r

и

называется вектор

),...,,(

21 n

b

βββ

=

r

),...,,(

2211 nn

ba

βαβαβα

+++=+

r

.

Опр. 3. Произведением вектора

),...,,(

21 n

a

α

=

r

и числа

λ

называется вектор ),...,,(

21 n

a

λα

λ

=

r

.

Следствием суммы векторов и произведением вектора и

числа является разность векторов:

),...,,()1(

2211 nn

baba

βαβαβα

−−−=−+=−

r

.

Линейные операции над -мерными векторами обладают

теми же свойствами, что и линейные операции над векторами на

плоскости и в пространстве.

n

Опр. 4. Множество всех -мерных векторов

n

),...,,(

21 n

a

α

αα=

r

, ni

i

,1, =∈α R , для которых определены

операции сложения и умножения на число, называется арифме-

тическим -мерным векторным пространством

n

R

.

В частности,

2

R

– множество векторов на плоскости,

3

R

–

множество векторов в пространстве. Для пространства

n

R

со-

храняются определения линейной комбинации и линейной зави-

симости векторов

n

aaa

r

,...,

2

,

1

.

Теорема 1. В пространстве

n

R

существует л. нз. век-

торов (это векторы

n

),...,0,...,0,1,0(),0,...,0,1(

21

=

ee

r



).1,...,0,0(=

n

e

r



45

Теорема 2. Любые

1

+

n

векторов в

n

R

л. з.

Из теорем 1, 2 следует, что в

n

R

максимальное число л. нз.

векторов равно

n .

Опр. 5. Базисом в

n

R

называется любая система л. нз.

векторов, число называется размерностью пространства

n

R

.

Как и в случае

2

R

и

3

R

, всякий вектор

n

Ra ∈

r

можно

единственным образом представить как линейную комбинацию

базисных векторов

nnn

eaeaeaeee

r

++=

221121

:,...,,

α

, причем

n

α

,...,,

21

называются координатами вектора a

r

в этом бази-

се.

Пусть – координаты вектора

),...,,(

21 n

xxx

n

Rx ∈

r

в базисе

n

eee

rrr

,...,,

21

, и пусть векторы

n

eee

r

′

,...,,

21

также образуют ба-

зис. Если заданы координаты векторов

n

eee

r

′

,...,,

21

в старом ба-

зисе

n

e

r

ee

rr

,...,,

21

, то есть

⎟

⎠

⎞

⎜

⎝

⎛

=

′

⎟

⎠

⎞

⎜

⎝

⎛

=

′

⎟

⎠

⎞

⎜

⎝

⎛

=

′

nn

n

nn

e

...

...,,

...

,

...

2

1

2

22

12

2

1

21

11

1

rrr

,

и если требуется найти координаты вектора

x

r

в этом базисе, то

следует:

1) составить матрицу перехода от первого базиса ко второ-

му

⎟

⎠

⎞

⎜

⎝

⎛

=

nnnn

n

eee

T

...

............

...

21

22221

11211

,

столбцами которой являются координаты векторов нового бази-

са в старом базисе;



46

2) найти координаты

),...,,(

21 n

xxx

′

вектора x

r

в новом ба-

зисе из матричного уравнения

X

T

X

′

⋅

=

, решение которого

при невырожденной матрице

T

)0( ≠E имеет вид:

X

T

X

⋅

=

′

−1

, где

.

...

,

...

2

1

2

1

⎟

⎠

⎞

⎜

⎝

⎛

′

=

′

⎟

⎠

⎞

⎜

⎝

⎛

=

nn

x

X

x

X

Тогда в новом базисе

n

eee

′′′

r

,...,,

21

вектор x

r

будет иметь

координаты

),...,,(

21 n

xxx

′

, и его можно записать в виде матри-

цы-столбца

⎟

⎠

⎞

⎜

⎝

⎛

′

=

n

x

...

2

1

r

.

Пример 1. А. Убедиться в том, что система векторов

образует базис в

⎟

⎠

⎞

⎜

⎝

⎛

−

=

′

⎟

⎠

⎞

⎜

⎝

⎛

−

=

′

⎟

⎠

⎞

⎜

⎝

⎛

−

=

′

,

3

0

2

,

1

2

1

321

eee

rrr

1

3

R

.

Б. В базисе

321

,, eee

r

задан вектор . Найти коор-

динаты этого вектора в базисе

⎟

⎠

⎞

⎜

⎝

⎛

−

=

1

3

2

x

r

321

,, eee

′′′

r

.

◄ А. Убедимся, что система векторов

321

,, eee

′

r

л. нз. Для

этого составим векторное равенство

0...

2211

r

=

′

++

′

+

′

nn

eee

ααα

. (1)

Приравнивая координаты векторов левой и правой частей

равенства (1), получаем однородную СЛАУ:



47

⎪

⎩

⎪

⎨

⎧

=−⋅+⋅+−⋅

=⋅+⋅+⋅

=−⋅+−⋅+⋅

.0)1(3)1(

,0102

,0)1()2(1

321

ααα

(2)

Найдем определитель основной м. системы (2)

A

011

131

102

121

≠−=

−−

=A

, сл–но, однородная СЛАУ (2)

имеет только нулевое решение

0,0,0

321

=

α

=

α

=

α

, и равен-

ство (1) выполняется только, когда все

321

,,

α

одновременно

равны нулю. Сл–но, по определению, система векторов

321

,, eee

′′′

r

– л. нз. и образует базис в

3

R

.

Б. Составим матрицу перехода от базиса

321

,, eee

r

к базису

321

,, eee

′′′

rrr

:

⎟

⎠

⎞

⎜

⎝

⎛

−−

=

131

102

121

T

.

Обратная ей матрица

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−−−

⋅−=

−

416

321

253

11

1

T

.

Тогда вектор

x

r

в базисе

321

,, eee

′′′

r

имеет вид:

.

1

11

1

3

2

416

321

253

11

1

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅−=

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−−−

⋅−==

′

−

XTX

Это значит

1,1,1

321

=

′

=

′

=

′

xxx и

321321

111 eeeeeex

r

′

+

′

=

⋅

+

⋅

+

⋅

=

+

.►



48

Опр. 6. Линейным (векторным) пространством называ-

ется множество

L

X

, состоящее из элементов любой природы, с

введенными на нем операциями сложения и умножения на дей-

ствительное число, для которых выполняются три условия:

1) сумма

Xyx ∈∀ , Xyx

∈

+

)( ;

2) и

Xx ∈∀ R

∈

α

∀

(

α

– вещественное число) произве-

дение ;

Xx ∈⋅α

3) указанные операции сложения и умножения на число

подчинены следующим аксиомам:

а) Xyx ∈∀ ,

x

y

x

+

=

+

;

б)

Xzyx

∈

∀ ,, )()( zyxzyx

+

=

+

;

в)

∃ нулевой элемент X

∈

Θ

такой, что Xx

∈

∀

xx =+

Θ

;

г)

Xx ∈∀

Xx

∈

−

∃

)( (противоположный) такой, что

Θ

=−+ )( xx ;

д)

Xx ∈∀ xx

=

⋅

1 ;

е) и

Xx ∈∀ R

∈

β

α

∀

, выполняется xx )()(

αβ

β

α

=

;

ж) и

Xx ∈∀

R

∈

β

α

∀

,

выполняется

xxx

β

α

β

α

+

=

+

)(

;

з) и

Xyx ∈∀ , R

∈

α

∀

выполняется yxyx

α

+

=

+

)( .

Элементы л. пр. называются векторами.

Частными случаями л. пр. являются множество веществен-

ных чисел

R

; арифметическое векторное пространство

n

R

;

множество многочленов .

n

nnn

n

axaxaxaxP ++++=

−−

...)(

2

1

10

§ 2. Евклидово пространство

Опр. 1. Л. пр. называется евклидовым, если любым двум его

элементам

x

и

y

ставится в соответствие вещественное число,

которое обозначается и называется скалярным произведе-

нием, подчиненное следующим аксиомам:

),( yx

1) ;

),(),( xyyx =

2)

),(),(),( zyzxyzx

+

=

+ , где – элемент л. пр.; z

3)

),,(),( yxyx

λ

=

где R

∈

λ

;



49

4) , при этом

0),( ≥xx 0),(

=

xx , если

x

– нулевой эле-

мент.

Примером ев. пр. является -мерное векторное простран-

ство

n

R

, в котором скалярное произведение двух векторов

),...,,(

21 n

xxxx =

r

и ),...,,(

21 n

yyyy

=

r

определяется соотноше-

нием

∑

=

+++==

n

i

nnii

yxyxyxyxyx

1

2211

...),(

rr

.

Для скалярного произведения элементов

x

и

y

любого

ев. пр. выполняется неравенство

),)(,(),(

2

yyxxyx ≤ ,

которое называется неравенством Коши-Буняковского.

В частности, для ев. пр.

n

R

неравенство Коши-

Буняковского примет вид:

)....()...(

)...(

22

2

1

22

2

1

2

2211

nn

yyyxxx

yxyxyx

+++⋅+++≤

≤+++

Опр. 2. Нормой элемента

x

в л. пр. называется веществен-

ное число

x , которое ставится в соответствие этому элементу

и подчинено следующим аксиомам:

1)

0≥x

,

0=x

, если

x

– нулевой элемент;

2)

xx ⋅=⋅

λλ

, где R

∈

λ

;

3)

yxyx +≤+ (неравенство Минковского), где –

элемент л. пр.

y

Если л.пр. является ев. пр., то

),( xxx = . В

n

R

норма

вектора

),...,,(

21 n

xxxx =

r

определяется соотношением

22

2

1

...),(

n

xxxxxx +++== .

Опр. 3. Два элемента

x

и ев. пр. называются ортого-

нальными, если

y

0),(

=

yx (их скалярное произведение равно

нулю).



50

Например, векторы и ортогональны, так

как

⎟

⎠

⎞

⎜

⎝

⎛

=

0

1

i

r

⎟

⎠

⎞

⎜

⎝

⎛

=

1

0

j

r

01001),( =⋅+⋅=ji

r

.

Опр. 4. Если норма элемента

x

ев. пр. равна единице

(

1=x ), то

x

называется нормированным.

Опр. 5. Базис векторов

n

eee

r

,...,,

21

-мерного векторного

ев. пр.

n

R

называется ортонормированным, если

⎩

⎨

⎧

==

≠

=

,,1,;,1

,0

),(

njiji

ji

ee

ji

rr

то есть векторы

n

eee

r

,...,,

21

попарно ортогональны.

Если в ев. пр. задан базис

n

eee

r

,...,,

21

, который не являет-

ся ортогональным, то можно построить ортогональный базис

n

eee

′′′

rrr

,...,,

21

по следующим формулам (процесс ортогонализа-

ции Шмидта):

;

11

ee

rr

=

′

,

1

∑

−

=

′

−=

′

k

i

iikk

ecee

v

rr

nk ,...,3,2

=

,

),(

ii

ik

i

ee

c

′′

′

=

rr

r

.

Пример будет рассмотрен в конце этой главы.

§ 3. Линейные операторы (преобразования).

Матрица линейного оператора

Пусть

n

R

L = .

Опр. 1. Линейным оператором

A

~

л. пр. называется за-

кон, по которому каждому вектору ставится в соответст-

вие вектор

L

Lx ∈

r

xAxLx

r

~

: =

′

∈

′

, причем Lyx

∈

∀

r

, справедливо:

1)

yAxAyxA

r

~~

)(

~

+=+

;

2)

),(

~

)(

~

xAxA

r

⋅λ=⋅λ

R

∈

λ

;

где и

xA

r

~

yA

r

~

называются образами векторов x

r

и y

r

.

Бухенский К.В. Опорные конспекты по высшей математике. Часть 1

Подождите немного. Документ загружается.