Бухенский К.В., Елкина Н.В., Маслова Н.Н., Ципоркова К.А. Опорные конспекты по высшей математике. Часть 2
Подождите немного. Документ загружается.


41
Теорема 5 (достаточный признак выпуклости, вогнутости).
Если функция
)(xfy
=
имеет на интервале вторую про-
изводную и
),( ba
0)(
<
′
′
xf
(
)
0)( >
′
′
xf во всех точках интервала
, то график функции
f
ыпуклость и вогну-
тость графика
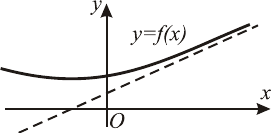
),( ba )(x – выпуклый (вогнутый).
В
функции на-
гляд
но иллюстрируются
удобным для запоминания
“правилом дождя”. Заклю-
чается оно в следующем:
если вторая производная
отрицательна, то говорят,
что “нет дождя” – случай
а) на рисунке, кривая
)(
11
xfy
=
– выпукла ождя» ска-
тываются с выпуклой кровли и под ней сухо.
, «струи д
Если вторая производная положительна, то говорят, что
«есть дождь» – случай б) на рисунке – кривая
)(
22
xfy
=
во-
гнута и «струи дождя» собираются в чаше.
Пример 5. Определить направления выпуклости графика
функции
23
. 43)( −−= xxxf
◄ , ,
43)(
23
−−= xxxf xxxf 63)(
2
−=
′
66)(
−
=
′
′
xxf
.
при , сл-но, здесь график вогнутый.
0)( >
′′
xf 1>x 0)(
<
′
′
xf
при , сл-но, здесь график выпуклый. ►
1<x
Опр. 5. Точка
(
)
(
)
00
, xfxM называется точкой перегиба
графика непрерывной функции
)(xfy
=
, если точка
M
разде-
ляет промежутки, в которых график выпуклый и вогнутый.
42
Теорема 6 (необходимое условие точки перегиба). Пусть
график функции
)(xfy
=
имеет перегиб в точке
(
)
(
)
00
, xfxM
и пусть функция
)(xfy
=
имеет в окрестности точки не-
прерывную вторую производную. Тогда
0
x
(
)
0
0
=
′
′
xf .
Теорема 7 (достаточное условие точки перегиба). Пусть
функция имеет вторую производную в окрестности
точки . Если при переходе через точку
)(xfy =
0
x
0
x )(xf
′
′
меняет свой
знак, то – точка перегиба.
0
x
Пример 6. Найти точки перегиба для функции
43)(
23
−−= xxxf .
◄
,63)('
2
xxxf −= )1(666)(''
−
=
−
=
xxxf , 0)(
=
′
′
xf
при .
1=x 06)0(
<
−
=
′′
f , 06)2( >
=
′
′
f . Следовательно, точка
– точка перегиба графика функции . ►
1=x 43)(
23
−−= xxxf
13.5. Асимптоты графика функции
Опр. 6. Прямая называется асимптотой графика функции
, если расстояние от точки, принадлежащей графику
до этой прямой, стремится к нулю
при неограниченном удалении
точки по графику функции от на-
чала координат.
)(xfy =
Существует два типа асим-
птот: вертикальная и наклонная
(как частный случай наклонной – горизонтальная).
Опр.7. Прямая
a
x
=
называется вертикальной асимпто-
той графика функции
)(xfy
=
, если хотя бы один из односто-
ронних пределов функции или равен
или .
)(lim
0
xf
ax −→
)(lim
0
xf
ax +→
∞+ ∞−
43
Опр. 8. Прямая
bkxy
+
=
называется наклонной асимпто-
той графика функции
)(xfy
=
при
+
∞→
x
(или
−
∞→
x
),
если
0))()((lim
)(
=
+
−
−∞→
+∞→
bkxxf
x
x
.
При наклонная асимптота называется горизонталь-
ной.
0=k
Прямая
bkxy
+
=
является наклонной асимптотой к гра-
фику функции
)(xfy
=
, если существуют пределы
x
xf
k
x
)(
lim
+∞→
= , (19)
[
]
kxxfb
x
−
=
+∞→
)(lim . (20)
В этом случае говорят об асимптоте вправо.
Если хотя бы один из двух пределов (19), (20) не существу-
ет или (
+∞→k
∞
−
), то кривая наклонных асимптот вправо не
имеет.
Аналогичные рассуждения можно провести для
−
∞→
x
(асимптоты влево).
Пример 7. Найти вертикальные асимптоты графика функ-
ции
x
y
1
= .
◄
x
y
1
= , 0
=
x – вертикальная асимптота, так как
+∞=
+→
x
x
1
lim
00
,
−∞=
−→
x
x
1
lim
00
. ►
13.6. Схема исследования функции и построения ее графика
1. Найти область определения функции, ее точки разрыва.
2. Найти точки пересечения с осями.
3. Выяснить является ли функция четной, нечетной или об-
щего вида.
4. Найти асимптоты графика функции.
5. Найти интервалы монотонности и точки экстремума
функции.

44
6. Найти интервалы выпуклости и вогнутости графика
функции и точки перегиба.
7. На основании полученных результатов построить график
функции.
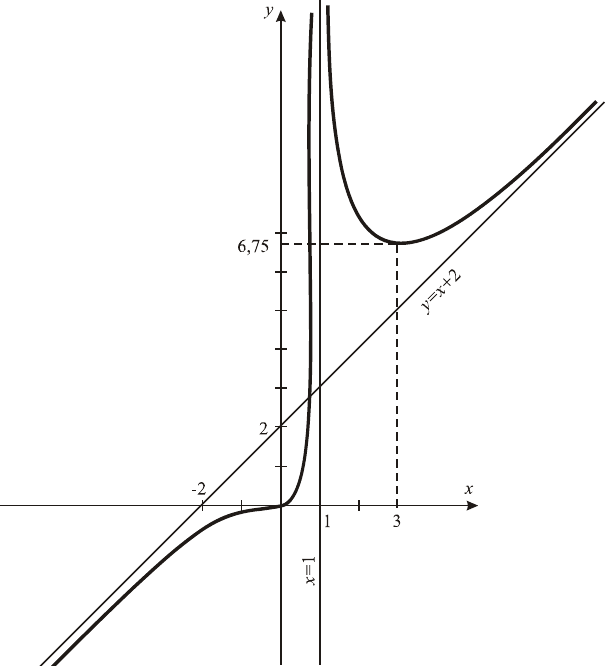
Пример 8. Исследовать функцию
()
2
3
1−
=
x
x
y
и построить
ее график.
◄ Исследование выполним по предложенной схеме.
1. Область определения функции:
),1()1,()(
∞
∪
−
∞=yD
.
2. Найдем точки пересечения графика функции с осями ко-
ординат. Пусть
0
=
õ , тогда 0
=
у . Пусть 0
=
у , тогда
или . Значит, график функции проходит через начало ко-
ординат.
0
3
=х
0=х
3. Проверим, является ли функция четной, нечетной или
общего вида.
()
(
)
()
()
2
3
2
3
11 +
−=
−−
−
=−
х
х
х
х
ху
– функция общего вида.
4. Найдем асимптоты графика функции (вертикальные, на-
клонные, горизонтальные).
Вертикальная асимптота может быть в точке разрыва или на
границе области определения. Здесь вертикальная асимптота
, так как
1=х ∞=
−
−→
2
3
01
)1(
lim
x
x
x
– предел слева в точке 1
=
x ;
()
∞=
−
+→
2
3
01
1
lim
x
x
x
– предел справа.
Наклонные асимптоты вида
bkxy
+
=
найдем, если суще-
ствуют конечные пределы
x
xf
k
x
)(
lim
±∞→
= и
[]
kxxfb
x
−
=
±∞→
)(lim .
В данном случае

45
1
12
1
1
lim
2
lim
)1(
lim
2
23
3
2
3
=
+−
=
+−
=
−
=
±∞→±∞→±∞→
x
x
xxx
x
xx
x
k
xxx
,
2
12
2
lim
)1(
lim
2
2
2
3
=
+−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
±∞→±∞→
xx
xx
x
x
x
b
xx
.
Итак,
2
+
= ху
– уравнение наклонной асимптоты.
5. Найдем промежутки монотонности (возрастания и убы-
вания) функции и точки экстремума.
Находим производную первого порядка.
()
(
)
()
()
()
=
−
−−
=
−
−−−
=
′
3
32
4
3
2
2
1
213
1
1213
х
ххх
х
хххх
у
() ()
(
)
()
3
2
3
23
3
323
1
3
1
3
1
233
−
−
=
−
−
=
−
−−
=
х
хх
х
хх
х
ххх
.
Найдем стационарные и критические точки и выясним зна-
ки на полученных интервалах в окрестности этих точек:
, ,
у
′
0
1
=x 3
2
=x 1
3
=
x – последняя точка не входит в область
определения функции. Используя достаточные признаки экс-
тремума, выясним, как меняет знак при переходе через кри-
тические точки слева направо. Применяем метод интервалов.
ó
′
Так как при переходе через точку 0
=
х производная у
′
знак не меняет (она положительна), то функция монотонно воз-
растает и не является точкой экстремума.
0=х
При переходе через точку
3
=
õ производная у
′
меняет
знак с «–» на «+», значит,
3
=
õ – точка минимума функции и
75,6
4
27
)13(
3
)3(
2
3
min
==
−
== yy .

46
Итак, функция возрастает на промежутках
)1,(
−
∞ и ),3[
∞
,
убывает на промежутке .
]3,1(
6. Найдем промежутки выпуклости и вогнутости графика
функции и точки перегиба.
Для этого вычислим производную второго порядка.
()
(
)
(
)
()
()
=
−
−−−−−
=
′′
6
23
23
2
1
313163
x
xxxxxx
у
()
(
)
(
)
() ()
44
232
1
6
1
33163
−
=
−
−−−−
=
x
x
x
xxxxx
.
Точки, при которых
у
′
′
обращается в нуль или не сущест-
вует, такие:
0
1
=
х
,
1
2
=
х
, но последняя точка не входит в об-
ласть определения функции. Используя достаточные признаки
выпуклости, вогнутости функции, выясним, как меняет знак
у
′
′
при переходе через критические точки слева направо. Применя-
ем метод интервалов.
При переходе через
точку
0=х у
′
′
меняет знак с «–» на «+», значит, 0
=
х – точка
перегиба, - промежуток выпуклости; ,
]0,(−∞ )1;0[ );1(
∞
- про-
межутки вогнутости кривой.
7. Строим график данной функции.
47
Приведем еще примеры эскизов графиков некоторых функ-
ций.

48
49
ГЛАВА 2. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Интегральное исчисление возникло из потребности создать
общий метод нахождения площадей, объемов и центров тяже-
сти. Такой метод применялся еще Архимедом. Систематическое
развитие он получил в 17 веке в работах Б. Кавальери, Э. Тор-
ричелли П. Ферма, Б. Паскаля и других ученых. В 1659 г.
И. Барроу установил
связь между задачей о нахождении площа-
ди и задачей о нахождении касательной. И. Ньютон и
Г. В. Лейбниц в 70-х годах 17 века отвлекли эту связь от упомя-
нутых частных геометрических задач. Тем самым была установ-
лена связь между интегральным и дифференциальным исчисле-
ниями. Эта связь была использована Ньютоном, Лейбницем и
их
учениками для развития техники интегрирования.
Для преодоления трудностей, связанных с интегрировани-
ем, И. Ньютон и Г. В. Лейбниц выражали подынтегральную
функцию в виде многочлена с бесконечным числом членов.
Применяя к таким выражениям обычные правила алгебры, ма-
тематики 18 века сделали множество замечательных открытий.
Однако обнаружилось, что если безоговорочно применять пра-
вила
алгебры к бесконечным суммам, то можно прийти к ошиб-
кам. Стало необходимым точно сформулировать основные по-
нятия и строго доказать свойства бесконечных рядов. Эта задача
была решена математиками 19 века.
Интегральное исчисление позволяет количественно выра-
зить свойства множества объектов в целом или в среднем и
обеспечивает аппарат для сложения большого числа
малых при-
ращений. Своего нынешнего состояния методы интегрирования
в основном достигли в работах Л. Эйлера. Труды М. В. Остро-
градского и П. Л. Чебышева завершили развитие этих методов.

50
§ 1. Элементарные методы интегрирования
Пусть функция
(
)
xf определена на некотором интервале
()
ba, . Тогда функция
(
)
xF называется первообразной для
функции
()
xf на интервале
(
)
ba, , если
(
)
(
)
xfxF
=
′
для всех
()
bax ,∈ .
Теорема. Если функция
(
)
xF является первообразной
функции
()
xf на
(
)
ba, , то множество всех первообразных для
()
xf задается формулой
(
)
СxF
+
, где constC
=
.
Опр. Совокупность всех первообразных для функции
(
)
xf
называется неопределенным интегралом от функции
(
)
xf и
обозначается символом
(
)
∫
dxxf
.
Таким образом, если
(
)
xF – какая-либо первообразная
функции
()
xf , то
(
)
(
)
СxFdxxf
+
∫
=
.
Знак
∫
называется знаком неопределенного интеграла,
()
xf – подынтегральной функцией,
(
)
dxxf – подынтеграль-
ным выражением.
Основные правила интегрирования
Везде далее предполагается, что все рассматриваемые инте-
гралы существуют.
1.
()
(
)
CxFxdF
+
=
∫
.
2.
()
(
)
dxxfdxxfd
=
∫
.
3.
()
(
)
∫
=
∫
dxxfdxxf
α
α
, где const=
α
.
4.
()
(
)
[]
(
)
(
)
∫
+
∫
=
∫
+
dxxgdxxfdxxgxf .
5. Если
(
)
(
)
СxFdxxf
+
∫
=
и 0≠a , то
() ()
∫
++=+ CbaxF
a
dxbaxf
1
.
Последняя формула значительно расширяет таблицу основ-
ных интегралов (см. табл. 2).
