Бухенский К.В., Елкина Н.В., Маслова Н.Н., Ципоркова К.А. Опорные конспекты по высшей математике. Часть 2
Подождите немного. Документ загружается.

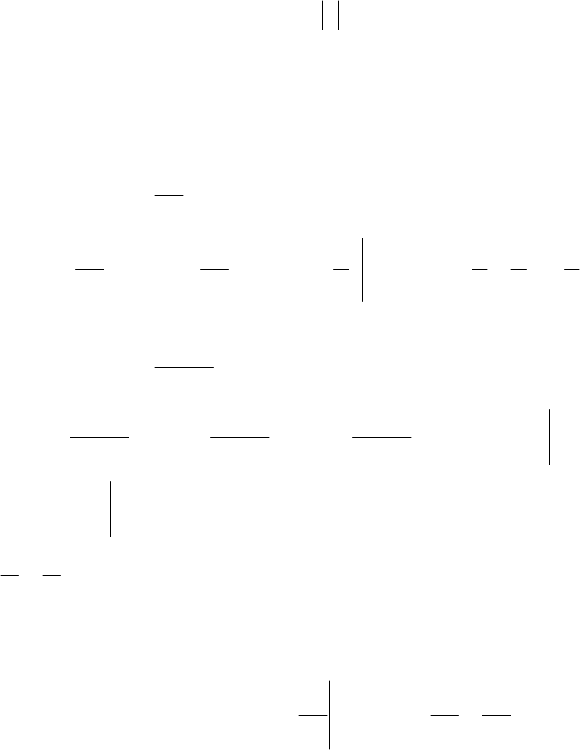
121
()
∫
+∞
∞−
dxxf =
() ()
∫
+
∫
+∞→−∞→
b
c
b
c
a
a
dxxfdxxf
limlim
, ),( bañ
∈
(26)
Иногда будем записывать:
()
∫
+∞
∞−
dxxf =
()
∫
+∞→
−∞→
b
a
b
a
dxxf
lim
.
Замечание 2. В равенстве (26)
+∞→a и
+
∞→b
неоди-
наково (по разным произвольным законам).
Замечание 3. Равенство (26) следует понимать в том смыс-
ле, что если каждый из несобственных интегралов, стоящих в
правой части равенства, сходится, то сходится и интеграл в ле-
вой части.
Пример 3.
∫
−
∞−
2
2
x
dx
.
◄
2
11
2
1
lim
1
limlim
2
2
2
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
+=
⎟
⎠
⎞
⎜
⎝
⎛
−=
∫
=
∫
−∞→
−
−∞→
−
−∞→
−
∞−
ax
x
dx
x
dx
a
a
a
a
a
.
Интеграл сходится. ►
Пример 4.
∫
+
+∞
∞−
2
1 x
dx
.
◄
∫
+
+∞
∞−
2
1 x
dx
= +=
∫
+
+
∫
+
−∞→+∞→−∞→
0
0
2
0
2
lim
1
lim
1
lim
a
a
b
b
a
a
arctgx
x
dx
x
dx
()()
=−+−=+
+∞→−∞→+∞→
0
lim
0
limlim
0
arctgbarctgaarctgx
ba
b
b
π
π
π
=+=
22
.►
Пример 5.
∫
+∞
∞−
xdx .
◄
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−==
∫
=
∫
+∞→
−∞→
+∞→
−∞→
+∞→
−∞→
∞+
∞−
22
lim
2
limlim
222
abx
xdxxdx
b
a
b
a
b
a
b
a
b
a
.
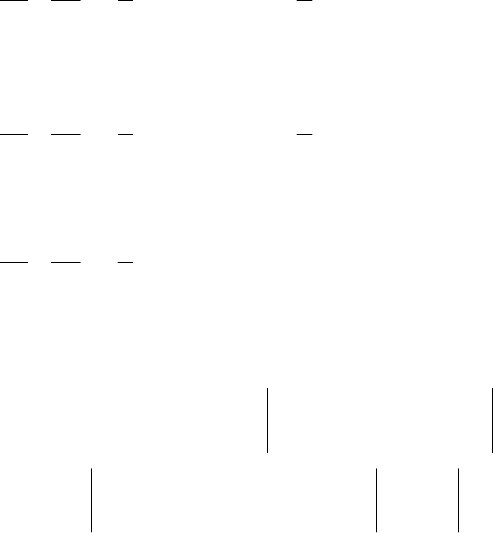
122
Полученный предел не существует (получаем неопределен-
ность
∞−∞ ). Интеграл расходится. ►
Замечание 4 (к примеру 5). Так как
a и b неограниченно
возрастают по абсолютной величине по разным законам, то бу-
дем получать различные значения предела. Например, если
+∞→=−= kkbka ,,
2
, то
() ()
[]
+∞=−=−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+∞→+∞→
+∞→
−∞→
1
lim
2
1
lim
2
1
22
lim
2224
22
kkkk
ab
kk
b
a
.
Если
+∞→=−= kkbka ,,
2
, то
() ()
[]
−∞=−=−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+∞→+∞→
+∞→
−∞→
2242
22
1
lim
2
1
lim
2
1
22
lim
kkkk
ab
kk
b
a
.
Если
+
∞→
=
−
= kkbka ,, , то
()
0
lim
2
1
22
lim
22
22
=−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+∞→
+∞→
−∞→
kk
ab
k
b
a
.
Пример 6.
∫
∞−
0
cos xdxx .
◄
=
==
==
=
∫
=
∫
−∞→
∞−
xvxdxdv
dxduxu
xdxxxdxx
a
a
sincos
cos
lim
cos
00
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∫
−=
−∞→−∞→
00
0
0
cossin
lim
sinsin
lim
aa
a
a
a
a
xxxdxxx
aaa
aa
cos
lim
1sin
lim
0
−∞→−∞→
−
+
−=
.
Интеграл расходится, так как
aa
a
sin
lim
−∞→
и a
a
cos
lim
−∞→
не
существуют. ►

123
Опр. 4. Величина
() () ()
∫
=
⎟
⎠
⎞
⎜
⎝
⎛
∫
+
∫
+∞
∞−−
∞→
dxxfPVdxxfdxxf
a
c
c
a
a
..
lim
, ),( aañ
−
∈
, (27)
(в случае его существования) называется главным значением не-
собственного интеграла
()
∫
+∞
∞−
dxxf . Справа в формуле (27) напи-
сано обозначение главного значения.
К примеру,
0
22
limlim
..
22
0
0
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
∫
+
∫
=
∫
∞→
−
∞→
∞+
∞−
aa
xdxxdxxdxPV
a
a
a
a
.
Замечание 5. Если несобственный интеграл сходится, то
его значение совпадает с его главным значением.
10.2. Признаки сходимости несобственных интегралов
с бесконечными пределами
Теорема 1. Пусть на промежутке
[
)
+
∞,a каждая из функ-
ций
()
xf и
(
)
x
ϕ
удовлетворяет условиям определения 1 и для
всех
()
axx ≥
выполняется неравенство:
(
)()
xxf
ϕ
≤
≤
0 .
Тогда: 1) из сходимости интеграла
()
∫
+∞
a
dxx
ϕ
следует схо-
димость интеграла
()
∫
+∞
a
dxxf
, при этом
() ()
∫
≤
∫
+∞+∞
aa
dxxdxxf
ϕ
;
2) из расходимости интеграла
()
∫
+∞
a
dxxf следует
расходимость интеграла
()
∫
+∞
a
dxx
ϕ
.
Пример 7. Исследовать на сходимость
()
∫
+
+∞
1
2
3
x
ex
dx
.
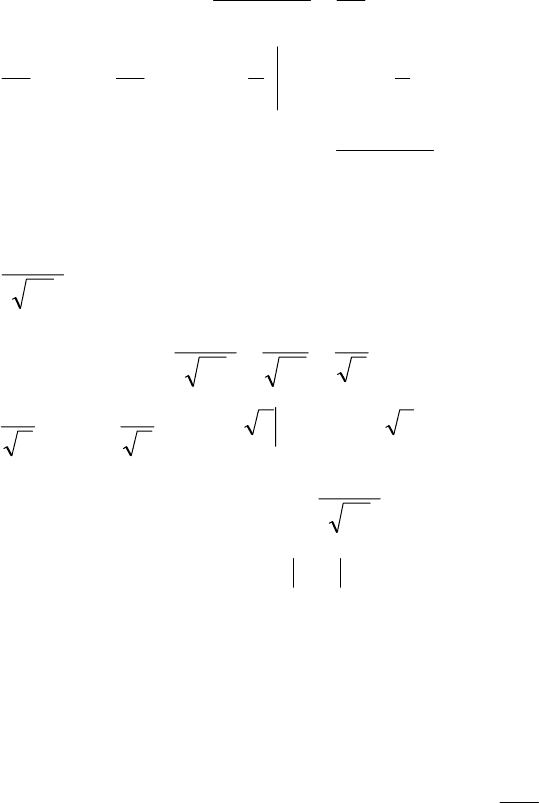
124
◄ При 1≥x имеем
()
22
1
3
1
xex
x
≤
+
.
11
1
lim
1
limlim
1
1
2
1
2
=
⎟
⎠
⎞
⎜
⎝
⎛
+−=
⎟
⎠
⎞
⎜
⎝
⎛
−=
∫
=
∫
+∞→+∞→+∞→
∞+
bx
x
dx
x
dx
b
b
b
b
b
.
Сл–но, по теореме 1 интеграл
()
∫
+
+∞
1
2
3
x
ex
dx
сходится и его
значение меньше 1. ►
Пример 8. Исследовать на сходимость интеграл
∫
+
∞+
9
5
2
3
dx
x
x
.
◄ При
9≥x
x
x
x
x
x 13
5
2
5
2
=≥
+
.
(
)
+∞=−==
∫
=
∫
+∞→+∞→+∞→
+∞
3
lim
2
lim
2
lim
9
99
bx
x
dx
x
dx
b
b
b
b
b
.
Тогда по теореме 1 интеграл
∫
+
∞+
9
5
2
3
dx
x
x
расходится. ►
Теорема 2. Если интеграл
()
∫
+∞
a
dxxf сходится, то сходит-
ся и интеграл
()
∫
+∞
a
dxxf .
В этом случае интеграл
()
∫
+∞
a
dxxf
называется абсолютно
сходящимся.
Пример 9. Исследовать на сходимость интеграл
∫
+∞
1
3
sin
dx
x
x
.

125
◄ Подынтегральная функция – знакопеременная. Кроме
того:
33
1sin
xx
x
≤
для всех
[
)
+
∞
∈
,1x
. Но интеграл
∫
+∞
1
3
x
dx
схо-
дится (см. пример 1). Тогда по теореме 1 сходится интеграл
∫
+∞
1
3
sin
dx
x
x
, сл–но, сходится и интеграл
∫
+∞
1
3
sin
dx
x
x
.►
10.3. Интегралы от неограниченных функций
(несобственные интегралы II рода)
Опр. 5. Пусть функция
(
)
xf определена на промежутке
[
)
ba,
, интегрируема на любом промежутке
[
]
ε
−
ba,
, принад-
лежащем промежутку
[
)
ba,
(
)
0>
ε
, и неограничена в окрест-
ности точки
b . Если существует конечный предел
()
∫
−
+→
ε
ε
b
a
dxxf
lim
0
, то этот предел называется несобственным инте-
гралом от функции
(
)
xf на промежутке
[
)
ba, и обозначается
()
∫
b
a
dxxf .
Т.о. имеем:
()
∫
b
a
dxxf =
()
∫
−
+→
ε
ε
b
a
dxxf
lim
0
. (28)
Если существует конечный предел
()
∫
−
+→
ε
ε
b
a
dxxf
lim
0
, то гово-
рят, что интеграл
()
∫
b
a
dxxf сходится, в противном случае – рас-
ходится.
Опр. 6. Если функция
(
)
xf определена на промежутке
(
]
ba, , интегрируема на любом промежутке
[
]
ba ,
ε
−
, принад-
лежащем промежутку
(
]
ba,
(
)
0>
ε
, и неограничена в окрест-
ности точки
a , то полагаем
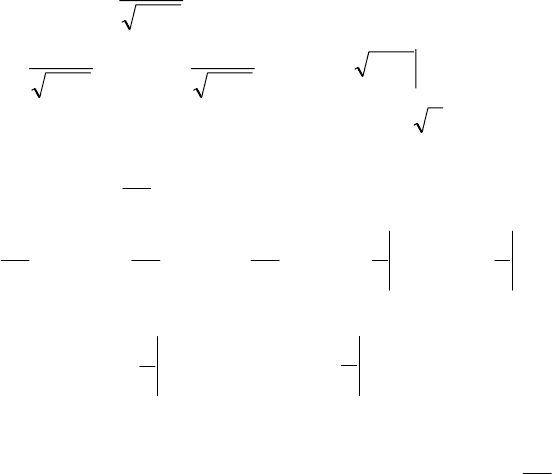
126
()
∫
b
a
dxxf =
()
∫
+
+→
b
a
dxxf
ε
ε
lim
0
. (29)
Опр. 7. Если функция
(
)
xf определена на промежутках
[
)
ca,
и
(
]
bc,
, интегрируема на отрезках
[
]
1
,
ε
−
ca
и
[
]
bc ,
2
ε
−
,
принадлежащих промежуткам
[
)
ca, и
(
]
bc, соответствен-
но
()
0,0
21
>>
ε
ε
, и неограничена в окрестности точки c , то
полагаем
()
∫
b
a
dxxf =
() ()
∫
+
∫
+
+→
−
+→
b
с
с
a
dxxfdxxf
2
2
1
1
limlim
00
ε
ε
ε
ε
.
Пример 10.
∫
−
1
0
1 x
dx
.
◄
=−−=
∫
−
=
∫
−
−
+→
−
+→
ε
ε
ε
ε
1
0
0
1
0
0
1
0
1
lim
2
1
lim
1
x
x
dx
x
dx
(
)
21
lim
2
0
=−−=
+→
ε
ε
.►
Пример 11.
∫
−
1
1
2
x
dx
.
◄
1
0
1
0
1
2
0
1
2
0
1
1
2
2
2
1
1
2
2
1
1
1
lim
1
limlimlim
ε
ε
ε
ε
ε
ε
ε
ε
xx
x
dx
x
dx
x
dx
+→
−
−
+→+→
−
−
+→
−
−−=
∫
+
∫
=
∫
.
Каждый из двух полученных пределов равен
∞
:
∞=−
−
−
+→
1
1
1
0
1
lim
ε
ε
x
и
∞=−
+→
1
0
2
2
1
lim
ε
ε
x
.
Сл–но, первый интеграл расходится на промежутке
[
]
0,1
−
,
а второй – на отрезке
[
]
1,0 . Окончательно имеем: интеграл
∫
−
1
1
2
x
dx
расходится на всем отрезке
[
]
1,1
−
.►
Замечание 6. Если функция
(
)
xf , определенная на отрезке
[]
ba,
, имеет внутри этого отрезка конечное число точек разрыва

127
n
aaa ,,,
21
K , то интеграл от функции
(
)
xf
на отрезке
[
]
ba,
определяется следующим образом:
() () () ()
∫
++
∫
+
∫
=
∫
b
a
a
a
a
a
b
a
n
dxxfdxxfdxxfdxxf K
2
1
1
,
если каждый из несобственных интегралов в правой части ра-
венства сходится. Если хотя бы один из этих интегралов расхо-
дится, то и
()
∫
b
a
dxxf называется расходящимся.
Опр. 8. Если функция
(
)
xf удовлетворяет условиям опре-
деления 7, то величина
() () ()
∫
=
⎟
⎠
⎞
⎜
⎝
⎛
∫
+
∫
+
−
+→
b
a
b
c
c
a
dxxfPVdxxfdxxf ..
lim
0
ε
ε
ε
(если предел существует) называется главным значением несоб-
ственного интеграла
()
∫
b
a
dxxf (см. определение 7;
ε
ε
ε
=
=
21
).
Пример 12. Найти главное значение интеграла
∫
−
3
1
2x
dx
.
◄
+−=
∫
−
+
∫
−
=
∫
−
−
+→
+
+→
−
+→
1
1
2
1
1
1
2
1
0
3
2
0
2
1
0
3
1
2ln
lim
2
lim
2
lim
2
ε
ε
ε
ε
ε
ε
x
x
dx
x
dx
x
dx
()
2
1
0
0
21
0
0
3
2
0
ln
lim
ln1ln1lnln
lim
2ln
lim
2
1
2
1
2
2
ε
ε
εε
ε
ε
ε
ε
ε
ε
+→
+→
+→
+→
−
+→
=−+−=−+ x
.
Величина предела зависит от того, по какому закону стре-
мятся к нулю
1
ε
и
2
ε
, следовательно, интеграл расходится. Ес-
ли же взять
ε
ε
ε
=
=
21
, то 01ln
2
..
3
1
==
∫
−x
dx
PV
.►

128
10.4. Признаки сходимости
несобственных интегралов II рода
Теорема 3. Пусть на отрезке
[
)
ba, каждая из функций
()
xf
и
()
x
ϕ
удовлетворяет условиям определения 5 и условию:
() ()
xxf
ϕ
≤≤0 . Тогда
1) из сходимости
()
∫
b
a
dxx
ϕ
следует сходимость интеграла
()
∫
b
a
dxxf
;
2) из расходимости
()
∫
b
a
dxxf следует расходимость ин-
теграла
()
∫
b
a
dxx
ϕ
.
Теорема 4. Пусть на отрезке
[
)
ba, функция
(
)
xf удовле-
творяет условиям определения 5. Тогда из сходимости инте-
грала
()
∫
b
a
dxxf следует сходимость интеграла
()
∫
b
a
dxxf .
В этом случае интеграл
()
∫
b
a
dxxf называется абсолютно
сходящимся.
Замечание 7. Аналогичные теоремы справедливы для
функций, удовлетворяющих определению 6.
Замечание 8. В качестве функций, с которыми удобно
сравнивать функции, стоящие под знаком несобственного инте-
грала, часто берут
()
α
xс −
1
. Легко проверить, что
()
∫
−
c
a
xс
dx
α
сходится при
1
<
α
, расходится при 1≥
α
. Это же относится и
к интегралам
()
∫
−
c
a
ax
dx
α
.
129
Пример 13.
∫
−
1
0
3
1 x
xdx
.
◄ Подынтегральная функция имеет разрыв в точке
1
=
x
на промежутке
[
)
1,0 . Справедливы следующие неравенства:
x
x
x
xxx
−
<
−
<<
1
1
1
,,1
3
3
.
Интеграл
∫
−
1
0
1 x
dx
сходится (по замеч. 8 при 1
2
1
<=
α
).
Тогда по теореме 3 сходится и интеграл
∫
−
1
0
3
1 x
xdx
.►
10.5. Значения некоторых несобственных интегралов
Гамма–функция
)(x
Γ
:
∫
+∞
−−
=
0
1
)( dttex
xt
Γ
– сходится при
0>x
,
0;)( >x
Γ
)()1( xxx
Γ
Γ
=
+
при 0>x ,
π=
⎟
⎠
⎞
⎜
⎝
⎛
2
1
Γ
;
(
)
11
=
Γ
;
∈
=
+
nnn ,!)1(
Γ
N
,
∫
=
1
0
2
1
dx
x
,
∫
π
=
−
1
0
2
2
1
1
dx
x
,
∫
+∞
=
1
2
1
1
dx
x
,
∫
+∞
∞−
π=
+
dx
x
2
1
1
,
∫
+∞
−
>
π
=
0
0,
2
22
a
a
dxe
xa
,
∫
+∞
>
π
=
0
0,
2
sin
adx
x
ax
,
∫
+∞
−
>
+
=
0
22
0,sin a
na
n
nxdxe
ax
.

130
ГЛАВА 3. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
(ФНП)
§ 1. Понятие ФНП. Элементы топологии в
n
R
Представление о функции нескольких переменных могут
дать простые примеры. Площадь прямоугольника
yxS
⋅
=
.
Если длины сторон
x
и рассматривать как независимые пе-
ременные, то – функция этих переменных. Площадь тре-
угольника
y
S
ϕ= sin
2
1
xyS (
x
и – стороны треугольника, y
ϕ
–
угол между ними) можно рассматривать как функцию трех не-
зависимых переменных.
Рассмотрим некоторое множество точек
D из плоскости
R
R
×=
2
R
, и если каждой точке D
M
∈ , имеющей координаты
),( yx , в силу некоторого закона приведено в соответствие
число , то говорят, что на множестве
f
z D задана функция двух
переменных
).,( yxfz
=
Множество D называется областью
определения
функции
),( yxf
.
Функцию ),( yxfz
=
от двух переменных можно изобра-
зить в трехмерном пространстве, где задана прямоугольная де-
картова система координат
OXYZ в виде геометрического места
точек , а область определения – на плоскости
)),(,,( yxfyx
.
XOY
Пример 1. Геометрическим местом точек для функции
22
1 yxz −−= является верхняя половина шаровой поверх-
ности (рис. 3). Область определения находится, исходя из усло-
вия неотрицательности подкоренного выражения (рис. 4):
{
}
1:),(
22
≤+= yxyxD
(если граница области не включается, то изображается пунк-
тирной линией).
