Бухенский К.В., Елкина Н.В., Лукьянова Г.С. Опорные конспекты по высшей математике. Часть 3
Подождите немного. Документ загружается.

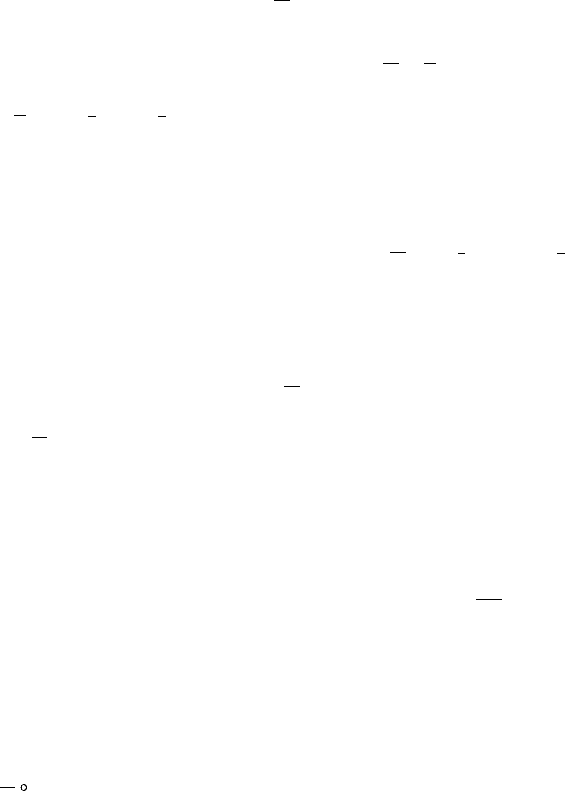
71
Работа переменной силы
( ) ( )( )
yxQyxPF ,,,
по переме-
щению материальной точки по кривой
L
равна:
( ) ( )
∫
⋅=
∫
+=
LL
dFdyyxQdxyxPA ,,
,
где
jdyidxd ⋅+⋅=
. В этом состоит физический смысл КИ
2-го рода.
Другие применения КИ 2-го рода будут рассмотрены в гла-
ве 4.
2.9. Примеры решения задач
Пример 1. Найти работу силового поля
( )
jyxixyF ++=
по перемещению материальной точки по параболе
2
xy =
от
начала координат до точки
( )
1,1M
.
◄ Для нахождения работы используем формулу
( ) ( )
∫
+=
L
dyyxQdxyxPA ,,
, где
( ) ( )( )
yxQyxPF ,,,
. В данном
случае
( )( )
yxxyF +,
, т.е.
( )
xyyxP =,
,
( )
yxyxQ +=,
.
Кривая
2
: xyL =
,
[ ] [ ]
1;0; =∈
MO
xxx
задана явно, поэто-
му
dxxdxydy 2=
′
=
. Тогда от КИ 2-го рода можно перейти к
определенному интегралу:
( )
( )( )
12
17
2
1
0
22
=
∫
⋅++⋅=
∫
++= dxxxxxxdyyxdxxyA
L
. ►
Пример 2. Найти площадь фигуры, ограниченной кардиои-
дой
−=
−=
,2sinsin2
,2coscos2
:
tty
ttx
L
где
π
20 ≤≤ t
.
◄ Для нахождения площади воспользуемся формулой
∫
−=
L
dxydyxS
2
1
, при этом учтем, что кривая
L
задана пара-
метрически. Тогда:
( )
dtttdtydy 2cos2cos2 −=
′
=
и
( )
dtttdtxdx 2sin2sin2 +−=
′
=
. Преобразуем подынтеграль-
ное выражение:
( ) ( )
−−⋅−=− dtttttdxydyx 2cos2cos22coscos2

72
( ) ( ) ( )
dttdttttt cos162sin2sin22sinsin2 −=+−⋅−−
.
Найдем искомую площадь:
( )
π
π
6cos16
2
1
2
1
2
0
=
∫
−=
∫
−= dttdxydyxS
L
. ►
Пример 3. Найти объем тора, полученного вращением ок-
ружности
( )
12
2
2
=−+ yx
вокруг оси
OX
.
◄ Искомый объем найдем по формуле
∫
=
L
OX
dyxyV
π
2
.
Данную окружность удобнее задать параметрически:
( )
=−
=
⇒=
−+
,sin2
,cos
12
2
2
ty
tx
yx
π
20 ≤≤ t
.
Тогда искомый объем равен:
( ) ( )
2
2
0
4sin2sin2cos22
πππ
π
=
∫
′
+⋅+⋅=
∫
= dttttdyxyV
L
OX
. ►
Пример 4. Проверить, что КИ 2-го рода не зависит от пути
интегрирования, и вычислить его:
( ) ( )
( )
( )
∫
+++=
0;2
1;1
3222
4663 dyyyxdxxyxI
.
◄ В данном КИ
( )
22
63, xyxyxP +=
,
( )
32
46, yyxyxQ +=
.
Проверим выполнимость условий теоремы 4:
xy
x
y
QP
xyxyQ
xyyxP
′
=
′
⇒
=⋅=
′
=⋅=
′
1226
1226
,
т.е. заданный КИ 2-го рода не зависит от пути интегрирования.
1-й способ. Вычислим заданный КИ 2-го рода по отрезку
AB
, где
( )
1;1A
,
( )
0;2B
(рис. 6).
O
Y
X
1
1
A
B
2
C
Рис. 6

73
Прямую
AB
можно задать через две данные точки:
⇒
−
−
=
−
−
⇒
−
−
=
−
−
10
1
12
1
:
yx
yy
yy
xx
xx
AB
AB
A
AB
A
[ ]
.2;1,2: ∈−=⇒ xxyAB
Тогда от заданного КИ 2-го рода можно перейти к опреде-
ленному интегралу в силу того, что отрезок
AB
задан явно:
( ) ( ) ( )
( )
( )
322426263
2
1
3
2
2
2
=
∫
′
−⋅−+−⋅+−⋅+= dxxxxxxxxI
.
2-й способ. Вычислим заданный КИ 2-го рода по ломаной
ACB
, звенья которой параллельны осям координат (рис.6). То-
гда
∫
+
∫
=
∫
CBACACB
.
[ ]
0;1,1: ∈= y
xAC
, поэтому
00 =⋅=
′
= dydyxdx
. Тогда:
( )
[ ]
∫
−=+⋅+⋅⋅+⋅=
∫
0
1
3222
441601613 dyyyy
AC
.
[ ]
2;1,0: ∈= xyCB
, поэтому
00 =⋅=
′
= dxdxydy
. Тогда:
( )
[ ]
700406063
2
1
322
=
∫
⋅⋅+⋅+⋅+=
∫
dxxxx
CB
.
Окончательно
374 =+−=
∫
+
∫
=
∫
CBACACB
. ►
Пример 5. Восстановить функцию по ее полному диффе-
ренциалу:
( )
( )
2
2
yx
dyydxyx
dU
+
++
=
.
◄ Если обозначить
( )
( )
2
2
,
yx
yx
yxP
+
+
=
и
( )
( )
2
,
yx
y
yxQ
+
=
,
то
dyQdxPdU +=
. Тогда искомую функцию можно найти по
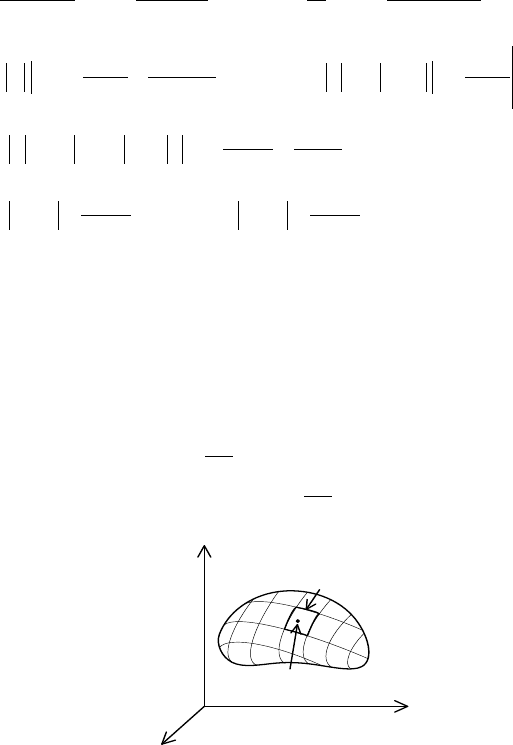
формуле
( ) ( ) ( )
CdxQdyPyxU
y
y
x
x
+
∫
+
∫
=
00
,,,
0
γγχχ
, где в каче-
74
стве точки
( )
00
, yx
возьмем
( )
0,1
. Точку
( )
0,0
брать нельзя,
т.к. в ней не существуют функции
( )
yxP ,
и
( )
yxQ ,
. Получим:
( ) ( ) ( )
=+
∫
+
∫
= CdxQdPyxU
y
x
01
,0,,
γγχχ
( )
( )
( )
( )
=+
∫
+
−+
+
∫
=+
∫
+
+
∫
+
⋅+
= Cd
x
xx
dCd
x
d
y
x
y
x
0
2
10
2
1
2
1
0
02
γ
γ
γ
χ
χ
γ
γ
γ
χ
χ
χ
( )
=+
+
+++=+
∫
+
−
+
+= C
x
x
xxCd
x
x
x
y
y
y
x
0
0
0
2
1
lnln
1
ln
γ
γγ
γ
γ
χ
( )
=+
+
−
+
+−++= C
x
x
yx
x
xyxx
0
lnlnln
C
yx
x
yxC
yx
x
yx
~
ln1ln +
+
++=+−
+
++=
, где
1
~
−=
CC
. ►
§ 3. Поверхностный интеграл (ПИ) 1-го рода
3.1. Понятие ПИ 1-го рода
Пусть на некоторой поверхности
S
пространства
OXYZ
задана непрерывная функция
( )
zyxfu ,,=
.
Разобьем поверхность
S
на
n
частей
1
S
,…,
n
S
, не имею-
щих общих внутренних точек, площади которых равны
i
S
∆
, а
диаметры равны
i
d
,
ni ,1=
. На каждой части
i
S
выберем про-
извольную точку
( )
iiii
zyxM ,,
,
ni ,1=
(рис. 7).
X
Y
O
Z
S
i
M
i
S
Рис.7
75
Опр. 1. Интегральной суммой 1-го рода называется выра-
жение вида
( )
∑
⋅
=
n
i
iiii
Szyxf
1
,,
∆
.
При увеличении числа частей разбиения (
∞→n
) потребу-
ем, чтобы максимальный диаметр этих частей стремился к ну-
лю, т.е.
0max
1
→=
≤≤ ni
i
dd
.
Опр. 2. Поверхностным интегралом (ПИ) 1-го рода от
функции
( )
zyxfu ,,=
по поверхности
S
называют предел ин-
тегральных сумм 1-го рода при
0→d
(
∞→n
), если он не за-
висит ни от способа разбиения поверхности
S
на части, ни от
выбора точек на них:
( ) ( )
∫∫
=
∑
⋅
=
→
∞→
S
n
i
iiii
d
n
dSzyxfSzyxf ,,,,lim
1
0
∆
.
Теорема. Если поверхность
S
гладкая, а функция
( )
zyxfu ,,=
непрерывная на
S
, то ПИ 1-го рода
( )
∫∫
S
dSzyxf ,,
существует.
3.2. Свойства ПИ 1-го рода
1.
( ) ( )
∫∫
⋅=
∫∫
⋅
SS
dSzyxfCdSzyxfC ,,,,
, где
constC =
.
2.
( ) ( )( ) ( ) ( )
∫∫
+
∫∫
=
∫∫
+
SSS
dSzyxgdSzyxfdSzyxgzyxf ,,,,,,,,
.
3.
( ) ( ) ( )
∫∫
+
∫∫
=
∫∫
21
,,,,,,
SSS
dSzyxfdSzyxfdSzyxf
,
где
21
SSS =
, а
21
SS
состоит из общей для них границы.
4.
Π
Π
SdS =
∫∫
, где
Π
S
– площадь поверхности
Π
.
3.3. Вычисление ПИ 1-го рода
Вычисление ПИ 1-го рода по поверхности
S
сводится к
вычислению двойного интеграла по области
XY
D
– проекции
S
на плоскость
XOY
, все зависит от способа задания
S
.
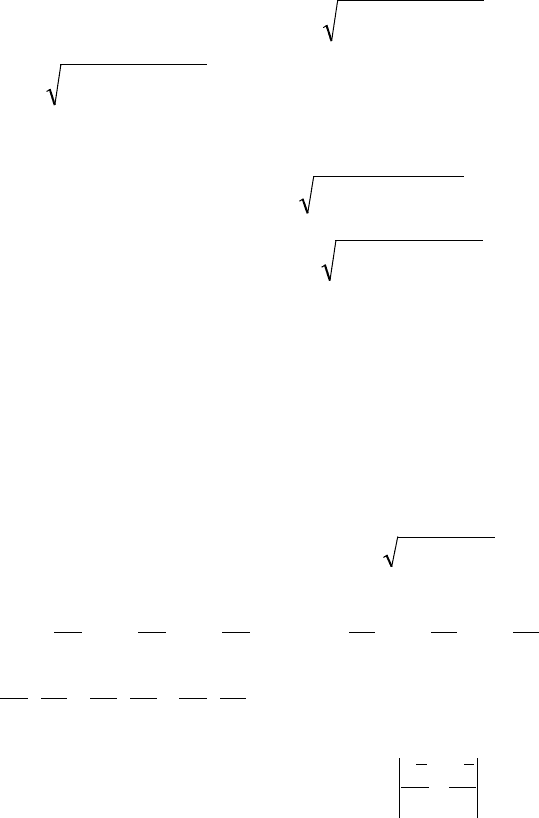
76
Явное задание поверхности
S
:
( )
yxzz ,=
,
( )
XY
Dyx ∈,
.
Если эта функция непрерывна вместе со своими частными про-
изводными
x
z
′
и
y
z
′
, ПИ 1-го рода сводится к ДИ так:
( ) ( )( ) ( )
( )
∫∫
′
+
′
+⋅=
∫∫
XY
D
yx
S
dydxzzyxzyxfdSzyxf
22
1,,,,,
,
где
( )
( )
22
1
yx
zzdS
′
+
′
+=
– дифференциал элемента площади.
Аналогичные формулы верны, если поверхность
S
задана
уравнением
( )
zxyy ,=
или
( )
zy
xx ,=
:
( ) ( )( ) ( ) ( )
∫∫
′
+
′
+⋅=
∫∫
XZ
D
zx
S
dzdxyyzzxyxfdSzyxf
22
1,,,,,
или
( ) ( )( )
( )
( )
∫∫
′
+
′
+⋅=
∫∫
YZ
D
zy
S
dzdyxxzyzyxfdSzyxf
22
1,,,,,
,
где
XZ
D
и
YZ
D
– проекции
S
на плоскости
XOZ
и
YOZ
со-
ответственно.
Параметрическое задание поверхности
S
:
( )
( )
( )
=
=
=
,,
,,
,,
vuzz
vuyy
vuxx
где
( )
vux ,
,
( )
vuy ,
,
( )
vuz ,
– непрерывно дифференцируемые
функции в области
G
плоскости
UOV
. Тогда:
( ) ( ) ( ) ( )( )
∫∫
−⋅⋅=
∫∫
GS
dvduBCAvuzvuyvuxfdSzyxf
2
,,,,,,,
,
где
222
∂
∂
+
∂
∂
+
∂
∂
=
u
z
u
y
u
x
A
,
222
∂
∂
+
∂
∂
+
∂
∂
=
v
z
v
y
v
x
C
,
v
z
u
z
v
y
u
y
v
x
u
x
B
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
=
.
Иногда последнюю формулу записывают в векторном виде:
( ) ( ) ( ) ( )( )
∫∫
∂
∂
×
∂
∂
⋅=
∫∫
GS
dvdu
v
r
u
r
vuzvuyvuxfdSzyxf ,,,,,,,
,

77
где
v
r
u
r
∂
∂
×
∂
∂
– модуль векторного произведения векторов
k
u
z
j
u
y
i
u
x
u
r
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
и
k
v
z
j
v
y
i
v
x
v
r
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
.
3.4. Приложения ПИ 1-го рода
Площадь поверхности
Π
, заданной в пространстве
OXYZ
, равна (по свойству 4):
∫∫
=
Π
Π
dSS
.
Масса поверхности
S
с поверхностной плотностью веще-
ства
( )
zyx ,,
µ
вычисляется по формуле:
( )
∫∫
=
S
S
dSzyxm ,,
µ
.
Статические моменты поверхности
S
с поверхностной
плотностью вещества
( )
zyx ,,
µ
относительно координатных
плоскостей
XOY
,
XOZ
,
YOZ
соответственно вычисляются по
формулам:
( )
∫∫
⋅=
S
XY
dSzyxzM ,,
µ
,
( )
∫∫
⋅=
S
XZ
dSzyxyM ,,
µ
,
( )
∫∫
⋅=
S
YZ
dSzyxxM ,,
µ
.
Координаты центра масс поверхности
S
с массой
S
m
и
статическими моментами
XY
M
,
XZ
M
,
YZ
M
могут быть вычис-
лены по формулам:
S
YZ
c
m
M
x =
,
S
XZ
c
m
M
y =
,
S
XY
c
m
M
z =
.
Моменты инерции поверхности
S
с заданной поверхно-
стной плотностью
( )
zyx ,,
µ
относительно координатных плос-
костей
XOY
,
XOZ
,
YOZ
соответственно вычисляются по
формулам:
( )
∫∫
⋅=
S
XY
dSzyxzJ ,,
2
µ
,
( )
∫∫
⋅=
S
XZ
dSzyxyJ ,,
2
µ
,
78
( )
∫∫
⋅=
S
YZ
dSzyxxJ ,,
2
µ
.
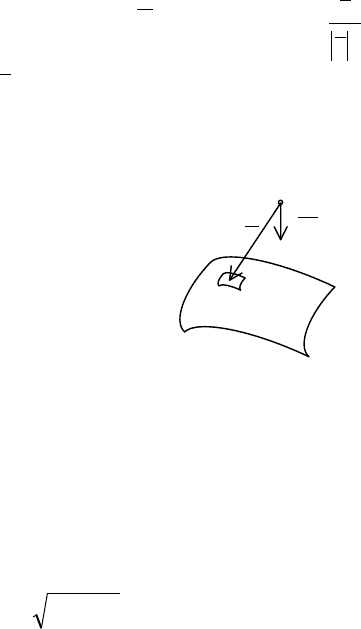
Сила притяжения между поверхностью
S
с заданной по-
верхностной плотностью
( )
zyx ,,
µ
и телом массой
m
, находя-
щимся в точке
( )
Szyx ∉
000
,,
, определяется выражением:
( )
∫∫
⋅=
S
dS
r
r
zyxGmF
3
,,
µ
,
где
( )
000
,, zzyyxxr −−−
– радиус-вектор произвольной точки
поверхности
S
,
21311
скгм10673,6
−−−
⋅⋅=G
– гравитационная
постоянная (рис.8).
dS
m
F
r
S
Рис. 8
Полный заряд поверхности
S
с поверхностной плотно-
стью распределения заряда
( )
zyxq
,,
выражается формулой:
( )
∫∫
=
S
dSzyxqQ ,,
.
3.5. Примеры решения задач
Пример 1. Найти момент инерции однородной поверхности
конуса
2
22
≤≤+ zyx
относительно плоскости
XOY
.
◄ Т.к. заданная поверхность
S
является однородной, то ее
поверхностная плотность
( )
1,, =zyx
µ
, поэтому для нахожде-
ния искомого момента инерции используем формулу
∫∫
=
S
XY
dSzJ
2
.
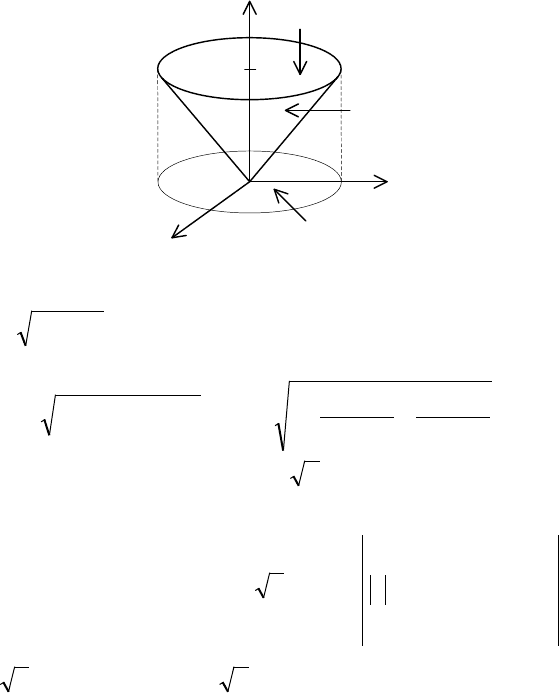
79
Полная поверхность конуса состоит из боковой поверхно-
сти и поверхности основания:
оснбок
SSS =
(рис. 9), значит,
∫∫
+
∫∫
=
∫∫
оснбок
SSS
, т.е.
оснбокXY
IIJ
+=
.
X
Y
O
Z
S
осн
S
бок
D
xy
2
2
2
Рис. 9
Боковая поверхность конуса задана функцией
22
yxz +=
. Поэтому дифференциал элемента площади мож-
но найти так:
( )
( )
⇒
+
+
+
+=
′
+
′
+= dydx
yx
y
yx
x
dydxzzdS
yx
22
2
22
2
22
11
dydxdS 2=⇒
.
Тогда можно вычислить интеграл
бок
I
:
( )
=
≤≤
≤≤=
=+
=
∫∫
⋅+=
∫∫
=
πϕ
ρρ
ρ
20
20,
:
2
222
222
I
yxПСК
dydxyxdSzI
XYбок
DS
бок
πρρρϕ
π
282
2
0
2
2
0
=
∫
⋅
∫
⋅= dd
.
Поверхность основания конуса задается функцией
2=z
,
поэтому вычислим интеграл
осн
I
:
80
ππ
164442
222
=⋅=⋅=
∫∫
=
∫∫
=
∫∫
=
осносн
SSS
осн
RSdSdSdSzI
осносносн
.
В итоге найдем искомый момент инерции:
( )
228 +=+=
π
оснбокXY
IIJ
. ►
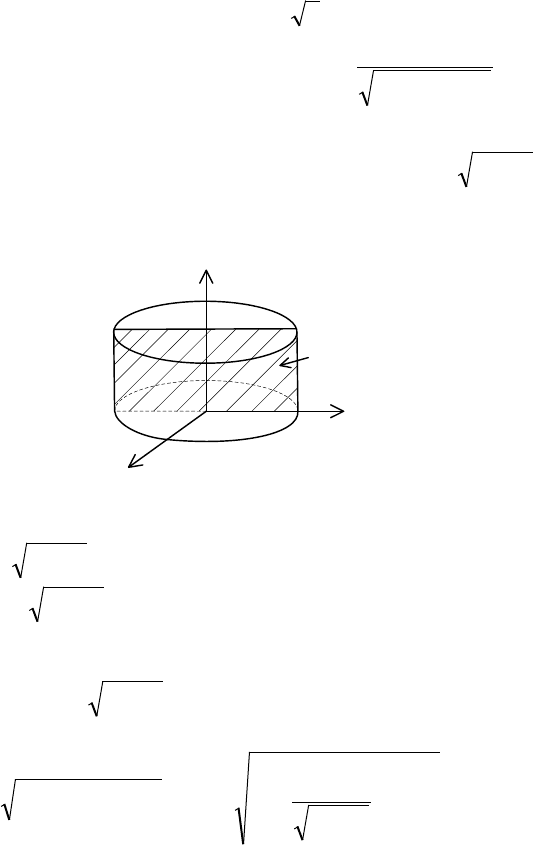
Пример 2. Вычислить интеграл
∫∫
++
=
S
zyx
dS
I
222
, где
S
– часть поверхности цилиндра
9
22
=+ yx
,
20 ≤≤ z
.
◄ 1-й способ. Зададим поверхность
S
явно:
2
9 yx −±=
,
20 ≤≤ z
. Тогда она может быть спроектирована на плоскость
YOZ
в область
YZ
D
, в которой
33 ≤≤− y
,
20 ≤≤ z
(рис. 10).
X
Y
O
Z
D
yz
3
3
2
Рис. 10
Т.к. поверхность
S
состоит из двух частей
2
1
9: yxS −=
(передняя поверхность цилиндра) и
2
2
9: yxS −−=
(задняя поверхность), то воспользуемся
свойством 3 ПИ 1-го рода и найдем интегралы по каждой из
частей, а затем результаты сложим.
Если
2
9 yx −±=
, то найдем дифференциал элемента
площади:
( )
( )
⇒+
−
+=
′
+
′
+= dzdy
y
y
dzdyxxdS
zy
2
2
2
22
0
9
11
