Будко В.Н. Сборник описаний задач специального лабораторного практикума Компьютерный эксперимент темы 3, 4, 5

Подождите немного. Документ загружается.

Министерство общего образования

Российской федирации

Воронежский государственный университет

Физический факультет

Кафедра информационных систем

Сборник

описаний задач специального лабораторного практикума.

"компьютерный эксперимент".

Темы 3,4,5.

для студентов 4-го курса д /о

Физического факультета

кафедры информационных систем

Составитель:

Будко В .Н .

Воронеж 2000

Введение .

В современной науке и технике все большую роль приобретает численный эксперимент -

моделирование на ЭВМ физических процессов.ЭВМ оснащены средствами визуализации

результатов, дают возможность проедставить решение задачи на графическом дисплее в

наглядной динамической форме , наблюдать зависимость решения от параметров.Все это

позволяет приблизить численный эксперимент к натурному.Моделирование физического

эксперимента учит "чувствовать" характер /физичность/ решения уравнений, описывающих

исследуемый объект, развивает интуицию.Существенно , что численный эксперимент зачастую

позволяет предсказать ранее не наблюдавшиеся эффекты и исследовать системы,

недоступные для натурного эксперимента .

Лабораторные работы на данную тему посвящены изучению методик моделирования на ЭВМ

свойств физического объекта и процессов в нем протекающих,как при разовом отклонении от

равновесного состояния ,так и при непрерывном произвольном внешнем воздействии.

Основные этапы численного эксперимента .

Подготовительный этап:

--Постановка задачи : формулирование системы уравнений с граничными и начальными

условиями ,переход к безразмерным переменным и функциям,выделение варьируемых

параметров,выбор характерных масштабов /т.к. числа,с которыми оперирует ЭВМ заключены в

конечном интервале /.

--Выбор метода решения и построение расчетного алгоритма.

--Составление и отладка программы.

--Основной этап-собственно численный эксперимент.

--Фиксируются все параметры задачи , кроме одного , который иподвергается изменению

/варьированию/ в разумном интервале .

--Рассчитывается необходимое число вариантов.

--Производится теорический анализ полученной информации.

--Корректируются и проводятся, если необходимо повторные эксперименты , т.е . модель

уточняется.

--На базе полученных данных осуществляется поиск искомых закономерностей, описывающих

объект.

--Результаты численного эксперимента сопоставляются с натурными данными .

Учебная цель работ : изучение приципов компьютерного эксперимента и областей его

применения, изучение общей методики подхода к построению иммитационной модели сложной

системы произвольного физического объекта . Практическое проведение машинного

эксперимента для простых физических объектов.

Научная цель работ : составление комплекса модулей /подпрограмм/ для програмного

моделирования.

• 3.Стахастическое моделирование .

Стахастическая модель реального ,как детерменированного так и вероятностного объеата – это

такая модель, результаты мспытаний которой имеют статистический характер , т.е . могут быть

представленны в виде вероятности изучаемого события или средними значениями его

характеристик. Такое моделирование основано на применении метода статистических

испытаний, являющегося численным способом решения задачи при помощи использования

случайных величин. Этот метод называют еще методом Монте - Карло [12] по имени города

известного своими игорными домами . Название метода напоминает о том, что простейшим

прибором для получения случайной величины является рулетка .

Общая идея задач методом Монте - Карло заключается в следующем :

1.Выбираются по жребию /датчику случайных чисел/ значения параметров исследуемой

системы и параметров входных воздействий на нее /назовем их входными параметрами

модели системы/.

2.Воспроизводится процесс функционирования этой системы при выбранном значении

входных параметров ее модели и определяются реакции системы, т.е . выходные параметры ее

модели . При этом, как входные , так и выходные параметры модели рассматриваются как

детерминироавнные .Такое однократное воспроизведение функционирования объекта и

называют статистическим испытанием.

3.После многократного повторения статистических испытаний полученные результаты

подвергаются статистической обработке с целью представления их в виде статистических

характеристик : вероятности появления изучаемого события, средних значений параметров,

возможных отклонений параметров от средних значений и др.

Достоинства метода статистических исытаний.

- простая структура вычислительного алгоритма ;

- наглядная вероятностная трактовка модели ;

- малочувствительность к отдельным ошибкам вычислений ;

- простота оценки точности полученных результатов ;

Недостатки :

- необходимость знания закона распределения случайных значений параметров

объекта и построение в статистической модели адекватного датчика случайных чисел

;

- необходимость большого количества статистических испытаний для получения

приемлимой точности результата .

Ошибка конечного результата , как правило , пропорциональна

Где : D – константа , зависящая от алгоритма решения задачи ,

N – число испытаний.

Следовательно , чтобы уменьшить ошибку в 10 раз надо увеличить объем испытаний в 100 раз.

Метод Монте - Карло позволяет моделировать любые процессы, на протекание которых

влияют случайные факторы. Но для многих задач, не связанных с какими либо случайностями ,

можно искусственно придумать вероятностную модель /и даже не одну/, позволяющую решать

эти задачи .

Поэтому можно говорить о методе Монте - Карло как об универсальном методе решения как

математических задач, так и задач моделирования физических объектов. Однако , практическая

эффективная реализация метода Монте - Карло возможна только на ЭВМ .

Общая схема метода Монте - Карло .

Пусть требуется вычислить некоторую величину «А». Придумаем такую случайную величину

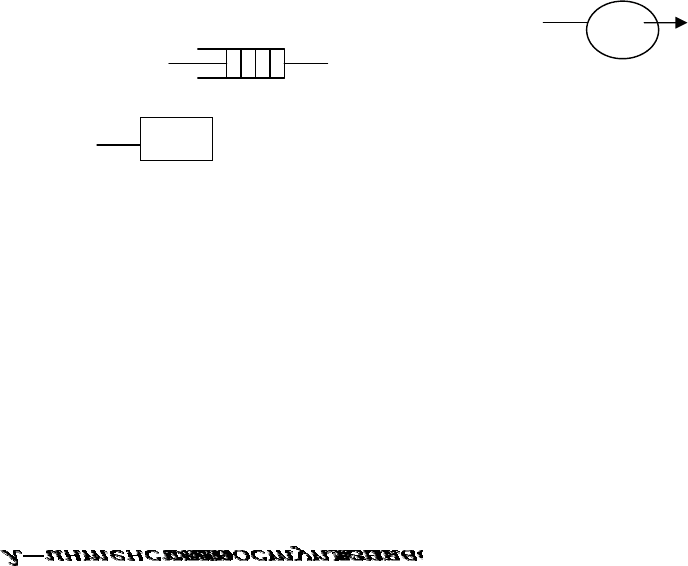
чтобы матожидание ее равнялось бы «А». Например, требуется определить площадь

произвольно заданной графически или аналитически плоской фигуры «А», рис.1.

Изменим масштаб так, чтобы эта фигура попала внутрь единичного квадрата . Выберем в

квадрате N случайных точек /по датчику случайных чисел, равномерно распеделенных на

отрезке [0,1]. Подсчитаем из них число точек N*, попавших внутрь области «А». Тогда

геометрически очевидно , что искомая площадь приблизительно равна отношению N*/N. При

этом чем больше будет N, тем точнее результат.

Y 1

Рис.1.

1 X

Примеры статистических моделей.

3.1Расчет качества изделия.

Например, возьмем электронное устройство . Пусть качество этого изделия определяется

входным параметром «К» , которое можно вычислить как функцию от величин его элементов,

например, R, L, C : k=f(R1,R2,… ,C1,C2,… ,L1,L2,… ) (1)

Задача – оценить как повлияют отклонения величин всех элементов от наминальных значений

на величину «К» . Можно оценить пределы изменения «К» , выбирая для всех элементов

«худшие» значения. Но при сложной функции (1) трудно понять какой набор значений

элементов будет наихудшим. Кроме того , когда элементов много оценка окажется существенно

завышенной, ибо маловероятно , чтобы на самом деле все элементы были худшими . Поэтому

считаем параметры всех элементов и саму величину «К» случайными и найдем статистические

характеристики «К» . Определить аналитически распределение «К» для вычисления

матожидания, дисперсии и других стат.характеристик «К» для мало -мальски сложной функции

(1) невозможно .

Применим метод Монте - Карло .

---- задаем функции распределения для величин всех элементов и на их базе моделируем

датчики случайных значений для каждого элемента .

---- для каждого элемента разыгрывается значение его параметра.

---- по формуле (1) вычисляется значение «К» .

---- повторив этот вычислительный опыт N раз получим вариационный ряд значений : К1, К2,

К3,… ,КN

---- из этого ряда можно определить :

- функцию распределения (гистограмму) для «К» ,

- доверительные интервалы для «К» ,

- матожидание и дисперсию «К» ,

и другие характеристики .

3.2 Имитационные модели массового обслуживания.

Такие задачи как исследование работы систем связи , работы , например, цеха как объекта

управления, исследование процесса передачи данных в информационно -вычислительных

сетях , исследование характеристик системы комплексного испытания изделий в производстве ,

исследование характеристик доступа к моноканалу локальной сети ЭВМ и др [13] относятся к

классу имитационных моделей массового обслуживания, которые объединяются общим

подходом к методике их решения.

В общем случае такая система состоит из I источников заявок : i =

1,2,3,… I

N накопителей заявок N(n), n = 1,2,3… N и К каналов или пунктов

Обслуживания L = 1,2,… K

Эти элементы объединяются в систему структурной схемой функционирования, называемой –

Q-схемой.

Моделироавние поцесса функционирования системы производится в дискретном времени . Шаг

дискретизации времени в модели определяется из начальных условий постановки задачи

(конкретной).

Заявки в систему поступают в случайные моменты времени . Поток заявок обычно берется

математически простейшим, т.е .задается либо вероятность поступления заявок за шаг

дискретизации времени , либо разыгрывается случайная величина помежутка времени между

двумя последовательностями заявками из закона Пуассона (экспериментального закона

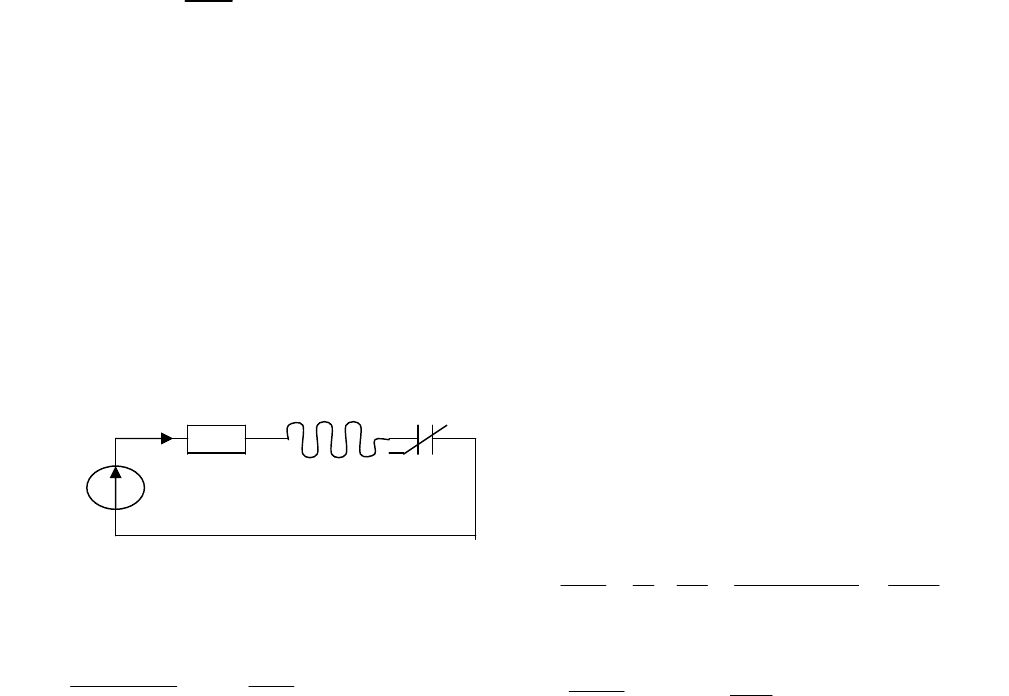
распределения) :

Где t – интервал времени между соседними заявками во времени

Каждая поступающая заявка либо обслуживается немедленно , если есть свободный канал

обслуживания, либо становится на очередь в накопитель, либо делается отказ,если накопитель

переполнен.

Время обслуживания заявки в канале берется либо фиксированным, либо случайным с

заданным законом распределения.

Стат.модель системы массового обслуживания строится, например, для следующих расчетов :

n времени ожидания в очереди среднего времени или распределения,

вероятности об

служивания заявки при заданном времени ожидания,

I(i)

K(L)

λω l ⋅= )( t

n коэффициента простоя каналов, сколько в среднем заявок обслужит система за

заданное время и для расчетов других характеристик.

3.3 Расчет надежности изделия.

Общий подход к решению задач этого класса смотри в [12].

4.Детерминированные модели изменения во времени состояния

параметров физического объекта .

1. Параметры и пере

менные объекта связаны между собой системой обыкновенных

дифференциальных уравнений.

Рассмотрим дифференциальное уравнение 1-го порядка , типа :

К системе таких уравнений, как известно , нетрудно свести и диф .уравнения высших порядков.

Численное решение уравнения (1) при известных начальных условиях x0,y0 заключается в

пошаговом через h =x k+1-xk вычислении нового значения yk+1 по известному

предшествующему yk.

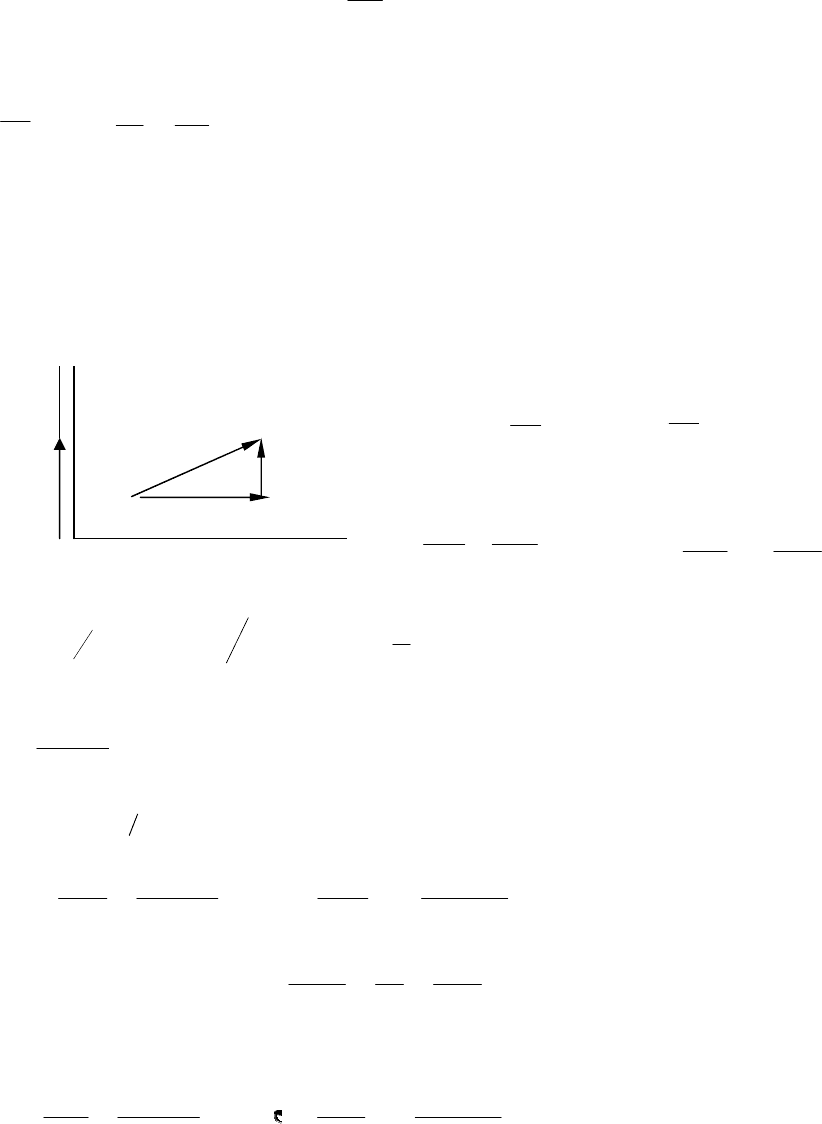
ТЕМА 4.1 Резонанс в колебательном контуре с нелинейной емкостью [1].

Переходя от тока к заряду

получим :

Рассмотрим нелинейный член :

Так как при отсутствии нелинейности должно быть :

а f(q)=q , то представление f(q) степенным полиномом должно иметь вид :

В [1] для упрощения анализа рассматривается апроксимация кусочным полиномом :

),()1( yxf

R L

q U(t)

U=iR+Ldi/dt+Uc

i=dq/dt , Uc=q/c

)(0 qСС

∗

)cos()( 0 tUtU

⋅

∗

qCL

qd )(

)(0

⋅⋅

+∗+

)(

)()(

qCL

⋅=⋅=

⋅⋅

⋅

=ω

)(

1)(

...)(

32 +⋅+⋅+= qbqbqqf

Итак исследуемый объект описывается диф .уравнением 2-го порядка :

Диф .уравнение 2-го порядка можно заменить системой из двух диф .уравнений 1-го порядка

[10],[2] :

Численное решение уравнений (2), (3) можно осуществить как по формулам Эйлера, так и по

формулам Рунге -Кутта [5],[2],[3].

ТЕМА4.2Модель движения заряженной частицы в поле

прямолинейного тока .

Уравнения движения :

V0 Vy0

(X0,y0) Vx0

Для однородного по всей плоскости xy поля равного B0 частица будет двигаться по окружности

с радиусом :

и временем обращения :

Преабразуем уравнения :

введя в них масштаб времени равный

Итак :

3)( qbqqf ⋅+=

)cos(2

...

⋅⋅=⋅++⋅⋅+ ωωα

)2(

iqbqt

⋅−+−⋅⋅= 2)()cos(

0ωω

)3(

,xV

,)( xBVy

dVx

⋅

)( xBVx

dVy

⋅

−=

⋅

0 =

)1(

Vcm

⋅

000 2 Vr ⋅⋅= πτ

)2(

xBq

dVx

⋅⋅

⋅

= ,

mcx

xBq

dVy

⋅

−=

00 2

⋅

dVx

⋅

dVy

⋅

−=

)3(

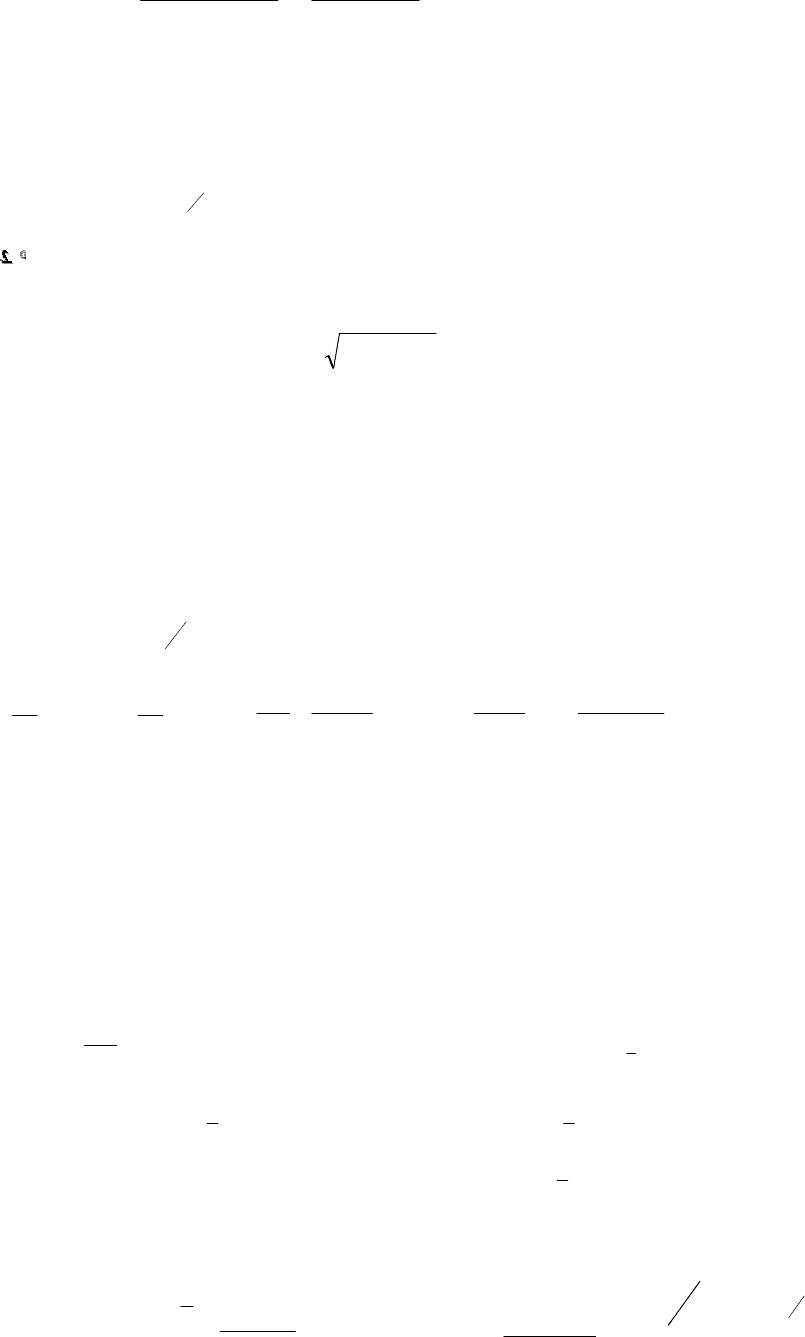
Время обращения

не зависит от начальной скорости V0, поэтому является удобным масштабом времени –

независимым исходным данным моделирования.

В качестве другого исходного данного - масштаба расстояния берём r 0 .По заданным r0 и

находим (см.(3) :

Теперь, так как V0 оказалось косвенно задано через r0 и

нельзя произвольно задавать пару начальных значений проекций скорости Vx и Vy , т.к. они

связаны с V0 соотношением

Поэтому в качестве третьего независимого начального условия берём угол направления

вектора V0.

Итак , исходные данные модели :

мы берём временной шаг модели

По заданным величинам (4) вычисляем :

Итак получим систему уравнений :

Система (5) – нелинейная .

Однако , при достаточно малом шаге интегрирования эту нелинейную систему можно свести к

линейной следующим приёмом. На каждом шаге вычислений нелинейную функцию (в данном

случае C=X0/X ) вычисляем по исходным данным этого шага и считаем для этого шага

константой Сi=X0/Xi .Для следующего шага вычисляем новое значение константы и т. д . Так

здесь для первого шага X=X0.Получаем линейную систему диф .уравнений и по заданным

значениям X0,y0,Vx0,Vy0 находим : X1,y1,Vx1,Vy1 .Теперь берём C1=X0/X1 и на втором шаге по

заданным величинам X1,y1,Vx1,Vy1 находим X2,y2,Vx2,Vy2 и т.д . Для численного решения

системы (5) используем формулы метода Эйлера-Коши, погрешность которого имеет порядок

Отсюда для системы (5) , учитывая, что h=1 получаем :

Система (6) (повезло ) уже яляется решением задачи .

000

qBV

mcV

⋅

)sin(),cos(2 0000,

00 уголVVyуголVVxrV

⋅

0 VyVxV +=

)4(,,,, 00000 вектораVуголryx

самымтемчтоозначаетrвеличинзаданиянормировкивместоВыбор ,, 00

∆

00 2

⋅

,, Vy

dVx

⋅

)5(

mcx

xBq

dVy

⋅

−=

:,),( тоztf

Если =

)]()([)(

)0(

,, 1,1,

)0(

++++++ +⋅ == iii

iiiiii ztfztfzzztfhzz

)6(

1 ][ iiiiiiii VxxxVxVxVxxx ++++++ ==

iii Vyyy

1 ++ =

xcсгдеiiiii VyVyVyVxVx 0

,2 ,)]([

1 =⋅⋅=⋅ +++=+

παααα

αα +⋅

)

(

αα +⋅−

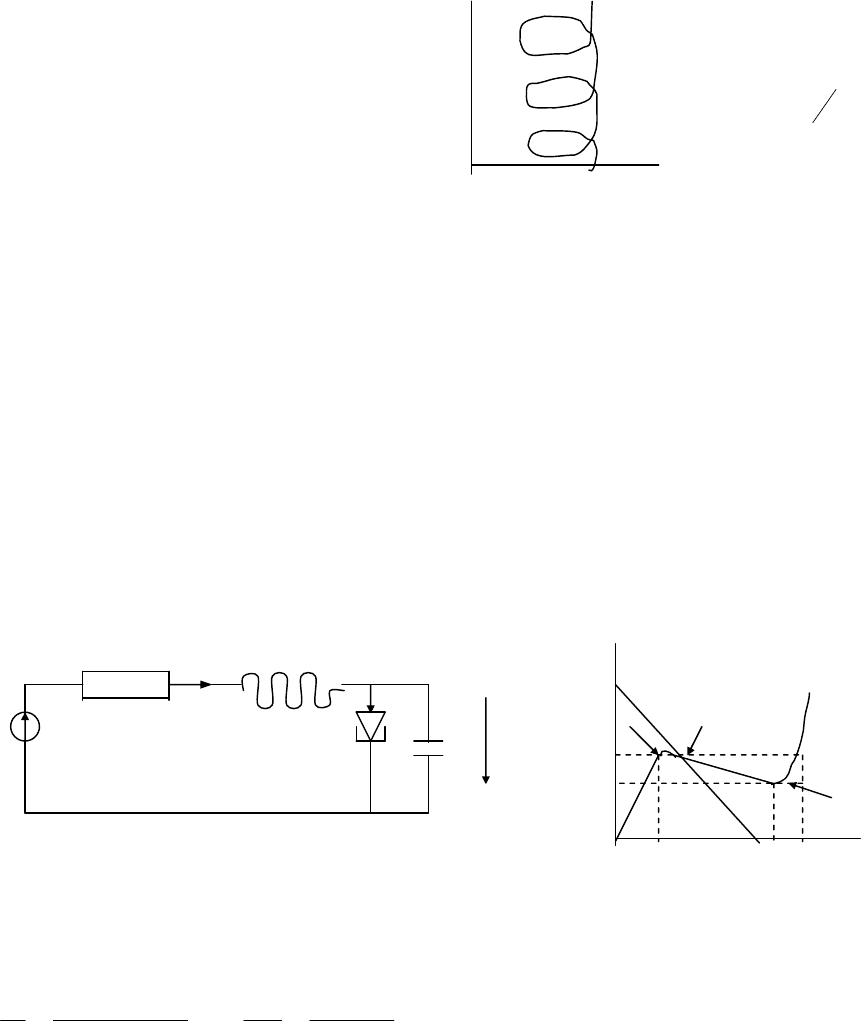
Алгоритм модели :

Ввод t0,r0 печать точки Z1,Z2 на экране

Ввод x0,y0 X:=Z1

X:=x0 y:=Z2

y:=y0 Vx:=Z3

печать точки x,y на графике экрана Vy:=Z4

Ввод «угол» идти «цикл»

Vx=V0*cos(угол) y t0=1000

Vy=V0*sin(угол) r0=10

X0=60

<цикл> C:=X0/X y0=170

qq:=0.5*q*q

Z1:=X+1.5*Vx

Z2:=y+1.5*Vy x

Z3:=Vx+(q+qq)*Vy

Z4:=Vy+(q-qq)*Vx

10 INPUT “t0=”; t0 : INPUT “r0=” ;r0

20 LET V0=2*пi*r0/t0

30 INPUT “x0=” ; x0 :INPUT “y0=” ;y0:LET x=x0 : LET y=y0 : PLOT x,y

40 INPUT “угол=” ;угол

50 LET Vx=V0*cos(угол) : LET Vy=V0*cos(угол)

60 LET C:=X0/X : LET q=2*пi*c/t0 : LET qq=0.5*q*q

70 LET Z1=x+1.5*Vx :LET Z2=y+1.5*Vy

80 LET Z3=Vx+(q+qq)*Vy

90 LET Z4=Vy+(q-qq)*Vx

100 PLOT Z1,Z2

110 LET x=Z1 : LET y=Z2 : LET Vx=Z3 : LET Vy=Z4

130 GOTO 60

ТЕМА4.3Нелинейная автоколебательная система на туннельном диоде.

R L

i I(U) U0/R

+ U A P

- C Im

I2 B

U1 U0 U2 U3

Если выбрать рабочую точку «р» на падающем участке характеристики (участок AB вольт-

амперной характеристики с отрицательным сопротивлением ), то в схеме возникнут автоколебания

и её работа будет описываться диф .уравнениями :

Вольт-амперную характеристику туннельного диода можно апроксимировать либо

экспонециальной зависимостью [2] :

0/0**2:0 trV

0/**2: tCq

−=угол

U 0

)4(

)(

UIi

URiU

di −

−⋅−

)

(

)

(exp(

)

exp(

)

(

−

⋅

−

⋅

≈

где

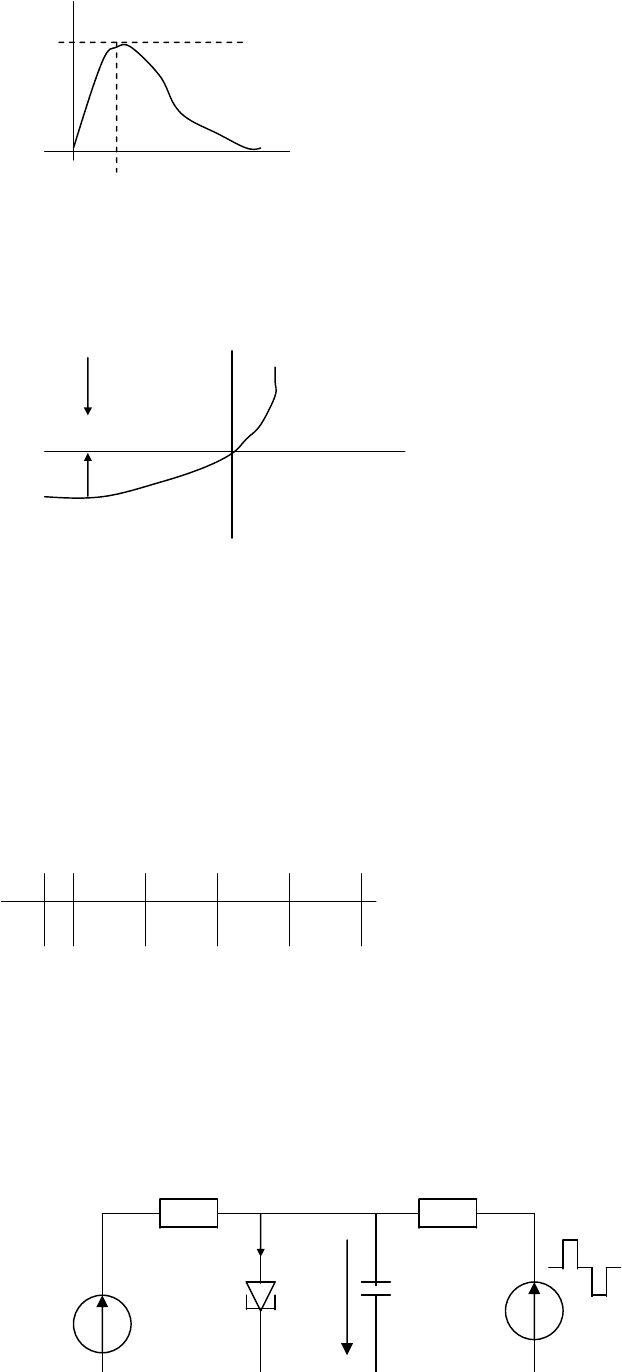
В формуле (5) первый член отображает туннельный эффект p-n перехода,

U1 U

А второй член – есть вольт-амперная характеристика обычного диода (без учёта падения

напряжения на сопротивлении его базы ) с обратным током I0 , поправочным коэффициентом “m” и

тепловым

Типовые параметры туннельного диода :

При такой апроксимации точки (U2,I2) и (U3,Im) не задаются, а получаются как следствие

задаваемых величин (Im,U1) и I0 .Варируя несколько I0 можно приблизительно обеспечить и

апроксимацию желаемой (известной из паспорта диода ) точки (U2,I2).

Либо же вольт-амперную характеристику можно апроксимировать полиномом 5-й степени ,

представленным по схеме Горнера [3] :

I(U)=(((( a5U+a4)U+a3)U+a2)U+a1)U+a0 (6)

где : a0… a5 находятся по пяти точкам графически заданной вольт-амперной характеристикой

туннельного диода. Например, для графика зависимости I(U), построенного по точкам; решая

систему из пяти уравнений

U,B 0 0.2 0.4 0.6 0.8 1.0

I,A 0 0.052 0.023 0.002 0.004 0.013

получим : a0=0, a1=746.333, a2= -3420.833, a3=5734,375, a4= -4168.667, a5=1119.792

Используя прграмму численного решения системы из двух уравнений (4), с учётом (5), можно

вычислить зависимость U(t) и I(t) .

Смотри [В.П .Дьяконов.Справочник по алгоритмам и программам на языке бейсик для

персональных ЭВМ .М .Наука.1987, стр .212].

ТЕМА4.4Триггер на туннельном диоде. [4]

C – паразитная ёмкость ТД и

монтажа.

R1 R2 Uз – сигнал опрокидывания

триггера.

Uп – источник питания.

I U

+ C Uз

Uп

потенциало

BUAA 2.01.001.010Im 1 K

.10101101

0 В UдиапазонРабочийAI <<⋅⋅=

−−

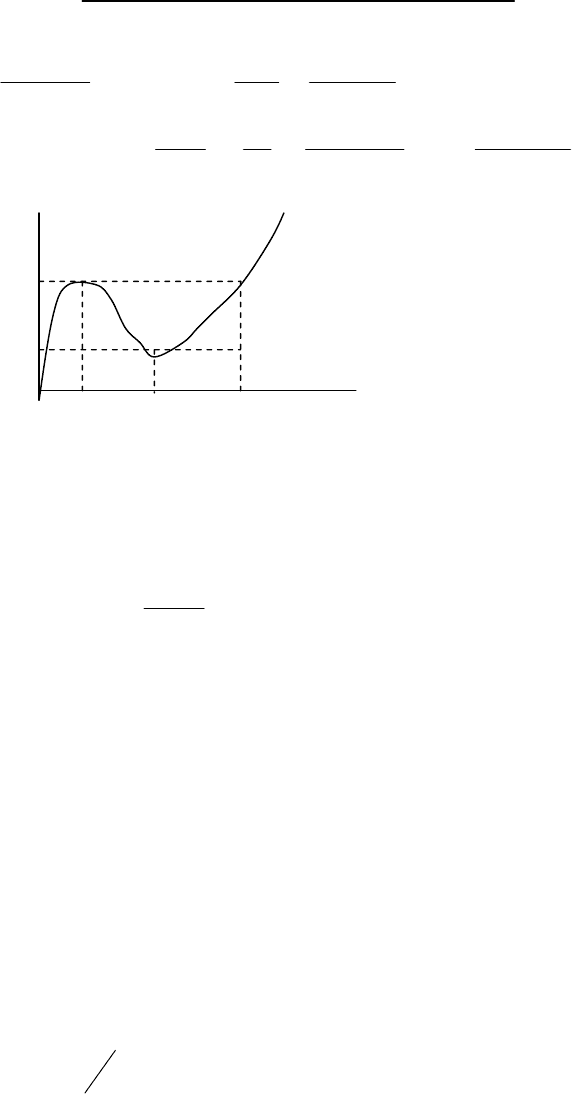
Временные характеристики отображаются уравнениями :

(6)

U1 U2 U3 U

Вольт-амперную характеристику ТД апроксимируем экспонентами :

Задавая три точки (U1,Im), (U2,I2), (U3,Im) и добавляя 4-ое условие , необходимое для

формирования полной системы уравнений с четырьмя неизвестными :

при U=U1.

Для упрощения вычислений примем допущения :

Получим систему уравнений :

Решение этой системы уравнений :

A1=Im*e/U1

e=2.718281828

Для численного решения диф .уравнения (6) с учётом (7) , (8) можно применить любые из

разностных формул Эйлера или Рунге -Кутта .

5.Моделирование объектов, разностные уравнения которых выводятся непосредственно

из

анализа физики процессов в этих объектах .

Примеры.

)(

U зU

Cui

UU п

−

+⋅+=

−













−

−−

−

⋅=

U з U

UU п

Cdt

или

)7()1)(exp()exp()( 221

−

⋅

−

⋅

UAUUAUI

2,,, 121

0)exp()exp()1(

)(

22211 1 =⋅⋅⋅+⋅−⋅⋅−= ⋅ uAuuA

udI

αααα

0)exp()1( 111

⋅

−

⋅

−

⋅ uuA

Im)exp( 1111

⋅

−

⋅

⋅ uuA

0)1)(exp( 122

−

⋅

0)exp( 3131

⋅

−

⋅

uuA

0)exp( 32

⋅

2)exp()exp( 2222121 IuAuuA

⋅

−

⋅

Im)exp( 322

⋅

1 1

=α

)8()/()]/)exp(()/(Im/[ln( 321211222 UUUUUUUI

−

⋅

−

Im)exp( 322

⋅

−