Бруяцкий Е.В., Костин А.Г., Никифорович Е.И., Розумнюк Н.В. Метод численного решения уравнений Навье-Стокса в переменных скорость-давление

Подождите немного. Документ загружается.

ISSN 1561 -9087 Прикладна гiдромеханiка. 2008. Том 10, N 2. С. 13 – 23

УДК 532.526

МЕТОД ЧИСЛЕННОГО РЕШЕНИЯ УРАВНЕНИЙ

НАВЬЕ-СТОКСА В ПЕРЕМЕННЫХ

СКОРОСТЬ–ДАВЛЕНИЕ

Е. В. Б Р У Я Ц К И Й, А. Г. К О С Т И Н, Е. И. Н И К И Ф О Р О В И Ч, Н. В. Р О З У М Н Ю К

Институт гидромеханики НАН Украины, Киев

Получено 12.09.2007

Полная система уравнений Нав ье-Стокса в переменных скорость–давление решается численным методом конечных

разностей для случая вязкой несжимаемой жидкости. Задача формулируется в нестационарной постановке и ре-

шается на установление. Дискретизация исходных уравнений реализуется на разнесенных сетках. Для определения

давления получено эллиптическое уравнение Пуассона путем подстановки выражений для компонентов скорости из

уравнений движения в уравнение неразрывности, подобно МАС-методу. Полученный универсальный дискретный

аналог уравнений Навье-Стокса в виде системы линейных алгебраических уравнений решается итерационным мето-

дом. Эффективность разностной схемы и алгоритм решения тестируются на примере ра счета течения на начальном

участке плоского прямолинейного канала.

Для випадку в’язкої нестисливої рiдини чисельним методом кiнцевих вiдмiнностей вирiшуються повнi рiвняння

Навьє-Стокса у з мiнних швидкiсть–тиск. Задача формулюється в нестацiонарнiй постановцi i розв’язується на вста-

новлення. Для визначення тиску одержано елiптичне рiвняння Пуасона шляхом пiдстановки виразiв для компонент

швидкостi iз рiвнянь руху в рiвняння нерозривностi, подiбно МАС-методу. Дискретизацiя вихiдних рiвнянь реалiзу-

ється на рознесених сiтках. Одержаний унiверсальний дискретний аналог рiвнянь Навьє-Стокса у виглядi системи

лiнiйних алгебраїчних рiвнянь розв’язується iтерацiйним методом. Ефективнiсть вiдмiнної схеми i алгоритму вирi-

шення те стуються на прикладi розрахунку течiї на початковому вiдрiзку плоского прямолiнiйного каналу.

Full Navier-Stokes equations with velocity-pressure variables are solved for viscid incompressible ﬂuid using a ﬁnite di-

ﬀerences method. The problem is set in a non-stationary for mulation and is solved fo r ascer t ainment. To determine

pressure, elliptic Poisson equation is obtained using substitution of expressions for velocity compo nents int o the continui-

ty equation similar to MAC-method. Discretizatio n of initial equations is made on sparsed grids. The obtained universal

discrete analog of Navier-Stokes equations in a form of a system of linear algebraic equations is so lved with an iteration

method. Eﬃciency of the diﬀerences scheme as well as the solution algorithm are tested for a case of ﬂow in an opening

section of a ﬂat rectilinear channel.

ВВЕДЕНИЕ

Изучение течений вязкой несжимаемой жидко-

сти на основе решения полной системы уравне-

ний Навье-Стокса имеют давние традиции. При

этом, в силу сложности определения давления,

разными исследователями исходная система урав-

нений записывалась в двух не противоречащих

друг другу формулировках. В первом варианте

система уравнений записывалась в естественных

физических переменных скорость–давление, а во

втором вариа нте – в переменных вихрь–функция

тока. Су ществует и третий вариа нт решения за-

дач гидромеханики, когда используются перемен-

ные скорость–завихренность.

В литературе известно очень ограниченное чис-

ло случаев, допускающих а налитическое интегри-

рование уравнений Навье-Стокса [2,3,14]. Поэтому

прогресс в этой области возможен лишь за счет

использования численных методов. В настоящее

время для численного решения у равнений Навье-

Стокса существуют и используются несколько де-

сятков разновидно стей разностных схем. Большая

часть из них разработана применительно к систе-

ме уравнений в переменных вихрь –функция тока

[4]. Общим недостатком этого подхода, как изве-

стно, является необходимость использования в том

или ином виде граничного условия для вихря на

твердой поверхности, как, например, условие То-

ма, которое служит условием первого порядка то-

чности относительно шага сетки. Наряду с этим,

использование переменных в их рь-функция то ка

исключает возможность обобщения этого метода

на пространственные и турбулентные потоки. Это

обуславливает повышенный интерес исследовате-

лей к решению уравнений Навье-Стокса в физиче-

ских переменных скорость–давление. Такой под-

ход позволяет решать по единому алгоритму как

двухмерные, так и трехмерные задачи. Однако

этот путь связан с трудностями расчета поля дав-

ления, согласованного с полем скоростей.

Уравнения Навье-Стокса обладают рядом спе-

цифических особенностей, которые существенно

влияют на их численное решение независимо

от формы их записи. Одной из существенных

особенностей является нелинейность и параболо-

эллиптический характер этих уравнений. Поэто-

му, чтобы правильно моделировать эллиптиче-

 Е. В. Бруяцкий, А. Г. Костин, Е. И. Никифорович, Н. В. Розумнюк, 2008 13

ISSN 1561 -9087 Прикладна гiдромеханiка. 2008. Том 10, N 2. С. 13 – 23

скую природу уравнений Навье-Стокса, необходи-

мо использовать эллиптическое уравнение Пуас-

сона для давления. В реальных условиях, при ре-

шении внешних задач обтекания каких-либо тел,

рассматриваемая область может быть и безгра-

ничной, но при численной реализации она моде-

лируется как конечна я, а это осложняет выпол-

нение граничных условий на бесконечности. На-

личие м алого параметра при старшей производ-

ной и нелинейность уравнений Навье-Стокса в со-

четании с их эллиптичностью, при больших чи-

слах Рейнольдса создают условия для образова-

ния в жидкости весьма сложных пространственно-

временных вихревых структур, приводящих к

нестационарности потока жидкости, потери его

устойчивости и переходу к т урбулентному режи-

му течения.

Большинство эффект ивных численных методов

интегрирования уравнений Навье-Стокса осно-

вывается на использовании асимптотического ме-

тода установления, когда для установившихся те-

чений решается нестационарная задача. Основ-

ная сложность получения решения нестационар-

ных уравнений Навье-Стокса, наряду с нелинейно-

стью исходной системы уравнений, связана с тру-

дностью одновременного решения уравнений ко-

личества движения и уравнения неразрывности на

текущем временном шаге.

Один из первых численных методов решения

уравнений Навье-Стокса для несжимаемой ж ид-

кости в естественных физических переменных

скорость–давление был предложен Чориным [5, 6]

и стал известен, как метод "искусственной сжима-

емости". Он основан на том, что в уравнение нера-

зрывности добавляется слагаемое с искусственной

сжимаемостью, которое обращается в нуль, когда

решение устанавливается во времени. Затем были

предложены и другие методы. Среди них отметим

метод "переменных направлений", разработку ко-

торого связы вают с именами Дугласа, Писмана,

Рэчфорда [7, 8]. Успех метода был обязан исполь-

зованию процесса редукции многомерной задачи к

последовательности одномерных задач с трехдиа-

гональными матрицами. Другим, из наиболее ран-

них и получивших широкую известность методов

решения, является предложенный в работах Хар-

лоу [9, 10] метод "маркеров и ячеек"(МАС). Этот

метод в дальнейшем постоянно модифицируется.

Он характерен тем, что исходные уравнения запи-

сываются в переменных скорость–давление, а для

построения конечно-разностной схемы используе-

тся разнесенная сетка [11, 12]. Другая группа ме-

тодов связана с методами расщепления, подробно

рассмотренными в книге Г.И. Марчука [13]. Среди

них от метим метод расщепления по физическим

процессам О.М. Белоцерковского [12]. Далее на

основе идей метода МАС, О.М. Белоцерковским

и Ю.М. Давыдовым б ы л предложен "метод кру-

пных частиц" [14]. Широкое применение в зада-

чах гидродинамики получила одношагова я и дву-

хшаговая схема Лакса-Вендрофа и Мак-Кормака

[15, 16], которая состоит в использовании схемы

"предиктор–корректор". Со временем в ряде ра-

бот была предложена группа методов, получив-

шая название SIMPLE методов. Среди них отме-

тим работы С. Патанкара и П. Сполдинга [17, 18].

Обзор указанных и других методов имеется в ра-

ботах [4, 12 – 14, 17, 18, 20 –28].

В настоящее время, в силу большой практи-

ческой значимости, поиск эффективных разно-

стных схем и алгоритмов решения уравнений дви-

жения вязкой несжимаемой жидкости интенсив-

но продолжается, а оценка их качества определя-

ется сопоставлением результатов расчетов с дру-

гими известными расчетными и эксперименталь-

ными данными.

На современном этапе развития вычислитель-

ной гидромеханики ее дальнейший прогресс свя-

зан с усовершенствованием моделей течения, про-

цессов перемешивания и компьютерных техноло-

гий интегрирования исходных уравнений. После-

дние из них обычно связаны с усложнением вычи-

слительных алгоритмов путем использова ния схем

аппроксимации бо лее высокого порядка точности

и структурированных сеток. Однако этот путь

связан с возрастающей сложностью вычислитель-

ных алгоритмов и программ, который приводит

к большим трудностям их реализации, а потому

доступен лишь некоторым профессионалам. Это

ограничивает возможности их широкого исполь-

зования в проектно-конструкторской деятельно-

сти. Поэтому главная цель нашей работы состоит

в создании и обсуждении относительно простого

численного алгоритма решения фундаментальных

уравнений Навье-Стокса.

1. ОБЩИЙ ПРИНЦИП ПОСТРОЕНИЯ

АЛГОРИТМА РЕШЕНИЯ УРАВНЕНИЙ

НАВЬЕ-СТОКСА

Численные методы решения уравнений Навье-

Стокса в процессе своего развития взаимно обо-

гащаются. Поэтом у объединение разных идей и

подходов способствует созданию новых или мо-

дифицированных алгоритмов их расчета. Рассма-

триваемый ниже метод основан на синтезе идей

МАС метода Ф.Х. Харлоу [9, 10], модифициро-

ванного варианта SIMPLE метода С.В. Патанка-

14 Е. В. Бруяцкий, А. Г. Костин, Е. И. Никифорович, Н. В. Розумнюк

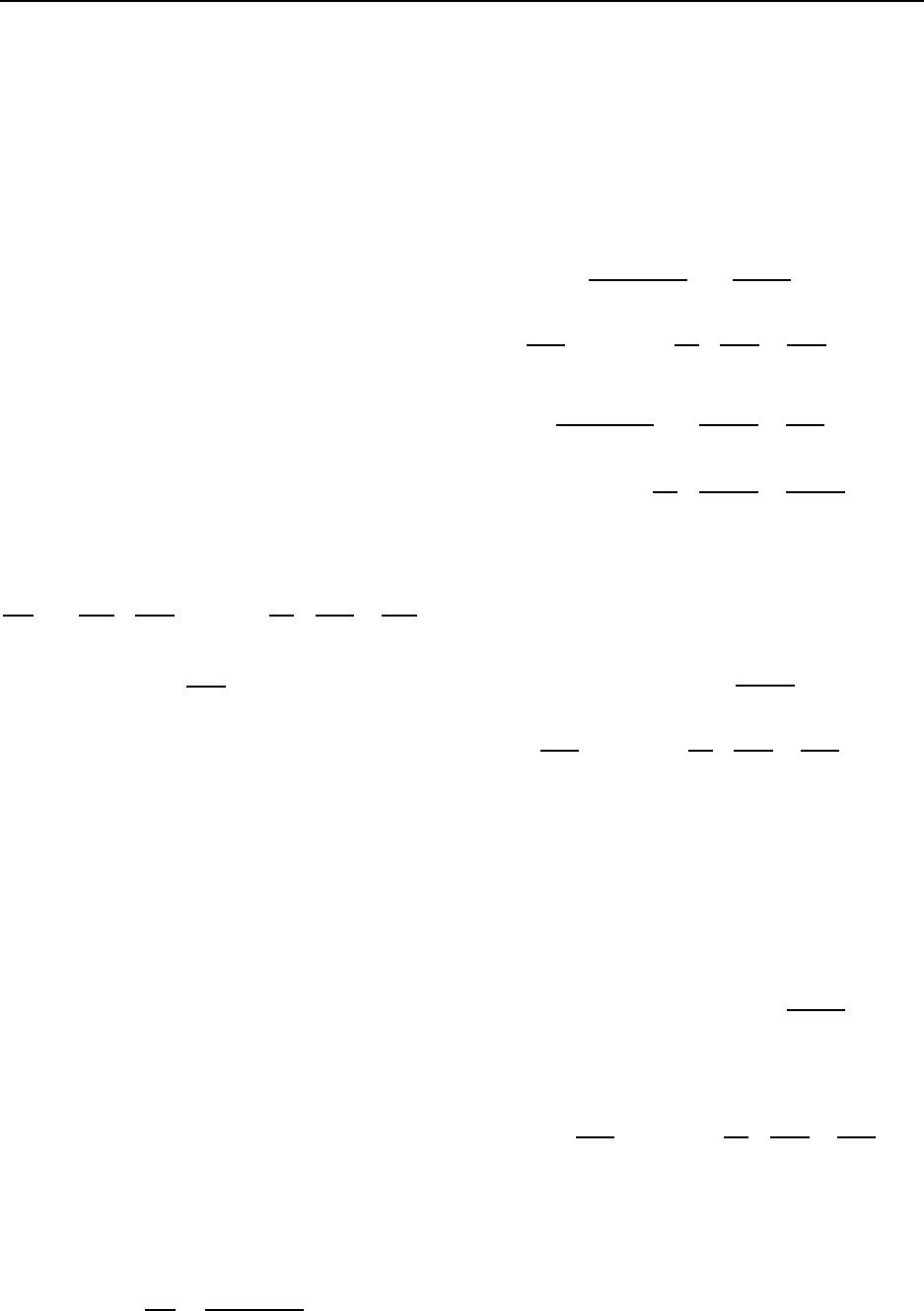
ISSN 1561 -9087 Прикладна гiдромеханiка. 2008. Том 10, N 2. С. 13 – 23

ра и П.В.Сполдинга [17, 18] и метода расщепле-

ния по физическим процессам О.М. Белоцерков-

ского, Ю.М. Давыдова, В.А. Гущина, В.В. Щен-

никова [12, 14, 28, 29].

Ниже развивается единый методологический

подход к решению системы полных нестационар-

ных дифференциальных уравнений Навье-Стокса

в физических переменных скорость–давление для

несжимаемой жидкости. Заметим, что одна из

основных трудностей численного решения этих

уравнений, наряду с нелинейностью, связана с ра-

счетом поля да вления, для которого отсутствует

отдельное уравнение и граничные усло вия. Пре-

длагаемый метод не зависит о т пространственной

размерности задачи.

Рассмотрим исходную систему уравнений

Навье-Стокса в прямоугольной декартовой си-

стеме координат. При отсутствии внешних сил

эта система исходных нестационарных уравнений

движения несжимаемой жидкости может быть

записана в следующей дивергентной тензорной

форме [30, 32]:

∂V

∂τ

= −

∂P

∂X

∂

∂X



−V



∂V

∂X

∂V

∂X



∂V

∂X

= 0. (1)

Уравнения (1) записаны в безразмерных вели-

чинах с ипользованием общепринятых обозначе-

ний: V – скорость, P – давление, τ – время, Re =

l/ν – число Рейнольдса. По повторяющемуся ин-

дексу подразумевается суммирование.

Для решения этой системы уравнений Навье-

Стокса будем использовать метод установления.

Поясним кратко предлагаемую общую схему чи-

сленного решения рассматриваемой системы урав-

нений. Пусть в некоторый момент времени τ

n·∆τ (∆τ – шаг по времени, n – число шагов) изве-

стны значения полей скорости V

и давления P

Требуется определить значения этих параметров

течения в момент времени τ

n+1

при заданных на-

чальных и граничных условиях рассматрива емой

задачи. Если использовать метод конечных разно-

стей, то одной из первых проблем, возникающих

при численном моделировании каких-либо тече-

ний, является задача выбора шаблона расчетной

сетки и метода дискретизации исходных уравне-

ний. Для дискретизации по времени используем

простейшую схему первого порядка точности с по-

мощью односторонних разностей, то есть

∂V

∂τ

n+1

− V

∆τ

Далее введем в пространстве (X

, τ) основную

прямоугольную сетку, состоящую из точек X

i,0

+ h

в соотвествии с декартовой системой ко-

ординат. Множество точек X

(i = 1, 2, 3) о бразу-

ют сетку. Известно, что дискретизацию исходных

уравнений (1) можно выполнить двумя различны-

ми способами – по явной и по неявной схеме соо-

тветственно:

n+1

− V

∆τ

= −

∂P

n+1

∂X

∂

∂X



−V



∂V

∂X

∂V

∂X



, (2)

n+1

− V

∆τ

= −

∂P

n+1

∂X

∂

∂X



−V

n+1



∂V

n+1

∂X

∂V

n+1

∂X



. (3)

Здесь верхний индекс n означает последователь-

ные дискретные моменты времени. Для простоты

и наглядности общего принципа рассмотрим сна-

чала вариант явной схемы и перепишем уравнение

(2) в следующей форме:

n+1

= V

− ∆τ

∂P

n+1

∂X

+∆τ

∂

∂X



−V



∂V

∂X

∂V

∂X



. (4)

Далее, при нашем подходе удобно перейти к

операторной форме рассматриваемого исходного

уравнения. Обозначим все конвективные и диф-

фузионные слагаемые системы уравнений (4) с по-

мощью оператора G

). То гда в символической

форме дискретная по времени с шагом ∆τ явная

схема этих уравнений запишется в виде:

n+1

= V

+ ∆τ



) −

∂P

n+1

∂X



, (5)

где соответствующий оператор G

) имеет вид:

) =

∂

∂X



−V



∂V

∂X

∂V

∂X



(6)

Нетрудно видеть, что для получения замкну-

той системы уравнений необходимо иметь допол-

нительное уравнение для определения давления.

Так как искомая скорость V

n+1

должна удов ле-

творять не т олько уравнениям движения (5), но и

уравнению неразрывности на (n+1) шаге, то есть:

Е. В. Бруяцкий, А. Г. Костин, Е. И. Никифорович, Н. В. Розумнюк 15

ISSN 1561 -9087 Прикладна гiдромеханiка. 2008. Том 10, N 2. С. 13 – 23

Рис. 1. Фрагмент расположения узлов и ячеек на

разнесенной сетке

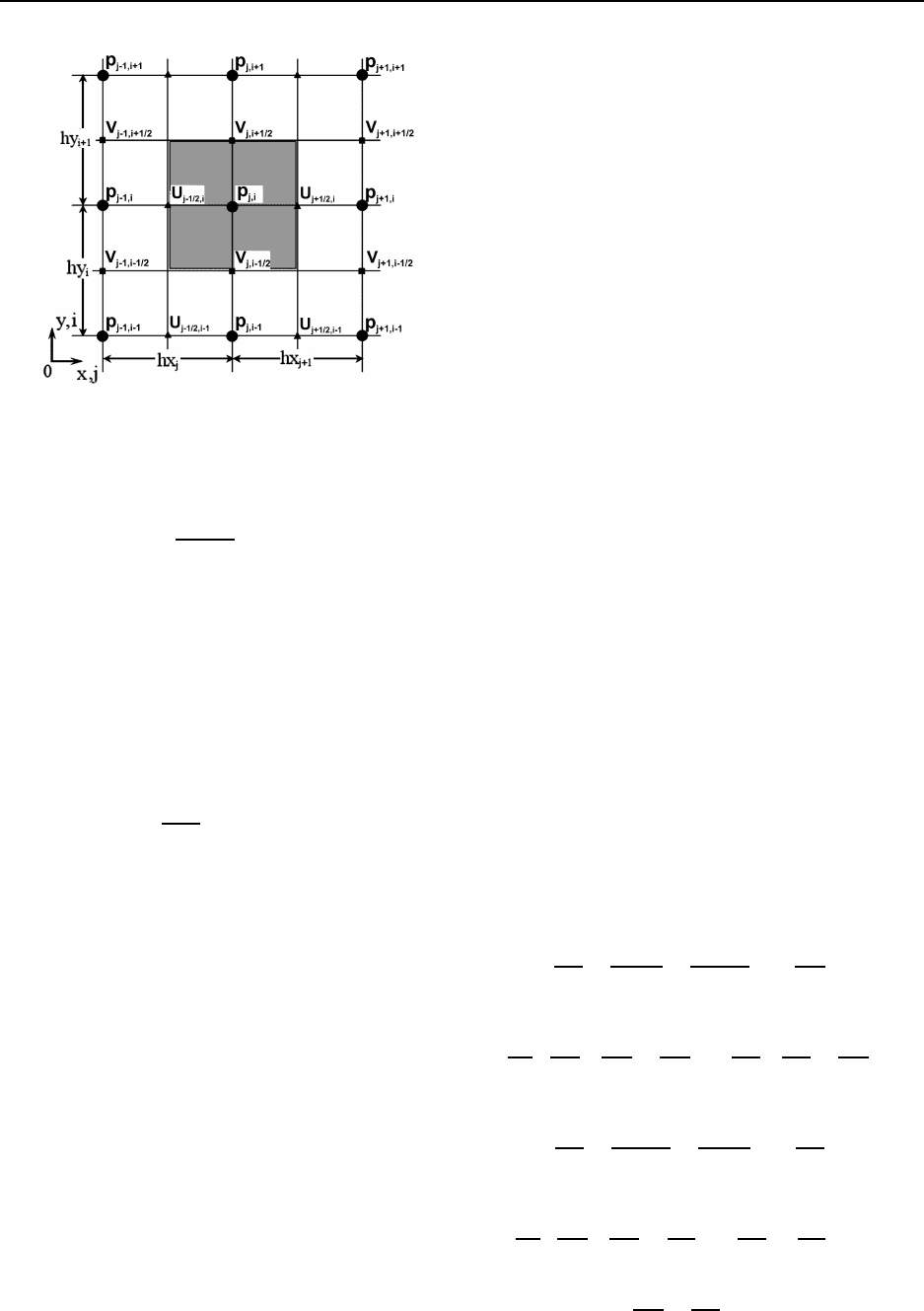
∂V

n+1

∂X

= 0, (7)

то этот факт можно использовать для получе-

ния недостающего уравнения для давления. Дей-

ствительно, следуя алгоритму методов МАС и SI-

MPLE, подставим выражение (5) в уравнение не-

разрывности (7). Тогда, выполнив соответствую-

щие преобразования полученного выражения, на-

ходим уравнение для определения давления на

(n + 1) шаге в виде следующего ра зностного урав-

нения типа Пуассона:

∆P

n+1

∂

∂X



/∆τ + G

)



. (8)

Здесь ∆ – оператор Лапласа, а правая часть урав-

нения (8) определена через величины с предыду-

щего шага. Таким образом, для расчета поля ско-

ростей и давления на (n + 1) временном шаге име-

ем замкнут ую систему уравнений (5), (8), которая

представляет собой эволюционную задачу матема-

тической физики со специфическими оператора-

ми. Из этой системы уравнений следует, что если

в момент времени τ скорость и давление в рассма-

триваемой расчетной области известны, то мож-

но их определить в следующий момент времени

τ + ∆τ .

На данном этапе предположим, что конечно-

разностная аппроксимация соответствующих

дифференциальных операторов по про странс-

твенным переменным на принятом шаблоне

уже осуществлена. Этот прием позволяет со-

средоточить внимание на основных положениях

предлагаемого метода. Этап дискретизации конве-

ктивных и диффузионных слага емых в исходных

уравнениях можно выполнить различными спосо-

бами. Один из них для двумерной задачи будет

рассмотрен ниже. Учитывая сказанное, констру-

ктивный путь рассматриваемого метода расчета

искомых функций V

n+1

и P

n+1

в момент времени

n+1

= (n + 1) · ∆τ на описательном уровне пред-

ставляется в виде следующей вычислительной

процедуры.

На первом этапе по известным с предыдуще-

го шага значениям скоростей V

вычисляются

значения величин G

) с помощью алгебраиче-

ских формул, полученных в процессе дискретиза-

ции выражения (6). На второ м этапе, зная правую

часть уравнения Пуа ссона (8), путем его решения,

рассчитывается поле давления P

n+1

. На третьем

этапе, по найденному полю дав ления P

n+1

и ско-

рости V

согласно ура внению (5) рассчитывается

поле скорости V

n+1

на (n+1) шаге. На этом расчет

текущего временного цикла заканчивается. Далее

эта процедура повторяется до получения сходяще-

гося решения. Отметим, что в данном алгоритме,

скорость, рассчитываемая на каждой новой итера-

ции по времени, уже удовлетворяет уравнению не-

разрывности и нет необходимости строить какие-

либо поправки. Это обстоятельство существенно

отличает данный метод от других [17, 20].

2. ЧИСЛЕННЫЙ МЕТОД

Продолжим рассмотрение предлага емого мето-

да на прим ере двухмерной задачи. Вектор скоро-

сти V

будем задавать двумя проекциями U, V на

X, Y направления со ответственно.

Выпишем систему нестационарных уравнений

Навье-Стокса (1) для двумерного случая в прое-

кциях на оси декартовой прямоугольной системы

координат в виде:

∂U

∂τ

∂(U

)

∂X

∂(U V )

∂Y

= −

∂P

∂X



∂

∂X



∂U

∂X

∂U

∂X



∂

∂Y



∂U

∂Y

∂V

∂X



(9)

∂V

∂τ

∂(U V )

∂X

∂(V

)

∂Y

= −

∂P

∂Y



∂

∂X



∂V

∂X

∂U

∂Y



∂

∂Y



∂V

∂Y



, (10)

∂U

∂X

∂V

∂Y

= 0. (11)

16 Е. В. Бруяцкий, А. Г. Костин, Е. И. Никифорович, Н. В. Розумнюк

ISSN 1561 -9087 Прикладна гiдромеханiка. 2008. Том 10, N 2. С. 13 – 23

В силу сложностей согласования полей скоро-

сти и давления, численный алгоритм конечно-

разностной схемы удобно реализовать на разно-

стной сетке с разнесенной структурой располо-

жения сеточных узлов. Это означает, что зависи-

мые переменные скорость и давление определяю-

тся в разных узлах сетки. Поэтому введем в про-

странстве (X, Y, τ ) основную прямо угольную се-

тку S

, Y

, τ

), состоящую из точек:

= X

+j ·∆x, Y

= Y

+i·∆y, τ

= n·∆τ

и две вспом огательные полуцелые сетки S

и S

j+1/2

, Y

, τ

), X

j+1/2

= X

+(j + 1/2) · ∆x,

= i · ∆y, τ

= n · ∆ τ ;

, Y

i+1/2

, τ

), X

= j · ∆x,

i+1/2

= Y

+ (i + 1/2) · ∆y, τ

= n · ∆τ.

Выбрав такой сеточный шаблон, вв едем следу-

ющие обозначения:

P (X

, Y

, τ

) = P

j,i

;

U((j + 1 /2) · ∆x, i · ∆y , n · ∆τ ) = U

j+1/2,i

;

V (j · ∆x, (i + 1/2) · ∆y, n · ∆τ ) = V

j,i+1/2

Конечно-разностные аналоги уравнений (9)–

(11) будем строить на пятиточечном шаблоне в

соответствии с известной схемой "крест" [31]. Рас-

сматриваемая область течения разбивается орто-

гональной сеткой на контрольные о бъемы (ячей-

ки), в центрах которых находятся узлы основной

сетки S

(j, i). Схема ра сположения ячеек и узлов

аналогична схеме метода МАС [4, 9, 12, 16] и при-

ведена на рис. 1.

В узлах основной сетки расположены сеточные

функции давления P

j,i

. Сеточные функции ком-

понентов скорости находятся на серединах граней

контрольных объемов, то есть в узлах вспомога-

тельных полуцелых сеток S

(j + 1/2, i) и S

(j, i +

1/2) соот ветственно. Шаги сеток могут быть как

равномерными, так и переменными в обоих на-

правлениях.

Внешние границы расчетной области выбираю-

тся с учетом совпадения граней в ну тренних при-

граничных ячеек с физическими границами обла-

сти, где задаются граничные условия для ком-

понентов скорости. При таком подходе сеточные

функции давления находятся внутри расчетной

области и не попадают на физическую границу

Рис. 2. Принципиальная схема течения в плоском

прямолинейном канале

, что по зво ляет согласовать поля скорости и

давления.

Граница расчетной сетки D

состоит из ячеек

с центрам и в узлах (1, i), (N, i), (j, 1), (j, M ), где N

и M – число ячеек сетки в направлениях X и Y

соответственно, а точка (j, i) совпадает с центром

ячейки [9 – 11]. В схему включены также слои фи-

ктивных ячеек (0, i), (N + 1, i), (j, 0), (j, M + 1).

При дискретизации рассматриваемых уравне-

ний, как уже отмечалось выше, производные по

времени аппроксимируются по обычной схеме пер-

вого порядка точности, например,



∂U

∂τ



j+1/2,i

n+1

j+1/2,i

− U

j+1/2,i

∆τ

, (12)

а конечно-разностные аналоги по пространствен-

ным переменным для соответствующих произво-

дных, входящих в исходную систему уравнений,

центрируются в соответствии с выбранным шабло-

ном. Например, слага емые с градиентом давления

вычисляются с помощью односторонних разностей

по формулам вида:



∂P

∂X



n+1

j+1/2,i

n+1

j+1,i

− P

n+1

j,i

j+1

. (13)

Для аппроксимации диффузионных членов

уравнений используется схема с центральными ра-

зностями, как например:



∂

∂X



j+1/2,i

j+3/2,i

− 2U

j+1/2,i

+ U

j−1/2,i

∆x

(14)



∂

∂Y



j+1/2,i

j+1/2,i+1

− 2U

j+1/2,i

+ U

j+1/2,i−1

∆y

(15)

Конвективные слагаемые исходных уравнений

аппроксимируются по следующим формулам:

Е. В. Бруяцкий, А. Г. Костин, Е. И. Никифорович, Н. В. Розумнюк 17

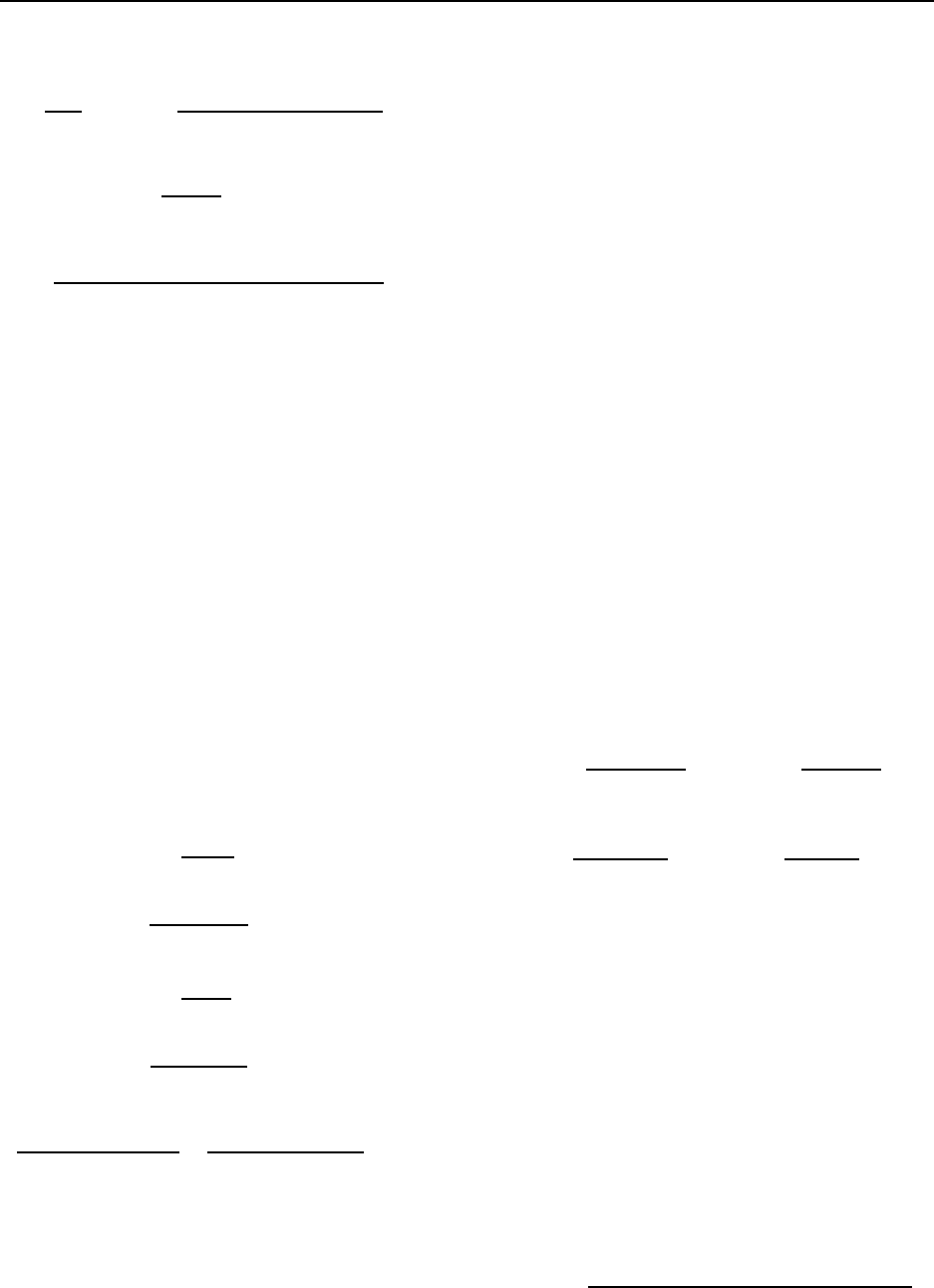
ISSN 1561 -9087 Прикладна гiдромеханiка. 2008. Том 10, N 2. С. 13 – 23



∂U

∂X



j+1/2,i

(U · U)

j+1,i

− (U · U)

j,i

j+1

, (16)



∂(U V )

∂Y



j+1/2,i

(U · V )

j+1/2,i+1/2

− (U · V )

j+1/2,i−1/2

∆y

, (17)

а для уменьшения влияния численной вязкости

на устойчивость решения используется разностная

схема “против потока” [4, 24]. Более полные выра-

жения конечно-разностных аналогов соответству-

ющих слагаемых двухмерных и трехмерных урав-

нений движения приведены, например, у О.М. Бе-

лоцерко вского [12] и К.Флетчера [16]. Использу-

емая конечно-разностная схема аппроксимирует

рассматриваемые уравнения с первым порядком

точности по времени и со вторым порядком точно-

сти по про странственным переменным O(∆τ, h

)

и можно показать, что она устойчива. Подста-

вим конечно-разностные формулы в исходную сис-

тему уравнений движения (9)–(11). Тогда после

простых преобразований получим их дискретные

аналоги для и Y направлений соответственно.

Полученные разностные а лгебраические уравне-

ния, разрешенные относительно компонентов ско-

ростей U

n+1

j+1/2,i

, V

n+1

j,i+1/2

, и дополненные уравнени-

ем неразрывности, преобразуются к следующему

конечно-разностному виду:

n+1

j+1/2,i

= −

∆τ

j+1

n+1

j+1,i

− P

n+1

j,i

2∆τ

hy1 · hx

j+1

j+1/2,i

, (18)

n+1

j,i+1/2

= −

∆τ

i+1

n+1

j,i+1

− P

n+1

j,i

2∆τ

hx1 · hy

i+1

j,i+1/2

, (19)

n+1

j+1/2,i

− U

n+1

j−1/2,i

∆x

n+1

j,i+1/2

− V

n+1

j,i−1/2

∆y

= 0. (20)

Здесь алгебраические выражения G

j+1/2,i

j,i+1/2

, полученные в результате дискретизации,

являются известными величинами. Соответствую-

щие форм улы для них здесь не приводятся вви-

ду их сложности и ограниченности объема ста-

тьи. Шаги сетки приняты переменными и для

них использованы следующие обозначения: ∆x =

0.5(hx

+ hx

j+1

), ∆y = 0.5(hy

+ hy

i+1

), hx

(hx

+ hx

j+1

), hy

= (hy

+ hy

i+1

Полученная система конечно-разностных урав-

нений хотя и является основной, но пока содер-

жит неизвестные слагаемые с градиентом давле-

ния. Поэтому для ее дальнейшего решения исполь-

зуется модифицированный алгоритм SIMPLE [17].

В соответствии с ним давление будем опреде-

лять, используя уравнение неразрывности (20).

Учитывая его структуру, понизим предваритель-

но в выражениях для скоростей U

n+1

j+1/2,i

и V

n+1

j,i+1/2

индексы j и i на единицу соответственно. Тогда

получим необходимые выражения для U

n+1

j−1/2,i

n+1

j,i−1/2

. Подставим соответствующие выражения

для компонентов скоростей в уравнение (20). То-

гда после простых преобразований получим сле-

дующее разностное уравнение Пуассона для дав-

ления:

j,i

n+1

j,i

+ c

n+1

j+1,i

+ c

j−1,i

+ b

n+1

j,i+1

n+1

j,i−1

= f

(j, i). (21)

Здесь значение свободного члена f

(j, i) изве-

стно по данным с предыдущего шага, а соответ-

ствующие коэффициенты дискретизации уравне-

ния (21 ) определяются по формулам:

= −

hx1 · hx

j+1

, c

= −

hx1 · hx

= −

hy1 · hy

i+1

, b

= −

hy1 · hy

, (22)

j,i

= −c

− c

− b

Для повышения устойчивости разностной схемы

данный подход обобщен на случай неявной разно-

стной схемы. При этом идейная сторона метода

полностью сохраняется, но выра жения для основ-

ных постоянных величин несколько видоизменя-

ются. Однако ключевое уравнение для давления

сохраняет свой вид (21) с заменой постоянных ве-

личин, например, f

(j, i) на

(j, i) и так далее.

А система уравнений для компонентов скорости

приобретает вид:

n+1

j+1/2,i

0.5 · hy1(P

n+1

j,i

− P

n+1

j+1,i

) +

j+1/2,i

(23)

18 Е. В. Бруяцкий, А. Г. Костин, Е. И. Никифорович, Н. В. Розумнюк

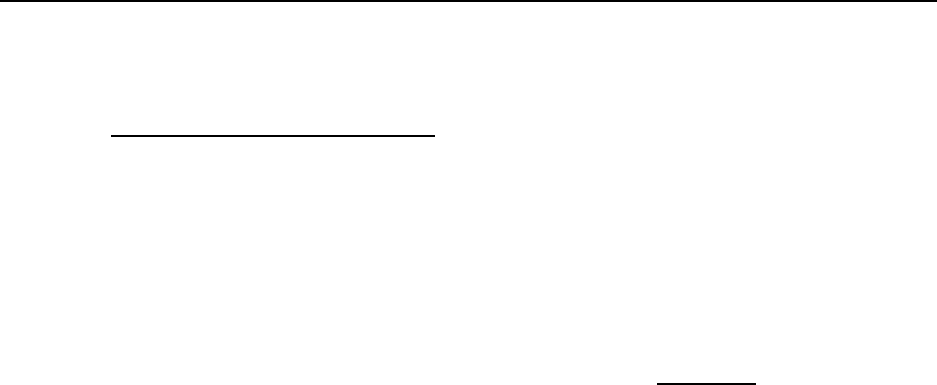
ISSN 1561 -9087 Прикладна гiдромеханiка. 2008. Том 10, N 2. С. 13 – 23

n+1

j,i+1/2

0.5 · hx1(P

n+1

j,i

− P

n+1

j,i+1

) +

j,i+1/2

(24)

где выражения

j+1/2,i

j,i+1/2

несколько ви-

доизменяются по сравнению с явной схемой и

появляются новые алгебраические коэффициенты

j+1/2,i

и d

j,i+1/2

, зависящие от значений искомых

переменных с предыдущего шага.

Полученная система конечно-разностных урав-

нений (18), (20), (21) или (21), (23), (24), моде-

лирующих движение несжимаемой жидкости, но-

сит фундаментальный характер и является уни-

версальным дискретным аналогом полных урав-

нений Навье-Стокса. Она представляет собой сис-

тему алгебраических уравнений, связывающих яв-

но искомое давление с компонентами скорости,

на (n + 1) временном шаге, которые удовлетворя-

ют уравнению неразрывности. Решение получен-

ной системы разностных алгебраических уравне-

ний такого вида осуществляется известными ите-

рационными методами. Важной особенностью по-

лученного разностного уравнения Пуассона (21)

является то, что благодаря использованию разне-

сенных сеток, граничные условия для его реше-

ния не требуются, так как они могут быть опре-

делены с помощью комбинации уравнений движе-

ния и граничных условий для компонентов ско-

рости [16] . При это м полученный универсальный

дискретный аналог уравнений движения позволя-

ет определить граничные значения давления сра-

зу в явном виде. Эффективным способом решения

двумерного разностного уравнения второго поряд-

ка является алгоритм используемый в методе "пе-

ременных направлений", который состоит в ре-

дукции исходного уравнения для дав ления (21) к

двум одномерным уравнениям второго порядка с

трехдиагональными матрицами, которые решаю-

тся методом прогонки.

В данном методе расчеты проводятся для двух

основных физических переменных – скорости и

давления. Итерационный вычислительный про-

цесс состоит из шагов по времени. В начале каждо-

го временного цикла предполагаются известными

поля скорости и давления. Вычислительная про-

цедура выполняется в следующей последователь-

ности. По известным на предыдущем временном

шаге значениям U

j+1/2,i

и V

j,i+1/2

по соотв етству-

ющим алгебраическим формулам рассчитываются

коэффициенты дискретизации G

j+1/2,i

, V

) и

j+1/2,i

, V

), включая свободный член f

(j, i).

Определив таким образом прав ую часть уравне-

ния Пуассона, путем его решения находится по-

ле давления P

n+1

. Далее зная коэффициенты дис-

кретизации и поле давления P

n+1

по уравнениям

(18), (19), или (23), (24), рассчитываются поля ско-

рости U

n+1

j+1/2,i

, V

n+1

j,i+1/2

на (n+1) шаге. На этом пер-

вый расчетный цикл заканчивается и далее он по-

вторяется. Задача решается на установление. Кри-

терием окончания решения служит условие, когда

максимальная относительная разность между зна-

чениями искомых переменных на предыдущем и

следующем временном шаге не превышает задан-

ную величину ошибки ε, то есть:

max



n+1

− U

n+1



≤ ε. (25)

Важным моментом расчетов является контроль

за выполнением уравнения неразрывности.

3. ПОСТАНОВКА ЗАДАЧИ О ТЕЧЕНИИ

НА НАЧАЛЬНОМ УЧАСТКЕ

В ПЛОСКОМ КАНАЛЕ

Для проверки новых или модифицированных

численных схем и концепций важно выбрать под-

ходящую модельную задачу. В данной работе для

тестирования предлагаемой численной схемы вы-

брана задача о расчете начального участка в пло-

ском прямолинейном канале. Интерес к этой за-

даче обусловлен тем, что она имеет простейшую

геометрию и в то же время содержит всю сло-

жность и особенности решения полных уравне-

ний Навье-Стокса [ 3, 21]. Кроме того, на устано-

вившемся участке канала рассматриваемое тече-

ние имеет точное аналитическое решение в ви-

де известного параболического профиля Пуазей-

ля, что позволяет надежно оценить качество чи-

сленной схемы и т очность метода.

Рассмотрим ламинарное течение несжимаемой

вязкой жидкости в плоском прямолинейном кана-

ле. Принципиальная схема в ы нужденного т ечения

в канале и конфигурация расчетной области АВ-

СD, на которой заданы граничные условия для

компонентов скорости, представлены на рис. 2.

Начало введенной декартовой системы координат

находится в левом нижнем углу прямоугольной

области АВСD.

Для описания движения жидкости использую-

тся нестационарные двумерные уравнения Навье-

Стокса без каких-либо упрощающих предположе-

ний. Для введения безразмерных величин за мас-

штаб длины принимается ширина канала h, за

масштаб скорости принята среднерасходная ско-

рость в канале u

= Q/ h, за масштаб време-

ни принята величина h /u

, а за масштаб давле-

Е. В. Бруяцкий, А. Г. Костин, Е. И. Никифорович, Н. В. Розумнюк 19

ISSN 1561 -9087 Прикладна гiдромеханiка. 2008. Том 10, N 2. С. 13 – 23

0,0

0,2

0,4

0,6

0,8

1,0

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5

x=0.93

x=1.24

x=2.17

x=3.1

x=4.65



U

y

0,0

0,2

0,4

0,6

0,8

1,0

-0,04 -0,02 0,00 0,02 0,04

x=0.93

x=1.24

x=1.55

x=2.17

x=4.65



V

y

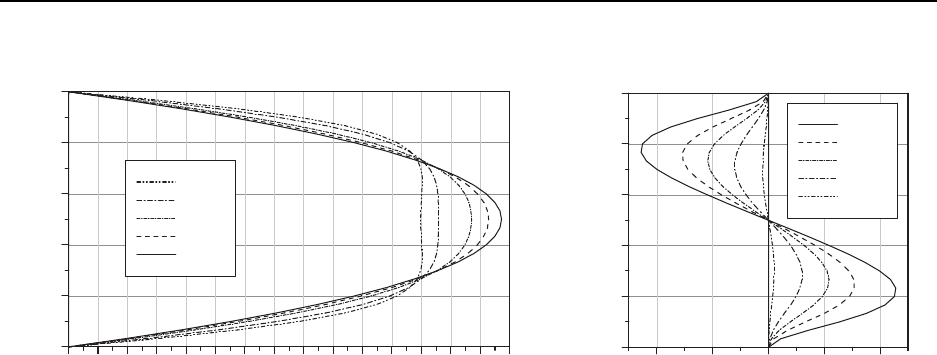
Рис. 3. Расчетное распределение горизонтальной (U ) и вертикальной скоростей (V ) на начальном участке

плоского канала в различных поперечных сечениях (Re=100)

ния принят скоростной напор ρ

. В безразмер-

ных величинах U = u/u

, V = v/u

, X = x/h,

Y = y/h, τ = tu

/h, P = p/ρ

система неста-

ционарных двумерных уравнений Навье-Стокса с

постоянными плотностью и кинематической вяз-

костью в консервативной форме записана выше в

виде системы уравнений (9)–(11).

Характерной особенностью течений в каналах

является то, что движение жидкости происходит

под действием продольного перепада давления,

который на установившемся участке течения по-

стоянен ∂P/∂X = const. Однако заданной величи-

ной в рассматриваемом классе течений примем не

перепад давления, а расход жидкости Q = u

· h

через поперечное сечение канала. Следовательно,

при такой постановке задачи число Рейнольдса

будет задано, а давление должно определяться в

процессе решения. Для завершения постановки за-

дачи должны быт ь заданы начальные и грани-

чные условия на всех границах расчетной области.

Учитывая, что U и V являются компонентами

скорости вдоль X и Y направлений соответствен-

но и жидкость втекает в исследуемую область сле-

ва направо, то на верхней ВС и нижней АD не-

подвижных твердых стенках граничные условия

для скорости задаются в виде условий прилипа-

ния U |

= 0 и не протекания V |

= 0 . На вхо-

де в расчетную обла сть используется условие не-

возмущенного потока U |

= 1 , V |

= 0 . При

постановке граничного условия в сечении СD, на

выходе из расчетной об ласти, мы сталкиваемся

с проблемой моделирования граничного условия

на бесконечности. В данном случае простейший

способ постановки граничного условия на "выхо-

де"состоит в использовании так называемых "м яг-

ких"условий. Таким образом, начальные и грани-

чные условия рассматриваемой задачи имеют вид:

начальные условия: U = 1; V = 0; P = 0,

граничные условия:

U |

= 1 ; U |

= 0 ; U |

= 0 ; ∂U/∂X |

= 0;

V |

= 0 ; V |

= 0 ; ∂V/∂X |

= 0 .

(26)

Кроме того, на выходе из расчетной области

распределение горизонтальной скорости U в вер-

тикальном направлении соответствует известному

профилю Пуазейля U (Y ) = 6(1 − Y )Y .

Граничные условия для давления в постановке

задачи отсутствуют. Но при нашем подходе необ-

ходимые значения давления в граничных узлах

определяются с помощью уравнений движения в

комбинации с граничными условиями для скоро -

стей. По существу они представляют собой усло-

вия Неймана

∂P/∂n |

= µ

где n – нормаль к границе области Γ, а µ

– из-

вестная величина.

В процессе решения задачи необходимо опреде-

лить эволюцию полей скорости, да вления и дли-

ну начального участка стабилизации течения при

различных числах Рейнольдса. Так как исходная

система уравнений (9)–(11) содержит три уравне-

ния и три неизвестных, а именно, две ко мпоненты

скорости и давление, то задача замкнута.

20 Е. В. Бруяцкий, А. Г. Костин, Е. И. Никифорович, Н. В. Розумнюк

ISSN 1561 -9087 Прикладна гiдромеханiка. 2008. Том 10, N 2. С. 13 – 23

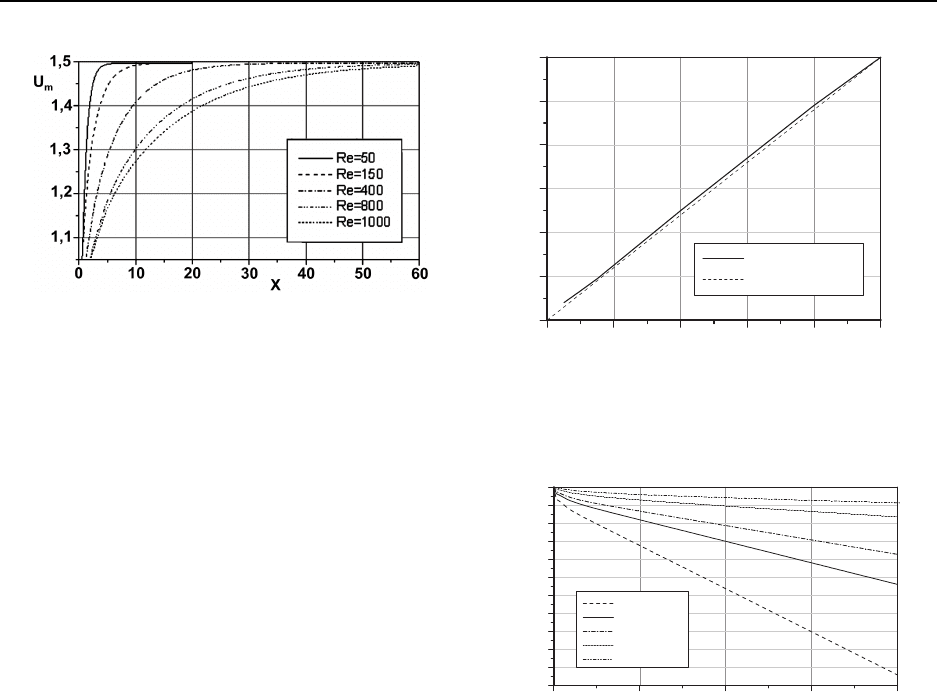
Рис. 4. Расчетные зависимости безразмерной осевой

скорости U

от расстояния X на участке

стабилизации течения при различных числах

Рейнольдса

Описанная выше численная схема решения

уравнений Навье-Стокса в виде универсального

дискретного анало га (21)–(24) была реализована

в виде компьютерной программы.

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ

И ИХ ОБСУЖДЕНИЕ

Некоторые характерные результат ы расчетов

распределения полей продольной и поперечной

скоростей, длины начального участка и поля дав-

ления представлены ниже на соответствующих ри-

сунках. Как и следовало ожидать, расчеты по-

казали, что в ближней от входа в канал обла-

сти профиль скорости зависит от координаты X.

Этот участок канала принято называт ь участком

гидродинамической стабилизации. Критерием его

протяженности может служить условие [21]

(1 − U

) ≤ ε, (27)

где U

– локальная осевая скорость в канале;

= 6(1 − Y )Y |

y=0.5

= 1.5 – осевая скорость

установившегося течения, соответствующая про-

филю Пуазейля. На рис. 3 представлены резуль-

таты расчетов профилей горизонтальной и верти-

кальной скорости в различных сечениях канала на

участке гидродинамической стабилизации. Приве-

денные на рисунке расчетные профили соответ-

ствуют различным расстояниям поперечных сече-

ний от входа в канал. Координату X для каждо-

го профиля можно получить, умножив его номер

на соответствующий шаг h = L/N , где L – дли-

на расчетной обла сти, а N – число расчетных то-

чек. Анализ этих результатов показывает, что не-

посредственно вблизи от входа в канал (X = 0.93 и

X = 1.24) в поле течения существует ядро с посто-

200 400

600

800

1000

Õ 0.06*Re

Ðàñ÷åò

Рис. 5. Расчетная зависимость длины начального

участка X

от числа Рейнольдса

-10

-8

-6

-4

-2

Re=50

Re=100

Re=150

Re=400

Re=1000

Рис. 6. Расчетное распределение давления вдоль оси

X при различных значениях числа Рейнольдса

янным значением горизонтальой скорости, а вбли-

зи стенок развиваются пограничные слои. С уда-

лением от входного сечения профиль горизонталь-

ной скорости U постепенно эволюционирует в па-

раболу, которая реализуется в конце участка ста-

билизации в результат е соединения пограничных

слоев. В данном методе расчитывается и верти-

кальная скорость течения V , которая, ка к видно

из рис. 3, имеет место вблизи входного сечения в

канал, а затем быстро стремится к нулю.

Расчетные профили горизонтальных и верти-

кальных скоростей сравнивались с аналогичными

расчетами, полученными другим методом [21], ко-

гда исходные уравнения записываются в перемен-

ных функция тока – вихрь. Для приведенных

там результатов расчета наблюдается хорошее со-

ответствие с нашими результатами. Отметим, что

наш метод позволяет охватить диапазон измене-

ния чисел Рейнольдса от 1 до 1000. Выполненные

численные расчеты безразмерной осевой скорости

в центральной плоскости канала в зависимости

Е. В. Бруяцкий, А. Г. Костин, Е. И. Никифорович, Н. В. Розумнюк 21

ISSN 1561 -9087 Прикладна гiдромеханiка. 2008. Том 10, N 2. С. 13 – 23

от расстояния X при различных числах Рейнольд-

са приведены на рис. 4. Они наглядно иллюстри-

руют асимптотический характер приближения ра-

счетных профилей к параб оле Пуазейля.

На рис. 5 представлена расчетная длина на-

чального участка X

при различных числах Рей-

нольдса, которая определялась из условия (27)

при ε ≤ 1%. Легко видеть, что в инт ервале чисел

Рейнольдса от 100 до 1000 эта расчетная зависи-

мость, обозначенная на рисунке сплошной лини-

ей, хорошо аппроксимируется линейной функцией

(Re) = 0.06Re.

Полученное нами расчетное значение длины на-

чального участка X

при Re=1000 равно 60. Зна-

чение, приведенное у Г. Шлихтинга [3], получен-

ное с использованием зависимостей теории погра-

ничного слоя для числа Re=2000, равно 80. По-

скольку исходные уравнения движения записаны

и решаются в переменных скорость–давление, то

это позволяет в процессе решения сразу рассчи-

тывать и поле давления в канале. В качестве при-

мера на рис. 6 представлено расчетное распреде-

ление давления в доль центральной плоскости ка-

нала в зависимости от числа Рейнольдса. Расче-

ты показывают, что давление монотонно убыва-

ет вдоль канала, приближаясь к перепаду дав-

ления, соответствующему течению на установив-

шемся участке. Расчетное давление в поперечном

направлении Y , как и следовало ожидать, в ка-

ждом сечении X постоянно, за исключением не-

посредственной близости о т входа в канал, где на-

блюдается перестройка как давления, так и скоро-

сти.

ВЫВОДЫ

Развит эффективный метод численного реше-

ния полной системы нестационарных уравнений

Навье-Стокса в переменных скорость-дав ление в

случае несжимаемой жидкости. Пут ем конечно-

разностной аппроксимации получен универсаль-

ный дискретный аналог исходных уравнений дви-

жения ж идкости. В качестве примера методом

установления решена задача о течении жидко-

сти на начальном участке стабилизации течения в

плоском прямолинейном канале. Расчеты показа-

ли, что процесс установления на начальном участ-

ке носит асимпотический характер. С ростом чис-

ла Рейнольдса длина участка стабилизации уве-

личивается, а профиль продольной скорости эво-

люционирует в пара болу Пуазейля. Достоверность

и точность расчетов оценивалась путем контроля

выполнения уравнения неразрывности и анализа

критерия (27), а также сопоставлением наших ра-

счетов с данными эксперимента и результатами

расчетов, полученных другими методами. Исполь-

зуемая численная схема позволяет получить ре-

шение задачи до чисел Рейнольдса Re ≤1000. В

дальнейшем представляется целесообразным про -

должить методические исследования по расчету

данным м етодом более сложных задач, в которых

имеют место возвратные рециркуляционные и ви-

хревые течения.

1. Ламб Г. Гидродинамика.– М.: ГИТЛ, 1947.– 928 с.

2. Лойцянский Л. Г. Механика жидкости и газа.– М.:

Наука, 1978.– 736 с.

3. Шлихтинг Г. Теория пограничного слоя.– М.: Нау-

ка, 1969.– 742 с.

4. Роуч П. Вычислительная гидродинамика.– М.:

Мир, 1980.– 616 с.

5. Chorin A. J. Numerucal solution of the Navier-Stokes

equations // Math.Comput.– 1968.– 22.– P. 745–762.

6. Chorin A. J. A numerical method for solving

incompressible viscous ﬂow problems // J. Comput.

Phys.– 1967.– 2, N1.– P. 12–26.

7. Douglas J., Gunn J. E. A general formulation of

alternating direction implicit methods. Pt. 1. Parabolic

and hyperbolic problems // Numer. Math.– 1964.– 6,

N5.– P. 428–453.

8. Peaceman D. W., Rachford H. H. The numerical soluti-

on of paraboli c and elliptiс diﬀerentional equations //

J. Soc. Indust. Appl. Math.– 1955.– 3, N1.– P. 28–41.

9. Харлоу Ф. Х. Численный метод частиц в ячейках

для задач гидродинамики // Вычислительные ме-

тоды в гидродинамике.–М.: Мир.–1967.– C. 316-342.

10. Harlow F. H. Welch J. E. Numerical calculation of

time-dependent viscouse incompressible ﬂow of ﬂuid

with free surface // Phys. Fluids.– 1965.– 8, N12.–

P. 2182–2189.

11. Пейре Р., Тейлор Т. Д. Вычислительные методы в

задачах механики жидкости.– Л.: Гидрометеоиздат,

1986.– 352 с.

12. Белоцерковский О. М. Численное моделирование в

механике сплошных сред: 2-е изд., перераб. и доп.–

М.: Физматлит, 1994.– 448 с.

13. Марчук Г. И. Методы расщепления.– М.: Наука,

1988.– 264 с.

14. Белоцерковский О. М., Давыдов Ю. М. Нестаци-

онарный метод "крупных частиц"для газодинами-

ческих расчетов // Ж. Вычисл. Матем. И матем.

Физ..– 1971.– 11, N1.– P. 182–207.

15. Рихтмайер Р., Мортон К. Разностные методы ре-

шения краевых задач.– М.: Мир, 1972.– 418 с.

16. Флетчер К. Вычислительные методы в динамике

жидкостей.– М.: Мир, 1991.– T1.-418 с.

17. Патанкар С. Численные методы решения задач

теплообмена и динамики жидкости.– М.: Энерго-

атомиздат, 1984.– 152 с.

18. Patancar S. V., Spolding P. V. C alculation Procedure

for Heat, Mass, and Momentum Transfer in Three-

dimensional Parabolic Flows // Int.j.Heat and Mass

Transfer.– 1972.– 15.– P. 1787–1806.

19. Андерсон Д., Таннехил Дж., Плетчер Р. Вычи-

слительная гидромеханика и теплообмен.– М.: Мир,

1990.– Т.1 - 384 с.

22 Е. В. Бруяцкий, А. Г. Костин, Е. И. Никифорович, Н. В. Розумнюк