Brinkmann R. The Art and Science of Digital Compositing

Подождите немного. Документ загружается.

52 The Art and Science of Digital Compositing

(a) (b)

Figure 3.16 (a) Image with noticeable noise spikes. (b) Same image after application of a median

filter.

As you can see, the bulk of the noise has been eliminated. Applying the filter

again in a second pass would probably eliminate the rest of the noise. This process

does not come without a price, however, since each time a median filter is applied

the image will be slightly softened. For this reason, median filtering is usually

applied only within a certain threshold. The only pixels that will be replaced with

the median of their neighbors are those pixels that vary by more than a certain

amount from the original image. Areas that do not have any noise are not changed,

and the overall image suffers far less softening than a normal median would

produce.

GEOMETRIC TRANSFORMATIONS

The next class of operations we will be discussing all fall under the category of

geometric transformations, or simply ‘‘transforms.’’ A transform operation causes

some or all of the pixels in a given image to change their existing location.

Such effects include panning, rotating, scaling, warping, and various specialized

distortion effects. We’ll first consider the three simplest transformation effects:

pan, rotate, and scale.

Whenever we talk about moving images around, we must realize that they

have to be moved relative to something. It’s easiest to just consider that the image

is being moved relative to some predefined frame. In most day-to-day compositing

work, the first thing we tend to do is define our working resolution, and everything

is moved around inside of this frame. What we call a working resolution is

typically the resolution of the image that will be produced once we are finished

with our compositing operations.

Basic Image Manipulation 53

For the purposes of the next few examples, let’s assume our working resolution

is 1200 pixels wide by 900 pixels tall. Let’s also assume that the input or source

image that we’ll be dealing with in these examples is a slightly smaller resolution,

say 900 ⳯ 600. There is at least one more item we need to know about the system

we are working in, namely, what is considered the origin of our system. In other

words, what part of the frame is considered to have the (X,Y) location of (0,0).

This point may vary between different software packages, but the most common

assumption is that the origin is located in the bottom left corner of the frame.

Thus, our example image when placed (without any additional transformations)

into our working resolution frame is shown in Figure 3.17.

Panning

Let’s say we wish to apply a simple translation to the image, offsetting it in both

X and Y. Such a translation is usually referred to as a pan.

In this case, we will

Figure 3.17 Image in a working resolution frame.

As usual, different software and artists may refer to these operations using different terminology.

Some people would call this a simple reposition, or ‘‘repo.’’ The term ‘‘pan’’ would then be reserved

for a reposition that animates over time. Rather than have a term that is dependent on whether the

54 The Art and Science of Digital Compositing

pan the image by 150 pixels along both axes. The new image produced is shown

in Figure 3.18, with the original image more or less centered within the frame of

our new output image.

What happens if we move the input image 700 pixels in X instead, causing

part of the input image to be moved beyond the borders of our working resolution?

The result will usually be something like what is shown in Figure 3.19a. However,

the issue of what is done with the rest of the image that has moved out of frame

is dependent on the compositing system that is being used. On most systems, the

rest of the image will be cropped, or discarded. Any additional transformations

to this image will be performed with the truncated image, and any portion of the

image that was moved out of the working area will be unrecoverable. A few

systems are able to deal with this problem in a more robust fashion, allowing the

off-screen information to be preserved so that it can later be brought back into

frame if needed. There is also a common option in most systems that lets the user

Figure 3.18 Image from Figure 3.17 panned by 150 pixels along both axes.

effect is applied over time, we have decided to refer to either a static or a dynamic reposition as a

‘‘pan.’’

Basic Image Manipulation 55

(a) (b)

Figure 3.19 Panning. (a) Image panned off-screen. (b) Image panned with wrapping.

specify that the image ‘‘wraps’’ around to the other side of the frame, as shown

of this is shown in Figure 3.19b.

Rotation

Let’s rotate an image now. The two parameters needed to control a simple rotation

are the amount of the rotation (usually specified in degrees) and the center of the

rotation. Changing the center of rotation can dramatically affect the result. Com-

pare Figure 3.20a and Figure 3.20b. Both images have been rotated 30⬚ clockwise,

but in the first the center of rotation was the origin, (0,0), whereas in the second

the image was rotated about a point that is approximately its center.

(a) (b)

Figure 3.20 Rotation. (a) Image rotated 30⬚ clockwise about the origin. (b) Image rotated 30⬚

clockwise about its approximate center.

56 The Art and Science of Digital Compositing

Scale

Now we will look at the case of scaling an image. Again, if your compositing

system supports it, the ability to scale around a user-defined point is useful.

Figures 3.21a and 3.21b show an image scaled down by 50% (or scaled by 0.5)

around the same two origins that we used for our rotation examples. If for some

reason your compositing system does not support scaling around a user-defined

origin, don’t be too concerned, since it is really just a shortcut that can easily be

duplicated by panning the resulting image into the position we desire.

Although this example shows an image scaled by the same amount (0.5) in

both X and Y, we can certainly scale nonuniformly instead, say by 0.3 in X and

by 1.2 in Y. Note that we can also ‘‘flip’’ or ‘‘flop’’ an image by scaling it by ⳮ1

in the X or Y direction, respectively. Remember that flipping an image is not the

same as merely turning it upside-down (i.e., rotating it by 180⬚). Instead, flipping

produces a mirror image along the X axis. This can be very useful when faking

shadows or reflections in a composite. Figure 3.22 illustrates the difference between

an image that is flipped (3.22a) and one that is merely rotated (3.22b).

3D Transforms

So far we’ve confined our discussion of various transformations to what are

considered to be 2D transforms. We can also choose to rotate an image as if it

were being moved about within a 3D environment. Various perspective

effects

(a) (b)

Figure 3.21 Scaling. (a) Image scaled by 50% around the origin. (b) Image scaled by 50% around

its approximate center.

Perspective is discussed in greater detail in Chapter 12.

Basic Image Manipulation 57

(a) (b)

Figure 3.22 (a) Flipped image. (b) Rotated image.

will consequently be introduced. Without going into great detail to define the

information needed to extend our discussion into this third dimension, let’s just

look at a simple example of transforming an image in 3D space. Figure 3.23 shows

an image that has been partially rotated around the X-axis. You can see the obvious

Figure 3.23 Three-dimensional rotation around the X-Axis.

58 The Art and Science of Digital Compositing

perspective effects, whereby foreshortening causes the bottom of the image to be

compressed and the top of the image to be enlarged.

Even if your compositing system doesn’t support the concept of perspective

transformations, it may support something known as ‘‘corner-pinning,’’ in which

the user can manually reposition the four corners of an image to create any

arbitrary tetrahedron. The end visual result should be similar.

In general, most

3D transformations can be emulated using 2D transforms.

Warping

An even more sophisticated method of distorting an image is known as warping.

Conceptually, it is easiest to think of warping as if your image were printed on

a thin sheet of flexible rubber. This rubber sheet can be pushed and pulled by

various amounts in various areas until the desired result is obtained. Image

warping is usually controlled by either a grid mesh or a series of splines. (Spline-

based systems ultimately create a grid as well—they just do a better job of hiding

it from the user.)

Although warping is a powerful tool for manipulating images to obtain effects

that would otherwise be impossible, for illustrative purposes we will use it for a

slightly less serious result. Consider Figure 3.24a, which shows our sample image

with a grid laid over the top. In order to control the warping of this image, we

will manipulate this grid; the corresponding warp will be applied to the image.

Thus, if we stretch our grid as shown in the right half of Figure 3.24b, the resulting

warped image would be similar to that shown in Figure 3.24c. Later, in Chapter

15, we will also touch on the technique of morphing, a sophisticated combination

of warping and dissolving between two images over a period of time.

Expression Language

Just as we saw with the color-correction tools, the ideal compositing system will

allow you to resort to mathematical expressions to define warping parameters.

The syntax will follow the same format as we defined for our color-correction

example, only now we will be dealing with X and Y transformations. The degener-

ate case, in which we are merely mimicking something simple like an X translation,

could be represented as

X ⳱ X Ⳮ 30

The primary difference is that the perspective may not be exactly the same. A good 3D transform

will let you choose a true 3D position, which will in turn affect the resulting perspective of the image.

Basic Image Manipulation 59

(a)

Figure 3.24 Warping. (a) Sample image with grid laid over it.

This transformation would shift every pixel to the right by 30 pixels.

More complex equations can easily be extrapolated. For instance, using a peri-

odic function like sine, we can create a wavy offset:

Y ⳱ Y Ⳮ 50 ⳯ sin(X ⳯ 0.02)

In this example, the sine function returns a value between ⳮ1 and 1 depending

on the value of X. The multiplication by 50 magnifies the effect so that pixels are

offset in the range of ⳮ50 to 50. (Multiplying X by 0.02 before passing it to the

sine function will control the frequency of the wave.) The result of this warp

operation is shown in Figure 3.25.

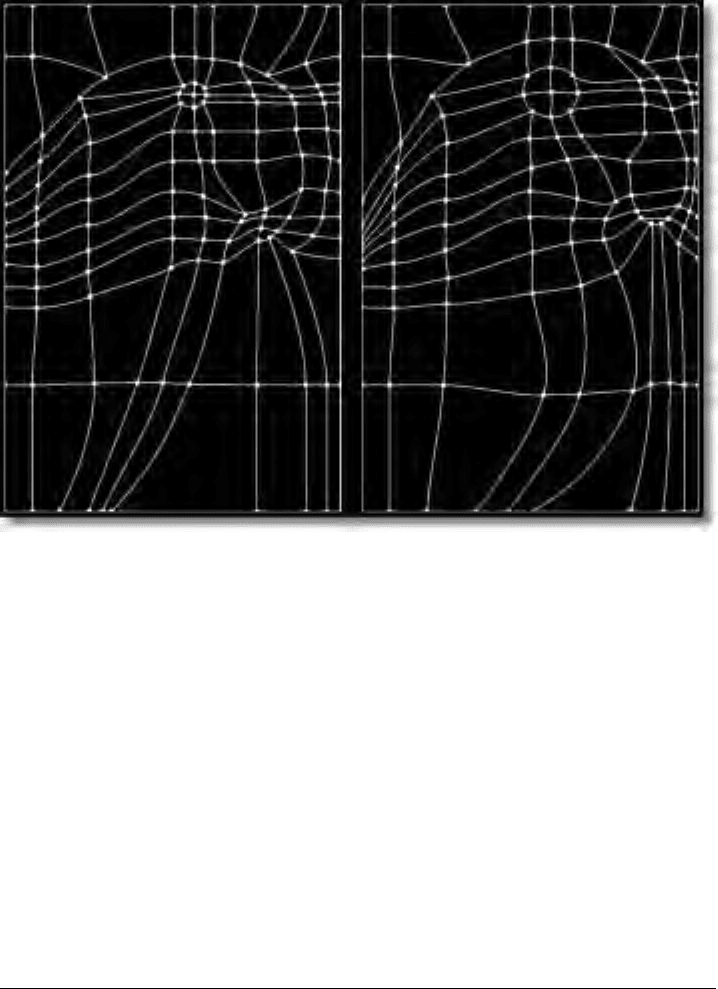
60 The Art and Science of Digital Compositing

(b)

Figure 3.24 (b) Grid before and after distortion.

Filtering Algorithms

Every time a geometric transformation is applied to an image, there is a step in

which the computer samples the original image and creates a new one. Within

this step, there is a choice of what type of filter will be used to produce the new

image.

Consider the situation in which we want to scale an image down to one-

tenth its original resolution. There are a number of ways that we could go about

this. We could simply use every tenth pixel, for instance. This technique is a very

simple filter, generally known as an impulse filter. It is a very fast method of

reducing an image, but unfortunately not a very good one, since it completely

ignores 90% of the data that makes up the original image. Consider the worst-

case example of how this can be undesirable. If pixel number 1 and pixel number

From a mathematical point of view, these filters are essentially the same as the spatial filters that

we have already described. However, their implementation here is different, and the compositing

artist will use them differently.

Basic Image Manipulation 61

(c)

Figure 3.24 (c) Resulting distorted image.

10 in the image are black, but pixels 2 to 9 are white, our scaled-down image

would use a black pixel to represent the new pixel number 1, even though the

average value should be closer to white. Better filtering algorithms look at all of

the pixels in the original image and selectively average these pixels together to

obtain a new pixel that more accurately reflects the data in the original image.

Choosing a specific filter is not just something that we do when scaling an

image down (or up). Every geometric transformation (from a rotation to a warp)

will use some kind of filter to compute the resulting image. Presumably, your

compositing system will allow you to choose a specific filter for most geometric

transformations. (If it doesn’t, it is probably time to get a new compositing system.)

Advanced systems may give you a variety of different filters to choose from by