Braun J., van der Beek P., Batt G. Quantitative Thermochronology: Numerical Methods for the Interpretation of Thermochronological Data
Подождите немного. Документ загружается.


108 Steady-state two-dimensional heat transport
Assuming that the perturbation to the flat-Earth solution is in phase with (i.e. has
the same shape as) the periodic surface topography, it may be written as
T
′
x z = cos
2x
Zz (6.8)
where Zz describes the vertical variation of the perturbation. By substitution
into (6.7), one obtains
2
Z
z
2
+
˙
E
Z
z
−
2
2
Z = 0 (6.9)
which can be used to determine the shape of Zz. On applying standard methods
for solving a second-order partial differential equation, one obtains for Zz
Zz = c
1
e
m
1
z
+c
2
e
m
2
z
(6.10)
This general solution can be verified by simply substituting it into the differential
equation (6.9). Combining this solution with the horizontal part of the solution
(i.e. cos2x/), the flat-Earth solution and the boundary conditions leads to
(Mancktelow and Grasemann, 1997):
Tx z = T
L
1−e
−z
˙
E/
1−e
−L
˙
E/
+ cos
2x
e
−mz
(6.11)
where
=
˙
ET
L
1−e
−
˙
EL/
z
0
m =
1
2
˙
E
+
!
˙
E
2
+
4
2
(6.12)
This solution is shown in Figure 6.2 for three values of the exhumation rate.
The relationships illustrated show the following key features:
• finite exhumation leads to a higher temperature gradient near the surface; this is the
result of heat transport by advection as described in Chapter 5;
• at any given depth, exhumation dampens the amplitude of the thermal disturbance
caused by finite-amplitude topography; and
• at any given temperature, the disturbance increases with exhumation rate.
Indirectly, the last two features result from the advection of the temperature
field, and thus the thermal disturbance caused by the finite-amplitude topography,
towards the surface.

6.1 The effect of surface topography 109
λ = 10 km & z
0
= 2 km &
E = 1.5 km Myr
–1
λ = 10 km &
z
0
= 2 km &
E = 0.5 km Myr
–1
λ = 10 km &
z
0
= 2 km &
E = 0 km Myr
–1
Depth (km)
0
2
4
6
8
10
Depth (km)
0
2
4
6
8
10
0
60
120
180
240
300
360
Horizontal Distance (km)
0 5 10 15 20
Depth (km)
0
2
4
6
8
10
Fig. 6.2. Computed temperature fields showing the dependence of the thermal
perturbation caused by finite topography on exhumation rate; the penetration
depth of the disturbance is inversely proportional to the exhumation rate. The
three panels correspond to Pe =0 05 and 1.5, respectively. Note that, in contrast
to Figure 6.1, the horizontal and vertical scales are the same in all three panels.
Another approximate solution
The above solution (6.11) is not very accurate in the vicinity of the surface.
Consequently, it cannot be used in practice to investigate the distribution of ages
for low-temperature thermochronometers, since these are strongly influenced by
the effects of the surface topography and the conductive transport of heat near

110 Steady-state two-dimensional heat transport
the surface. Another approximate solution that is more accurate has been derived
(Stüwe et al., 1994), but, because it is expressed as an infinite series, it is more
difficult to compute.
The solution is given by
Z = X +X Y (6.13)
in which Z is the dimensionless depth Z = z/L of a chosen isotherm (where z is
the depth positive downwards from the lowest point of the topography). is the
scale of the topography, =z
0
/L. X describes the depth–temperature relationship
in the eroding region without topography and is given by
X =−
1
Pe
ln
1−1 −e
−Pe
(6.14)
in which is the dimensionless temperature =T/T
L
and Pe =
˙
EL/.
X Y describes the perturbation of the isotherms calculated by use of X as
a function of the topography and is given by
X Y = fY +
n=1
n
0
e
−z
fY −
n
−2fY
dz (6.15)
in which
=
sinhPe1 −X/2
sinhPe/2
n
=
−1
n+1
n sin
n1−X
n
2
2
+Pe/2
2
n
z =
z
n
2
2
+Pe/2
2
(6.16)
and Y is the dimensionless lateral distance Y = x/L. fY is the normalised
topography, which can be chosen to be of any shape but should be much smaller
in vertical and lateral extent than L. The integral must be estimated numerically,
for example by using a Gauss Laguerrian quadrature (Abramowitz and Stegun,
1970).
6.2 The age–elevation relationship – steady state
In tectonically active regions characterised by a finite-amplitude relief it is com-
mon practice to collect samples for thermochronological analysis along a ‘vertical
profile’ or locally restricted range of elevations. Because they experience differ-
ent exhumation paths and thus cooling histories, samples collected at the bot-
toms of valleys commonly record ages different from those of samples collected

6.2 The age–elevation relationship – steady state 111
near the adjacent ridge tops. As we will show now, when performed properly,
this sampling strategy is likely to provide good information on the exhumation
rate.
If we consider the limited case of a thermochronological system that is charac-
terised by a very high closure temperature, such that the finite-amplitude topog-
raphy has only a negligible effect on the geometry of the corresponding isotherm,
then one can readily see, as shown in Figure 6.3(a), that the slope of the rela-
tionship between age and elevation is a direct measure of the exhumation rate
(Wagner and Reimer, 1972; Wagner et al., 1977; Fitzgerald and Gleadow, 1988;
Fitzgerald et al., 1995). This is true if total exhumation has been sufficient to
bring rocks to the surface both at the ridge tops and at valley bottoms that have
crossed the closure-temperature isotherm during the same, current tectonic event,
at a fixed exhumation rate,
˙
E (cf. Section 1.2). If the exhumation rate has changed
during this time interval, it will result in a break in slope in the age–elevation
relationship that can be used to date the time of change in the tectonic and/or
erosional regime (cf. Section 1.2).
For a thermochronological system characterised by a low closure tempera-
ture, the corresponding isotherm is likely to be affected by the surface relief.
If, as shown in Figure 6.3(b), the isotherm is disturbed by an amount z
0
,
where z
0
is the amplitude of the surface topography, then the slope of the age–
elevation relationship is
˙
E/1 −, and it provides an overestimate of the real
exhumation rate. Because the steady-state (i.e. at thermal equilibrium) geome-
try of isotherms beneath a finite-amplitude periodic topography is approximately
known (see Equation (6.11)), one can determine a correction factor with which
to extract exhumation rates from age–elevation datasets for low-temperature sys-
tems. For fission-track ages (closure temperature of ∼115
C), the true exhumation
rate
˙
E
T
is related to the apparent exhumation rate (or slope of the age–elevation
relationship),
˙
E
A
, by the following relationship:
˙
E
T
=
˙
E
A
z
z
0
(6.17)
where z is the difference in depth to the closure-temperature isotherm beneath
ridges and valleys. For the fission-track system, one can derive the following
empirical relationship (Stüwe et al., 1994) between z and the exhumation rate:
z = ae
−
˙
E/b
(6.18)
where a and b are constants that depend mildly on the wavelength and amplitude
of relief (see Stüwe et al. (1994) for approximate values of and expressions for a
and b).

112 Steady-state two-dimensional heat transport
d
βz
0
/2
β
z
0
/2
1
2
(c) Low-
T
c
thermochronometry + Relief change
α z
0
/2
Age, a
Elevation, h
E
.
.
a = d/E
T
= T
c
d
h/da =Dh/Da = βz
0
/(
a
1
–
a
2
)
a
1
=
a + z
0
(β – α)/2/
E
.
a
2
=
a – z
0
(β – α)/2/
E
.
hence, d
h/da = βE /(β – α)
.
d
z
0
/2
1
2
(a) High-
T
c
thermochronometry
Age, a
Elevation, h
.
E
.
a = d/E
T
= T
c
d
h/da =Dh/Da = z
0
/(
a
1
–
a
2
)
..
a
1
=
a + z
0
/2/
E & a
2
=a –
z
0
/2/
E
.
hence, d
h/da = E
z
0
/2
d
z
0
/2
1
2
(b) Low-
T
c
thermochronometry
α z
0
/2
Age, a
Elevation,
h
E
.
.
a = d/E
T
= T
c
d
h/da =Dh/Da = z
0
/(
a
1
–
a
2
)
.
a
1
=
a + z
0
(1 – α)/2/
E
.
a
2
=
a – z
0
(1 – α)/2/
E
.
hence, d
h/da = E/(1 – α)
z
0
/2
Fig. 6.3. Age–elevation relationships for (a) high-temperature systems, (b) low-
temperature systems and (c) including the effect of a varying surface relief. After
Braun (2002b). Reproduced with permission from Elsevier.

6.3 Relief change 113
6.3 Relief change
During periods of active tectonics, rock uplift leads to vertical movements of the
surface which, in turn, is reshaped by geomorphic processes. It is therefore likely
that, while rocks are advected towards the surface by denudation, the shape of
the surface is actively changing. Because most geomorphic processes are related
to the movement of water and/or solid rock downslope, the positions of large-
scale geomorphic features (valleys and ridges) are relatively stable. It is their
scale, more precisely the amplitude of the relief, that is likely to change by the
proportionately greatest amount through time. We therefore initially consider the
thermal consequences of a change in relief amplitude only.
If we return to the situation described in Figure 6.3, where rocks are exhumed
at a constant velocity towards the surface, we realise that changing surface relief
amplitude, as depicted in Figure 6.3(c), will perturb the slope of the age–elevation
relationship. Assuming that, between the time the rocks passed through the closure
temperature and the time they are exhumed at the surface, the surface relief has
changed by a factor , one can easily show that the slope of the age–elevation
relationship is given by
a
z
=
˙
E
−
(6.19)
This relationship demonstrates how sensitive age–elevation relationships are to
changes in surface relief. In situations where relief has been substantially reduced
in the relatively recent past < 1, the slope of the age–elevation relationship
becomes steeper with decreasing and can even become negative (if <).
When relief increases > 1, the slope becomes shallower with increasing
and tends towards an asymptotic value (for →) equal to the real exhumation
rate,
˙
E.
Conclusion
Age–elevation relationships contain important information on the tectonic and
geomorphic history of a given region of the crust. It is clear, however, that
caution must be used when one attempts to interpret these relationships. To derive
accurate estimates of the mean exhumation rate from the slope of an age–elevation
relationship, one must apply corrections to take into account the effect of the
finite-amplitude topography on the underlying thermal structure and the effects
caused by recent changes in relief amplitude. However, these corrections require
relatively good knowledge of the evolution through time of the shape of the
surface topography, which, in most cases, is poorly constrained.
114 Steady-state two-dimensional heat transport
Conversely, if one can obtain independent estimates of the mean exhumation
rate, one can regard these perturbations on the slope of the age–elevation relation-
ship as a source of information on the amplitude and rate of change of topography.
This is what we propose to demonstrate in Chapters 7 and 8.
Tutorial 7
Rocks are collected along a transect in a tectonically active area (mean exhumation
rate
˙
E = 12mm yr
−1
) characterised by a finite-amplitude relief (amplitude z
0
=
1km and wavelength = 10 km). The layer being exhumed is 35 km thick and
the temperature at the base of the layer is 400
C. Compute the thermal histories
of three rocks collected (1) at the top of a hill, (2) at mean elevation and (3)
at the bottom of a valley from a temperature of 200
C to the surface. Use
the approximate expression (6.11) to compute the temperature field. Using the
program MadTrax, compute the apparent fission-track ages of the three samples as
well as the apparent exhumation rate derived from the age–elevation relationship.
What can you conclude? Redo the experiment with different wavelengths, = 1
and 30 km; as well as different amplitudes, z
0
= 05 and 2 km. What can you
conclude?

7
General transient solution – the three-dimensional
problem
If one wishes to predict cooling-age estimates following complex
tectonic scenarios (potentially including discrete exhumation episodes)
or in complex situations where a finite-amplitude surface topography
is evolving through time, one cannot use analytical or semi-analytical
solutions or be limited by the assumption of two-dimensionality. In this
chapter, we present a numerical model by means of which to calculate
the solution to the three-dimensional heat-transport equation that is
based on a finite-element method. The code, named Pecube, is made
available to the readers. After a short description of the method used
in Pecube, we use it to solve a problem involving a complex, evolving
surface topography and demonstrate how age datasets can be used to
constrain the rate at which geomorphic processes evolve.
7.1 Pecube
We first recall the expression for the general three-dimensional heat-transport
equation (Section 4.6):
c
T
t
−
˙
E
T
z
=
x
k
T
x
+
y
k
T
y
+
z
k
T
z
+H (7.1)
with the following general boundary conditions:
T
t x y z =Sx y t
= T
S
z
= T
msl
+
r
z −z
msl
Tt x y z =L = T
L
T
n
= 0 along the side boundaries
(7.2)
115

116 General transient solution – the three-dimensional problem
where S describes the geometry of the surface,
r
is the atmospheric temperature
lapse rate and z
msl
and T
msl
are fixed reference height and temperature (at mean
sea level, for example). An initial temperature field is also defined:
Tt = 0xyz= T
0
x y z (7.3)
Note that, in Equation (7.1), we have included only the vertical advection term,
neglecting the potential thermal perturbation caused by lateral heat advection. This
is because lateral temperature gradients are usually much smaller than vertical
ones. In some tectonic situations, lateral heat advection may be important; we
discuss this point in detail in Chapter 10.
Following the steps described in Section 5.3, we have recently developed a
Fortran code called Pecube (Braun, 2003) that, although rather conventional in
its conception, includes a novel approach to the incorporation of a time-varying
surface geometry.
7.2 Time-varying surface topography
The finite-element grid in Pecube is made of vertical triangular or rectangular
prisms (Figure 7.1) that permit any complex surface geometry to be connected
to a flat base (where the fixed-temperature basal boundary condition is imposed).
This geometry implies that nodes are aligned in vertical columns.
To account for the time-varying geometry of the upper surface, a Lagrangian
approach is used, which consists of vertically translating the top nodes of the
mesh by the required amount,
˙
Sx y tt, at the start of each time step. This
method is accurate provided that t < z/10
˙
S, where
˙
S is the rate of change
of the surface topography. The vertical translation of the top nodes may lead
to mesh distortion and an inaccurate solution to the equation. To circumvent
this problem, the temperature field is interpolated from the deformed mesh onto
an ‘undeformed’ mesh at the end of each time step. Because of the nature of
Fig. 7.1. Two types of three-dimensional prismatic elements used in Pecube.
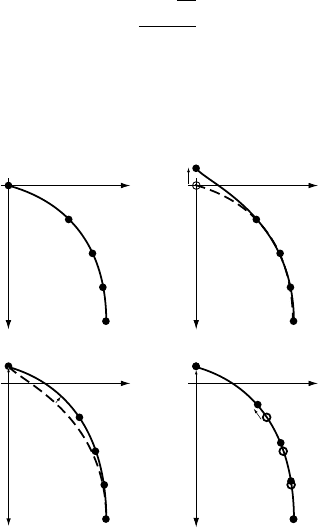
7.2 Time-varying surface topography 117
the finite-element mesh used in Pecube this interpolation needs to be performed
only in the vertical direction, thus minimising potential smoothing errors. The
procedure is illustrated in Figure 7.2.
To improve stability in cases in which heat advection dominates over diffusion,
a streamline-upwind Petrov–Galerkin method is used (Hughes and Brooks, 1982)
and the shape-function matrix, N , in the advection term in the finite-element
equation,
V
e
N
T
˙
EB dV
e
(7.4)
is replaced by
N
∗
= N +
˙
EB
3
(7.5)
where
=
z
√
15
˙
E
(7.6)
and z is a vertical length scale (the thickness of the element).
A complete description of the program Pecube is given in Appendix 8.
T
z
Time-step start
T
z
Surface update
T
z
Conduction
(a)
(c)
T
z
Interpolation
(b)
(d)
Fig. 7.2. In (a) and (b) we illustrate the Lagrangian method used to incorporate
the effects of vertical movement of the upper boundary; (c) shows thermal
relaxation over time step t; and (d) shows interpolation from the ‘deformed’
grid, represented by the open circles, onto a new ‘undeformed’ grid represented
by the black circles.
